通用 博客文章

多物理场仿真和仿真 App 推动创新
2025年 11月 18日
了解为什么您的团队应该考虑将最新版本的 COMSOL Multiphysics® 作为您的研发工作流程的一部分。

你的电阻器性能有多可靠?
2025年 10月 13日
以设计电阻器为例,了解不确定性量化模块中的 4 种研究类型,包括筛选、灵敏度、传播和可靠性。
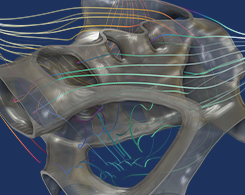
换热器的优化
2025年 6月 25日
由于换热器的设计和制造成本高昂,开发换热器是一项艰巨的任务。探索如何使用形状优化和拓扑优化来提供帮助。

COMSOL Multiphysics® 软件中的人机交互功能
2025年 6月 12日
COMSOL Multiphysics® 6.3 版本引入了 Chatbot 人机交互功能。这篇博客通过几个示例,深入介绍如何使用这项功能为建模仿真过程提供助力。
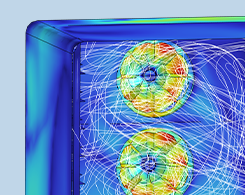
食品安全领域的5 个仿真实例
2025年 5月 7日
2024 年消费者对食品安全的信心降至历史最低点,这使得企业确保其产品安全变得至关重要。了解建模和仿真如何帮助企业确保产品安。

模型求解完成后如何使用作业序列保存数据
2025年 4月 24日
这篇博客可以指导用户如何在求解模型后,自动化常见任务。阅读博客,了解如何使用作业序列功能。

模型求解完成后如何自动导出图像
2025年 4月 23日
你知道 COMSOL Multiphysics® 可以在模型求解完成后自动导出结果图像和动画吗?点击此处,了解详情。

如何导入图像并放样成实体
2025年 3月 21日
假设你想模拟一个不规则的形状,比如人类的头部。如何建立几何图形呢?在这篇博客中,我们将介绍如何通过导入图像和放样实体来实现这一点。
