通用 博客文章
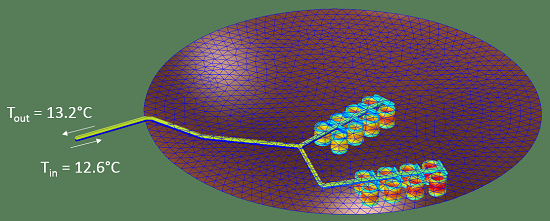
电气设备的对流冷却仿真
在集群计算的帮助下，我们与 BLOCK transformoren 一起对电感器件的对流冷却进行了建模，以获得最佳性能。
使用 COMSOL 理解稳定性方法
在这里，我们提供了一个质量传输示例模型，以帮助描述稳定方法对您的数值模型的影响。
如何在不知道积分限的情况下对函数进行积分？
您知道 COMSOL® 软件可以解决积分和偏微分方程吗？学习如何积分函数——即使不知道积分的极限。
弱形式的力量
如果你正在使用有限元仿真软件（例如 COMSOL Multiphysics），就会在某些时候遇到“弱形式”这一表述。这个时候，你可能会想知道这个表达是什么意思？实际上，弱形式是一个非常强大的概念。
COMSOL Multiphysics® 的几何内核
几何内核 是负责处理 COMSOL Multiphysics® 中几何的软件组件。您或许想要了解它的意义、原理及作用。我们将在下文中进行介绍。
COMSOL Multiphysics 能够求解什么类型的流-固耦合问题?
经常有人问我：“COMSOL Multiphysics 能够求解流-固耦合(FSI)问题吗？”答案当然是肯定的。接下来，我将介绍几种求解流-固耦合问题的方法，以及分析这些不同问题所需要的 COMSOL 产品。 各种类型的流-固耦合模拟 广义上讲，只要模拟过程涉及计算流体中的速度和（或）压力场，以及与流体相互作用的固体材料中的应力和应变，就是在求解流-固耦合(FSI)模型。 圆柱绕流 在模拟流-固耦合问题时，您可以进行各种假设，来降低模拟的复杂度并减小计算量。首先，我们来看一个使用 COMSOL Multiphysics 创建的最完整的流-固耦合模型：绕圆柱的流体流动。 切向流场中一个圆柱体尾流中的柔性物体变形情况。 圆柱体后方的流体尾流引起其后方的突出物产生大幅振荡，求解这类模型需要解决三个问题。首先，在流体流动区域求解纳维-斯托克斯方程。接着，计算固体位移。最后，求解流动域的网格变形问题，以考虑流体可以流经的变形区域。 对于这种非线性多物理场耦合，您可以使用 MEMS 模块 或者结构力学模块中的流-固耦合 接口模拟。这类模拟可以在时域中求解，也可以看作稳态（定常）问题求解。 上述示例考虑了固体材料中应力和应变之间的线性关系。如果想模拟具有非线性应力-应变关系的材料，例如通常用于描述橡胶和聚合物的超弹性材料模型，还需要使用非线性结构材料模块。 蠕动泵:一种利用滚轮在软管上滚动来推动流体流动的泵。 图片来源：Veryst Engineering。 单向流-固耦合 另一种情况，您可能提前知道结构位移相对较小，但应力可能很大。对于这种情况，仍然可以使用 流-固耦合 接口，但也可以使用 单向耦合 求解器计算流动解，并在结构上施加流体载荷。这样，就可以避免计算网格的变形。 您也可以完全不使用流-固耦合接口，重新开始考虑这类单向耦合 FSI 问题，铝挤出工艺中的流-固耦合案例模型就介绍了这种处理方法。此外，如果您正在求解非常高速的流动问题，并且不关心流动中的短时间尺度紊乱振荡，那么可以将湍流流动模型作为流-固耦合模型的一部分。CFD 模块和传热模块中都包含适用于不同流态的各种湍流模型。 周期性流场中的太阳能电池板模型：计算了太阳能电池板周围的湍流气流和由此产生的结构应力。 流体中的结构振动 如果您提前知道正在模拟的是流体中的振动结构，那么通常可以假设结构位移相对较小。因此，在周围流体中诱发的任何体运动都可以忽略。但是，由于结构在振动，流体将产生压力波，从而产生声辐射。我们可以通过 COMSOL 软件中的声学模块所提供的 声-结构相互作用 接口来求解这类问题。 这个接口假定物体位移的变化相对较小，因此不会引起流体产生明显的体运动，只会引起流体压力场的变化。您可以在时域中求解这类问题，也可以假设位移和压力随时间呈正弦变化。这样，就能够在频域中模拟，耗费较小的计算量。在模拟分析过程中，还可以考虑包括由于流体黏度和材料阻尼引起的体损耗。 扬声器辐射的声压级。 此外，您还可以进一步求解热热声-固耦合问题，它求解的是纳维-斯托克斯方程的线性频域形式，还可以考虑显式模拟产生的热和黏性边界层中的损耗。虽然这比声-固耦合问题的计算成本更高，但仍然比求解完整的流固耦合问题更高效。 振动微镜: 振动微镜的应力和位移以及周围空气的速度分布。 多孔弹性介质 声学模块中的 多孔弹性波 接口还可以模拟波在多孔介质（如潮湿的土壤、生物组织和减震泡沫等）中的传播。这个接口可以同时求解结构位移和固体孔隙中流体的压力。例如，计算声波在水-沉积物界面的声反射。 如果您对模拟多孔弹性介质感兴趣，但需要在稳态或时域而不是在频域中求解，那么你需要使用地下水流模块。该模块可以模拟土壤和其他多孔介质中稳态或瞬态压力驱动的流动和静应力。它还包含一个 多孔弹性 接口，用于模拟稳态和瞬态状态下多孔弹性流体和结构的相互作用。 开孔分支井模型: 绘制了土壤中的应力和多孔弹性域中的流体速度。 薄层流体和管道流 上述所有方法都显明确模拟了流体的体积，并求解了这些体积中的速度和（或）压力。在流体层相对较薄的情况下（例如在流体动力轴承中），完全可以不采用整个流体的体积模型，而只求解雷诺方程，获得流体薄膜中的压力。 这种方法只求解沿域边界的流体流动。CFD 模块和MEMS 模块都内置了这个接口。您甚至可以更进一步，只求解沿一条线的流体流动。换句话说，可以使用管道流模块求解沿管道的流动。 对于同时考虑求解沿管道长度的压力变化和管壁弹性影响的模型，请查看这个求解水锤方程的案例模型。 可倾瓦推力轴承:润滑层中的压力场和可倾瓦推力轴承的变形。 进一步简化计算 您可能已经发现，我们是从最复杂的示例开始，逐步探讨如何简化计算，尤其是流体流场的计算。现在，考虑一种极端的情况，即流体完全不移动但确实对结构施加了一个静水压力载荷的示例。 核心功能 对于这种情况，我们可以利用 COMSOL Multiphysics 的核心功能：用户自定义方程、组件耦合算子和全局方程来解决。这些功能允许在模型中引入任意方程，来表示如流体压力等任何变量。正如我们在上一篇博客中所介绍的，您也可以在变形的封闭腔中考虑可压缩和不可压缩流体的影响，以及由此产生的静水压力。 搅拌器模块 我们已经介绍了简化流体流动问题和计算应力的各种方法，接下来，我们考虑已知固体刚体运动的情况下，如何模拟流体运动。对于这种问题，我们可以通过搅拌器模块来求解，即求解搅拌器和搅拌容器的问题。 在这些问题中，固体结构的运动完全由旋转定义，然后再计算流体的运动情况。如果假设固体发生线性弹性变形，还可以计算运动固体中的应力分布。这可以通过单向耦合来解决，即先求解由搅拌器搅拌引起的流体流动，然后在结构变形较小的假设下计算应力。 搅拌器中的流场。 结语 如您所见，COMSOL Multiphysics 能够处理各种类型的流-固耦合模拟问题。如果您对文中的内容感兴趣，或者文中介绍的内容没有涉及您所关注的问题，请联系我们。
建立贝奥武夫集群加速多物理场仿真
很多人都需要最新的软件和硬件来提升工作效率，因此，我们要紧跟科技发展的步伐。但如何处理过时的硬件呢？将它们报废或是扔在角落，这都显得有点浪费。其实我们可以利用这些废旧硬件来组建一个贝奥武夫集群，以提升计算速度与生产率。
如何充分利用网络浮动许可证（FNL）？
从安装角度来看，COMSOL 单机许可证（CPU）和网络浮动许可证（FNL）的主要区别在于它们的安装和管理方式。FNL 不仅包含单机许可证的所有功能，还提供多个附加功能，能够大大改进您的工作流程，推动 COMSOL Multiphysics 随着贵公司的发展而不断扩展运用。
借助 COMSOL API for use with Java® 实现建模任务的自动化操作
如今新产品的研发周期越来越短，为了在市场竞争中抢占先机，研发工程师和科学家们需要一件高效的工具，来帮助他们最快地获取计算结果，并摆脱重复性的例行工作。COMSOL Multiphysics® 正是他们需要的！COMSOL 软件拥有参数化扫描等多种内置功能，可帮助用户提高仿真工作效率。除了能够实现图形建模之外，它还拥有应用编程接口（Application Programming Interface，简称 API）。借助 API，用户便能对任意重复的建模步骤实现自动化操作。下面我们来了解一下 COMSOL API for use with Java®。
批处理扫描中任务并行的附加值
到目前为止，我们在混合建模系列博客中还没有详细讨论的一件事是，当向我们的计算中增加更多计算资源时，我们可以期待怎样程度的加速。今天，我们考虑一些解释并行计算局限性的理论研究，并将介绍如何使用 COMSOL 软件的批处理扫描 选项。这是一个内置的、易并行计算功能，可在达到极限时提高性能。 Amdahl 定律和 Gustafson-Barsis 定律 我们之前已经提到过的如何通过增加计算单元来提高速度是基于算法的（在这篇文章中我们将使用术语进程，但添加的计算单元也可以是线程 ）。一个严格的串行算法，像计算Fibonacci 数列的元素，完全不能从增加过程中受益，而并行算法，如向量加法，可以利用与向量中的元素一样多的处理器。实际中的大多数算法都介于这两者之间。 为了分析一个算法可能的最大加速，我们将假设它由一小部分完全并行化的代码和一小部分严格串行化的代码组成。我们调用并行代码 \varphi 的分数，其中，\varphi 是介于(包括) 0 和 1 之间的一个数字。这自动意味着我们的算法有一个等于 (1-\varphi) 的串行代码片段。 考虑 P 个活动进程的计算时间 T(P)，从 P=1 开始，我们可以使用表达式 T(1) = T(1) \cdot(\varphi + (1-\varphi))。当运行 P 个进程时，代码的串行部分不受影响，但完全并行化的代码的计算速度将提高P倍。因此，P 进程的计算时间为 T(P)=T(1) \cdot (\varphi / P + (1 -\varphi))，加速度为 S(P):=T(1)/T(P)=1/(\varphi/P+(1-\varphi))。 Amdahl 定律 这个表达式是Amdahl 定律的核心。对于不同的值 \varphi 和 P 绘制图 S(P) ，我们现在在下图中看到一些有趣的东西。 为可并行化代码的不同部分增加进程数的加速比。 对于 100% 并行化代码，极限是不存在的。然而，我们发现对于 \varphi<1，渐近极限或理论最大加速比为 S{max}(\varphi):=\lim{P\to \infty} S(P)=1/(1-\varphi)。 对于 95% 并行化的代码，我们发现 S{max}(0.95)=20，即使我们有无限数量的进程，最大加速也是 20 倍。此外，我们有 S{max}(0.9)=10, S{max}(0.75)=4 和 S{max}(0.5)=2。当减少并行化代码的比例时，理论最大加速比会迅速下降。 但不要现在就放弃回家! Gustafson-Barsis 定律 Amdahl 定律没有 考虑到一件事，那就是当我们购买一台速度更快、内存更大的计算机来运行更多进程时，通常不是想更快地计算之前的小模型。相反，我们想要计算新的、更大（更酷）的模型。这就是 Gustafson-Barsis 定律的全部内容。它基于这样一个假设，即我们要计算的问题的规模随着可用进程的数量线性增加。 Amdahl 定律假定问题的大小是固定的。当添加新的处理器时，它们处理的是最初由较少数量的进程处理的部分问题。通过添加越来越多的进程，我们并没有充分利用所添加进程的全部能力，因为最终它们能够处理的问题大小达到了下限。然而，假设问题的大小随着添加的进程数量的增加而增加，那么我们就将所有进程利用到假设的水平，并且执行计算的加速是无限的。 描述这种现象的方程是 S(P)=\phi\cdot P-(1-\phi)，这为我们提供了一个更为乐观的结果，即所谓的缩放加速（类似于生产力），如下图所示： 当考虑到工作的规模通常会随着可用进程的数量而增加时，我们的预测就更加乐观了。 通信成本 Gustafson-Barsis 定律意味着，我们拥有的能添加到进程中的资源才能限制我们可以计算的问题的大小。然而，还有其他因素会影响加速。到目前为止，我们在这个系列博客中试图强调的一点是，通信成本较高。但是我们还没有谈到它有多贵，所以让我们看一些例子。 […]
混合计算：共享内存与分布式内存相结合的优势
在之前的混合计算系列博客中，我的同事 Pär 介绍了如何在共享内存和分布式内存平台上使用 COMSOL Multiphysics 进行并行数值模拟。今天，我将讨论这两种方法的结合：混合计算。
绘制磁场的空间导数
对于放射学、磁电泳、粒子加速器和地球物理学等领域的应用，计算磁场或磁通量密度的空间导数都很有用。