在最新版本的 COMSOL® 软件中,您可以在半导体模块中使用新的薛定谔方程 接口进行建模。今天这篇博文,让我们来看一个简单的示例模型,这个模型使用了此接口来估计超晶格结构的电子和空穴基态能级。通过构建类似的模型,器件工程师能够计算给定周期结构的带隙并调整设计参数,直到达到所需的带隙值。
编者注:此博文于 2020 年 1 月 23 日更新,反映了软件最新的功能和信息。
超晶格结构的有效带隙
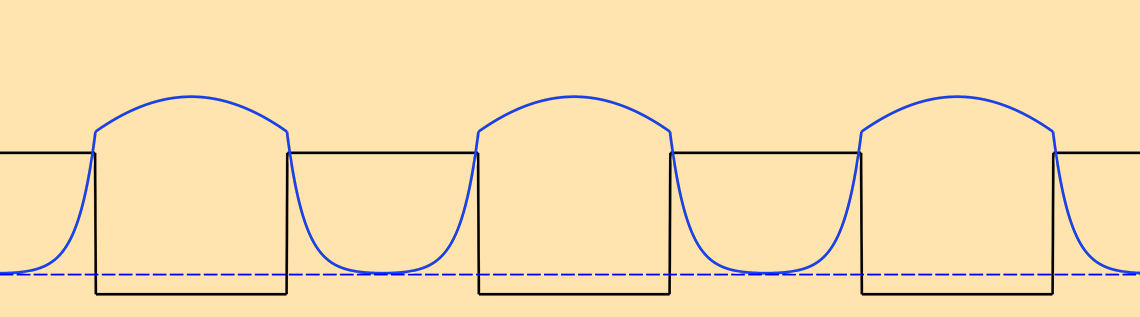
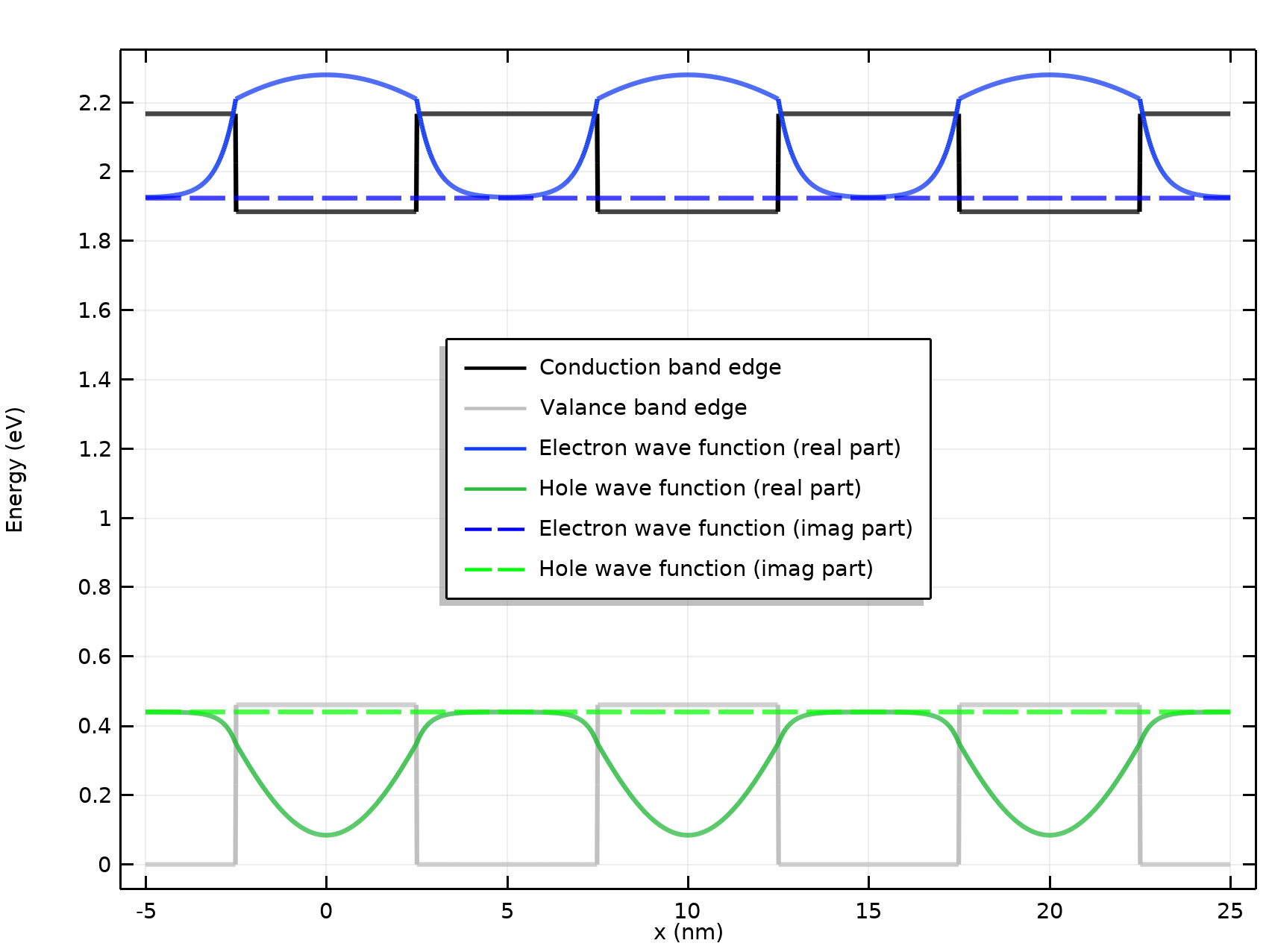
由于量子限制效应,超晶格结构的有效带隙比体阱材料中的有效带隙更宽——电子和空穴大多被限制在阱中,其基态能量从带边缘偏移。下面显示了一个示例,其中黑色和灰色线表示导带和价带边缘,蓝色和绿色曲线分别表示电子和空穴波函数被基态能量偏移。
COMSOL Multiphysics® 模型
这个模型简单明了,易于理解。使用了两个 薛定谔方程 接口:一个用于电子,另一个用于空穴。在每个接口下,两个 电子势能 节点用于设置方波形带边缘,同样,两个 有效质量 节点用于设置阱区和势垒区的有效质量。模型中只需要包含一个超晶格结构的晶胞,端点应用 周期性条件 边界条件。
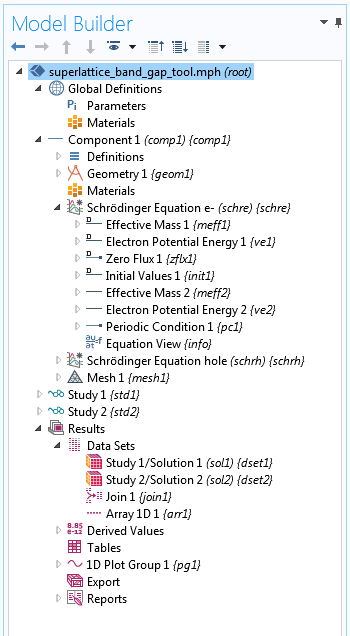
COMSOL 模型开发器树结构。
在两个特征值研究中分别求解电子和空穴的基态能量。使用 数组 一维数据集将结果从一个晶胞扩展到三个晶胞 ,这也是 COMSOL Multiphysics® 软件的新增功能。
关于 薛定谔方程 接口
在物理场接口的设置面板中有一些参数值得注意。
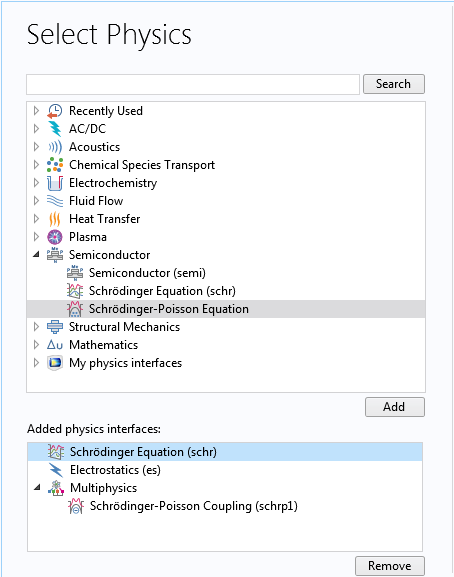
薛定谔方程接口的设置面板。
特征值尺度
一个重要的参数是特征值尺度 λscale (单位: J)。这个参数用于特征值研究,将无单位的特征值相对于特征能量进行缩放。例如,默认值 1eV 允许特征值的数值以 eV 为单位呈现特征能量的值。因此,1.924 的特征值(如下面的屏幕截图所示)对应于 1.924eV 的特征能量。
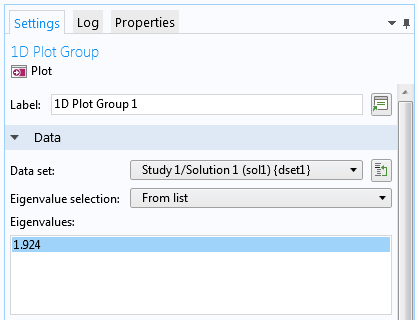
特征值研究的设置。
如果将特征值比例设置为 1meV,那么相同的特征值将对应于 1.924 meV 的特征能量(来自不同模型的结果)。
能量
另一个参数是能量E(单位:J),用于稳态研究以指定稳态薛定谔方程的总能量。
薛定谔方程接口中的符号约定
时谐因子
在物理场接口中执行的单分量薛定谔方程如下:
{r},t)}{2\, m_{eff}(\mathbf{r})}\right) + V(\mathbf{r},t)\Psi(\mathbf{r},t) = -i \hbar \frac{\partial}{\partial t}\Psi(\mathbf{r},t)
请注意,方程右侧的能量算子采用了与大多数量子力学教科书采用的符号相反的约定。这是因为 COMSOL Multiphysics 对时谐解采用了exp(+iωt) 的工程惯例来约定 ,而不是 exp(–iωt) 的物理学约定。薛定谔方程 接口采用工程约定,因此 COMSOL® 系列产品中的符号约定保持一致。在这种不寻常的符号约定下,动量算子也获得了相反的符号——因为平面波现在是 exp(–ikx + iωt),而不是 exp(+ikx – iωt),就像大多数教科书一样。
电子势能
电子势能 域条件的符号约定遵循半导体 接口采用 的符号约定 。对于类电子粒子,能量较低的方向是电子势能的负方向。从图像上看,这种类型的粒子倾向于落到电子势能阱的底部。对于类空穴粒子,能量较低的方向是电子势能的正方向。这种类型的粒子在图形上倾向于漂浮到电子势能峰的顶部。
使用薛定谔方程接口建模的另一个例子
双势垒一维 基准模型也使用了 薛定谔方程 接口。它包括应用这个物理场接口的多种不同方式,例如:
- 准束缚态的特征值研究
- 准束缚态衰减的瞬态研究
- 特征值研究求解共振隧穿条件,其中 100% 传输发生在经典禁止区域 – 一种奇特的纯量子力学效应
- 稳态研究求解作为能量函数的传输和反射系数,显示以共振隧穿能量为中心的窄传输峰值
对于这个模型,使用 开放边界 边界条件允许波函数泄漏出建模域而不会反射回来。这个边界条件还有一个可选的入射波特征和一个 用于共振隧穿条件的入射类型 的高级物理场选项 ,其中 100% 的波函数被添加到建模域中而不会反射回来。
希望您能了解这个新物理场接口的更多应用,包括解决一般量子力学问题以及量子阱、线和点。
更多资源
- 在发布亮点中详细了解 COMSOL® 软件新版本中半导体模块的新功能
- 在 COMSOL 博客上浏览更多半导体仿真示例:



评论 (2)
显安 刘
2023-10-27刘老师 方便给一个邮件吗 有一个问题一直搞不出来
hao huang
2023-10-30 COMSOL 员工您好,你可以描述一下您的问题或者发送相关模型至技术支持邮箱:support@comsol.com