
本博客是弱公式化系列博客的后续部分。在之前的博客中,我们使用 COMSOL Multiphysics 软件设置并求解了一个典型的弱形式方程,并借助一些简单的物理参数验证了结果。今天我们将深入了解这些方程是如何被离散并数值求解的。
简单示例
请回想之前稳态无热源的一维传热示例,其中温度 T 是定义在区间 1\le x\le 5 求解域中的关于位置 x 的函数。边界条件:左边界 (x=1) 处向外通量为2,右边界 (x=5) 温度为 9,弱形式方程表达式:
(1)
现在尝试对方程进行数值求解。
基础函数
如要数值求解方程 (1),首先需将域 1\le x\le 5 平均分成四个子区间或网格单元,通过五个节点 x = 1, 2, \cdots, 5 隔开。然后可以定义一组基函数或形函数,\psi_{1L}(x), \psi_{1R}(x), \psi_{2L}(x), \psi_{2R}(x), \cdots, \psi_{4R}(x), 如下图所示,每个网格单元内都有两个形函数,分别由实线和虚线表示。
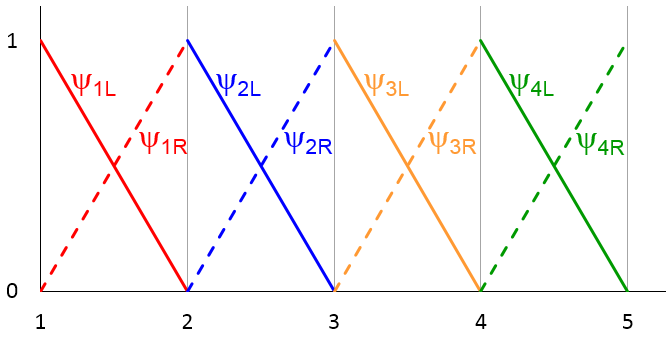
例如,在第一个单元 (1 \le x \le 2) 中,有如下关系
(2)
\psi_{1L}(x) %26=%26 \left\{ \begin{array}{ll}
2-x \mbox{ for } 1 \le x \le 2,\\
0 \mbox{ elsewhere}
\end{array} \right \mbox{ (solid red line)}
\end{equation}
\psi_{1R}(x) %26=%26 \left\{ \begin{array}{ll}
x-1 \mbox{ for } 1 \le x \le 2, \\
0 \mbox{ elsewhere}
\end{array} \right \mbox{ (dashed red line)}
\end{equation}
我们观察到每一个网格单元中的形函数都是范围从 0 到 1 的简单线性函数,函数在网格单元外消失。
注意: COMSOL 支持由高阶多项式组成的形函数,而非只是线性函数。此处选择线性形函数是为了视觉上更直观。
使用这一组形函数,我们可以通过一个简单的线性组合来近似 1\le x\le 5 域内的任意函数:
(3)
其中 a_{1L}, a_{1R}, a_{2L}, a_{2R}, \cdots 为对应每一个形状函数的常系数。下图中以黑色曲线表示任意函数 u(x)。蓝绿色曲线表示由形函数 (3) 叠加得到的近似值。方程 (3) 右侧的每一项都使用相同的颜色和线条样式表示。
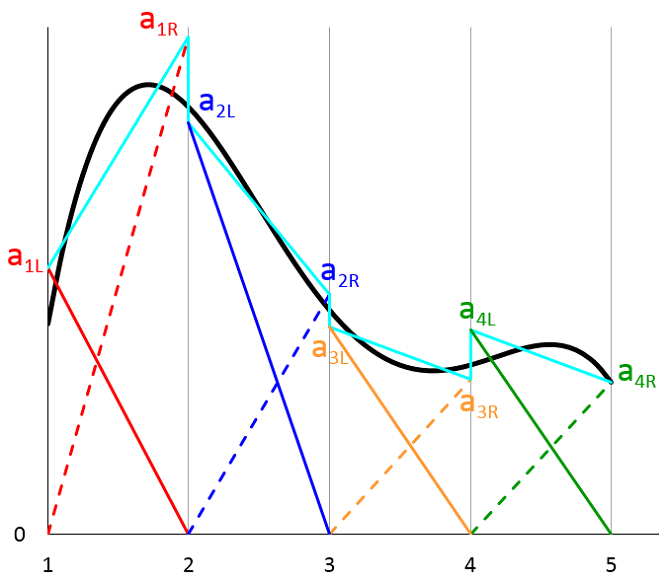
总体来看,近似曲线(由蓝绿色曲线表示)在相邻网格单元的边界处可以不连续。在实际条件下,许多物理系统,包括我们的简单传热示例,都应得到连续解。因此,大多数物理场接口的缺省形函数都是拉格朗日单元,其形状函数系数都是受约束的,以便能在相邻网格单元的边界处得到连续解。在该示例中,我们对近似曲线进行了简化,如下图所示:
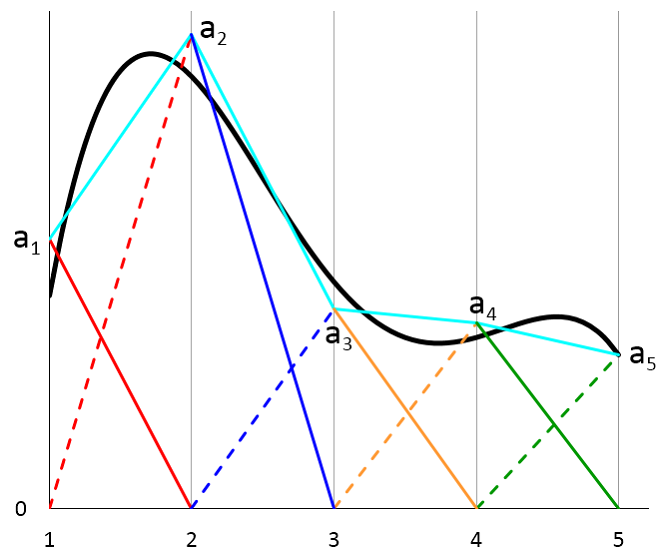
其中蓝绿色曲线由于设定每一个网格边界处的系数相等:a_{1R} = a_{2L}, a_{2R} = a_{3L}, a_{3R} = a_{4L}. 简便起见,我们重命名了系数:
\begin{align}
a_1 %26\equiv a_{1L}\\
a_2 %26\equiv a_{1R} = a_{2L}\\
a_3 %26\equiv a_{2R} = a_{3L}\\
a_4 %26\equiv a_{3R} = a_{4L}\\
a_5 %26\equiv a_{4R}
\end{align}
\end{equation*}
我们看到为实现表达式 (3) 中的连续性条件,要求每个形函数对使用相同的系数。现在可通过把这些形函数对组合成一组新的基函数 ϕ1(x),ϕ2(x),⋯,ϕ5(x) 进行简化,并使每个函数受限于一个节点:
(4)
\begin{align}
\phi_1(x) \equiv \psi_{1L}(x) %26= \left\{ \begin{array}{ll}
2-x \mbox{ for } 1\:$\leq$\:\textit{x}\:$\leq$\:2,\\
0 \mbox{ elsewhere}
\end{array} \right
\\
\phi_2(x) \equiv \psi_{1R}(x) + \psi_{2L}(x) %26= \left\{ \begin{array}{lll}
x-1 \mbox{ for } 1\:$\leq$\:\textit{x}\:$\leq$\:2, \\
3-x \mbox{ for } 2\:\textless\:x\:$\leq$\:3, \\
0 \mbox{ elsewhere}
\end{array} \right
\\
\phi_3(x) \equiv \psi_{2R}(x) + \psi_{3L}(x) %26= \left\{ \begin{array}{lll}
x-2 \mbox{ for } 2\:$\leq$\:\textit{x}\:$\leq$\:3, \\
4-x \mbox{ for } 3\:\textless\:x\:$\leq$\:4, \\
0 \mbox{ elsewhere}
\end{array} \right
\\
\\ \cdot
\\ \cdot
\\ \cdot
\end{equation*}
如下图所示,每一个新的基函数都为呈三角形、以某一节点为中心的分段线性函数。其在节点附近网格单元内的值域为 1 到 0,在其他地方消失。
如上文中所讨论的,选择这组新的基函数后,我们将解限制为在相邻网格单元边界处连续。大多数物理系统都能满足该连续性限制,包括我们的简单传热示例。
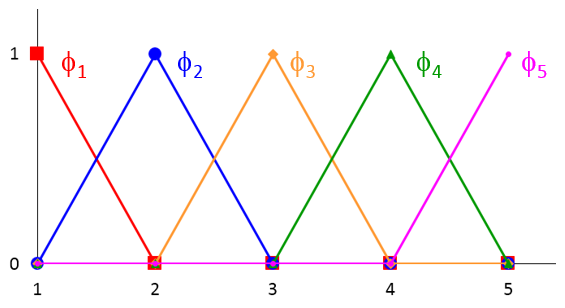
现在结合这组新的基函数,近似表达式 (3) 被简化为
(5)
下图中,任意函数 u(x) 由黑色曲线表示。青色曲线表示由叠加新基函数得到的近似。方程 (5) 右侧的每一项都使用如上图相同的颜色和线条样式表示。
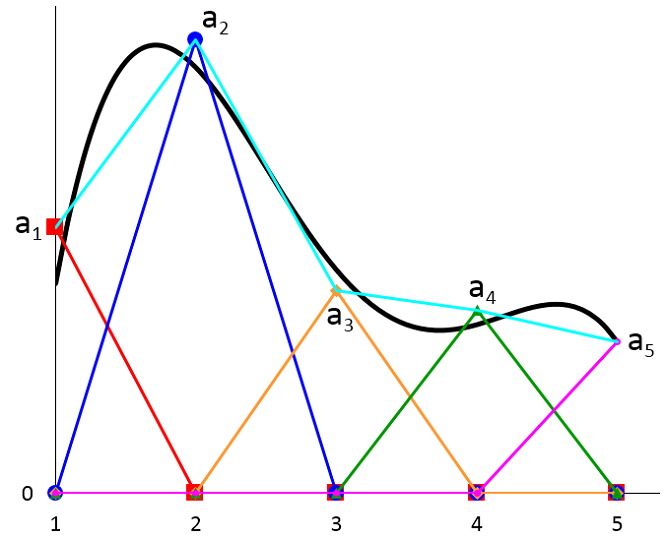
题外话,如果黑色曲线表示某些真实建模问题的精确解,那么我们看到近似并不是很好,这是因为粗化网格的关系。而且并不要求结点值 a_1, a_2, \cdots 依赖于精确解,除非受限于已知解的值(以上图的 a_5 为例)。黑色和蓝绿色曲线之间的偏差表示解的离散误差。在二维和三维模型中也会存在几何的离散误差。我的同事 Walter Frei 所写的“线性静态问题的网格剖分注意事项”博客着重讨论了两类误差。由于存在此类潜在误差,“执行网格细化研究”以确保建模结果的准确将十分必要。
我们注意到方程 (5) 给出的近似曲线(蓝绿色曲线)是一个分段线性函数。因此无法对其二阶导数进行数值求解。我们之前提到过,弱形式能对方程组内的导数降阶从而简化计算。在该案例中,只需要一阶导数即可轻松得到数值解。在之后的博客中,我们将讨论一个材料属性中的不连续性示例,求导降阶也能为其带来计算优势。
两步离散弱形式方程
结合上述的新基函数组,我们将通过两步对弱形式方程 (1) 进行离散。首先,温度函数 T(x) 可由方程 (5) 中相同的方法利用基函数组近似:
(6)
其中 a_1, a_2, \cdots , a_5 是待定的未知系数。
将 T(x) 的表达式 (6) 代入弱形式方程 (1) 可得到:
(7)
a_1 \int_1^5 \partial_x \phi_1(x) \partial_x \tilde{T}(x) \,dx + a_2 \int_1^5 \partial_x \phi_2(x) \partial_x \tilde{T}(x) \,dx + \cdots + a_5 \int_1^5 \partial_x \phi_5(x) \partial_x \tilde{T}(x) \,dx
\\
= -2 \tilde{T}_1 -\lambda_2 \tilde{T}_2 -\tilde{\lambda}_2 (a_5 -9)
\end{array}
其中,对于右边界 x=5 处的温度 T_2,可使用表达式 (6) 及基函数受限进行计算,得到一项 a_5 \phi_5(x=5) = a_5,对 T(x=5) 产生贡献。
我们看到弱形式方程 (7) 的离散形式中有六项未知数:五项系数 a_1, a_2, \cdots , a_5 以及右边界的通量 \lambda_2。 习惯上将未知数称为自由度。此处,我们可以说,(离散化)问题包含“六个自由度”。
要求解该六项未知数,我们需要六个方程。这就进入离散化的第二步。回忆 第一篇博客中对试函数的介绍,它的功能在于对方程进行局部采样以对域内每一处的解进行限制。现在我们已经有一组局部函数,即基函数 \phi_1, \cdots, \phi_5,所以我们可将其代入方程 (7) 中的试函数 \tilde{T} 得到所需的六个方程。
下表展示了将产生六个方程的六个代入项:
| \tilde{T}(x) | \tilde{\lambda}_2 |
|---|---|
| \phi_1(x) | 0 |
| \phi_2(x) | 0 |
| \phi_3(x) | 0 |
| \phi_4(x) | 0 |
| \phi_5(x) | 0 |
| 0 | 1 |
因为每一个基函数都为局部函数,每一个代入将得到包含较少项的方程。例如第一次代入将得到:
a_1 \int_1^5 \partial_x \phi_1(x) \partial_x \phi_1(x) \,dx + a_2 \int_1^5 \partial_x \phi_2(x) \partial_x \phi_1(x) \,dx + \cdots + a_5 \int_1^5 \partial_x \phi_5(x) \partial_x \phi_1(x) \,dx
\\
= -2 \phi_1(x=1) -\lambda_2 \phi_1(x=5) -0 (a_5 -9)
\end{array}
注意到 \phi_1 只对其自身和 \phi_2 存在显著交叠。因此只有左侧的前两项非零。而且 \phi_1 受限于左边界 (x=1),所以右侧只剩下第一项。方程现在变成:
(8)
我们已对左侧的定积分求值:
\begin{align}
\int_1^5 \partial_x \phi_1(x) \partial_x \phi_1(x) \,dx %26= 1\\
\int_1^5 \partial_x \phi_2(x) \partial_x \phi_1(x) \,dx %26= -1\\
\end{align}
\end{equation*}
并在右侧使用 \phi_1 的定义:\phi_1(x=1) = 1.
类似地,剩下的五次代入将产生下述方程:
(9)
\begin{align}
-a_1 + 2 a_2 -a_3 %26= 0\\
-a_2 + 2 a_3 -a_4 %26= 0\\
-a_3 + 2 a_4 -a_5 %26= 0\\
-a_4 + a_5 %26= -\lambda_2\\
0 %26= -(a_5 -9)\\
\end{align}
\end{equation*}
我们现在拥有关于六项未知数的六个方程,可以直接验证出解与之前博客中使用 COMSOL Multiphysics 软件得到的结果匹配。例如最后一个方程直接给出 a_5 = 9,使用温度表达式 (6) 得到其在右边界的值:
\begin{align}
T(x=5) %26= a_1 \phi_1(x=5) + a_2 \phi_2(x=5) + \cdots + a_5 \phi_5(x=5)\\
%26= a_1 \cdot 0 + a_2 \cdot 0 + \cdots + a_5 \cdot 1\\
%26= 9\\
\begin{align}
\end{equation*}
结果符合右边界温度为 9 的固定边界条件。同样可以轻松发现正是与试函数 \tilde{\lambda}_2 相关的项推出了方程 (0 = a_5 -9),与预期一致。
矩阵表示
可以简便地将离散方程组系统(我们的简单示例包含由 (8) 和 (9) 给出的六个方程)写成矩阵和矢量的形式:
(10)
\begin{array}{cccccc}
1 & -1 & 0 & 0 & 0 & 0 \\
-1 & 2 & -1 & 0 & 0 & 0 \\
0 & -1 & 2 & -1 & 0 & 0 \\
0 & 0 & -1 & 2 & -1 & 0 \\
0 & 0 & 0 & -1 & 1 & 1 \\
0 & 0 & 0 & 0 & 1 & 0
\end{array}
\right)
\left(
\begin{array}{c} a_1 \\ a_2 \\ a_3 \\ a_4 \\ a_5 \\ \lambda_2 \end{array}
\right)
= \left(
\begin{array}{c} -2 \\ 0 \\ 0 \\ 0 \\ 0 \\ 9 \end{array}
\right)
当将该技巧用于结构力学应用时,左侧的矩阵通常被称作刚度矩阵,右侧的矢量常被称为载荷矢量。
我们注意到矩阵方程有两个很有意思的地方。首先,矩阵中有许多 0(所谓的稀疏矩阵)。实际模型中的网格单元会远多于示例中的四个网格单元,我们可以预见到矩阵中的大部分单元都是 0。这为选择局部形函数带来了直接便利,因此是一个高效的方程系统数值求解方法。
其次,拉格朗日乘子 \lambda_2 只出现在一个方程中(矩阵的最后一列只有一个非零单元)。剩下的五个方程只涉及五个未知系数 a_1, a_2, \cdots , a_5。因此,我们可以选择使用五个方程来求解 a_1, a_2, \cdots , a_5,而无需求解 \lambda_2。在 之前的博客中也曾简要提过,总体来说,可以选择不求解拉格朗日乘子以得到更高的计算速度。
总结和弱形式系列的下一主题
今天,我们回顾了在简单传热示例中对弱形式方程进行离散的基本过程。我们在两个步骤中用到了一组局部形函数:
- 以它们为基准来近似真实解
- 逐个将它们代入弱形式方程得到离散方程组系统
最终得到稀疏的矩阵方程,可用电脑对其快速求解。
在之前的博客中,当我们使用 COMSOL Multiphysics 执行弱形式方程时,离散化在软件内部完成,无需用户操作。接下来,我们将向您展示如何使用软件中的弱解型偏微分方程接口检查刚度矩阵和载荷矢量,以及是否需要求解拉格朗日乘子。



评论 (6)
Kai Li
2021-04-01为什么我看不到方程(4)
hao huang
2021-04-02 COMSOL 员工感谢您的提醒,公式(4)已正常显示。
Kai Li
2021-04-02矩阵表示那里
{结果符合右边界温度为 9 的固定边界条件。样可以轻松发现正是与试函数 相关的项推出了方程 (),与预期一致。}
少了个字,应该是“同样”
hao huang
2021-04-02 COMSOL 员工感谢提醒,文字已修改。
Zhengyu Shi
2023-06-13请问下 lambda2 的试函数 选为 1 ,是如何选择的呢?
Kaixi Tang
2023-06-25 COMSOL 员工你好,lambda2可以理解为使得让x=5处的狄式边界满足的拉格朗日乘子。所以lambda2在x=5处等于1,其实就隐含了在x=5处的狄式边界条件得到了精确满足。