在解决化学物质传递问题时，我们常常会处理具有高佩克莱特数的情况，其中对流与扩散之比非常高。我们还可能需要处理结构沿流动方向呈周期性且流场本身呈周期性的问题。这时，我们就可以通过使用 COMSOL Multiphysics 中的广义拉伸组件耦合和前一步解算子来大大减少此类问题的计算需求。
周期性微流体设备的多物理场建模
我最近写了一篇关于利用周期性在微流控设备模型中重复使用流动解的博客文章。如下图所示，微流体设备可能具有小的蛇形通道。通过两个入口向同一溶剂中引入了不同的溶质，并期望在出口处得到良好的混合。
一个典型的微流控设备。图片源自 IX-factory STK 。在CC BY-SA 3.0下获得许可，通过Wikimedia Commons共享。
我们知道，可以仅在一个重复元胞单元中计算流体流场，并沿着重复结构对该流动解进行构图，以定义整个设备中的流场。然后可以在重复的部分中计算稀物质传递 问题，如下图所示。
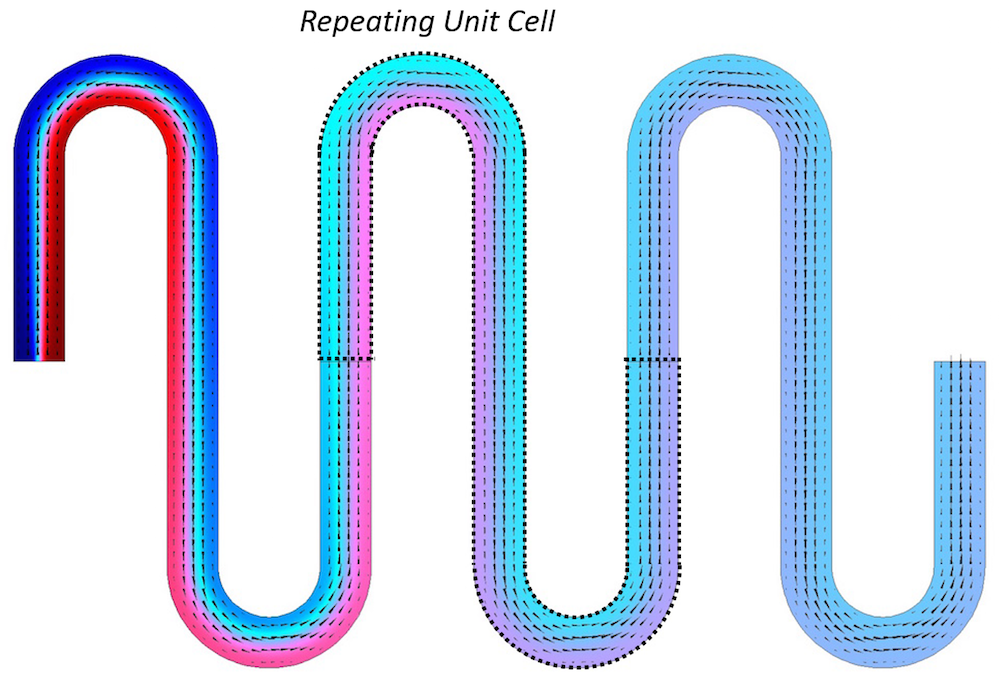
一种方法是计算一个子单元中的流场。该流动解可用于解决整个域内的化学物质传递问题。
在完成该主题的博客文章后不久，我的一位同事向我提出了挑战，他提出了一种模拟这种情况的更简单的方法，这使我想到了以下问题。
从上面的图像中可能无法立即看出，这种情况下的佩克莱特数非常高，这意味着由于流体的运动而引起的物质传递远大于通过扩散进行的物质传递。换句话说，下游解不会影响上游解。
如果佩克莱特数很高，那么我们不必对整个域上的稀物质传递问题 进行求解。我们可以在用于计算流体流场的同一基本单元上求解它，但我们需要想出一种方法将输出边界处的物质分布映射回输入边界，然后重新运行仿真。让我们看看如何做到这一点。
广义拉伸算子，边界方程，前一步解和参数扫描
下图概述了我们应遵循的建模过程。我们可以将整个建模域减少到一个基本单元。我们将使用层流流入和流出条件来计算此基本单元中的流场。计算出的流场将用于 稀物质传递 接口中的传递项，另外入口处还需要定义浓度分布。
我们可以从假设入口处的特定物质浓度开始，并在整个建模域中求解浓度场。然后，评估出口处的浓度分布；将该分布映射回入口边界，并将该入口边界用作新的入口条件；再次求解模型。每次重复此过程时，我们实际上是在求解我们的微流控设备下一个（下游）基本单元中的浓度分布。
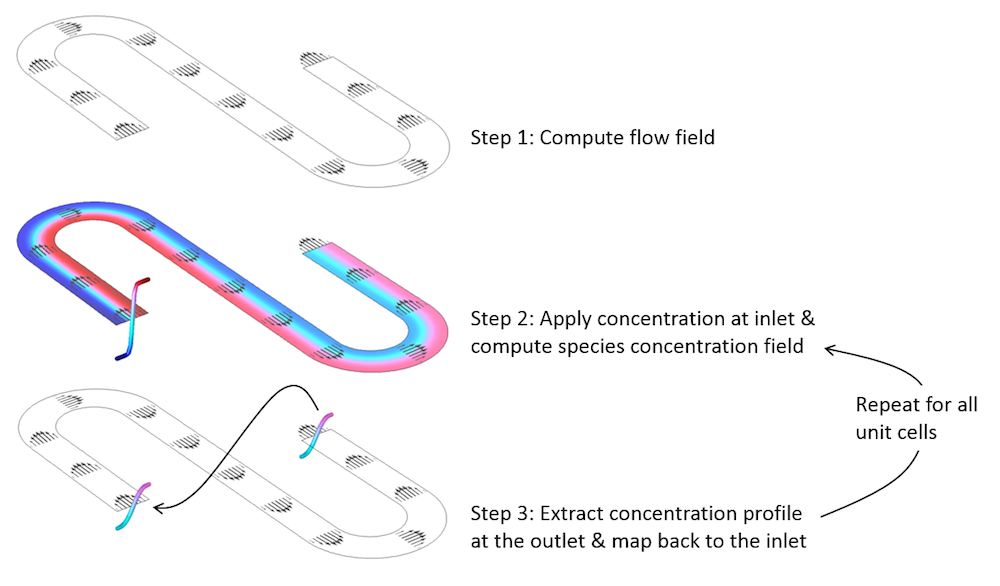
用一个简单基本单元对重复微流体设备进行建模的求解过程。
建模实现开始于在出口边界定义一个名为 genext1 的广义拉伸组件耦合。通过指定沿 x 轴的位移，这种耦合简单地将出口边界处的场映射回入口边界，该方法类似于之前博客文章中的方法。
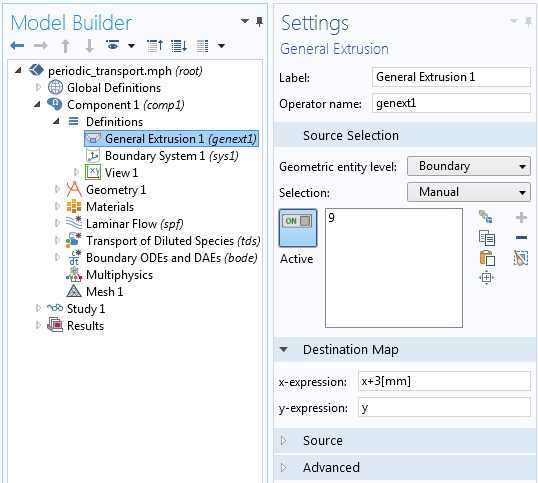
使用拉伸组件耦合通过一个 3mm 的指定偏移将一个边界上的解映射到另一个边界。
接下来，将边界常微分和微分代数方程 接口添加到入口边界。该接口的设置如下图所示。该变量名为 c_b，并且离散化被设置为拉格朗日—线性 以匹配稀物质传递 接口的离散化。分布式常微分方程 的源项 为 (c_b-genext1(c))[m^3/mol]，它将入口处 c_b 的值设置为 c。在出口处计算物质浓度，然后通过广义拉伸算子映射回入口。
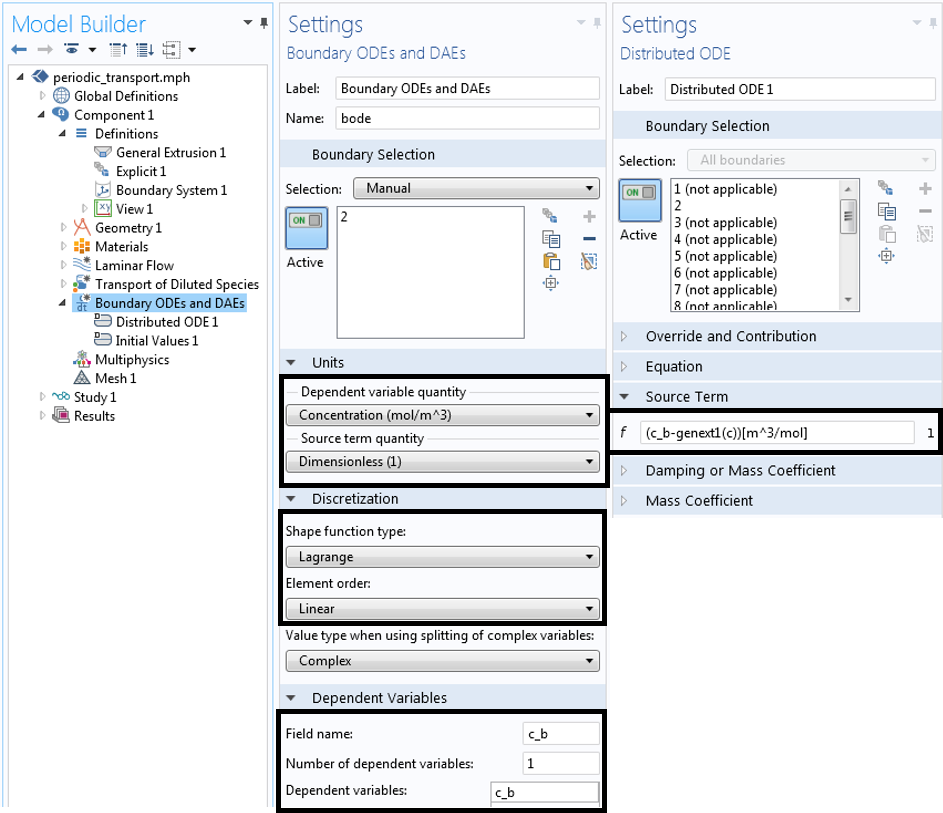
边界常微分和微分代数方程接口。图中突出显示了相关设置。
接下来，我们看看在哪里使用变量 c_b。下面的屏幕截图显示了稀物质传递 接口的流入边界条件。
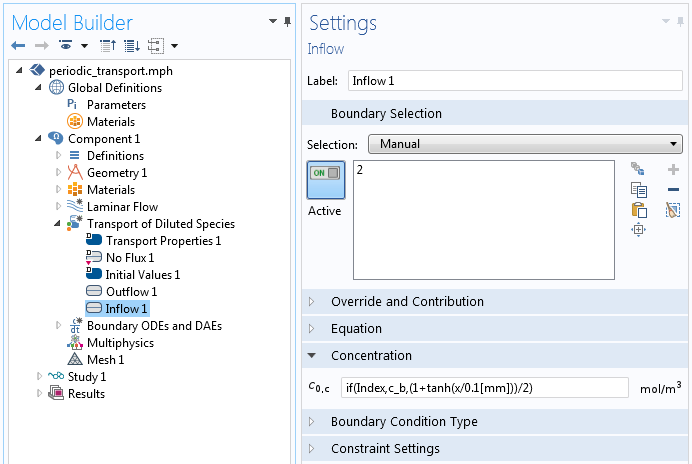
稀物质传递接口的入口条件。
输入的表达式为 if(Index,c_b,(1+tanh(x/0.1[mm]))/2)，该表达式使用 if() 语句根据全局参数 Index 设置不同的入口浓度。表达式 (1+tanh(x/0.1[mm]))/2 是设备入口处的假定物质浓度（该浓度被设置为从 0 到 1 范围内的值），并且仅当 Index 等于零时适用。对于任何其他 Index 值，入口处的物质浓度实际上取自出口处计算的物质浓度。
但是，我们如何指定，希望将前一步计算的出口浓度用作当前的入口浓度？为此，我们需要修改研究设置。该研究 由两个连续的稳态步骤 组成。第一步仅解决层流 接口。产生的稳态流体速度场将自动传递到第二步，该研究步同时求解稀物质传递 以及边界常微分和微分代数方程 接口。
如下面的屏幕截图所示，第二个稳态步骤 包括一个辅助扫描。请注意，指数 参数的值为 0、1 和 2，它们代表了我们要模拟的系统的三个基本单元。还要注意，将运行继续计算 设置为无参数 （因为在这种情况下使用负载斜坡或非线性斜坡没有好处），并且将重用上一步的解 设置为是。
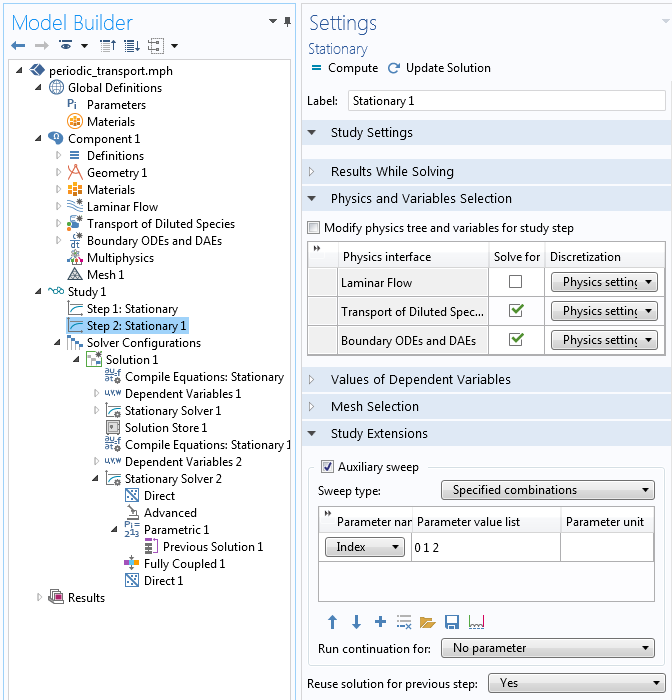
启用辅助扫描的稳态研究步骤。
我们还需要对求解器配置 进行另一项修改。需要手动将前一步解 节点添加到参数 节点，并指定应在参数扫描的上一步中访问变量 c_b。相关设置如下图所示。
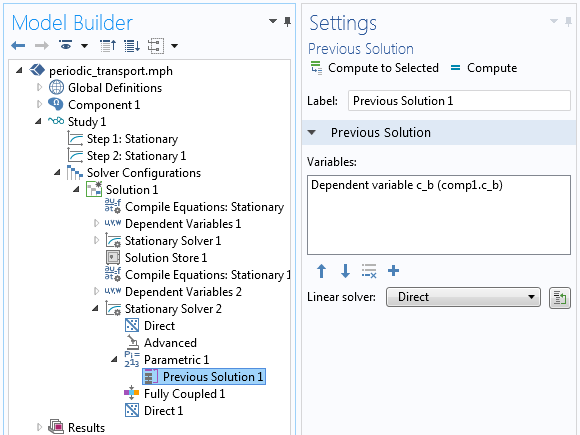
在前一步解节点设置。
在这些研究设置下，我们对三个基本单元中的每一个基本单元进行重复仿真，并在计算浓度场之前将浓度场从出口传递回入口。我们可以将结果合并为单个绘图来显示整个目标域中的浓度分布。
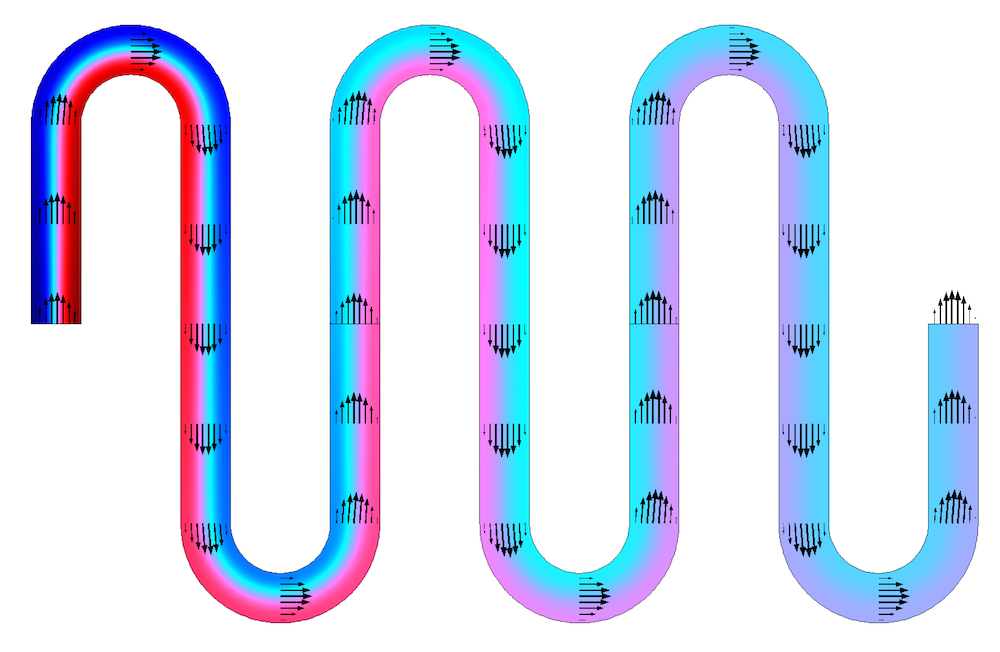
使用高佩克莱特数依次求解三个基本单元绘制得到的浓度场。
关于模拟高佩克莱特数的周期性结构的概述
本博客文章中显示的方法适用于高佩克莱特数周期性结构中化学物质传输的模型。该过程对于解决 COMSOL Multiphysics 中其他以传递为主的问题当然也是有效的。即使我们在此假设流动是周期性的并且流体的属性是不变的，也可以将该方法扩展为将流场从出口映射回入口。
这里显示的问题也可以通过 LiveLink™ for MATLAB® 来解决，它为我们提供了一个脚本接口，使我们能够提取数据、重新映射，并使用不同的输入重新运行解。不过，我们也很高兴可以在图形用户界面（GUI）中构建此类模型。
这里的计算优势将随着我们必须分析的基本单元的数量而增长。如果有 N 个基本单元，则使用此方法的内存要求和求解时间将比构建整个模型小约 N 倍。
如果您对此有疑问，并且有兴趣使用 COMSOL Multiphysics 来满足您的建模需求，请联系我们。
评论 (0)