
从事流体流动研究的工程技术人员对有限元法是否适用于 CFD 仿真一直存在争议,其中一些工程技术人员坚定地认为,有限体积法比有限元法更具优越性。这个观点有科学依据吗?我们不能一概而论,不同的方法可能适用于不同的问题,我们来看一下具体原因。
科学、技术和传统
有限元法被数值分析界广泛用于研究流体流动的数值方法。在相关科学出版物中,有大量关于 CFD 和有限元法的描述,以及节点间断伽辽金(DG)法的最新研究,后者是一种采用不连续基函数的有限元法。
用于 CFD 仿真的商业软件包传统上基于有限体积法,这是因为基本上所有大型 CFD 商业软件包的来源都相同。业界对有限体积法投入了大量的精力和技术。现在,业界采用多种方法来高效、准确地计算结构化(例如六面体,即块体)和非结构化(例如四面体)网格的通量并进行积分。
也就是说,对于流体流动问题而言,有限体积法优于有限元法这一假设没有任何理论或实践支持。首先,存在许多不同的有限体积法和有限元法,其中一些方法在某些方面是相同的;其次,方法的实现对软件的实际使用有很大的影响。我们可以说,对于某些特定的问题,软件包 X 似乎比软件包 Y 更适用。不过,这并不是因为其中一个软件使用了有限元法,而另一个使用了有限体积法。下面我们来解释一下其中的原因。
有限元法 vs. 有限体积法:哪个最好?
数学模型和数值模型
我们先来看一个通用的数学模型:
(1)
(2)
u = f{\text{ 初始条件}} \hfill
\end{gathered} $
Bu = g{\text{ 边界条件}} \hfill
\end{gathered} $
其中, P表示微分算子,u 表示因变量(解变量),F 表示源,f 是描述初始条件的函数,B 是一个算子,g 是边界上的函数。在本例中,空间坐标 \mathbf{x} 表示所有三个方向(x, y, 和 z )。
数学模型可以描述流体流动等物理现象。在这种情况下,模型可以表示空间和时间中动量和质量的守恒。幸运的是,源于这种守恒定律的数学模型加上初始值和适当的边界条件后往往运行良好。这意味着存在唯一解,该解在问题取多个数据(例如,初始值、源项或边界条件)的情况下始终成立。
尽管一个问题存在唯一且稳定的解,但很难或者说几乎不可能解析化的找到这样的解,也就是说,可能很难找到用便于计算的算子(+、-、x、÷)描述的解析表达式。那么我们必须建立一个接近数学模型的数值模型,然后使用可在计算机程序中实现的数值方法 来求解数值模型方程。
有限元法和有限体积法是基于模型方程空间离散化的数值方法。对于常微分方程,时间离散化通常采用某种时间步格式来实现,上面定义的数学模型给出了如下数值模型:
(3)
(4)
{u_h} = {f_h}{\text{ 初始条件}} \hfill
\end{gathered} $
{B_h}{u_h}= {g_h}{\text{ 边界条件}} \hfill
\end{gathered} $
其中,h 表示离散化参数,比如有限元法或有限体积法中的网格单元或单元大小。
请注意,网格中的构建块在有限元法中称为element,在有限体积法中称为cell。
误差有多个源。截断误差$\tau $ 可以帮助我们辨别数值模型与数学模型的近似程度:
(5)
数值模型的 精确度 揭示截断误差随着h 的减小而减小的速度。这意味着单元大小越小,数值模型与数学模型之间的差异就应该越小。如果截断误差随h 减小,则数值模型是一致的。
解的离散化误差 为模型方程的精确解与数值解之差:
(6)
如果数值解随着h减小而接近精确解,则可以认为数值方法收敛:
(7)
离散化的精确度 p 揭示数值解随着 h 减小收敛为精确解的速度。
(8)
{h^p}
$
p 值越大,近似值收敛得越快。
那么,有限元法与有限体积法在精确度上有什么内在的区别吗?通过增加基函数的阶数,理论上我们可以用有限元法达到任意精确度(在实践中,还有其他限制因素)。最常见的有限元法是二阶至三阶精度,而有限体积法是一阶至二阶精度。
两者有哪些相同点和不同点呢?
我们来看一个通量平衡方程,它是流体流动数学模型的基础:
(9)
{\partial t}
+ \nabla \cdot \Gamma = F{\text{ 在}}\Omega内
在这个方程中,u 表示守恒物理量,如动量或质量,\Gamma 表示该量的通量,比如单位面积和单位时间内流过控制面的动量。
有限元法首先建立一个积分方程,方程用试函数 \varphi 加权,然后通过对模型域进行积分来求平均值:
(10)
{\nabla \cdot \Gamma } \right)\varphi dV} = \int\limits_\Omega {F\varphi dV} $
不过,在继续之前,我们要对{\Gamma \varphi } 应用散度定理,从而得出如下表达式:
(11)
其中,\partial \Omega 表示域 \Omega 的边界, \mathbf{n} 表示域边界的法矢。对上述方程左边部分求积分得出:
(12)
这意味着,根据 方程 11,我们可以得到:
(13)
{\nabla \cdot \Gamma } \right)\varphi dV + } \int\limits_\Omega {\Gamma \cdot \nabla \varphi dV} = \int\limits_{\partial \Omega } {\left( {\Gamma \varphi } \right) \cdot {\mathbf{n}}dS}
从而得出如下表达式:
(14)
\right)\varphi dV} = -\int\limits_\Omega {\Gamma \cdot \nabla \varphi dV} + \int\limits_{\partial \Omega } {\left(
{\Gamma \varphi }
\right) \cdot {\mathbf{n}}dS}
我们可以将上面的方程 14 代入方程 10 的第二项,这样做是为了在积分方程中自然地包含通量边界条件,这种做法在随后的数值实现过程中带来好处,即通量矢量不必是可微分的,进而得出有限元法中的基础方程:
(15)
这就是所谓的弱形式。左边的第三项对u 、\Gamma 在域\partial \Omega 边界上的通量进行积分。如果弱形式对大量的试函数\varphi 都成立,则它只与物理模型有关。常见的一种选择是使用多项式,但也可以是其他类型的函数。一个特例是常数试函数;例如,\varphi = 1。上面最后一个方程方程 15 变为:
(16)
这个关系式是有限体积法的基础。
至此,有限元法与有限体积法没有区别。如上所述,有限体积法的公式 方程 16 只是有限元法中使用的一般弱形式 方程 15 的特例。不同之处在于 方程 15 和 方程 16 的离散化。有限元法的依据是,选取有限数量的测试函数\varphi = \varphi_h,并要求 方程 15 对所有函数都成立。有限体积法的依据是,选取有限数量的控制体积\Omega = \Omega_h ,并要求 方程 16 对所有控制体积都成立。如果我们使用三角剖分法作为这两种方法的基础,图 1 和图 2 分别显示了有限元和有限体积公式可能的离散形式。
我们观察最常见的有限元法会发现,试函数仅在节点(局部支持函数)附近是非零的,这意味着只需对这附近的element(这里是三角形)计算积分,比如下面图 1 中突出显示的域节点及其附近的灰色element。边界通量的贡献( 方程 15 左边第三项)只需包含在边界上有面(三维)或边(二维)的element中,这是因为,element间边界贡献抵消了连续基函数。下面的图 1 显示了如何为域中的内部element(白色、灰色和绿色)以及边界上有面(三维)或边(二维)的element(浅蓝色)建立方程。对于图 1 域中突出显示的节点,只有周围的灰色element对(\Omega 域上)域积分有贡献。对于边界上突出显示的节点,只有两个相邻的浅蓝色element对\partial \Omega 域上的积分有边界通量贡献,而这两个浅蓝色element和浅绿色element对(\Omega 域上)域积分都有贡献。
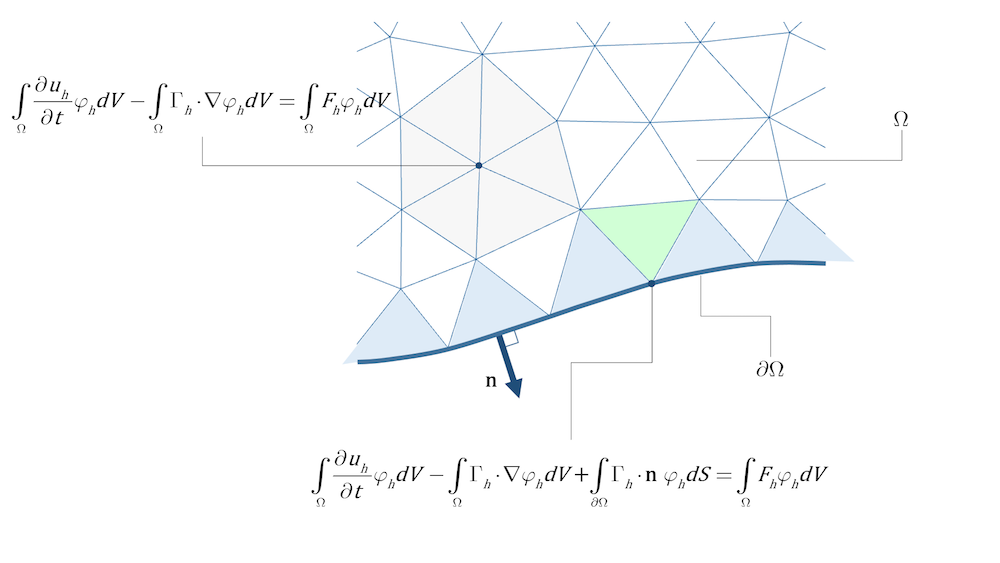
图 1. 内部element(白色和灰色)和边界上有面(三维)或边(二维)的element的域贡献。灰色六边形中间节点的基函数在所有周围element中(即在所有灰色element中)都有支持;边界处节点的基函数在浅蓝色element中有支持,在边界处有节点的任何element(如浅绿色element)中也有支持;通量的积分仅从边界上有边的element(浅蓝色element)获得贡献。
离散通量的域表达式\Gamma_h 根据通量的本构关系得出,对流扩散方程(流体流动方程中的扩散项是动量传递的粘性项)就是一个例子。 方程 15 中通量的边界表达式根据特定模型的边界条件得出,然后,我们将这些表达式作为对上面图 1 中边界单元(浅蓝色)的贡献。
我们再观察常见的有限体积法,即cell中心法,会发现每个cell(三角形)都被视为一个单独的域。通量的边界项(方程 16 左边第二项)对所有cell(包括内部cell和边界上有面(三维)或边(二维)的cell)进行积分。通量的本构关系用于域的面或边,而边界条件用于边界上的面或边;参见下面的图 2。
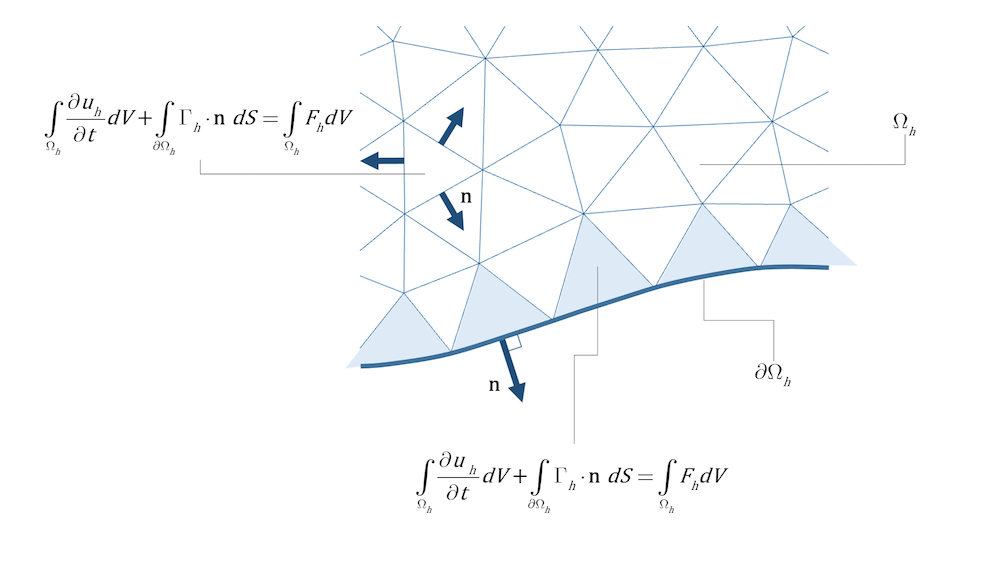
图 2. 对所有cell面(三维)或边(二维)(包括内部cell和边界上有面或边的cell)上的通量求积分。
那么我们如何用两种不同的方法来表达 u 和\Gamma 呢?
有限元法通常采用与试函数相同的基函数来近似求解。只要解的近似值有一个次数大于零的多项式,并且一阶导数可以近似导出,就不需要特别处理对流和扩散产生的通量。通量矢量也是一个局部多项式函数。
相反,在有限体积法离散化中,边界上的解没有很好地定义。该方法仅为每个cell定义解的值,通常解释为cell中心的值。因此,有限体积法需要通过某种重建方法来完成。通常,在考虑相邻cell值的情况下,使用局部插值方法;见图 3 中的示例。为了得到解和通量的高阶插值,需要考虑更多的cell值,这不仅非常复杂,而且会导致更少局部的方法。
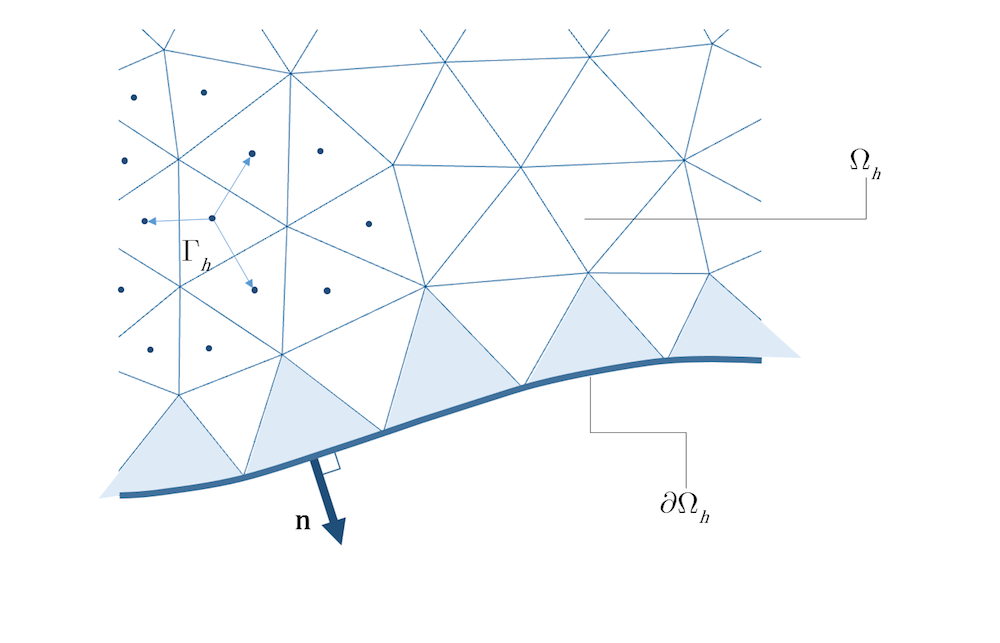
图 3. 在以cell为中心的有限体积法中,通量矢量通过在以cell为中心的点之间插值来构建。
根据有限元法中采用的基函数和有限体积法中采用的通量构建类型,我们可以实现不同的精度。采用二阶精度法的粗化网格比采用一阶精度法的细化网格得到的解更精确。
有限元法的线性试函数和基函数通常需要采用二阶精度的方法。有限元法在离散化方面有较大的灵活性。例如,使用二次基函数相当简单,也不需要对解进行重建或插值。该方法本质上是非常对称的,边界上的通量边界条件可以通过自然、直接的方式施加。
有限元法的一个缺点是,对于连续试函数和基函数,没有局部守恒性,只能保证全局守恒。换句话说,只能保证域边界上的净通量是平衡的。另一个缺点是无法控制局部通量,这意味着稳定对流占主导地位的流动的离散化并不简单。在这种情况下,稳定意味着消除离散化产生的非物理振荡。对流占主导地位的流动的局部守恒和稳定性问题都可以通过直接或间接修改试函数,也就是修改弱形式来解决。不过,这些方法的计算量可能非常大。
如上文所述,有限体积法对应于分段常数有限元基函数,可能对通量采用高阶插值方案,这需要采用一阶或二阶精度方法。有限体积法的局部表述可以实现局部守恒,这是该方法极具吸引力的一个特征。这意味着每个cell的净通量都保证是平衡的,进而能够以自然、直接的方法来稳定对流占主导的流动问题的离散化。通过修改cell间边界上的通量可以自然地实现所谓的逆风稳定和其他稳定。逆风在对流通量方向的离散化中产生非对称性。
有限元法的好处是能够为不同阶数的基函数制定方法。高阶基函数给出了高阶、精确的方法,这有助于提高给定网格的精度。有限体积法采用零阶基函数,但可以对通量使用高阶插值方案,这也提高了精度。当使用高阶方法时,得到的系统变得更大,相同网格的求解时间增加,不过,精度也更高。因此,我们在比较性能时,必须在给定的精度条件下进行比较。用不同的方法以相同的精度测量解决流体流动问题所需的 CPU 时间和内存是比较不同方法性能的正确方式,而不是比较cell或element的数量。
有限元法的前景
COMSOL 软件主要采用有限元法解决 CFD 问题,这是我们的专长所在。在过去的 15 年中,研发团队在研究采用不连续试函数和基函数的有限元法方面取得了重大成就,也就是引言中提到的 DG 方法,这些方法中的试函数对于每个element来说都是局部的,弱形式的方程适用于每个element。局部守恒是自动实现的,高阶离散化非常简单,也不需要重建解,但零阶方法除外,零阶方法相当于有限体积法。此外,element边界上的局部通量是公式的自然组成部分,这意味着很容易实现稳定性。DG 方法的一个缺点是引入了相对大量的额外自由度,这就需要研究混合 DG 方法,在这种方法中,离散化更为精简,自由度更少。
关于有限元法和有限体积法的总结性思考
正如本文所述,有限体积法和有限元法都有各自的优缺点。要对大规模流体流动问题进行有效计算,还需要考虑其他许多重要方面:高效、稳定地处理时间步进;有效地实现隐式和在某种程度上呈显式的时间步进;求解大型线性方程组等等。未来,我们还有大量工作要做,仍然存在许多改进不同方法和技术的可能性!
我们 COMSOL 公司一直致力于采用有限元法提供最高效、最前沿的技术,同时致力于开发最好的通用方法——不仅适用于多物理场问题,而且适用于 CFD 等“单”物理场应用。



评论 (0)