当你在评估使用 COMSOL Multiphysics ® 软件模拟的设备、系统或进程的性能或特性时,数据集的标准差和平均值等统计量可能很有价值。这篇博客,我们将了解 COMSOL Multiphysics 中用于计算和可视化统计量的函数、绘图和其他工具。
统计学:概述
统计是指计算出表示或显示数据的值和变化的结果。下表列出了 COMSOL Multiphysics 中一些最常见的统计测量值以及它的算子和数据集操作名称:
| 测量值 | 参数 | 算子名称 | 数据集操作名称 |
|---|---|---|---|
| 平均值 | \mu | mean, timeavg |
平均值 |
| 标准差 | \sigma | stddev |
标准差 |
| 方差 | 变量,\sigma^2 | – | 方差 |
下面是对这些统计测量的概述:
- 平均值 或算术平均值 (下面等式中的 \mu)是所有数据值的总和除以数据集中数据值的数量。它是一个很有用的值,可以用来表征一些波动量的水平。平均值可能对异常值(即与数据集中的其他值有明显差异的数据值)敏感。一个相关的统计量是中位数,它是将数据集的上半部分与下半部分分开的中间值(如果数据集包含偶数个值,则为两个中间值的平均值)。COMSOL Multiphysics 中的
timeavg算子可以计算一个时间间隔内随时间变化的表达式的平均值。 - 标准差 (下面的等式中的 \sigma)用于表征数据偏离实际平均值的程度。它是方差 的平方根。与方差不同的是,标准差与数据本身的单位相同。
- 方差(下面等式中的 Var)用于衡量一组数据值与它的平均值的距离,它的单位是数据的平方。
下面的等式显示了平均值 \mu 的定义:
下面的等式定义了方差:
式中,X 是要计算的方差(和平均值)的变量,x_i 是的一组取值,\mu 是平均值。方差的定义对于固定总样本是有效的。
在 COMSOL Multiphysics 中,X 和 x_i 表示一组固定的值。
标准差 \sigma 是方差的平方根:
这些统计公式可以简单的被概括为描述定义在几何实体上的统计量,其中对几何实体的求和被积分所取代,这就是 COMSOL Multiphysics 的计算方法。变量 X 在 \Omega 域上的平均值的积分形式为
同样,变量 X 的方差在 \Omega 域上可以表示为
\int_\Omega (x-\mu(x))^2 d\Omega
式中,|\Omega| 是域的大小(体积、表面或长度,取决于模型的空间维度)。
接下来,我们将介绍如何在 COMSOL Multiphysics 仿真中使用这些操作和算子。
COMSOL Multiphysics 中的统计量
非局部耦合算子
稍后,我们将看到如何使用内置算子 stddev 计算一个表达式的标准差。在这之前,让我们先看看如何计算一个计算量的平均值,例如在一个域内或沿边界。右键单击感兴趣的 组件 节点下的 定义 节点,然后从非局部耦合 菜单中选择平均值。这样就会创建一个平均算子,默认情况下为 aveop1,在其设置中,首先定义几何实体层(例如边界),然后定义要计算的平均值的边界(或其他几何实体,取决于所选的实体层)。我们还可以用相同的方式添加算子来计算积分、最大值和最小值。
我们可以在模型中和后处理过程中使用我们创建的算子。例如,在流体流动模拟中,可以使用在出口边界定义的平均算子来计算平均流出速度。为此,我们在结果 部分的派生值 下的全局计算 节点,添加一个类似aveop1(spf.U) 的表达式,然后点击计算。在瞬态模拟中,每个输出时间的平均速度就会出现在一个表格窗口中。
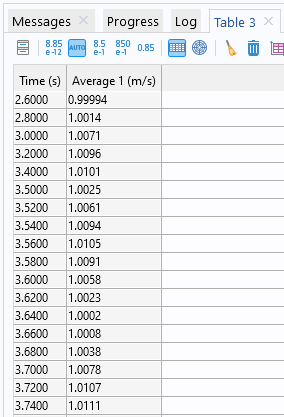
一个 表格窗口,包含每个输出时间的平均速度值。
我们可以使用非局部耦合算子计算标准差或方差两次:一次是计算平均值,一次是计算标准差或方差。例如,使用我们在流体流动示例中为出口边界定义的平均算子 aveop1,使用全局计算 节点和表达式 sqrt(aveop1((aveop1(p)-p)^2)) 计算标准偏差,该表达式实现了上述边界上压力标准偏差的方程。
使用表达式运算符简化
上述表达式 sqrt(aveop1((aveop1(p)-p)^2)) 有点长,所以如果我们想在几个地方使用它,可以定义一个表达式运算符 来简化它。首先,需要在显示更多选项 对话框的常规 部分下启用变量实用程序。然后,右键单击组件 下的定义 节点时出现的变量实用程序 子菜单添加一个表达式运算符 节点。在表达式运算符 节点的设置中,我们定义了一个算子,例如 stdop1,使用与上述类似的表达式,但其输入参数由我们选择,例如 pin,如下图所示:
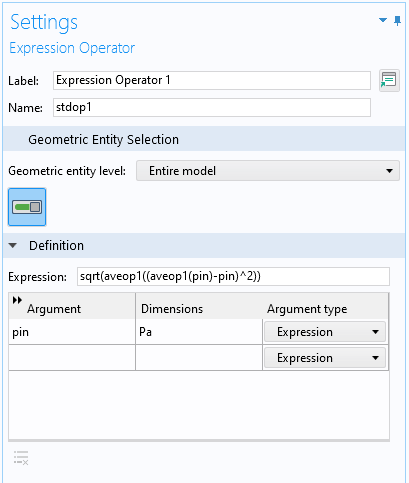
表达式运算符节点的 设置 窗口,为标准差定义一个简化的算子 stdop1。
然后,我们可以在后处理中使用这个算子,键入 stdop1(p) 而不是 sqrt(aveop1((aveop1(p)-p)^2))。
派生值
出于后处理目的,我们可以添加体积平均、表面平均值 和线平均值 节点,可以通过右键单击派升值 节点然后从平均值 子菜单中选择其中一个选项来实现。我们可以为积分、最大值 和最小值 定义类似的节点。
时间序列和参数扫描的转换
例如,在使用点计算 特征计算来自瞬态、参数化或特征值解决方案的数据时,我们可以对系列数据应用以下操作之一:
- 平均值
- 积分
- 最大值或最小值
- 均方根 (RMS)
- 标准差
- 方差
每个操作都提供一个输出,它可以是参数扫描值中的平均值或瞬态模拟中某个点的量的标准偏差。
内置算子
在计算和绘制 COMSOL Multiphysics 仿真结果时,我们可以访问大量物理场专用变量以及内置的物理和数学常数、函数和算子。我们可以将它们直接输入到任何表达式 字段中,也可以单击添加表达式 或替换表达式 按钮(可在结果功能的表达式 部分工具栏中找到)。下面屏幕截图显示了 COMSOL Multiphysics®6.0 版本中积分和统计信息 中可用的算子:

可用于积分和统计的算子。
这里有一个特别算子 stddev,我们可以用它来计算表达式的标准偏差。可以使用达式 stddev('comp1.aveop1',p) 来计算上述相同出口边界压力下的标准偏差,这是一种比上一个标准偏差表达式中使用的对平均运算符的嵌套调用更直接、更有效的语法。请注意,这里给出的组件和运算符名称只是示例,在您的模型中可以使用其他名称。
一个标准差和平均值的例子
作为示例,我们来计算圆柱绕流模型的几个瞬态统计值,该模型可在软件案例库中的流体动力学 文件夹中找到。我们将计算以下值:
- 模拟的所有时间步长的计算域中压力的平均值和标准差
- 在所有时间步长上计算的出口边界点处速度的平均值和标准差
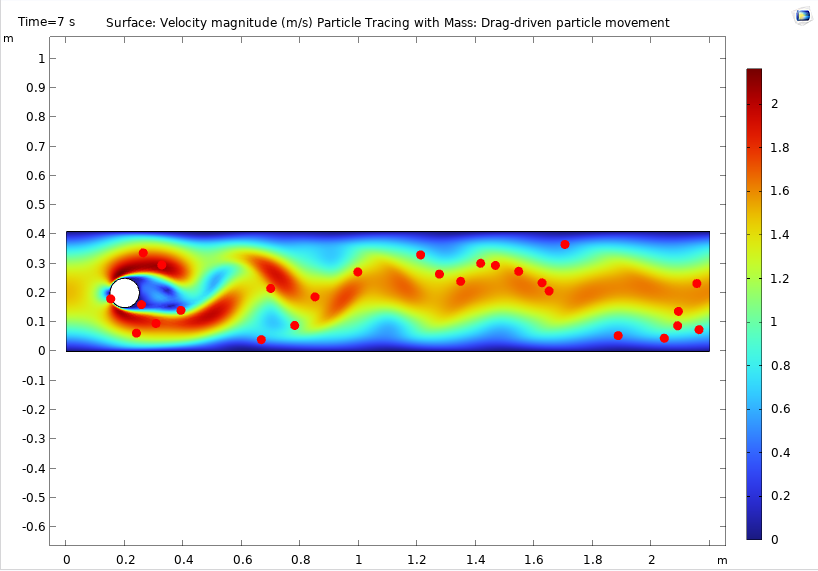
圆柱绕流模型的默认绘图,显示了模拟结束时间(7s)的速度场和粒子运动。
域内和出口边界压力的平均值和标准差
为了计算域内的压力的平均值和标准差,首先添加一个平均值 非局部耦合节点,例如 aveop2,并在域中定义它(这个几何结构中只有一个域)。计算解后,我们可以在结果 部分的派生值下添加一个全局计算 节点,使用表达式 aveop2(p) 计算平均压力。然后,所有从时间选择 列表中选择的时间的平均压力将显示在表格 窗口中。(默认是包括所有时间步长)如果要计算所有时步的平均压力,从数据序列运算 部分中的转换 列表选择平均值。对于平均压力的平均值,这时输出的是一个单个标量数。对于每个时步的标准偏差,使用表达式 stddev('comp1.aveop2',p)(或上述任何其他选项)。
stddev 算子的参数不一定要是平均值。作为替代,比如我们可以传递给它一个积分耦合算子,它仍然会计算平均值的正确标准差。我们还可以将它与 timeavg 算子结合使用,用于产生与在其他地方获得的相同结果,方法是使用类似 stddev('timeavg',t1,t2,expr) 的表达式对时间序列进行数据运算,其中 t1 和 t2 分别是开始时间和停止时间,expr 是计算该时间间隔内时间平均值的表达式。例如,为了将沿出口边界的每个点的压力的时域标准差绘制为从 6s 到 7s 的时间平均值,可以使用 stddev('timeavg',6,7,p) 表达式。
线结果图的 设置窗口,其时域标准差表达式为从 6s 到 7s 的时间平均值。
相应的绘图显示了压力的标准偏差在出口边界的中间最小。
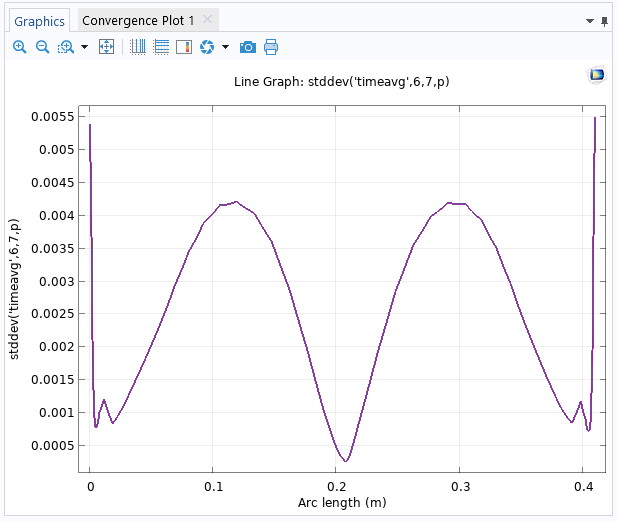
出口边界处时域标准差的 线结果图。
出口速度的平均值和标准差
如果我们想在所有时步上计算出口边界中点的平均值和标准偏差,就必须首先确定该点的速度。可以使用两种方法执行此操作:
- 在输出边界中间的几何结构中添加一个点,即使创建几何结构时不需要它
- 添加一个切割点数据集(在本例中为二维截点),然后在数据集的设置中定义截点的坐标
要计算中点处的速度,请使用点计算 节点并选择已经定义的点或使用二维截点 数据集作为输入数据集(取决于为点数据选择的方法)。例如,使用 spf.U,作为速度大小的表达式。在数据系列运算 部分,选择平均值,然后选择标准差,每次选择后单击设置 窗口顶部的计算,可以获得模拟中的所有时间步出口中点处速度大小的平均值和标准偏差(单位均为 m/s)。

表格窗口,显示了相同数量的平均速度大小和标准偏差。
直方图
直方图可用于说明某些数据的形状和分布。COMSOL Multiphysics 中的绘图工具包括以下类型的直方图:
- 直方图 (一维和二维图),显示数量如何在几何体(即网格体积)上分布。在一维直方图中, x 轴表示数量的值(作为区间的数量或值的范围),y 轴表示每个区间中总单元体积的计数。
- 表直方图(一维和二维图),类似于直方图,基于来自表或计算组的数据。
- 矩阵直方图(仅限二维图),当有一个预计算的矩阵并希望将它可视化为二维直方图时,可以使用它。
对于直方图 和表格直方图,我们可以选择是要指定直方图中的 bin 数量,还是要指定直方图 bin 的限制范围。对于任何一个二维直方图,我们添加一个高度表达式 子节点来绘制沿 z 轴的 bin 大小,如下面的三维直方图所示。
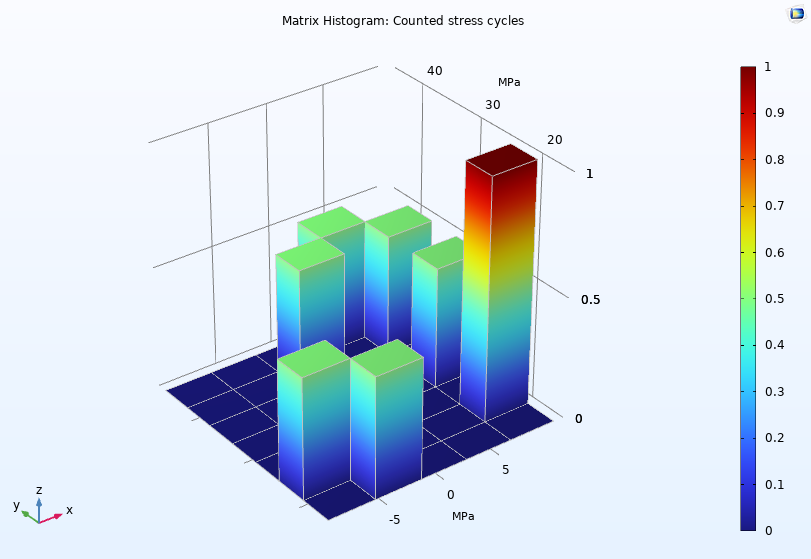
疲劳分析中的循环计数-基准模型,矩阵直方图显示计算的应力循环。
不确定性量化和统计
使用 COMSOL Multiphysics 的附加产品不确定性量化模块,可以直接在输出表组中访问与不确定性量化仿真相关的统计数据。例如,对于使用非自适应高斯过程代理模式的不确定性传播(UP)分析,可以使用下列 4 个表:
- QoI 置信区间 表,其中每个关注量 (QoI) 包含一行,列表示平均值、标准差、最小值和最大值,后面是 90%、95% 和 99% 可能性的置信区间。
- UP 预测 QoI 表,其中包含蒙特卡罗采样点的 QoI 的代理模型预测值。
- UP 预测标准差 表,其中包含蒙特卡罗采样点的代理模型预测标准差。这可以看作是内置的代理模型误差估计。
- 最大熵 表,其中包含最大相对标准差,每个 QoI 一个。
当使用自适应高斯过程代理模型时,4 个对应的自适应结果表也被添加到输出表组中。它们包含所有适应步骤的结果信息。
下一步
接下来,你可以在自己的仿真模型中尝试其中一些统计工具;你可以获得感兴趣的变量或参数的变化和特征的统计值并对它们进行量化。如果你对这个主题有任何疑问,请点击下面的按钮联系 COMSOL。



评论 (0)