理解和表征模型的不确定性
“不确定性量化模块”旨在帮助用户分析关注量与模型输入之间的相关性，以理解模型不确定性对分析结果的影响，为参数筛选、灵敏度分析、不确定性传播和可靠性分析等提供了一个通用界面。
“不确定性量化模块”可以有效地验证模型假设的有效性、可靠地简化模型、了解影响结果的关键模型输入、探索关注量的概率分布，并确认设计的可靠性。通过确保模型的准确性并深入理解分析结果，将有助于降低生产、开发和制造成本。
“不确定性量化模块”可以与 COMSOL 产品库中的各种产品相结合，用于分析电磁、结构、声学、流体流动、传热和化学工程仿真的不确定性。此外，将其与“CAD 导入模块”、“设计模块”或任意 CAD LiveLink™ 产品结合使用，可以进一步扩展应用范围，实现更全面的功能。
联系 COMSOL
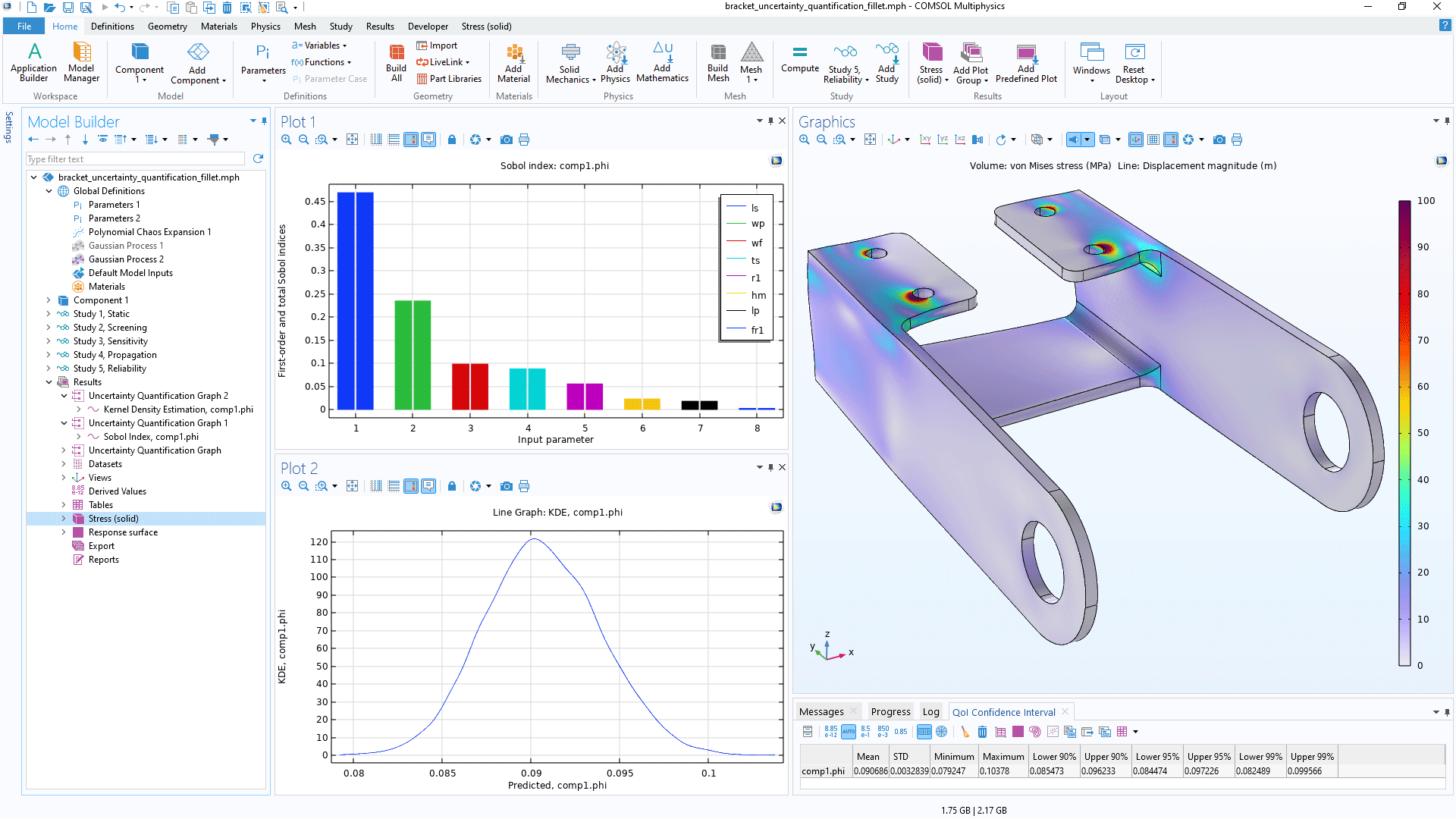
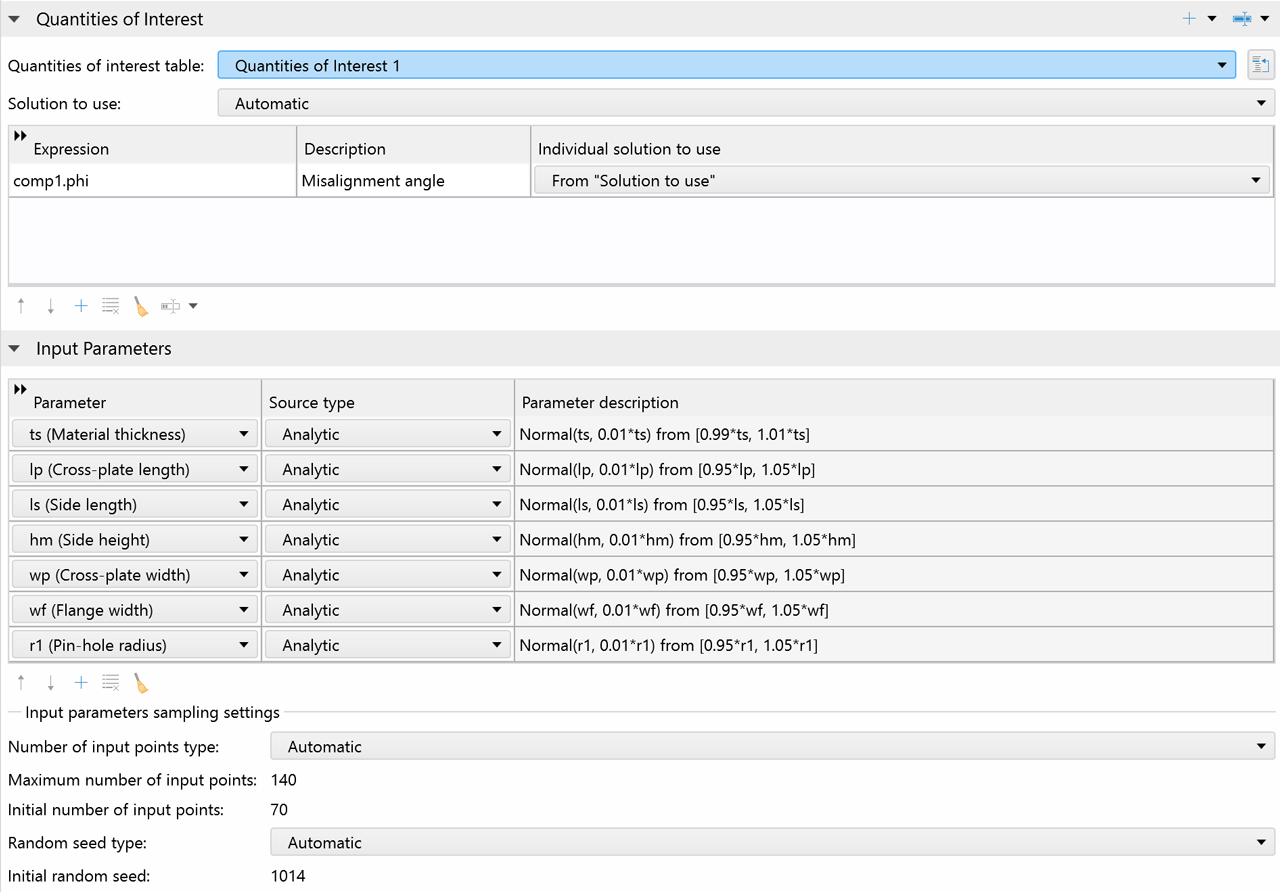
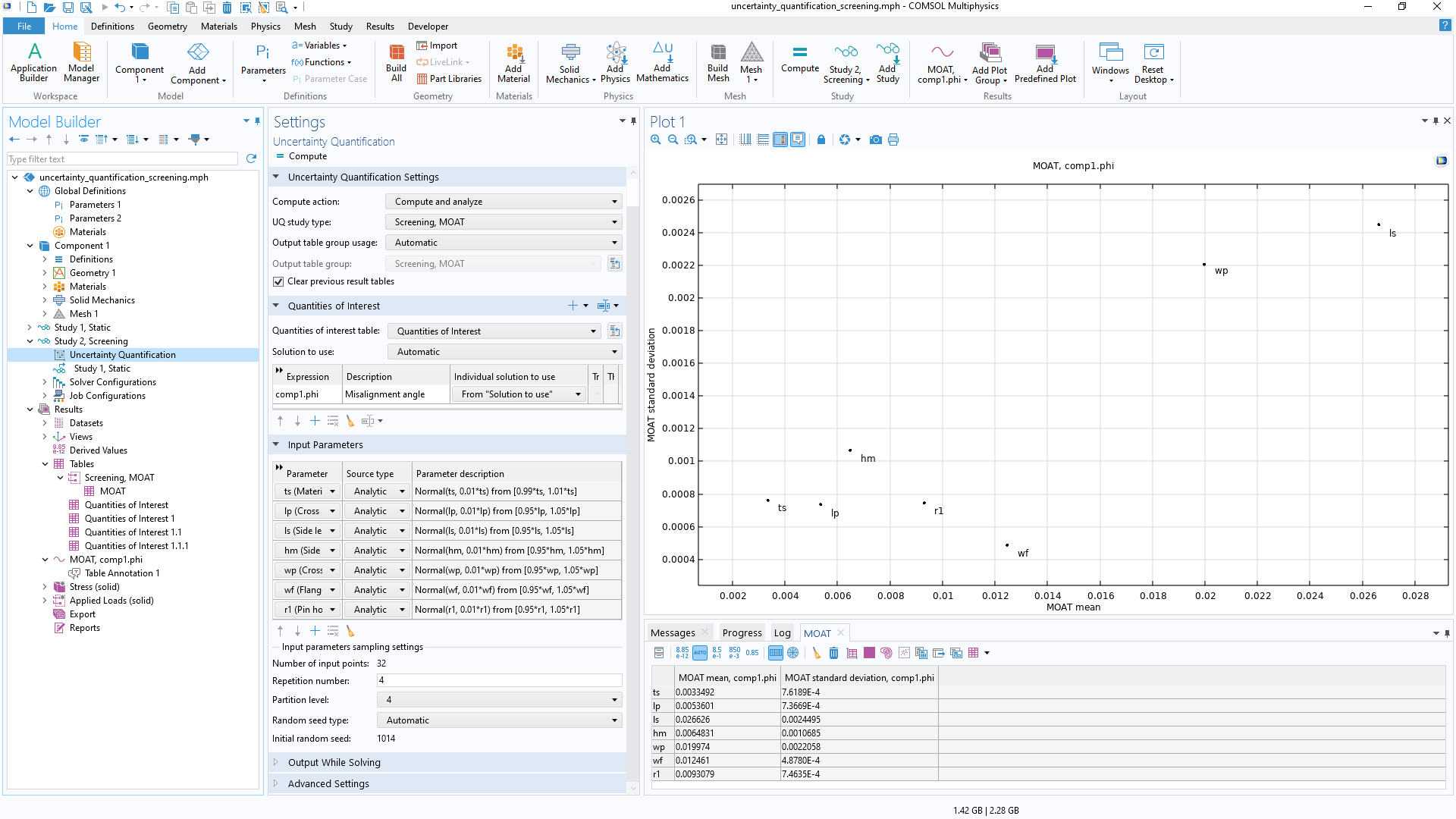
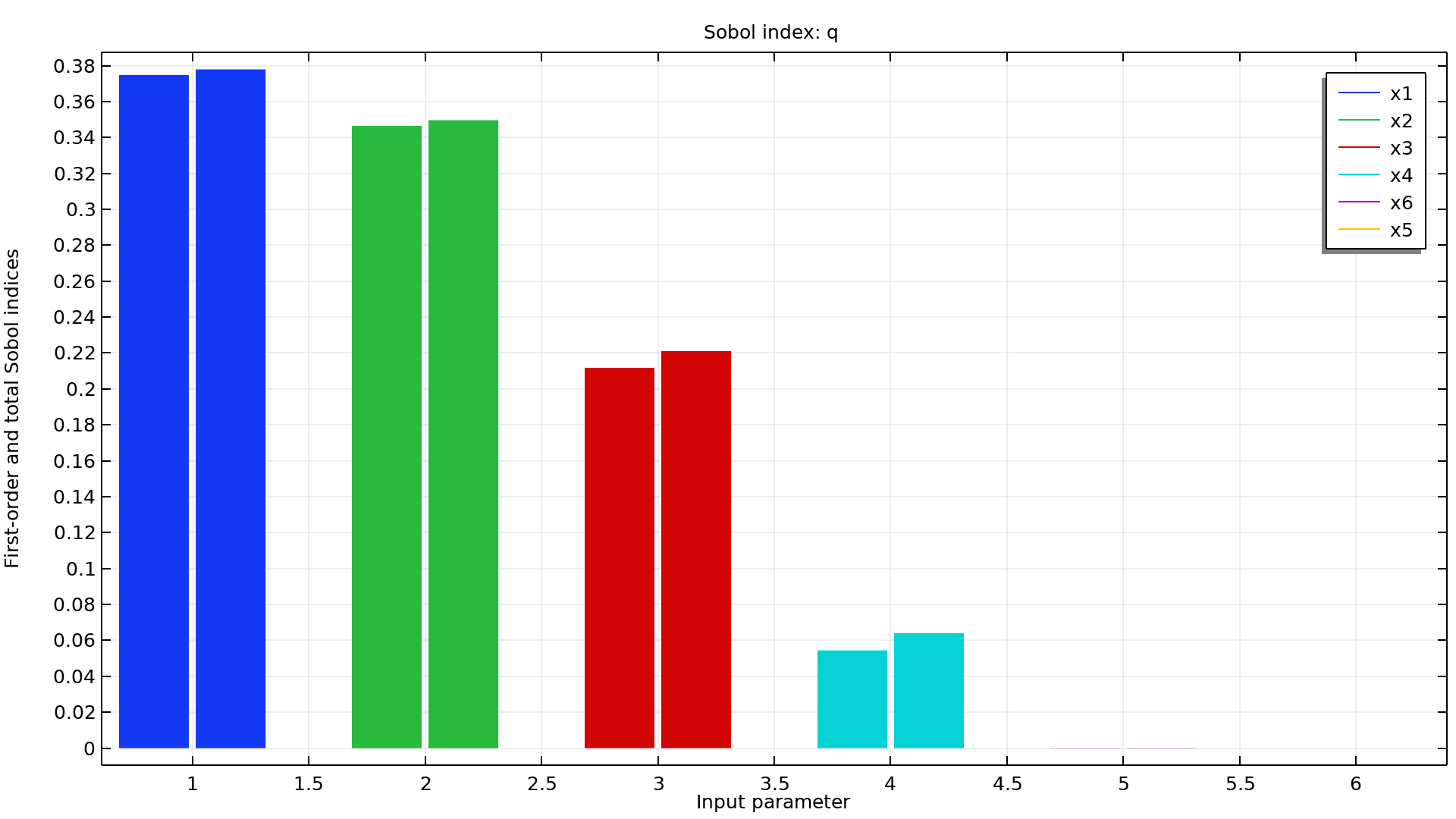
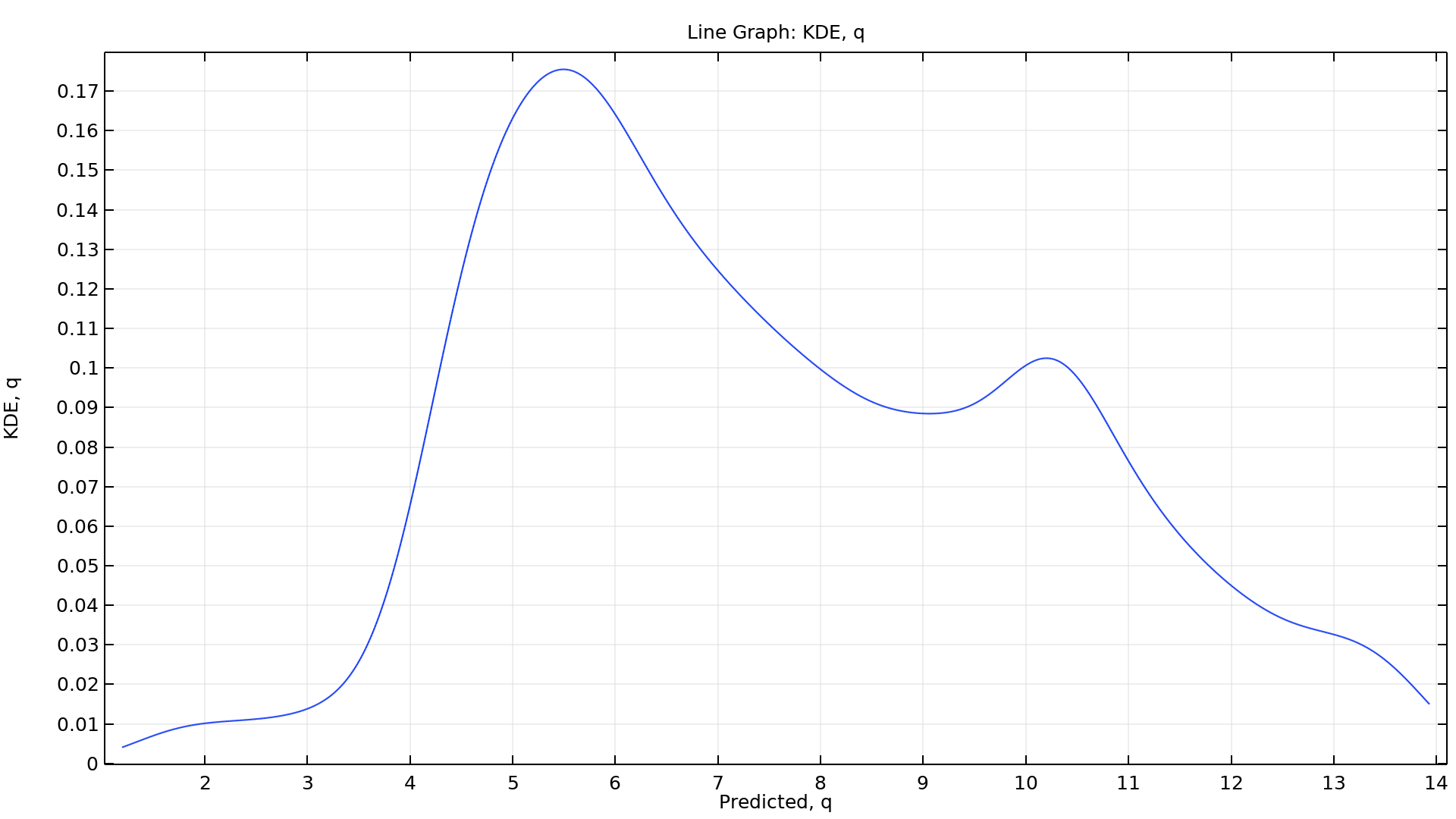
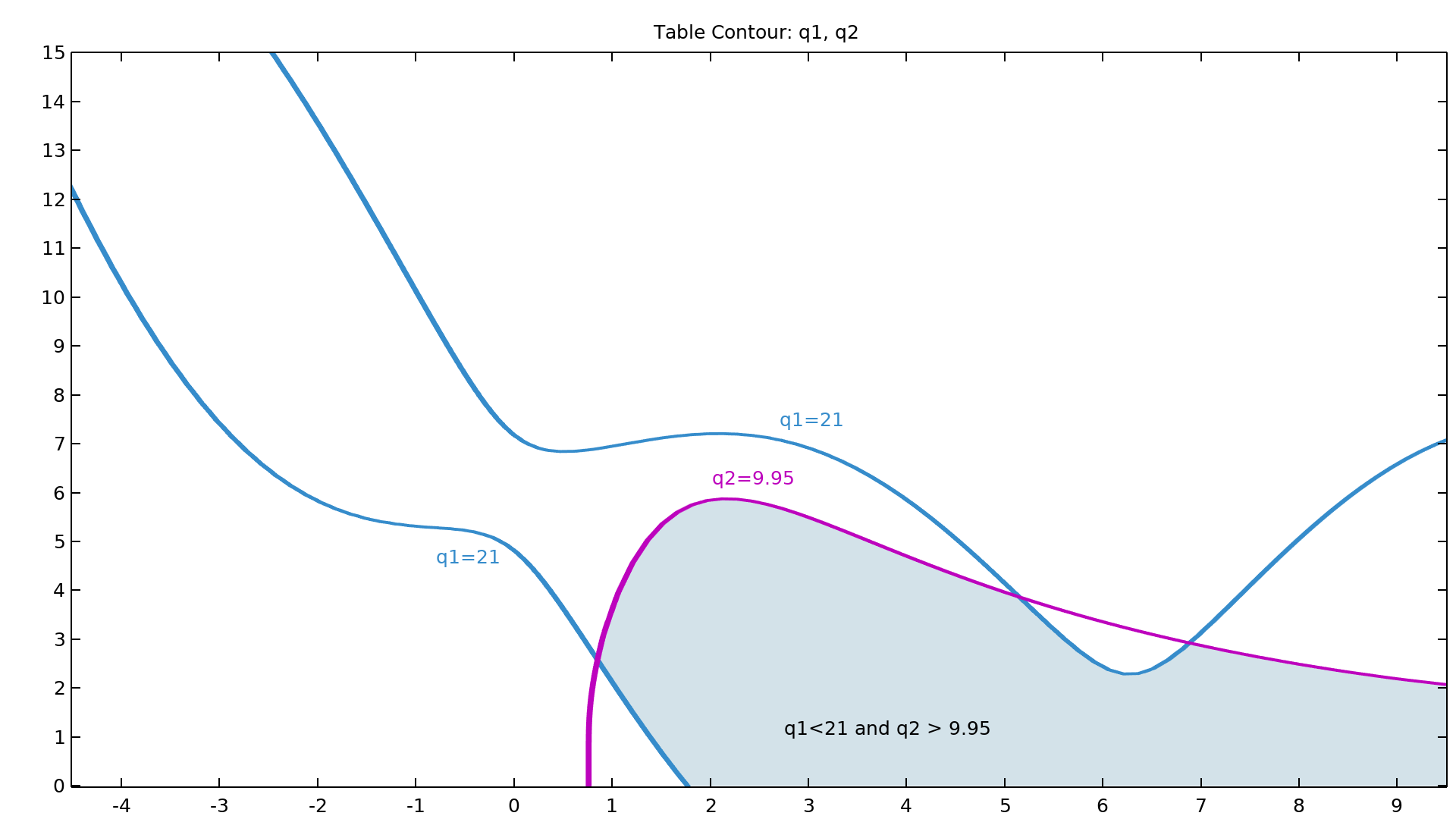
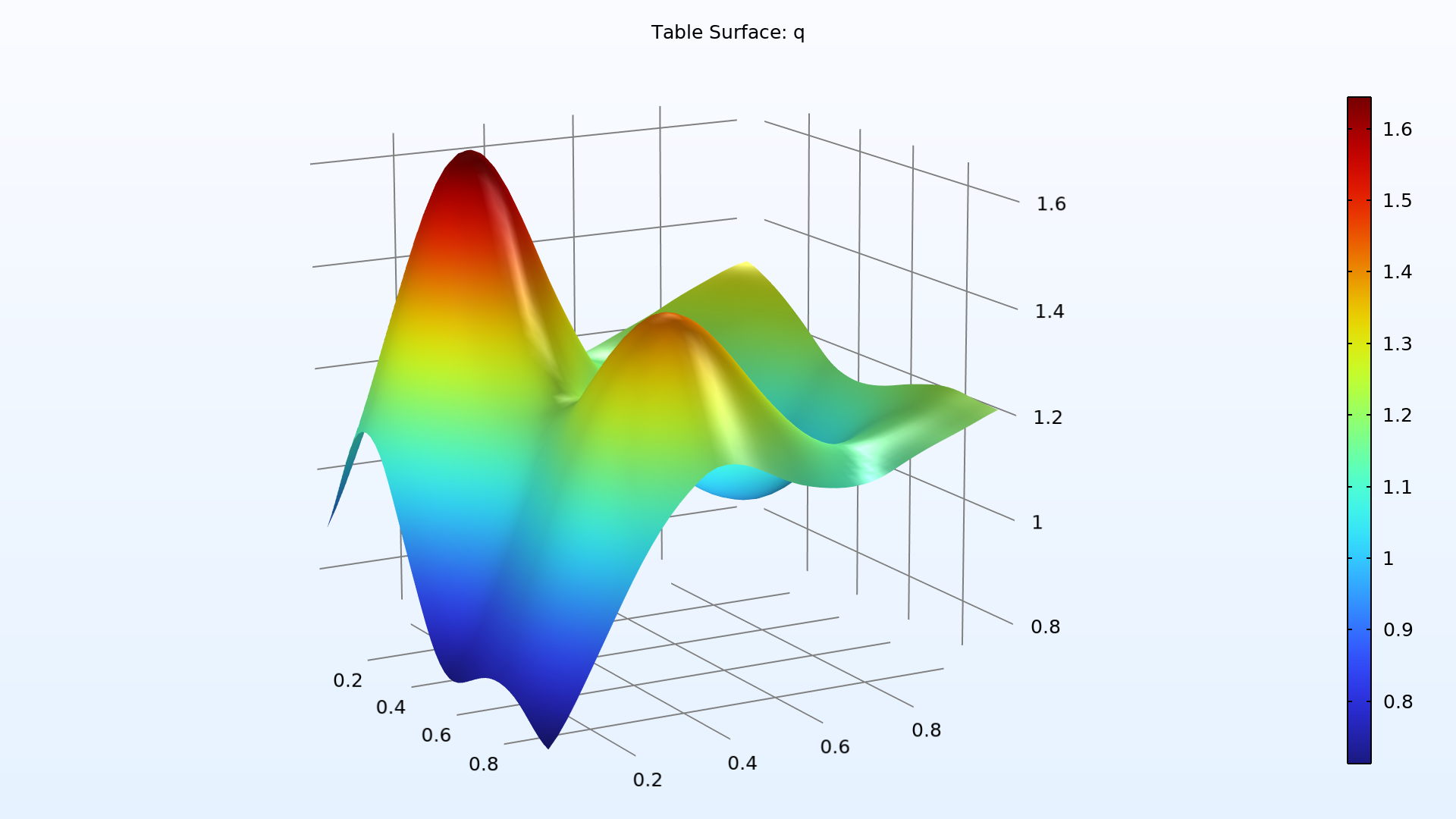
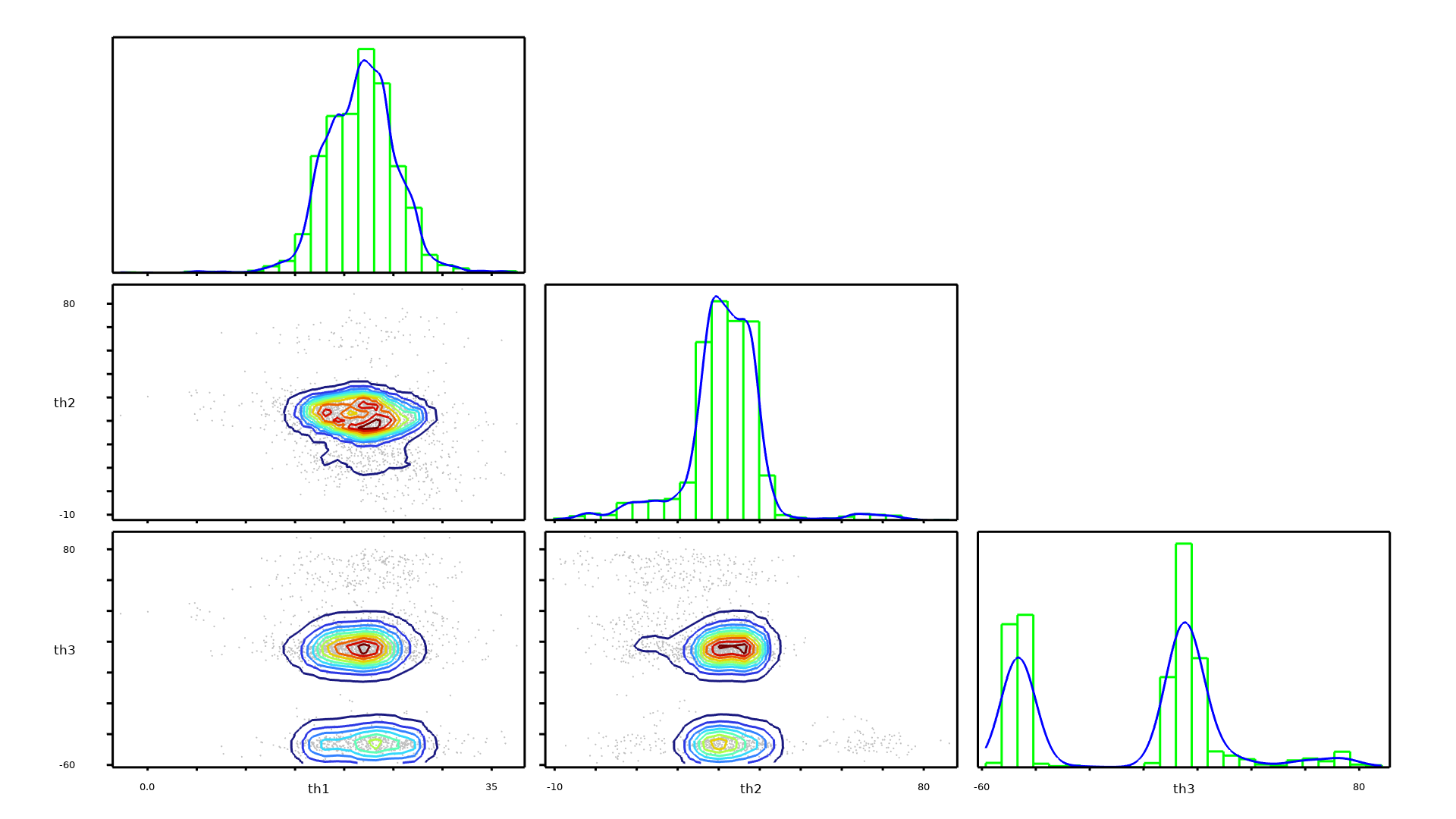
在运行不确定性量化研究时，用户可以基于 COMSOL Multiphysics® 模型的结果来定义关注量，使其成为输入参数的函数。
对于结构分析，关注量可以是最大位移、应力或偏转角。在传热或 CFD 分析中，关注量可以是最高温度、总热损耗或总流体流率。对于电磁仿真，关注量可以是电阻、电容或电感。由于“不确定性量化模块”适用于使用 COMSOL Multiphysics® 软件计算的任何物理场模型以及各种求解场量的数学表达式，因此关注量的选择是无穷无尽的。
无论是物理场设置、几何尺寸、材料属性还是离散化设置，任何不确定的模型输入都可以作为输入参数，并且任何模型输出都可以用来定义关注量。
筛选，MOAT 研究基于一种轻量级的全局筛选算法，可以对每个输入参数的重要性进行定性度量。该方法完全基于样本数据，利用了 Morris one-at-a-time（MOAT）方法，与传统方法相比，它所需的 COMSOL 模型计算量较小。当输入参数的数量太大而无法进行计算成本较高的不确定性量化研究时，这种方法将成为您理想的选择。
使用 MOAT 方法，可以为每个关注量计算每个输入参数的 MOAT 平均值和标准差，并将它们显示在 MOAT 散点图中。通过对 MOAT 平均值和标准差进行排序，可以揭示输入参数的相对重要性。较高的平均值表示该参数对关注量有显著影响，而较高的标准差则表示该参数的影响是复杂的：可能与其他参数有很强的相互作用，或者具有非线性影响，甚至可能同时具备这两个因素。
灵敏度分析 是一种研究类型，用于计算关注量对输入参数的敏感性，包含两种方法：Sobol 法和相关法。
Sobol 法可用于分析整个输入参数分布，并将每个关注量的方差分解为输入参数及其相互作用的贡献之和。
利用 Sobol 法，可以计算每个输入参数的 Sobol 指数。一阶 Sobol 指数显示由各个输入参数的方差产生的关注量的方差，而总 Sobol 指数则显示由每个输入参数的方差及其与其他输入参数的相互作用而产生的关注量的方差。如果将每个关注量和所有参数的 Sobol 指数以直方图的形式显示在专用的 Sobol 图中，并按照总 Sobol 指数进行排序，关注量对总 Sobol 指数最高的输入参数最为敏感。通过比较输入参数的总 Sobol 指数和一阶 Sobol 指数之间的差异，可以衡量该输入与其他输入之间相互作用的影响程度。
与筛选方法相比，灵敏度分析能够定量分析关注量的不确定性如何分配给不同的输入参数。然而，这种方法需要更多的计算资源，因为准确计算 Sobol 指数需要高质量的代理模型支持。
另一种方法是相关法，可用于计算每个输入参数与关注量之间的线性和单调关系。通过基于相关法的灵敏度分析，可以计算四种类型的相关性：双变量相关、等级双变量相关、偏相关或等级偏相关。
不确定性传播 研究类型用于通过计算概率密度函数（PDF）来分析输入参数的不确定性如何影响每个关注量。然而，大多数通过 COMSOL Multiphysics® 模型计算将输入参数与关注量进行映射的底层物理应用通常无法进行解析计算。
因此，为了得到 PDF 的近似值，需要进行蒙特卡罗分析。与 Sobol 法类似，使用代理模型可以显著降低蒙特卡罗分析的计算成本。对于每个关注量，都可以执行核密度估计（KDE），并为其生成可视化效果图，作为 PDF 的近似值。此外，置信区间表可以基于此分析给出每个关注量的平均值、标准差、最小值、最大值，以及对应于 90%、95% 和 99% 置信水平的下限值和上限值。
与用于探索关注量的总体不确定性的其他不确定性量化研究类型相比，可靠性分析，EGRA 方法提供了一种更直接解决问题的方式。在给定标称设计和一些特定的不确定输入的情况下，设计失败的概率是多少？这里的失败可以是指设计的完全失效，也可以通过质量准则来表述。
为了确保可靠性，传统的建模仿真方法通常使用安全裕度和最坏情况进行评估。然而，通过适当的可靠性分析，可以计算实际概率，避免对结果进行高估或低估。从每个关注量的不确定性传播的置信区间表中可以得到粗略估计，但是通过可靠性分析，您可以根据关注量和相应阈值的组合来定义更复杂的可靠性准则。用于可靠性分析研究的高效全局可靠性分析（EGRA）方法可以有效地将计算资源引导至能够区分设计失败和成功的极限状态。
使用 Sobol 法计算的灵敏度分析、不确定性传播和可靠性分析都依赖于精确的蒙特卡罗型分析，这通常需要大量的计算才能获得良好的准确性。对于 COMSOL Multiphysics® 模型计算可能需要大量资源且不确定性量化分析涉及多个参数的现实问题，仅仅使用 COMSOL Multiphysics® 模型计算进行的蒙特卡罗分析在计算上并不可行。为了解决这个问题，“不确定性量化模块”引入了一个关键功能，其特点是：能够针对特定的 UQ 分析训练和使用代理模型（也称为元模型），以节省计算资源。
代理模型是一种紧凑的数学模型，用于表示和计算关注域中由输入参数定义的关注量。这种模型完全独立于基础 COMSOL Multiphysics® 模型，并且在经过适当的训练后，可用于代替 COMSOL Multiphysics® 模型来预测其他输入参数值的关注量的值，而不是求解的值。代理模型的构造过程通常是自适应的，并且可以高精度地逼近原始模型。用户定义的容差可以提高代理模型的准确性，但更高级别的准确性需要额外的 COMSOL Multiphysics® 模型计算支持。
一旦建立代理模型，您就可以进行独立验证以进一步测试其有效性，并可以快速计算整个输入参数空间的响应面数据。然后，可以通过可视化来展示响应面，其中每次绘制一个关注量与两个输入参数之间的关系。
当某些输入参数具有未知的概率分布（称为校准参数）时，需要使用“逆不确定性量化”（逆 UQ）。逆 UQ 通过向后传播实验数据，可以帮助我们更加深入地了解这些校准参数的统计属性。为了应用逆 UQ，需要在分析之前为每个校准参数设置一个先验概率分布。
实验数据通常可用于关注量和实验中使用的参数。此外，还存在一些无法直接测量的校准输入参数。举个例子，假设我们进行一个实验，旨在校准一个机械零件的杨氏模量。我们应该进行实验来测量作为指定材料位移的函数的拉应力，然后通过设置逆 UQ 研究，结合实验数据和杨氏模量的先验知识，可以校准概率分布，从而以最佳方式重现实验中拉应力的测量值。逆 UQ 可应用于各种基于物理场的模型，包括与结构力学、流体流动、声学、传热、电磁和化学工程有关的模型。
为了实现校准参数的后验概率分布计算，可以将代理模型与马尔可夫链蒙特卡罗（MCMC）方法结合使用。计算完成后，可以将校准输入参数的联合概率分布和边际概率分布可视化。此外，软件还会生成一个置信区间表，提供各种信息，包括平均值、标准差、最小值和最大值，以及对应于每个校准输入参数的 90%、95% 和 99% 置信水平的下限值和上限值等。
COMSOL 是否能用于解决我的问题？
欢迎联系我们，我们的专业工程师可以协助您评估技术可行性，并根据使用场景推荐许可形式。
点击右侧的“联系 COMSOL”按钮，填写并提交信息，我们的工作人员将会尽快与您联系。
评估与试用 COMSOL® 软件