微流体模块
多物理场仿真助力微流体装置研究
“微流体模块”是 COMSOL Multiphysics® 的一款附加产品,为研究微流体装置提供了易于操作的功能,其重要应用包括芯片实验室设备、数字微流体、电动和磁动装置以及喷墨打印机的仿真。“微流体模块”可用于模拟蠕动流、层流、多孔介质流、多相流和滑移流,并能够在二维和三维中求解稳态和瞬态流动问题。此外,当与 COMSOL 产品库中的其他模块耦合使用时,还能够扩展到更多领域的多物理场耦合仿真,包括流-固耦合、热流等多物理场现象。
联系 COMSOL
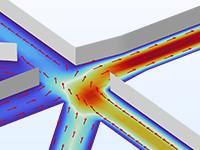
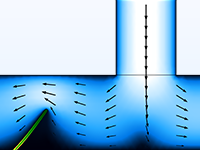
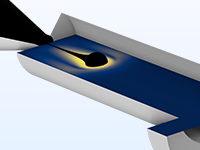
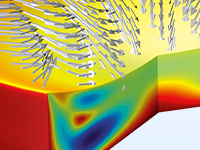
微流体模块支持的建模对象
借助 COMSOL® 软件,您可以进行各种微流体分析。
微流体模块的特征和功能
“微流体模块”提供了一系列强大的功能,可以解决各种仿真问题。
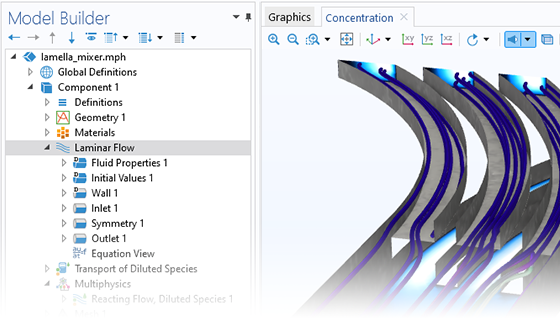
单相流
流体流动 接口使用物理量(如压力和流率)以及物理属性(如黏度和密度)来定义流体流动问题。层流 接口广泛涵盖了不可压缩流和弱可压缩流的仿真,并支持模拟非牛顿流体流动。对于雷诺数明显小于 1 的情况,还可以使用蠕动流接口,通常也称为斯托克斯流,主要适用于微流体装置中黏性流动占主导的情况。
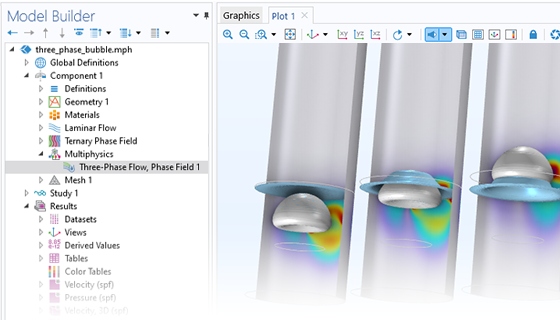
三相流
层流三相流,相场 多物理场接口用于跟踪三种不混溶且不可压缩流体之间的界面。我们假设流动为层流,适用于低至中等雷诺数,并且各相的密度保持恒定。通过求解动量守恒的纳维-斯托克斯方程和质量守恒的连续性方程,以及四个附加的输运方程(两个用于相场变量,两个用于广义化学势)来跟踪界面的位置,其中的表面运动由最小化自由能来确定。此外,三元相场 接口还能够通过求解两个相场变量和两个广义化学势变量来跟踪三种不混溶流体之间的移动界面。
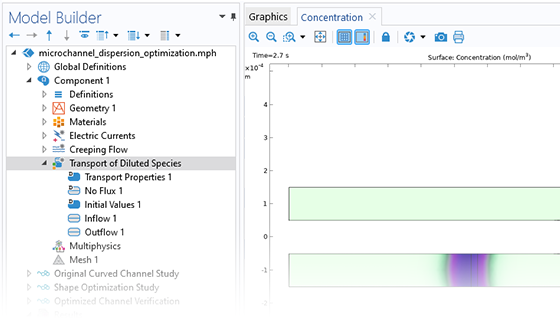
物质传递
“微流体模块”提供了一个专用的接口用于分析稀物质传递,可用于模拟化学物质在电场中通过扩散、对流(与流体流动耦合时)和迁移进行的传递过程,其中一种成分(溶剂)过量(大于等于 90 mol%)。本模块通常用于对混合器的性能进行建模,为了模拟微流体装置中的化学反应,还可以将“微流体模块”与化学反应工程模块结合使用,通过二元扩散实现浓物质传递。
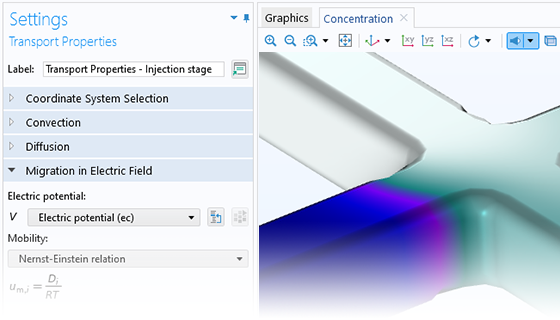
电动流动
在进行稀物质传递建模时,可以根据能斯特-普朗克方程来描述离子在静电场中的电迁移。这一功能的应用包括电泳迁移率和电渗流,即电动流动。通过将“微流体模块”与“化学反应工程模块”耦合使用,您可以方便地使用专为电解质建模而设计的 能斯特-普朗克 和 电泳输送 接口,并可以包含泊松方程的公式或电荷平衡的电中性条件。通过综合运用能斯特-普朗克方程与泊松方程,可以模拟双电层和电渗流现象。
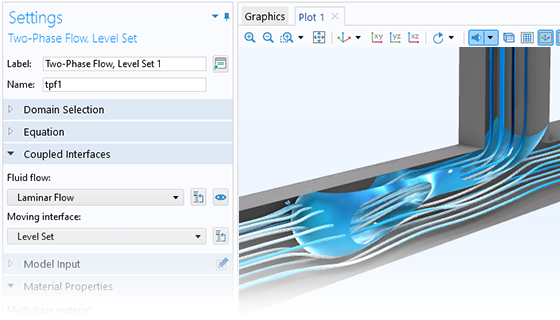
两相流
“微流体模块”提供了三种不同的方法来模拟两相流:水平集方法、相场法和动网格方法。这些方法适用于模拟由运动流体界面分隔的两种流体,并能够详细跟踪界面的属性,包括表面曲率和表面张力。水平集和相场方法采用固定背景网格,并求解额外的方程来跟踪界面的位置。而动网格方法求解动网格上的流动方程,并在表面直接施加表示流体界面的边界条件。在这种情况下,可以采用任意拉格朗日-欧拉(ALE)方法来求解网格变形的附加方程。所有这些方法及其接口都支持可压缩和不可压缩层流,其中一种或两种流体可以是非牛顿流体。
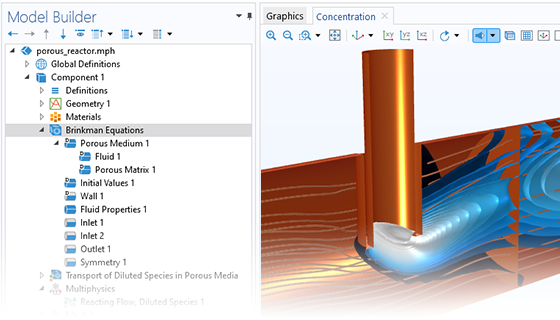
多孔介质流动
在微观几何结构中,多孔介质流动是一种常见现象。当孔径在微米范围内时,流动通常以摩擦为主;在这种情况下,可以使用达西定律来求解流动问题。为了满足这一需求,“微流体模块”提供了基于达西定律的多孔介质流动专用接口,其中忽略了与流动方向垂直的剪切应力。对于中间流,我们还提供了基于布林克曼方程的接口,用于模拟穿过多孔介质的流动,其中剪切应力无法被忽略,并支持斯托克斯–布林克曼公式(适用于非常低流速的情况)和 Forchheimer 阻力(用于解释较高流速的影响)。只要马赫数小于 0.3,流体既可以是不可压缩流,也可以是可压缩流。该公式允许自由和多孔介质模型,包括使用布林克曼方程或层流的多孔介质。
这些接口适用于研究和模拟微流体多孔介质流动,典型应用包括纸芯片微流控和生物组织中的传输现象。
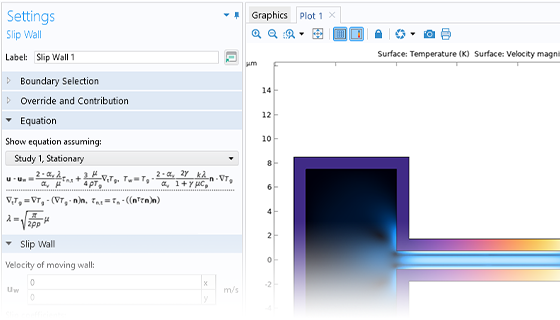
稀薄气体流动和滑移流
当分子的平均自由程与流动的长度尺度相当时,就会发生稀薄气体流动现象,这种稀薄效应对于流体的重要性可以通过克努森数 Kn 来衡量。随着气体变得更加稀薄(即克努森数增大),存在于壁面上的一个平均自由程内的克努森层开始对流动产生显著影响。当克努森数小于 0.01 时,可以忽略稀薄效应,并且“微流体模块”的层流接口可以与非滑移边界条件结合使用。对于稍微稀薄的气体(0.01 < Kn < 0.1),可以通过适当的壁面边界条件和域中的连续纳维-斯托克斯方程对克努森层进行建模。在这种情况下,可以使用“微流体模块”中的滑移流 接口。为了模拟更高的克努森数,需要使用分子流模块。
COMSOL 是否能用于解决我的问题?
欢迎联系我们,我们的专业工程师可以协助您评估技术可行性,并根据使用场景推荐许可形式。
点击右侧的“联系 COMSOL”按钮,填写并提交信息,我们的工作人员将会尽快与您联系。
下一步:
评估与试用 COMSOL® 软件