
当热辐射穿过介质时,如果介质对辐射产生吸收、发射或散射等作用,则认为该介质参与了辐射过程。本篇博客文章,我们介绍了使用多个方向的离散集方法计算热辐射的散射模型,并深入讨论了离散化方法。
参与介质中的散射
当空气粒子与太阳辐照相互作用时,大气层就是参与介质。能量的吸收和释放是由于分子或原子尺度上的能量转移引起的,而散射则是因参与介质分子对入射能量的衍射、反射和折射(参考文献1)作用导致入射能量在空间中重新分布。下图示例显示了参与介质与入射辐射的相互作用。
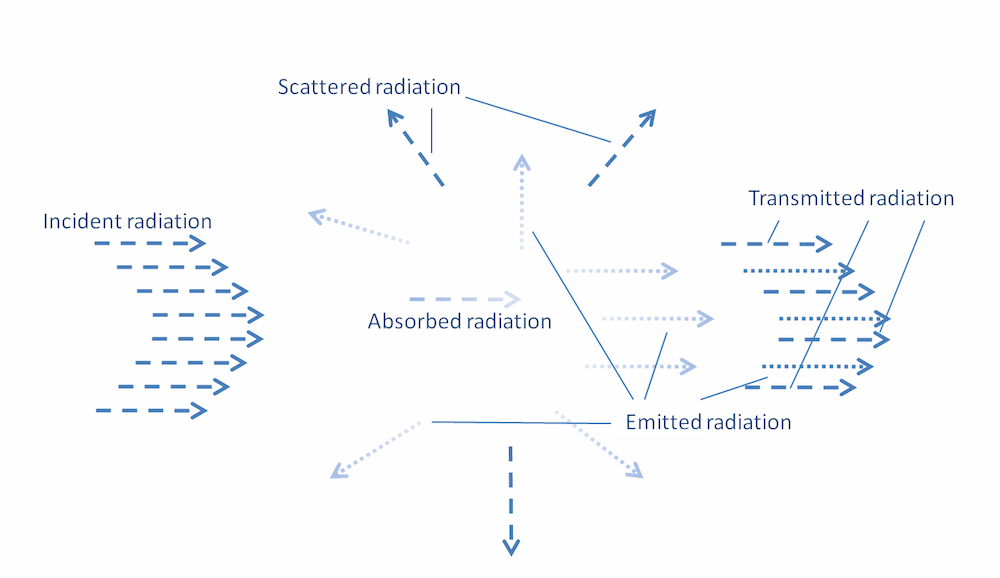
参与介质与辐射相互作用的示例。
在 COMSOL Multiphysics® 软件的附加产品——传热模块中,我们可以通过离散坐标法 将辐射传递方程离散化。该方法基于辐射的离散方向数量以及用于数值积分的相关正交权重建立。一系列离散方向和关联的正交权重的组合称为正交集。下面,我们将解释和比较 COMSOL 软件中不同物理场接口的正交集,这些接口用于吸收介质中的辐射以及与参与介质中的辐射传热。
首先,以参与介质为例。辐射强度 I 在 {\bf s} 方向(这里也可称为单位矢量)传输的守恒方程,称为辐射传递方程(RTE),表示如下
(1)
{\bf s} \cdot \nabla I({\bf r},{\bf s}) & = \kappa I_{\rm b}(T) – (\kappa + \sigma_{\rm s})I({\bf r},{\bf s}) + \mathcal{S}({\bf r},{\bf s}),\\
\mathcal{S}({\bf r},{\bf s}) & = \frac{\sigma_s}{4\pi} \int \limits_0^{4\pi}\phi({\bf s},{\bf s}’)I({\bf r},{\bf s}’)d\Omega’,
\end{split}
式中,\kappa 是吸收系数,\sigma_{\rm s} 是散射系数,I_{\rm b} 是黑体辐射强度。
d \Omega=\sin\psi d \psi d \varphi 为无穷小立体角,以球面度(sr)为单位,其中 \psi 和 \varphi 是球坐标系中 {\bf s} 方向(单位向量)的极角和方位角 (r,\psi,\varphi),如下图所示。在等式 1中,\kappa I ({\bf r},{\bf s}) 数量的能量被吸收,\kappa I_{\rm b} (T) 被发射;\mathcal{S} ({\bf r},{\bf s}) 是从任一方向散射到 {\bf s} 方向的能量总量;\sigma_{\rm s} I ({\bf r},{\bf s}) 是从 {\bf s} 方向散射至任一方向的能量总量。
对积分项 \mathcal{S} 进行离散化是一项具有挑战性的任务。需要 n 对成组的离散方向 {\bf s}_i 以及正交权重 {\bf \omega}_i,即正交集 \big((\omega_i,{\bf s}_i)\big)_{1 \leq i \leq n}。该正交集允许单位球面的数值离散化:
为了求解在参与介质中任一点沿离散方向 ({\bf s}_i)_{1\leq i \leq n} 传输的入射能量或入射辐射 G,求解等式(1)可以得到在离散方向 {\bf s}_i 传输的每个辐射强度 I_i, 1\leq i \leq n。入射辐射 G({\bf r})=\int I({\bf r},{\bf s}) d\Omega,辐射热通量 {\bf q}_{\rm r}({\bf r})=\int I({\bf r},{\bf s}) {\bf s} d\Omega 以及散射项 \mathcal{S} 的数值近似可由下式表示:
(2)
G({\bf r}) & \approx \sum_{i=1}^{n} I_i({\bf r}) \omega_i, \\
{\bf q}_{\rm r}({\bf r}) & \approx \sum_{i=1}^{n} I_i({\bf r}) {\bf s}_i \omega_i, \\
\mathcal{S}({\bf r},{\bf s}_i) & \approx \frac{\sigma_s}{4\pi} \sum \limits_{j=0}^n \phi({\bf s}_i,{\bf s}_j) I_j({\bf r}) \omega_j.
\end{split}
等式1在所有方向上的积分得到入射辐射守恒
(3)
\nabla \cdot {\bf q}_{\rm r} & = – Q_{\rm r}, \\
Q_{\rm r} & = \kappa(G-4\pi I_{\rm b}).
\end{split}
由于能量守恒,将辐射热通量 {\bf q}_{\rm r} 添加到热通量 {\bf q} = – k \nabla T 中,则计算辐射的静态能量方程变为
或
(4)
由于等式2 可以精确计算,因此入射辐射(等式3)守恒,参与介质中的辐射传热(等式4)能量守恒,这些都取决于正交集 \big((\omega_i,{\bf s}_i)\big)_{1 \leq i \leq n} 的设计。下节,我们将讨论正交集的设计。
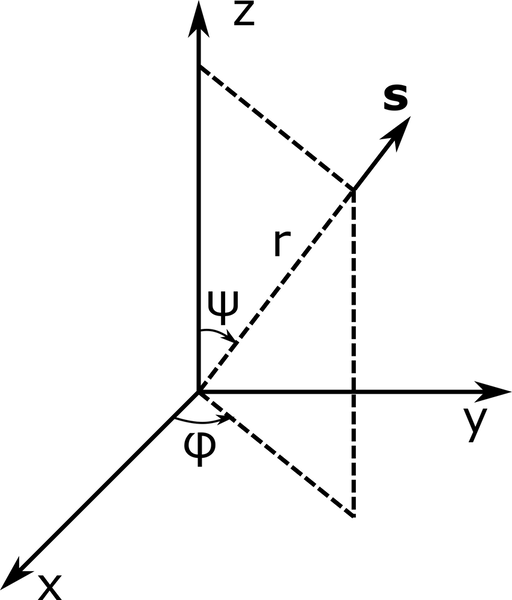
吸收、发射和散射介质的球面坐标。
设计正交集
以一种可以吸收、发射和散射能量的介质为例。为了精确计算散射项,需要满足几个矩(参考文献1)。例如,第零矩、第一矩和第二矩是
\int \limits_0^{4\pi} d\Omega & = 4\pi \approx \sum\limits_{i=1}^n \omega_i, \\
\int \limits_0^{4\pi} {\bf s} d\Omega & = 0 \approx \sum\limits_{i=1}^n \omega_i {\bf s}_i, \\
\int \limits_0^{4\pi} {\bf s}{\bf s}^\intercal d\Omega & = \frac{4\pi}{3}I_3 \approx \sum\limits_{i=1}^n \omega_i {\bf s}_i{\bf s}_i^\intercal.
\end{split}
参与介质中的辐射传热 和 吸收散射性辐射传热 接口中物理场的所有正交集,均精确满足以上这些条件。上述条件精确地近似 \int {\bf s}^k I({\bf r},{\bf s}) d\Omega, k\in \{0,1,2\},因此,期望得到各向异性散射介质(即,相函数的形式 \phi({\bf s}_i,{\bf s }_j)= \sum \limits_{k=0}^2\alpha_k ({\bf s}_i\cdot{\bf s}_j)^k). 中的吸收、发射和二阶多项式辐射传热的精确结果。对于 p^{\rm th} 阶各向异性散射,难点在于设计一个可以得到一个精确近似 \int {\bf s}^k I({\bf r},{\bf s}) d\Omega, k\in \{0,\ldots,p\} 的正交集。
在参与介质中的辐射传热和吸收散射性辐射介质 接口可应用的一些正交集,分别为:
- 偶数级对称(LSE)
- 混合极对称(LSH)
- 等权重奇数(EWO)
- 准均匀
其中,LSE,LSH 和 EWO 是条件正交集,它们的高阶矩条件不同(有关更多信息,请参考参考文献2)。N 阶离散化由 SN 表示,并在三维中有 N(N+2) 个离散方向。对于相同的离散化阶数(例如 S6),根据参考文献2,正交集 LSH 和 EWO 可以对热通量进行更好地计算。下一节,我们将进一步讨论这一论点。但是,众所周知,当第一力矩满足半球形条件时,壁面辐射热通量的计算更为精确(参考文献1),这意味着
(5)
因此,需要讨论和比较任意几何的正交集表现,等式5不是所有边界的先验条件。
准均匀正交集是按几何级数生成的。N 阶离散表示为 TN 并且在 3D 中有 8N^2 个离散方向,这意味着在第一个八分圆 \{(x,y,z),x \geq 0,y \geq 0, z \geq 0 \} 有 N^2 个方向 。为了提供离散化 T2(或者 T3),集合 \{(x,y,z)\in[0,1]^3,x+y+z=1\} 被离散化为 2^2 (或者 3^2)个等边三角形,然后将这些三角形投影到单位球面上,产生第一个八分圆的离散化 \{(x,y,z)\in[0,1]^3,x^2+y^2+z^2=1\}。然后,再通过对称性获得其他七个八分圆的离散化。高阶离散化 T2 \cdot 2^p(或T3 \cdot 2^p )是通过参考集 T2(或T3)的连续优化获得的(您可以在参考文献3-4 中阅读更多关于准均匀正交集的信息)。
对于给定数量的离散方向和简单几何形状(平面边界与轴对齐),满足等式5时,条件正交集 LSE,LSH 和 EWO 的性能要好于几何正交集。对于具有任意取向边界的复杂几何形状,等式5不是所有边界的先验条件。在这种情况下,这些正交集的精度优势可能会丧失,并导致辐射热通量和能量平衡的精度与具有相同数量离散方向的几何生成正交集的精度相当。
几何正交集的主要作用在于可以将它们设计成大量的离散方向(例如,传热模块可以在三维中使用 T8 生成多达 512 个方向,而且很容易生成高阶离散化,例如 T16)。但是,这对计算的要求相当高)。相反的,条件正交集在离散方向上的数量受到限制(如 S12 中使用了 168 个方向;像 S14 这样的高阶离散化是无用的,因为它们的权重为负值,并且产生非物理结果)。
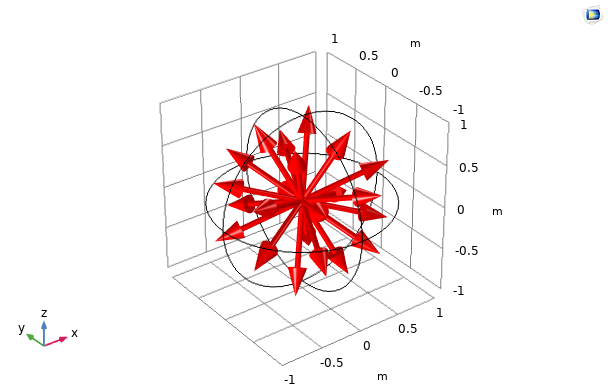
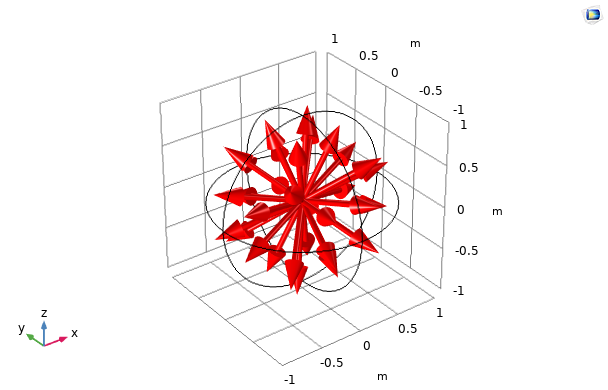
正交集 S2、LSE S4 和 T2 的离散方向 ({\bf s}_i)_{1 \leq i \leq n} 表示如下:
正交集 S2(左),LSE S4(中)和 T2 (右)的离散方向分别在三个维度上具有 8、24 和 32 个方向。
下面,我们将研究离散方向数量的影响。下表两个示例比较了正交集 S2,LSE S6,LSH S6,EWO S6,T3 和 T8 中的二维离散方向数量:
| 正交集 | 离散方向 |
|---|---|
| S2 | 4 |
| LSE S6 | 24 |
| LSH S6 | 24 |
| EWO S6 | 24 |
| T3 | 36 |
| T8 | 256 |
示例1:吸收介质中的辐射
本节,我们以吸收介质中辐射的离散坐标正交集模型为例,吸收介质不会散射或发射能量。辐射传热方程简化为:
并遵守适当的边界条件。
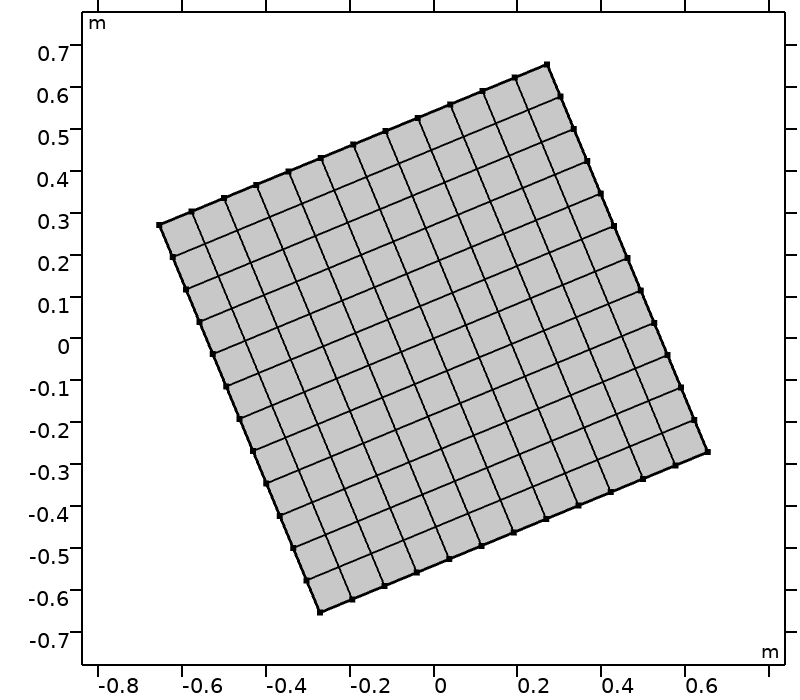
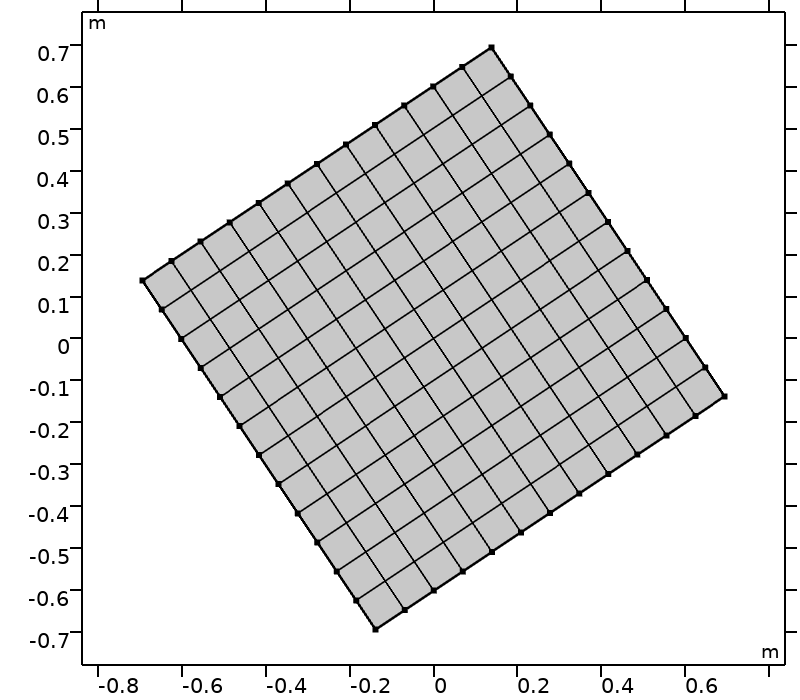
为了评估复杂几何中正交集的表现,需要旋转计算域。计算域 \mathcal{D} (\theta) 是基于参考系 \mathcal{D}(0) = [-0.5,0.5]^2 通过中心点 (0,0) 和角度 \theta 旋转得到,如下图所示。
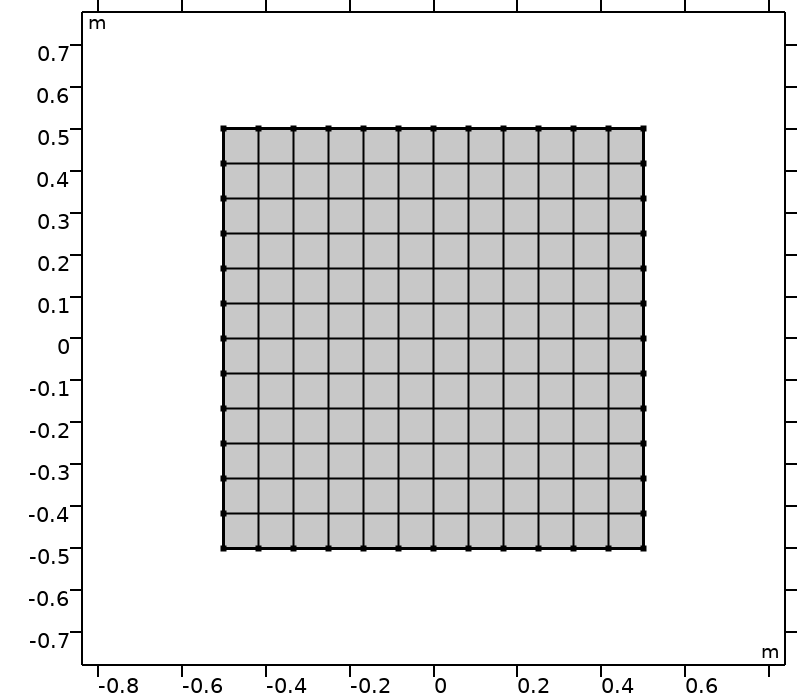 |
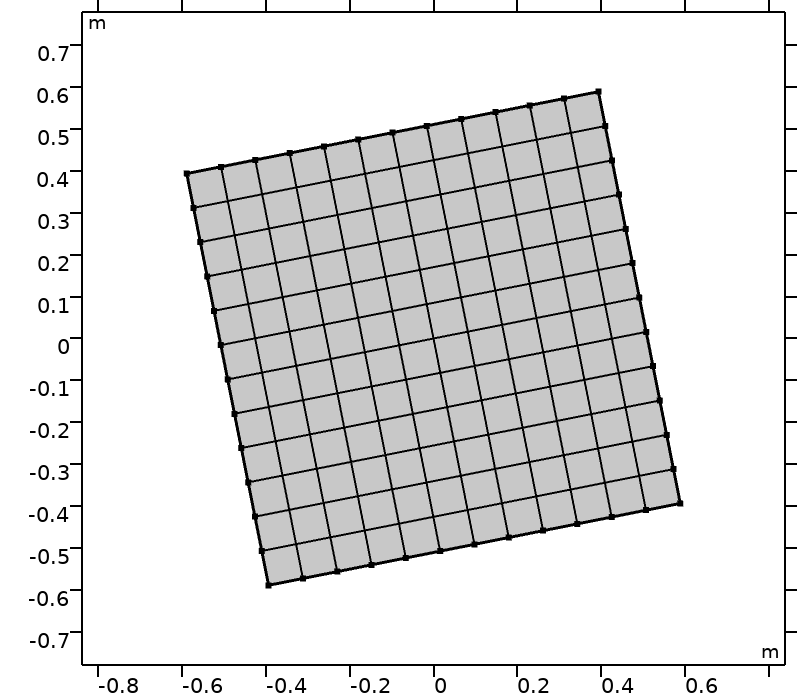 |
 |
 |
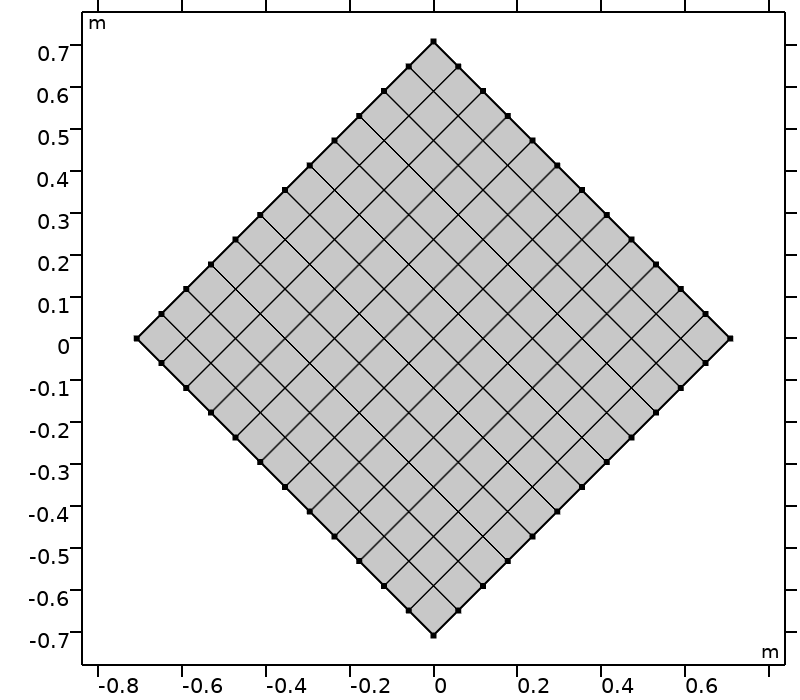 |
计算域 \mathcal{D}(\theta) 和 \theta \in \big \{ k \pi /16, k \in \{0,\ldots,4\}\big \}。
作为边界条件,考虑 \partial \mathcal{D}(\theta) 上的入射强度 I_{\rm w}(I_i=I_{\rm w}, \; {\bf n} \cdot {\bf s}_i < 0, \; i \in \{1,\ldots,n\}),附录中列出了该问题的解析解:能量以指数的形式被吸收。通过入射辐射的数值误差 G_{\rm num} ,与通过离散化 T8 得到的解析解相比,G_{\rm T8} 可以量化为
能量平衡的误差被量化为
式中,Q_{\rm r} 和 {\bf q}_{\rm r} 分别是辐射热源和辐射热通量。
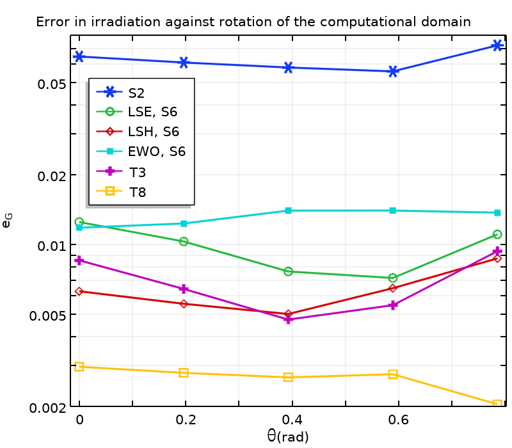
下图列出了在 144 个元素映射域上获得的结果。
不同离散化和旋转的计算域中,平均入射辐射(左)和能量平衡(右)的误差。旋转误差为 \theta_k = k \pi /16, k \in \{0,\ldots,4\}。
正如预期,离散方向的数量越多,入射辐射的数值解越好。对于 S6 的离散化,LSH 优于 LSE 和 EWO。请注意,使用 T3 获得的结果与使用 LSH S6 获得的结果非常接近,但是使用 T3 获得的离散方向数量要大于使用 LSH S6 获得的离散方向数量。这表明对于给定数量的离散方向,条件正交集的表现优于几何正交集。
所有方法均能产生令人满意的能量平衡。请注意,对于此案例,若包含更多数量的离散方向,能量平衡可能会存在缺陷。实际上,某些离散方向几乎与边界共线,并且在那里使用的网格可能不够精细,无法解析这些辐射强度的强梯度,因此也无法解析辐射热通量。当然,可以通过细化网格来降低能量平衡中的误差。在某些情况下,一些能量也会在所有方向上发射和散射,因此可以减弱这种影响。接下来,我们看一下当辐射方程与传热方程耦合时正交集的影响。
示例2:参与介质中的辐射传热
在本节中,将对参与介质中辐射传热的离散坐标正交集案例模型的正交集进行比较,要求解的方程是
\nabla \cdot (-k\nabla T) & = \kappa\left(G-4\pi I_{\rm b}(T)\right), \\
{\bf s}_i \cdot \nabla I_i & = \kappa I_{\rm b}(T)-(\kappa+\sigma_{\rm s}) I_i + \frac{\sigma_{\rm s}}{4\pi}\sum\limits_{j=1}^n \phi({\bf s}_i,{\bf s_j})\omega_j I_j,\; i \in \{1,\ldots,n\},
\end{split}
并遵守适当的边界条件。
计算域与第一个示例中使用的域相同。散射反照率 \sigma_{\rm s}/(\kappa+\sigma_{\rm s}) 设置为 1/2。将相位函数选择为二次各向异性多项式:\phi({\bf s}_i,{\bf s}_j) = 1+ a_1 P_1 ({\bf s}_i\cdot{\bf s}_j)+ a_2 P_2 ({\bf s}_i\cdot{\bf s}_j),(a_1,a_2)=(0.5,0.1),P_p,式中,P_p 是 p 阶勒让德多项式(Legendre polynomial)。归一化相位函数,使得 \int \limits_0^{4\pi} \phi d\Omega = 4\pi。边界是不透明的表面,表面辐射率为 0.5。然后将边界条件应用于温度:
- T_{\rm bottom}\left(X(\theta)\right)=T_0+(T_1-T_0)\exp\left(-\big(X(\theta)/(0.2[{\rm m}])\big)^2\right),X(\theta)=(x+y\tan\theta)/\sqrt{1+\tan^2\theta},是底部边界条件。
- {\bf q}\cdot {\bf n}=h(T-T_0)是顶部边界条件。
- 左右边界热绝缘。
参数 (T_0,T_1,h)=(300 \textrm{ K},400 \textrm{ K},10 \textrm{ W.m}^{-2}.{\rm K}^{-1})。
利用能量平衡中的相对误差对正交集进行定量比较
式中,Q_{\rm r} 为辐射热源,{\bf q} 为热通量。
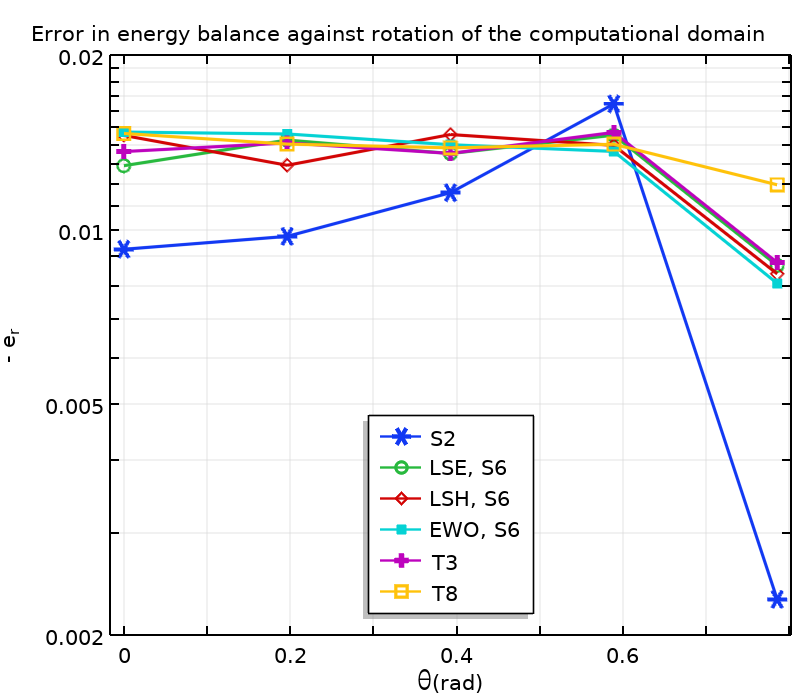
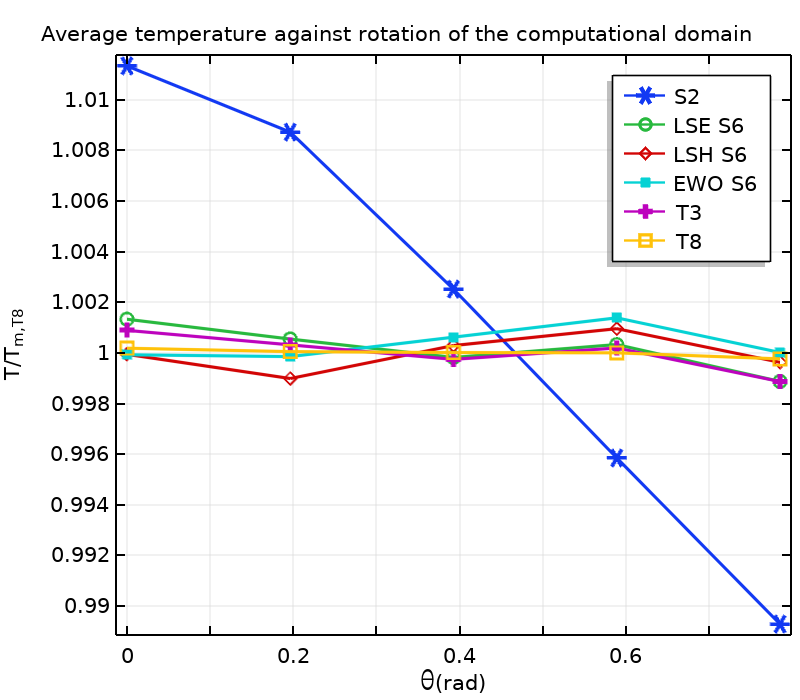
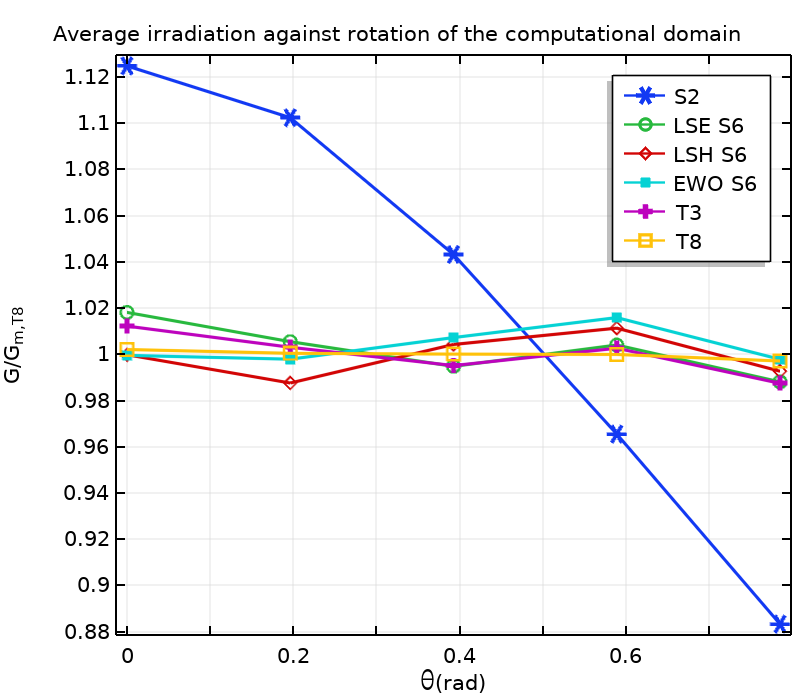
此外,还测试了旋转域对温度和入射辐射场的影响。平均温度、平均入射辐射和能量平衡误差的结果如下所示。下表给出了平均温度和平均辐射的标准偏差。
不同离散化和计算域旋转的能量平衡(左)、平均入射温度(中)和平均入射辐射(右)。当旋转时 \theta_k = k \pi /16, k \in \{0,\ldots,4\},通过 T8 获得的平均温度 T_\textrm{m,T8}=324.03 \ {\rm K} 和入射辐射 G_\textrm{m,T8}=2510.0 \ {\rm W.m^{-2}},对温度和入射辐射无量纲化。
| 标准偏差 | 平均温度 | 平均入射辐射 |
|---|---|---|
| S2 | 2.33 | 197.7 |
| LSE S6 | 0.22 | 21.6 |
| LSH S6 | 0.23 | 22.7 |
| EWO S6 | 0.20 | 18.4 |
| T3 | 0.18 | 17.4 |
| T8 | 0.04 | 3.2 |
平均温度的标准偏差 \sigma(T_{\rm av}) \ {\rm [K]} 以及平均入射辐射 \sigma(G_{\rm av}) \ [{\rm W.m^{-2}}]。
所有方法均均能产生令人满意的能量平衡。S2 的角坐标分辨率不够好,导致相对于旋转计算域而言,入射辐射和温度场的变化很大。由于热量方程和辐射传递方程强耦合,因此这些变化表现出相似的模式。随着离散方向数量的增加,计算结果对域旋转的依赖性降低。对于表中给定的标准偏差,与 LSE 和 LSH 相比,使用 EWO 获得的结果对域旋转的依赖性较小。对于 T3 和 T8,在进一步离散的方向上,标准偏差甚至更低。请注意,除了此处的 T8 之外,能量平衡在很大程度上取决于域的旋转。这可能是由于等式5 不满足 \theta\neq0,当离散方向的数量相当小时(与此处的 T8 相比),会导致边界处的辐射热通量计算不准确。
结语
在本篇博客文章中,我们已经介绍并讨论了 COMSOL Multiphysics® 软件中用于离散坐标方法的正交集。对于给定数量的离散方向,使用 LSE,LSH 和 EWO 之类的条件正交集应比几何正交集效果更好。条件正交集具有有限数量的离散方向。因此,我们感兴趣的的是如何使几何正交集达到更高的角分辨率。
为了进一步想象具有复杂几何形状的模拟,我们还研究了旋转平方计算域对入射辐射、温度和能量平衡的影响。在吸收介质中的辐射计算案例中,与 LSH 和 EWO 相比,使用 LSE 获得的结果对旋转计算域的依赖性更大,但是LSH优于其他条件正交集 EWO 和 LSE,因为它能与分析结果更好地吻合。以参与介质中辐射的热传递为例,离散方向的数量越多,结果对计算域旋转的依赖性越小;但是,对于数量很少的离散方向(本文中测试的所有正交集,T8 除外),结果则依赖于旋转计算域。这是相关的测试在收敛研究离散方向的数量的影响。
尝试对本文介绍的传热示例进行建模:
参考文献
- M.F. Modest, Radiative Heat Transfer, Academic Press, 2003.
- W.A. Fiveland, “The Selection of Discrete Ordinate Quadrature Sets for Anisotropic Scattering,” Fundamentals of Radiation Heat Transfer, vol. 160, pp. 89–96, 1991.
- C.P. Thurgood, A. Pollard, and H.A. Becker, “The TN Quadrature Set for the Discrete Ordinates Method,” Journal of heat transfer, vol. 117, no. 4, pp. 1068–1070, 1995.
- M.A. Badri, P. Jolivet, B. Rousseau, S. Le Corre, H. Digonnet, and Y. Favennec, “Vectorial Finite Elements for Solving the Radiative Transfer Equation,” Journal of Quantitative Spectroscopy and Radiative Transfer, vol. 212, pp. 59–74, 2018.
附录
方程
\begin{cases}
{\bf s}_i \cdot \nabla I_i + \kappa I_i = 0 \textrm{ on }\mathcal{D}(\theta), \\
{\bf n} \cdot {\bf s}_i \textless 0 \Rightarrow I_i = I_{\rm w} \textrm{ on }\partial\mathcal{D}(\theta)
\end{cases}
的解析解是
\forall i \in \{1,\ldots,n\},\forall (x,y)\in \mathcal{D}(\theta), I_i(x,y) & =
\begin{cases}
I_{w}\exp\left(-\alpha \textrm{ if}\left(Y+\tfrac{1}{2}\textgreater r (X+\tfrac{1}{2}),(X+\tfrac{1}{2})S_{X,i}(1+r^2),
(Y+\tfrac{1}{2})S_{Y,i}(1+\tfrac{1}{r^2})\right)\right), & S_{X,i}\geq 0,\;S_{Y,i}\geq 0, \\
I_{w}\exp\left(-\alpha\textrm{ if}\left(Y-\tfrac{1}{2}\textless r(X-\tfrac{1}{2}),(X-\tfrac{1}{2})S_{X,i}(1+r^2),
(Y-\tfrac{1}{2})S_{Y,i}(1+\tfrac{1}{r^2})\right)\right), & S_{X,i}\textless0,\;S_{Y,i}\textless0, \\
I_{w}\exp\left(-\alpha\textrm{ if}\left(Y-\tfrac{1}{2}\textgreater r(X+\tfrac{1}{2}),(Y-\tfrac{1}{2})S_{Y,i}(1+r^2),
(X+\tfrac{1}{2})S_{X,i}(1+\tfrac{1}{r^2})\right)\right), & S_{X,i}\geq 0,\; S_{Y,i}\textless0, \\
I_{w}\exp\left(-\alpha\textrm{ if}\left(Y+\tfrac{1}{2}\textless r(X-\tfrac{1}{2}),(Y+\tfrac{1}{2})S_{Y,i}(1+r^2),
(X-\tfrac{1}{2})S_{X,i}(1+\tfrac{1}{r^2})\right)\right), & S_{X,i}\textless0,\; S_{Y,i}\geq 0,
\end{cases} \\
\alpha & = \frac{\kappa}{S_{X,i}^2+S_{Y,i}^2}, \\
S_{X,i}(\theta) & = s_{x,i}\cos\theta+s_{y,i}\sin\theta, \\
S_{Y,i}(\theta) & = s_{y,i}\cos\theta-s_{x,i}\sin\theta, \\
r & = \frac{S_{Y,i}}{S_{X,i}},\\
X(\theta) & = \frac{x+y\tan\theta}{\sqrt{1+\tan^2\theta}}, \\
Y(\theta) & = \frac{-x\tan\theta+y}{\sqrt{1+\tan^2\theta}}.
\end{split}
符号含义
(a_i)_{1\leq i \leq n},勒让德系数
G,入射辐射[W·m-2]
h,传热系数[Wm-2·K-1]
(I_i)_{1\leq i \leq n},辐射强度[W·m-2·sr-1]
I_{\rm b},黑体辐射强度[W·m-2·sr-1]
I_{\rm w},入射辐射强度[W·m-2·sr-1]
k,导热系数[W·m-1·K-1]
\kappa,吸收系数[m-1]
{\bf n},向外的法向向量[1]
(\omega_i)_{1\leq i \leq n},正交权重[sr]
\Omega,立体角[sr]
(\Delta\Omega_i)_{1\leq i \leq n},离散立体角[sr]
\phi,散射相位函数[1]
\varphi,方位角[rad]
\psi ,极角[rad]
{\bf q},热通量[W·m-2]
{\bf q}_{\rm r} ,辐射热通量[W·m-2]
Q_{\rm r},辐射热源[W·m-3]
{\bf r},位置向量[m]
{\bf s},运输方向[1]
({\bf s}_i)_{1\leq i \leq n},离散方向[1]
\mathcal{S}({\bf r},{\bf s}),散射项[W·m-3]
\sigma(V),变量的标准偏差 V[V]
\sigma_s,散射系数[m-1]
T,温度[K]
\theta,计算域旋转角[rad]



评论 (1)
文举 彭
2020-08-12老师,您好!
学生想咨询一下关于“空间坐标系、材料坐标系、几何坐标系、网格坐标系”之间的区别与关联?麻烦您了,老师!?