在某些应用中,特别是在 MEMS 领域,研究器件特征频率对温度变化的灵敏度非常重要。在本篇博客文章中,我们介绍如何使用 COMSOL Multiphysics® 版本来执行此类研究。我们还探讨了应力软化,几何变化和材料属性的温度依存性等效应。
研究随温度变化的特征频率
一些装置需要对环境变化具有非常高的频率稳定性。最常见的参数是温度,不过湿度变化导致的吸湿膨胀也有可能会引起相同类型的现象。在精度非常高的应用中,频率稳定性可能指定精度为 ppb(十亿分之一,10-9)级别。由于多种现象会相互作用,因此进行精确捕捉这种微小效应的仿真是一项具有挑战性的任务。
矩形梁示例
设想具有以下属性的矩形梁:
| 属性 | 符号 | 值 |
|---|---|---|
| 长度 | L | 10 mm |
| 宽度 | a | 1 mm |
| 高度 | b | 0.5 mm |
| 杨氏模量 | Ë | 100 GPa |
| 泊松比 | ν | 0 |
| 质量密度 | ρ | 1000 kg/m3 |
| 热膨胀系数,x 方向 | αx | 1·10-5 1/K |
| 热膨胀系数,y 方向 | αy | 2·10-5 1/K |
| 热膨胀系数,z 方向 | αz | 3·10-5 1/K |
| 温度变化 | ΔT | 10 K |
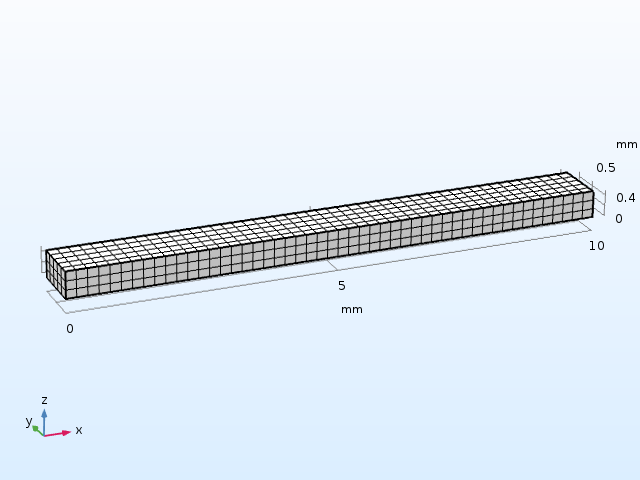
示例中使用的梁几何结构和网格。
材料参数的值与许多其他工程材料的值数量级相同。为了更好地分离各种效应,泊松比被设置为零,但这个假设不会从根本上改变结果。正交各向异性热膨胀系数用于强调解的一些属性。
为了分析热膨胀的影响,我们添加了预应力分析,特征频率 研究。
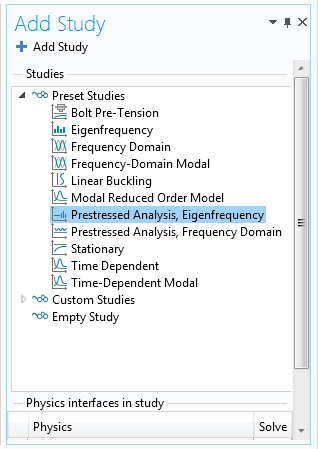
添加 预应力分析,特征频率研究。
该研究包含两个研究步骤:
- 稳态 研究步骤,计算热膨胀引起的位移和应力
- 特征频率 研究步骤,其中需要用到上一步计算的解
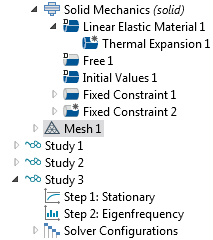
“模型开发器”树中显示的两个研究步骤。
为了计算参考解,您可以添加单独的特征频率 研究或运行相同的研究序列,但不分析热膨胀。
双端固支梁和悬臂梁的特征频率
我们针对两种不同类型的边界条件计算了梁的特征频率:
- 双端固支梁
- 悬臂梁,其一端固定,另一端自由活动
双端固支梁的结果如下所示。
| 模式类型 | 特征频率,Hz | 特征频率,HzΔT = 10K |
比率 |
|---|---|---|---|
| 一阶弯曲,z 方向 | 50713.9 | 50425.1 | 0.9943 |
| 一阶弯曲,y 方向 | 97659.6 | 97526.2 | 0.9986 |
| 一阶扭转 | 266902 | 266917 | 1.00006 |
| 一阶轴向 | 500000 | 500025 | 1.00005 |
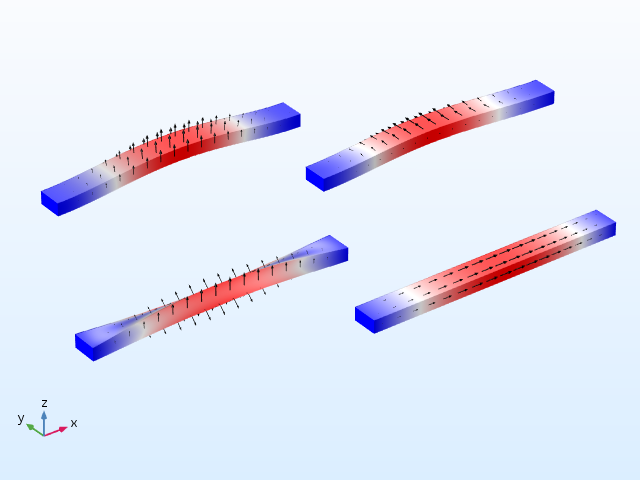
双端固支梁的振型。
下表显示了悬臂梁的结果。
| 模式类型 | 特征频率,Hz | 特征频率,HzΔT = 10K |
比率 |
|---|---|---|---|
| 一阶弯曲,z 方向 | 8063.79 | 8066.92 | 1.00039 |
| 一阶弯曲,y 方向 | 16049.1 | 16053.7 | 1.00028 |
| 一阶扭转 | 132233 | 132265 | 1.00025 |
| 一阶轴向 | 250000 | 250050 | 1.0002 |
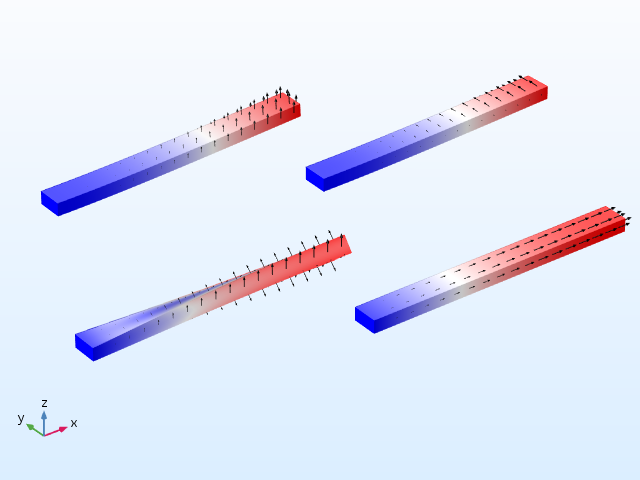
悬臂梁的振型。
首先要注意的是,双端固支梁的弯曲特征模态非常突出,并且具有很强的温度依存性。其中第一阶模态的变化为 0.6%,其他各阶模态的频率相对偏移要小得多。如果将梁变细,这种差异会更加明显。下文将讨论这种现象的原因。
研究应力软化效应
双端固支梁情况由热膨胀引起轴向压应力。根据给定的数据,应力为 -10MPa(通过 EαxΔT 计算)。这种应力导致梁的刚度显著降低,由此产生的效应通常称为应力硬化,原因是它通常发生在具有拉应力的结构中。反过来,压应力使结构软化。
另一种方法是进行线性屈曲分析。您可以通过向模型添加线性屈曲研究并将 ΔT = 10 K 引起的热膨胀用作单位载荷来实现。然后,您将发现临界载荷因子为 80。
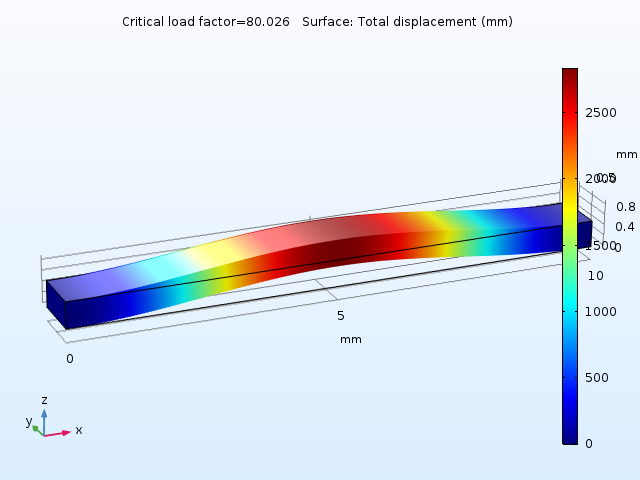
第一阶屈曲模态。
根据线性假设,梁在温度升高 800 K 时变得不稳定。在屈曲载荷下,刚度达到 0。假设刚度随压应力线性降低,则 ΔT = 10 K 时刚度应降低的倍数为
= 0.9875
由于固有频率与刚度的平方根成正比,您可以估算出刚度降低倍数为\sqrt{0.9875}=0.9937,这与计算值 0.9943 基本相符。
应力软化也影响扭转和轴向模态,但效果不如弯曲模态明显。
评估几何变化如何影响频率
悬臂梁受热时不会产生应力,它只会膨胀。在这种情况下,频率偏移仅仅是由几何形状的变化引起的——这种效应远小于应力软化效应。
梁的弯曲,扭转和轴向振动的固有频率对物理属性的依存性如下所示:
f_b \propto \frac{1}
{L^2}
\sqrt{\frac
{EI}
{\rho A}}
f_t \propto \frac{1}
{L} \sqrt{\frac{GK}{\rho J}}
\sqrt{\frac{E}
{\rho}}
这里引入了以下变量:
- I = 弯曲轴周围的面积惯性矩
- G = 剪切模量
- K = 扭转模量
- J = 绕梁轴的极惯性矩
假设梁的初始尺寸为 L0 x a0 x b0,其中 a0 > b0。发生热膨胀后,梁尺寸为 L x a x b。
三个正交方向上的膨胀(应变)分别为 εx、εy 和 εz。本例中,它们与热膨胀成线性关系,εx = αxΔT,εy = αyΔT,εz = αzΔT ; 但原则上它可以是任何类型的非弹性应变。
几何属性的比例为:
(1+\epsilon_y)(1+\epsilon_z)^3 \\\end{align}
(1+\epsilon_z)(1+\epsilon_y)^3 \\\end{align}
F_1(a_0/b_0)(1+\epsilon_y)(1+\epsilon_z)^3 \\\end{align}
\\\end{align}
质量密度也会发生变化。由于相同的质量现在被限制在更大的体中,
\rho = \frac{\rho_0}
{(1+\epsilon_x)(1+\epsilon_y)(1+\epsilon_z)}
通过将这些表达式引入到固有频率的公式,您可以得到以下预期的特征频率偏移:
\frac{f_{b,z}}{f_{b0,z}} = \sqrt{\frac
{(1+\epsilon_y)(1+\epsilon_z)^3}
{(1+\epsilon_x)^3}} \approx 1-\frac{3\epsilon_x}
{2}+\frac{\epsilon_y}{2}
+\frac{3\epsilon_z}
{2}
+\frac{3\epsilon_y}{2}+\frac{\epsilon_z}{2}
\frac{f_a}{f_{a0}} = \sqrt{\frac
{(1+\epsilon_y)(1+\epsilon_z)}
{(1+\epsilon_x)}} \approx 1-\frac{\epsilon_x}
{2}+\frac{\epsilon_y}{2}
+\frac{\epsilon_z}
{2}
由于热膨胀非常小,因此可以认为近似的一阶级数展开是准确的。
对于扭转振动,情况稍微复杂一点,这是因为,a 和 b 的幂在极矩 J 的表达式中是混合的。但是如果您应用这个几何结构中 a = 2b 这个因素,就可以推导出一个类似的表达式。
-\frac{3\epsilon_y}{10}+\frac{6\epsilon_z}{5}
现在,将计算出的频率偏移与悬臂梁的解析预测值进行比较。结果如下表所示,两个结果基本一致。
| 模式类型 | 计算值 | 预测值 |
|---|---|---|
| 一阶弯曲,z 方向 | 1.00039 | 1.00040 |
| 一阶弯曲,y 方向 | 1.00028 | 1.00030 |
| 一阶扭转 | 1.00025 | 1.00025 |
| 一阶轴向 | 1.00020 | 1.00020 |
约束建模的效果分析
当温度升高时,由于横向位移受到约束,梁端部的固定约束会导致局部应力集中。
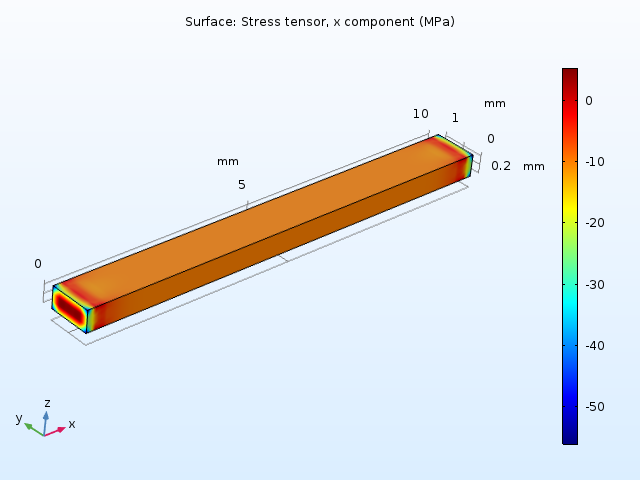
10K 温升引起的双端固支梁轴向应力。
这可能产生两种效应:
- 在预期仅经历体积变化的组件中可能发生应力硬化
- 由于横向位移受到限制(如上例所示),横截面尺寸不再是恒定的
为了确定约束应具有哪些效应,您必须依赖于自己的工程判断经验。通常,组件及其周围环境会受到温度变化的影响。在这种情况下,在 COMSOL Multiphysics 中向约束添加热膨胀的功能就派上用场了。我们看看解是如何受到影响的。
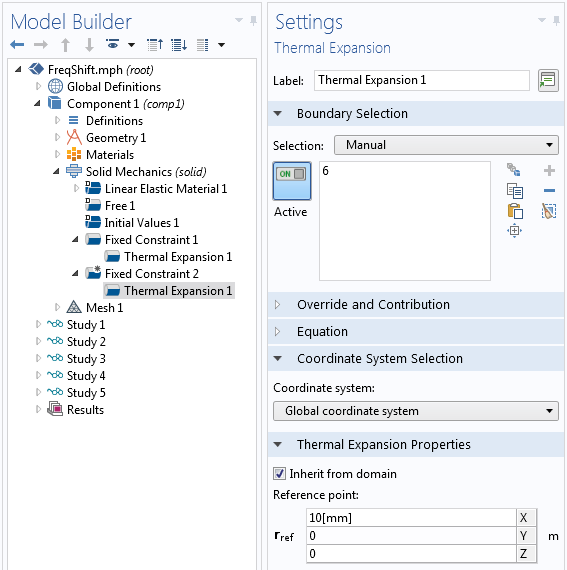
向双端固梁的固定约束添加了热膨胀。
对于悬臂梁,结果发生了变化,现在的结果与解析值完全匹配。
| 模式类型 | 固定约束 | 无应力约束 | 预期值 |
|---|---|---|---|
| 一阶弯曲,z 方向 | 1.00039 | 1.00040 | 1.00040 |
| 一阶弯曲,y 方向 | 1.00028 | 1.00030 | 1.00030 |
| 一阶扭转 | 1.00025 | 1.00026 | 1.00025 |
| 一阶轴向 | 1.00020 | 1.00020 | 1.00020 |
包含材料数据中的温度依存性
在上面的分析中,假设材料数据与温度无关。当分析受约束的结构(主要是应力软化效应)时,这是可接受的近似值。但是,由于几何变化引起的微小频率偏移,我们还必须考虑材料的温度依存性。
在本指南中,您可以看到许多金属的杨氏模量与温度的关系。刚度随温度升高而降低。对于许多材料来说,刚度的相对变化约为 10-4 K-1。这意味着,对于 10 K 的温度变化,预计材料刚度的相对变化大约为 0.1%。这种效应实际上可能大于上面计算的几何效应。
小警告:在测量杨氏模量的温度依存性时,知道由热膨胀引起的几何变化是否被考虑在内是非常重要的。换句话说,您必须知道杨氏模量是相对于原始尺寸还是加热尺寸来测量的。
质量密度的情况就简单多了。在 COMSOL Multiphysics 中执行结构力学分析时,方程在材料坐标系中形成。因此,质量密度不应该有明确的温度依存性,否则就违反了质量守恒定律。
热膨胀系数(CTE)通常随温度升高而增大。相对灵敏度的数量级通常为 10-3 K-1。这个值听起来很大,但从 CTE 代入方程的方式来看,这个值大小并不重要。
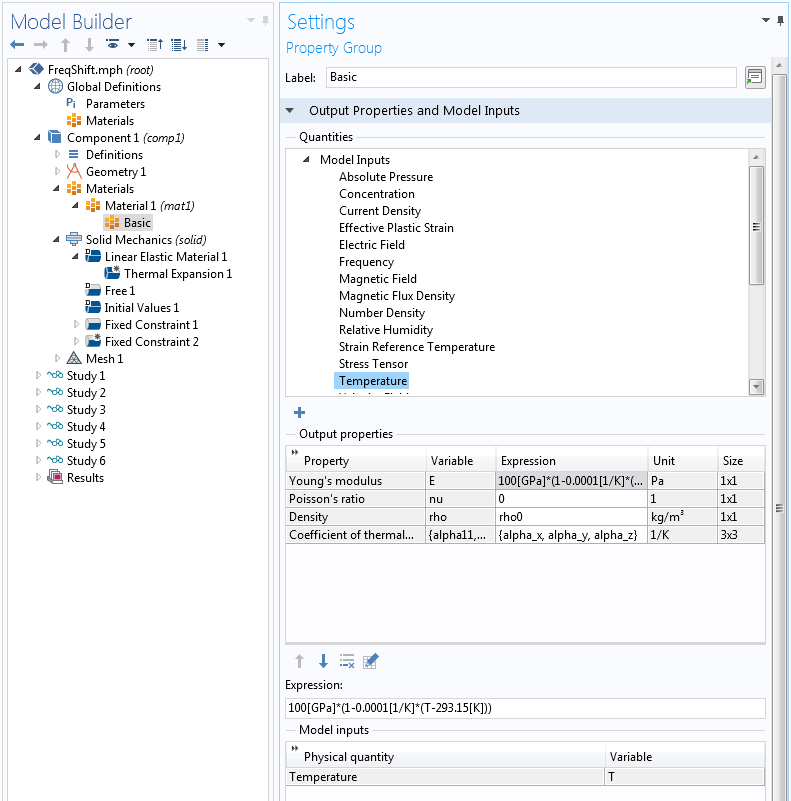
COMSOL Multiphysics “材料库”中的大多数材料都具有温度相关的材料属性。在本例中,您可以通过以下步骤手动将线性温度相关性添加到杨氏模量:
- 在基本 属性组的设置中,选择模型输入 下的温度
- 单击添加 以查看要使用的变量名称 T
- 写出杨氏模量的表达式,它是 T 的函数
您也可以创建一个函数并调用它,以 T 作为变元。
在线弹性材料 的设置中,模型输入 部分现在处于活动状态,您可以提供材料使用的温度。
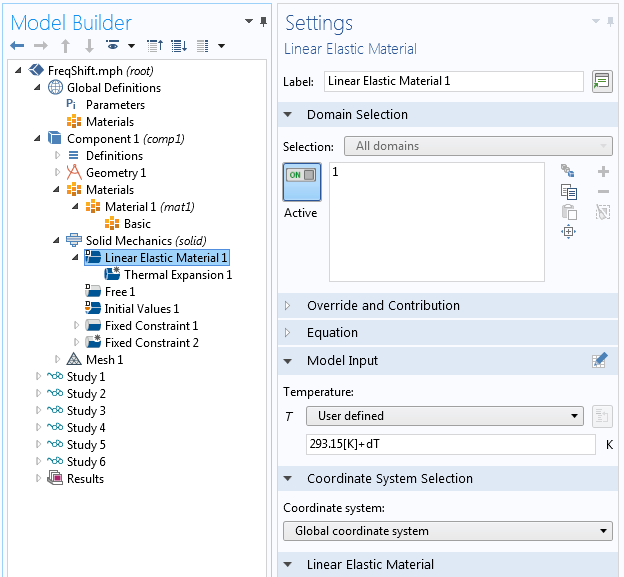
使用 模型输入将温度添加到材料中。
在将杨氏模量减小 1·10-4 K-1 之后,得到的频率偏移变为负值,而不是在杨氏模量恒定的情况下观察到的正偏移(如下表所示)。
| 模式类型 | 无应力约束 常数 E |
无应力约束 温度相关 E |
差值 |
|---|---|---|---|
| 一阶弯曲,z 方向 | 1.00040 | 0.99990 | -0.00050 |
| 一阶弯曲,y 方向 | 1.00030 | 0.99980 | -0.00050 |
| 一阶扭转 | 1.00026 | 0.99976 | -0.00050 |
| 一阶轴向 | 1.00020 | 0.99970 | -0.00050 |
所有模式的位移都与预期完全一致——杨氏模量减小了 1·10-3 倍,固有频率与其平方根成正比。实际上,您可以在频率偏移的线性化表达式中包含杨氏模量的变化,如下所示:
+\frac{6\alpha_z}{5}\frac{\beta}{2} \right)\Delta T
这里,假设 E=E_0(1+\beta \Delta T)。系数 β 的值通常为负值; 在本例中,β = -10-4 K-1。
对于各向同性热膨胀这种常见情况,这些表达式简化为:
+\frac{\beta}{2}
\right)\Delta T
关于数值精度的说明
我们需要 ppm(百万分之一)级别的频率变化。这意味着避免虚假舍入误差非常重要,您可以采取一些措施来确保最佳精度。
在特征频率 节点的设置中,将特征频率搜索基准值 设置为正确数量级的值。
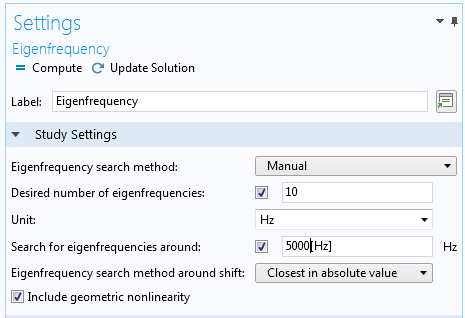
特征频率节点中的更新设置。
然后,减小特征值求解器 节点设置中的相对容差。
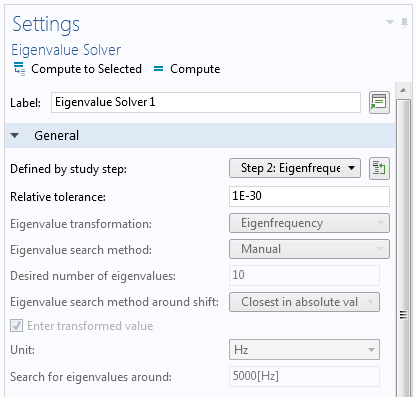
特征值求解器节点设置中减小的 相对容差。
仅更改捕捉物理场所需的参数。例如,对所有研究使用相同的网格。
如果您有理由相信问题是病态问题,例如细长结构的情况,请在直接 求解器的设置中选择迭代细化。
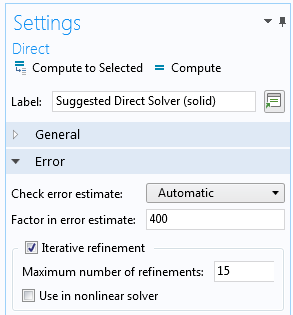
直接求解器的设置,其中显示 迭代细化选项。
几何非线性下处理非弹性应变的理论变化
在 COMSOL Multiphysics® 的 5.3 版本之后,在几何非线性下处理非弹性应变的方法已经改变。当前的默认值是变形梯度的乘法分解,而不是先前版本中使用的应变减法。这是理解为什么现在能够以非常高的精度执行此类分析的一个关键概念。我们来看一种(有点人为的)情况,其中温升为 3·104 K,并且材料属性中没有温度依存性。这意味着伸长率是
因此,体积变化因子为 3.952。
然后,您可以将预应力特征频率分析的结果与尺寸较大(L = 13 mm,a = 1.6 mm,b = 0.95 mm)而密度较低(按体积因子 3.952 进行缩放,ρ = 253.036 kg/m3)的梁的标准特征频率分析结果进行比较。这自然会导致固有频率的大幅增加,原因是,被加热的对象要大得多,但密度却较低。两种方法的频率相对变化如下表所示。
| 模式类型 | 热膨胀与 预应力特征频率 |
几何结构较大、 密度较低 |
|---|---|---|
| 一阶弯曲,z 方向 | 2.2309 | 2.2308 |
| 一阶弯曲,y 方向 | 1.8759 | 1.8759 |
| 一阶扭转 | 1.6702 | 1.6695 |
| 一阶轴向 | 1.5292 | 1.5292 |
从上面可以看出,二者非常一致。扭转模式下存在微小差异,但随着网格的细化,差异逐渐消失。实际上,细化网格表明,最佳预测结果来自预应力特征频率分析。
关于研究随温度变化的特征频率的总结性思考
我们已经讨论了如何使用 COMSOL Multiphysics 精确地确定由温度变化引起的特征频率变化,以及应力软化,几何变化和材料属性的温度依存性等效应。
其他资源
- 阅读以下关于结构力学分析的博客文章:
- 请参阅“发布亮点”页面上的“结构力学模块”更新




评论 (2)
霄砻 简
2022-12-13是否有详细的教程提供呢
hao huang
2022-12-15 COMSOL 员工您好相关案例模型可查看:https://cn.comsol.com/model/eigenfrequency-shifts-caused-by-temperature-changes-49331