如何计算声辐射力

声辐射力是一种重要的非线性声学现象，表现为声场对粒子施加的力总和非零。声辐射是一种声泳现象，是由声音引起的物体运动。我们在之前的一篇博客中讨论的声学粒子悬浮，就是应用声泳力的一个例子。今天，我们将研究声辐射力的本质，并演示如何使用 COMSOL Multiphysics 对其进行计算。

声辐射力及其工作原理

为了理解声辐射力的性质，我们先来看一个简单的例子，即驻波压力场（这里假设是无损的）中的粒子。

当大小有限的粒子受到力的作用后，就会在粒子上产生力的作用，由于压力场存在梯度，因此粒子的一侧比另一侧承受更大的力。但是，如果我们考虑的是一个谐波压力波，那么粒子上的力将表现为谐波函数，可以表示为 F_\text{harmonic}= F_0\sin (2\pi f_0 t+\phi)。在下面的动画中，用黑色箭头表示。

如果将力在时间上求平均，则力的总贡献为零。那么，我们观察到的非零力从何而来呢？

这个问题最早是由 L. V. King 于 1934 年在 On the acoustic radiation pressure on spheres 这篇文章中提出的。为了理解King的结果，我们必须研究声学控制方程是如何推导的。

推导声学方程

作为线性化过程的结果，声学控制方程来自纳维-斯托克斯方程，这个过程通常分两个步骤。

首先，假设在静止的背景场之上，压力和速度的时变扰动非常小。当应用时间导数时，稳态项会消失，仅剩下瞬态扰动项。其余表达式还包含线性和非线性项贡献。后者以两个或多个线性扰动项的乘积的形式出现，它们是由原始纳维-斯托克斯方程中的对流和惯性项产生的。

但是，在最简单的声学限制下，非线性项的贡献可以忽略不计，因为所考虑的扰动幅度非常小。例如，0.01² 远小于 0.01，因此可以忽略不计。在线性化过程的第二步中，忽略所有非线性项，就可以得到线性波动方程。

King 指出，为了理解和计算声辐射力的影响，非线性项必须以某种方式保留在方程中。

方程保留至二阶项，压力场将作为两个项的组合 p = p_1 + p_2 出现，其中 p_1 可以简单的表示为 p_1 = \rho_0 c_0 v，以扰动速度 v 的线性函数出现， p_2 = 1/2 \rho_0 v^2 作为 v 的非线性函数出现。在声学限制下，我们只考虑以下情况：v \ll c_0 ，其中 c_0 是绝热声速，于是得出结论 p_2 \ll p_1。

至此，我们准备回答第一个问题：声辐射力从何而来？

回到驻波压力场中的粒子示例中，我们来研究压力的线性和非线性分量以及这些分量产生的力。在这种情况下，p_1 是一个时谐函数 p_1 = P_1 \cos(kx)\sin(2\pi f t)，p_2 是一个由非线性贡献产生的非谐波函数 p_2 = P_2\cos^2(kx)[1-cos(4\pi f t)]。

这些项可以从上面动画中的波形图中看到。由这些压力项产生的力用箭头表示。线性力（黑色箭头）在幅度和方向上都变化，因此其周期平均贡献为零，而非线性项（红色箭头）仅在幅度上变化，所以平均后得一个非零的力。

计算声辐射力

上述分析简单说明了声辐射力现象的主要原理。直观地讲，如果粒子与周围介质具有相同的声学特性，就不会出现任何力。换句话说，辐射力不仅应该是粒子的尺寸和声场振幅的函数，而且还应该是粒子的声学对比度（粒子的材料特性相对于周围流体的比率）的函数。

由于声学对比，入射在粒子上的场将从它的表面反射，辐射力是入射波和反射波组合的结果。这使得问题很难得到解析解。从 King 开始，一些封闭分析形式的解仅在一些文献中针对某些极限情况给出。他假设刚性球形粒子的尺寸远小于入射波波长，但远大于黏性和热集肤效应。正是第二个假设允许忽略了这些项。

在 On the acoustic radiation pressure on spheres 一文中，King 的结果已经被扩展到包括可压缩粒子。这项研究的结果后来在 1962 年由 L. P. Gor’kov 在 On the forces acting on a small particle in an acoustical field in an ideal fluid 一文中得到证实。当粒子的尺寸与声学边界层（热和黏性）相当时，黏性和热效应变得很重要。M. Settnes 和 H. Bruus 在 2012 年提出了包括黏性的结果。

Gor’kov 开发了一种方法，可以用任何几何形状的静态声场的时间平均动能和势能来表示辐射力。在他的研究中，当对较小的可压缩流体粒子施加力时，可以将力表示为势函数 U_\text{rad} 的梯度表示：

(1)

使用声压和速度表示势函数 U_\text{rad}：

(2)

其中，V_p 是粒子的体积，散射系数由下式给出：

(3)

其中，K_i 是体积模量。散射系数 f_1 和 f_2 分别表示单极子和偶极子系数。这种方法基于散射理论，当 a/\lambda \ll 1 时，只对与小于极限波长 \lambda 的粒子有效，其中 a 是粒子半径。

方程(1)中出现的 v 和 p 项是通过求解线性声学问题获得的一阶项。这种形式的结果通常是使用物理学中广泛使用的扰动方法获得的。在 Henrik Bruus 教授的一本名为 Theoretical Microfluidics 的教科书中，可以找到这种方法应用于声学和微流体的非线性问题的全面介绍和示例。

COMSOL Multiphysics 软件的流体流动颗粒追踪 接口中内置了方程(1)，用于计算粒子上的声辐射力。但是，如上所述，它仅适用于声学上尺寸较小的颗粒，并且忽略了热黏性效应。声学悬浮器模型就是这样一个例子。对利用声辐射现象计算粒子的系统进行建模和仿真时，了解辐射力非常重要。例如，模拟用于分选和处理细胞和其他粒子的微流体系统。博客声流体多物理场问题：微粒声电渗疗法中就讨论了一个这方面的例子。

为了将理论扩展到声学小粒子的限制之外，需要一种数值方法。我们接下来将讨论这种方法。

在 COMSOL Multiphysics 中实现扰动解方法

一般来说，所有力都可以用动量通量表示为 \mathbf F = \int_S T \mathbf{n} d\mathbf{a}，其中积分表面 S 是粒子的外表面。

Gor’kov 利用这一事实获得了作用在任意声场中粒子上的力的封闭解析表达式。为了计算非线性声辐射力，必须对由声场引起的动量通量进行计算，直到二阶项。他的结果的主要吸引力在于，二阶项可以用线性问题的解来表示。

为了实现他的方法，我们需要求解声学问题，使用结果计算二阶动量通量，并将解代入通量积分。

H.Bruus 已经证明，忽略热黏性效应，二阶通量项为：

(4)

这个积分应该是在一个随着施加的力而移动的粒子表面上进行。这意味着积分的表面是时间的函数 S = S(t)。为了解决这个难题，Yosioka 和 Kawasima 表示，可以将积分转化为一个包围粒子的平衡表面 S_0。通过添加一个对流动量通量项来补偿误差，这个力就变成了：

(5)

现在要做的就是求解声学问题，以获得声压和声速，并将它们代入方程(5)的积分中。与方程(1)–方程(3)中使用的方法不同，只要给定应力 T，方程(5)中给出的力表达式对于所有颗粒尺寸都有效。 Southampton 大学的一个研究团队最近在 COMSOL Multiphysics 中使用了这种方法。

应该注意的是，方程(4)中的表达式仅在忽略黏性和热效应时才是正确的。如果包括这些损失，积分表面 S_0 应该在边界层之外，或者在颗粒表面使用正确的全应力 T 表达式。M. J. Herring Jensen 和 H. Bruus 在 2013 年 ICA-ASA 会议上提出了包括热和黏性损失在内的第一性原理扰动方法，题为“First-principle simulation of the acoustic radiation force on microparticles in ultrasonic standing waves”。论文““Numerical study of thermoviscous effects in ultrasound-induced acoustic streaming in microchannels” ，给出了适合在 COMSOL Multiphysics 中实现的二阶以下控制方程的详细推导过程。

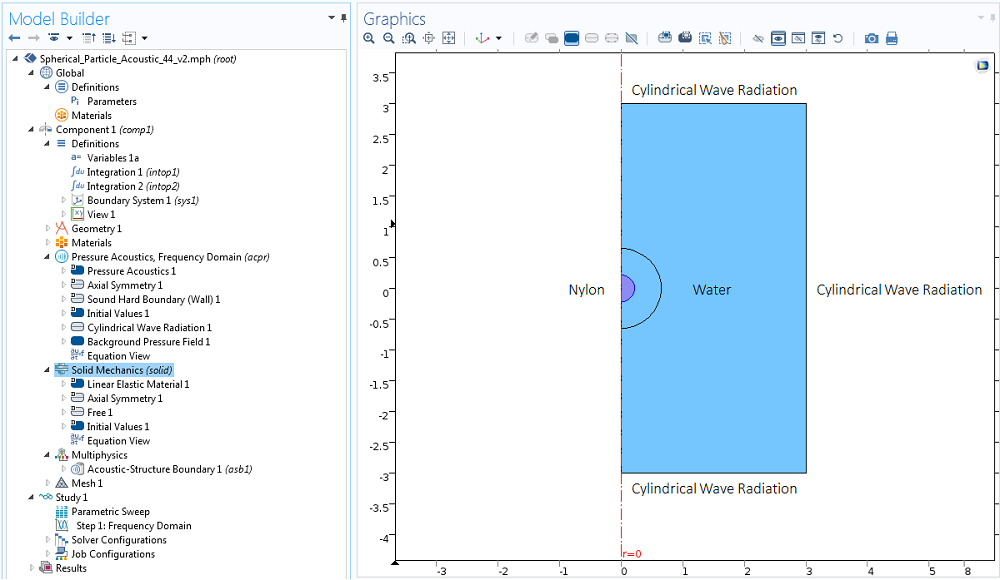
为了对 Glynne-Jones 等人提出的方法进行基准测试，我们来计算驻波对浸入水中的球形尼龙颗粒施加的声辐射力。假设频率为 1 MHz，压力幅度为 1 bar，并使用二维轴对称几何中的声-结构相互作用 接口进行模拟。模型中方框的尺寸为四个波长高和两个波长宽。

使用背景压力场条件在这个方框中激发一个驻波，设置使粒子与压力节点保持一定距离 \lambda/8。

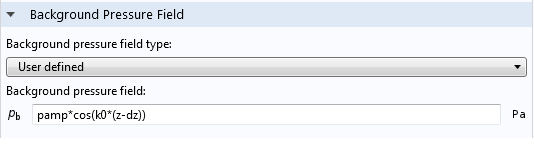
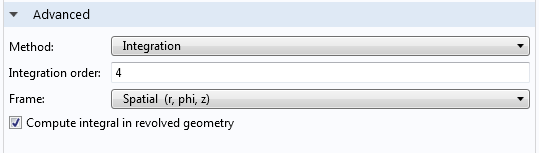
方程(5) 中的积分是通过在组件 1 >定义 节点中设置积分耦合算子来计算的。我们需要确保积分是在回转几何体中计算的，通过选中适当的方框并选择粒子的边界来定义积分表面。

值得一提的是，这种方法中使用的力的计算与积分表面无关，因为它位于粒子外部，所以通量守恒。事实上，使用更远距离的表面在数值上会更加准确，这仅仅是因为会有更多的点可用于积分的数值计算。为了进行这种积分，我们可以在粒子外部添加另一个表面。

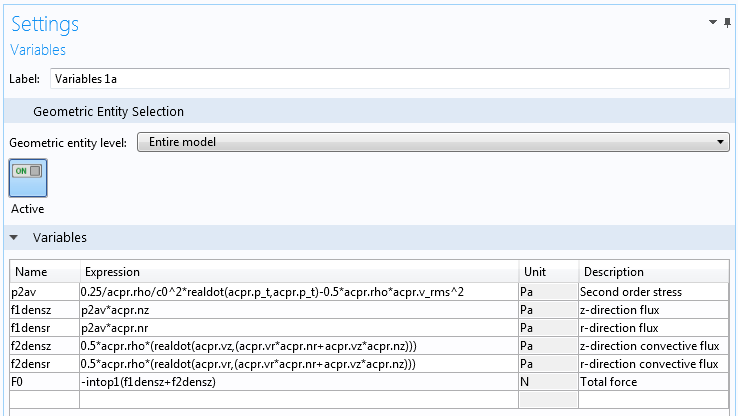
最后，在组件 1 >定义 中引入了新的通量变量作为变量 1a 节点。它们被用作积分算子计算总力的参数。

将结果与解析解进行比较

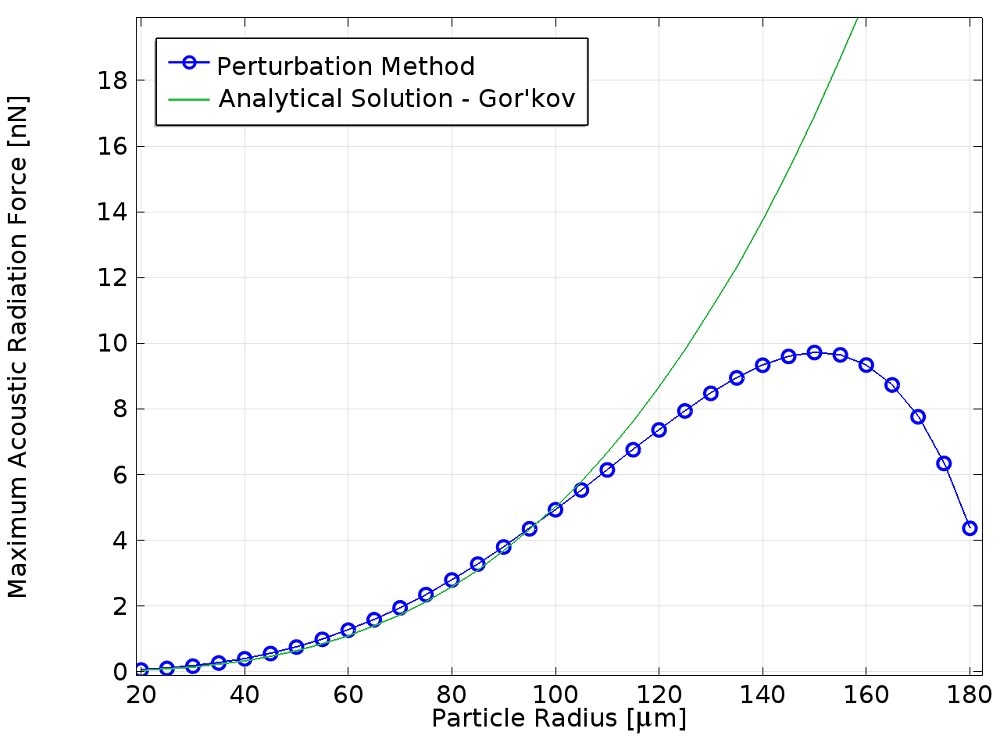
现在，我们来比较扰动方法与解析解方法。

跟我们预期的一样，在解析解成立的小粒子半径范围内，使用两种方法得到的结果具有良好的一致性。一些在散射场分解中包含高谐波的解析模型，对大球形粒子和小球形粒子，均提供了与数值方法曲线趋势一致的解。（例如 T. Hasegawa 的论文，“Comparison of two solutions for acoustic radiation pressure on a sphere”。

对于小粒子半径，解析法和数值方法之间的微小差异可能是因为理论模型假设颗粒是塑性的，而在本例中，我们考虑的是体积模量为 0.4 的弹性粒子。

结束语

扰动方法有许多优点。

首先，它利用了线性声学方法计算非线性二阶力效应，可以将分析轻松地扩展到由任意形状和材料组成的三维粒子。例如，我们可以将它扩展用于模拟生物细胞或微气泡上的声辐射力。

其次，由于声学方程是在频域中求解的，建立了非常有效的数值方法，因此即使在三维模式下，COMSOL Multiphysics 的求解也非常快。

这种方法的缺点是，它是基于一系列简化假设的理论结果，并且只能在有限的情况下进行验证。那么有没有一种可以直接解决问题的数值方法？在下一篇博客中，我们将为您讲解如何实现这一目标。敬请期待！

系列博客中的其他帖子

1. 使用直接流固耦合方法计算声辐射力
2. 声学轨迹角动量仿真

延伸阅读

• 博客文章：
  • 采用声悬浮技术精准制药
  • 热黏性声学的理论基础：热损失和黏性损失声学
  • 声流体多物理场问题：微粒声电渗疗法
• 模型: 声悬浮器
• L. V. King, “On the acoustic radiation pressure on spheres“, (1934)
• M. Settnes and H. Bruus, “Forces acting on a small particle in an acoustical field in a viscous fluid“, Phys. Rev. E 85, 016327 1-12 (2012)
• P. Glynne-Jones, P. P. Mishra, R. J. Boltryk, and M. Hill, “Efficient finite element modeling of radiation forces on elastic particles of arbitrary size and geometry“, J. Acoust. Soc. Am., 133, 1885-93 (2013)
• P.B. Muller, R. Barnkob, M.J.H. Jensen, and H. Bruus, “A numerical study of microparticle acoustophoresis driven by acoustic radiation forces and streaming-induced drag forces“, Lab Chip 12, 4617-4627 (2012)
• P.B. Muller and H. Bruus, “Numerical study of thermoviscous effects in ultrasound-induced acoustic streaming in microchannels“, Phys. Rev. E 90, 043016 1-12 (2014)