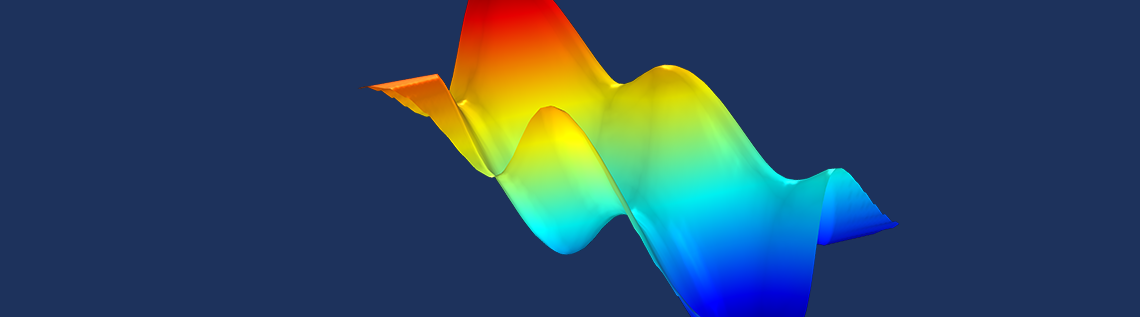
在实际仿真过程中,并不是所有分析都是以 CAD 模型开始的。有时,我们唯一可用的数据仅是一系列点数据,也称为点云数据。在这篇博客中,我们将演示如何将点云数据转换为可在 COMSOL Multiphysics® 软件中进行仿真分析的几何模型。
什么是点云?
点云是指在 x,y 和 z 坐标上绘制的一系列三维点数据。这些点通常来自使用激光扫描仪、测量工具或雷达成像等技术对物体表面进行扫描所获得的信息。
下面的屏幕截图显示了一个文本文件中的部分点云数据,其中的 x,y 和 z 坐标以制表符分隔列的形式排列。
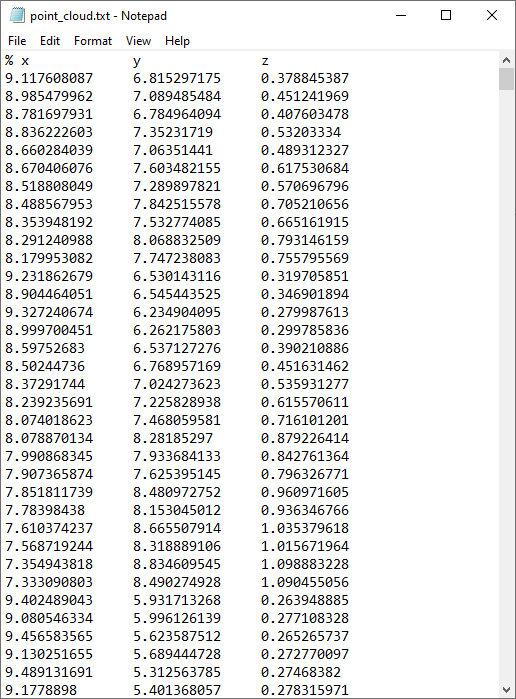
含点云数据的文本文件屏幕截图。
这是 COMSOL Multiphysics 可以导入的最简单的坐标格式类型之一。在软件中,它被称为 电子表格 格式。在这种格式下,可以使用可选的%(百分比)字符来代表注释行。可以用空格、逗号、分号或制表符分隔值和索引。当这类数据被导入后,软件将根据文件中的行号为其指定坐标的索引。由于没有关于这些点之间的信息(也称为连通性),因此这种点集经常存在歧义。我们用一个简单的二维示例来说明可能发生的歧义类型。以下图中的二维曲线为例,从图中可以明显看出,点 5、18 和 7 是曲线上的连续点。
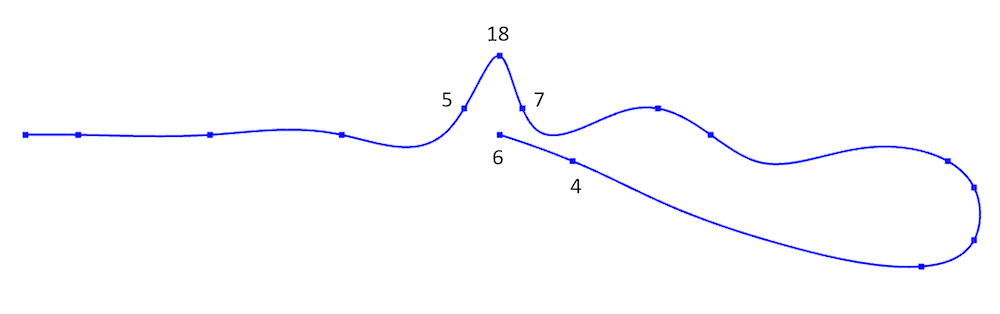
然而,在下图中,由导入的点云数据表示的对应曲线并不是那么明显。也许点 5、6 和 4 是曲线上的连续点?
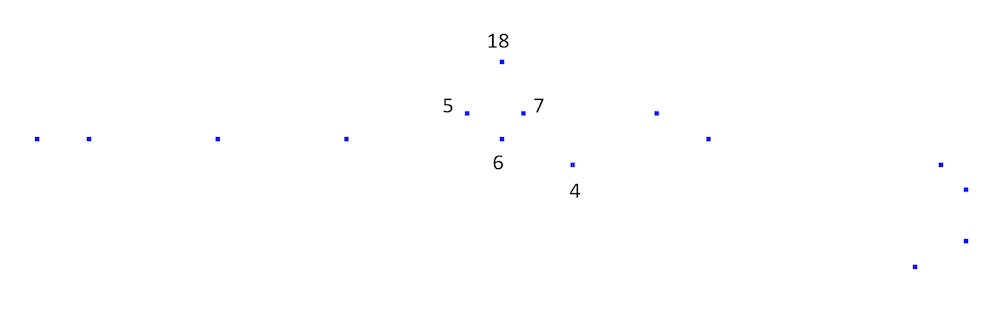
点云数据可能具有内在的歧义。点 5、6 和 4 是不是曲线上连续的点?在这个示例中,它们没有连接,这可以从原始曲线看出,但不能从其相对稀疏的点云数据中看出。
如果一个导入的三维坐标列表带有相关的三角形表面连通性数据,例如 STL,PLY 或 3MF 文件格式,就可以解决这种歧义。比如,一个由两点之间的连通性定义的,并且仅定义了表面的三角形列表。如下所示,三角形表面数据文件
15 17 23
表示将索引为 15、17 和 23 的点作为三角形的顶点相连。
另一方面,如果只有点云数据而没有连通性信息,我们就需要做出其他假设来解决这种歧义。一种可能的假设是:表面数据以 z=f(x,y) 的形式表示,也称为函数面。如果数据不在该表单 z=f(x,y) 上,可以尝试将其分成几部分,使每一部分在表单 z=f(x,y) 上。这里要注意的是,在表单 y=f(x,z) 或者 x=f(y,z) 上的数据在重新排列后同样有用。
可视化点云数据
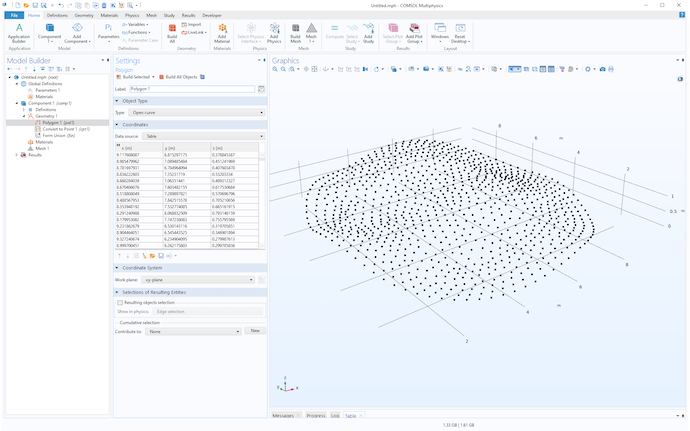
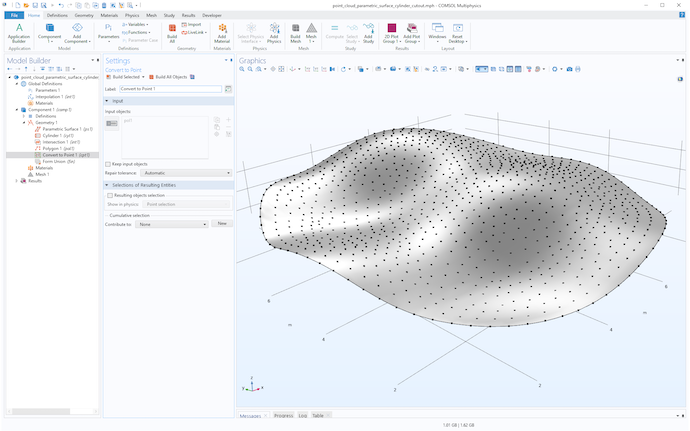
将点坐标数据可视化的一种简单方法是将其作为表格导入到 多边形 几何对象中,然后使用 转换为点 操作,如下图所示。
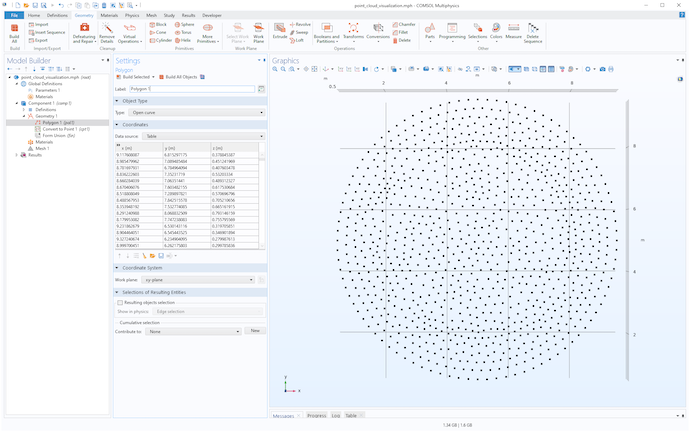
点云数据的可视化图,从两个不同的视角看到的几何点对象。
基于这个视图,可以假设点云数据定义了以 z=f(x,y) 形式表示的函数面。为了方便以后使用,我们需要知道点云的范围。获取此信息的一种简单方法是右键单击几何 节点,然后选择 测量 。
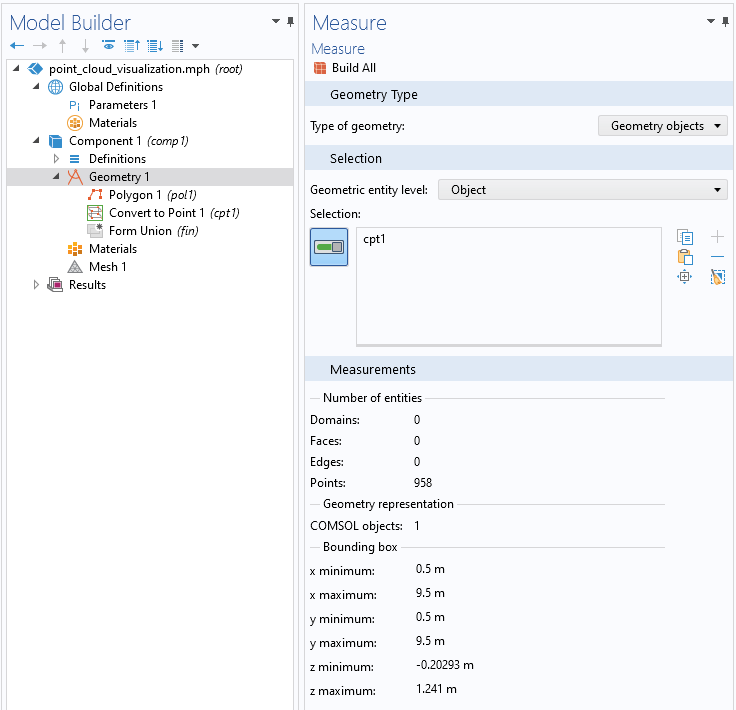
测量设置窗口给出了有关点云范围的信息。
由点云范围显示的信息可以看到,有 958 个点在 x 和 y 方向上都从 0.5 延伸到 9.5m,在 z 方向上从 -0.2 延伸到 +1.5m。本示例中使用的单位是米(m)。
现在,我们可以尝试使用 转换为曲面 操作将这组点数据转换为曲面。但是,这个操作不起作用。因为我们没有这些点的连接信息,所以系统将提示一条错误消息。我们需要以某种方式构建连接性数据。另外,还需要假设数据在表单 z=f(x,y)上。解决方案是将点云作为一个非结构化插值曲面导入。
创建一个插值曲面
接下来,我们在 全局定义 节点下添加一个 插值 函数,并将 数据源 设置为 文件。浏览点云文本文件,在本示例中为 C:\ COMSOL \ point_cloud.txt,如下图所示。您可以点击文章末尾的链接下载此文件。
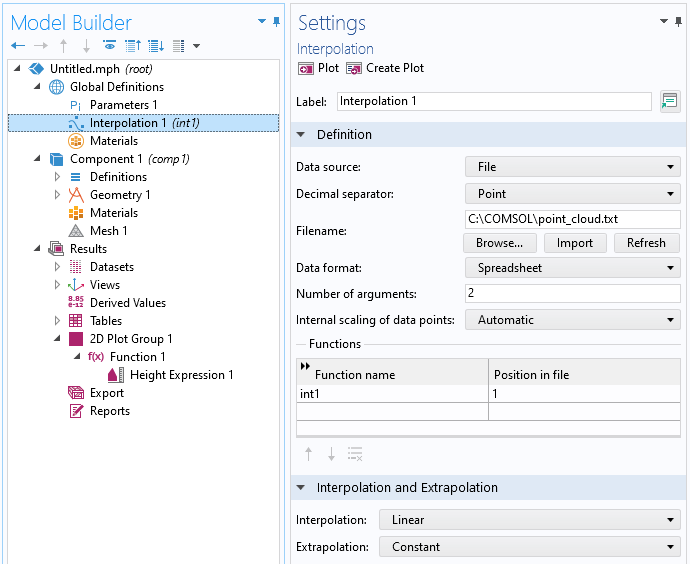
由点云定义的 插值 函数。
该 插值 功能将自动猜测该数据在表单 z=f(x,y) 上,文件的前两列分别代表 x 和 y 坐标,第三列代表函数值,即函数曲面的 z 坐标。我们可以从参数量中看到这一点,它被自动设置为2,分别对应于 x 和 y 坐标。函数名称 被自动设置为 int1(可以更改以及 文件中的位置 被设置为 1 表示int1(x,y)的函数值,代表 z 坐标的将由输入参数列之后的第一列给出。换句话说,列数 2+1=3。在这个示例中,文件只有三列,因此 1 是唯一选择。如果数据采用其他形式,则可以在导入之前使用文本编辑器或电子表格软件(例如 Excel®)重新排列数据。
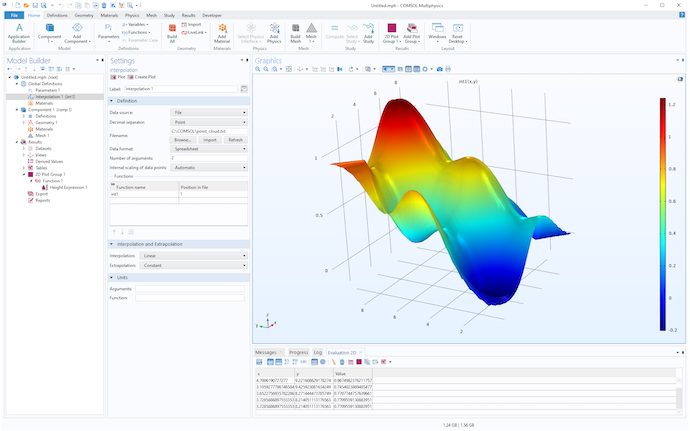
然后,单击 插值设置窗口顶部的 绘图 或 创建绘图 按钮将插值函数可视化。绘图 选项将创建一个临时的可视化结果,创建绘图 选项将创建一个二维 网格 数据集,并在 结果 下的 二维绘图组 节点创建相关的 函数 绘图。
在 结果 及其相关的 设置窗口下以 函数 绘图的形式显示的插值函数。
那么,软件是如何仅基于假设 z=f(x,y) 来创建表面的几何表示呢?首先,插值函数在后台创建 x 和 y 坐标的二维三角形网格,然后将函数值关联到每个点,最后在两个函数值之间进行线性插值。我们可以将这个过程看作在点云上放置一个渔网。请注意,这个三角形网格对用户不可见。在 插值和外推 部分的 插值设置 窗口中,可以看到设置 插值选项,它默认设置为 线性。另一个选项是 最近邻插值,它将创建一个分段常数函数插值,在这个示例中没有用。
这部分的另外一个设置是 外推。这个功能用于猜测函数定义范围之外的值,定义范围由 x 和 y 坐标确定。在这个示例中,点云分布在 xy平面的一个圆内。当将数据可视化为 函数 图时,xy 数据取自一个矩形 二维栅格 数据集,并且插值函数将以辐射模式分配常数函数值,用于填充圆和矩形之间的空间,以限制点云数据。如下图所示,我们可以从点云数据中识别出圆形迹线。
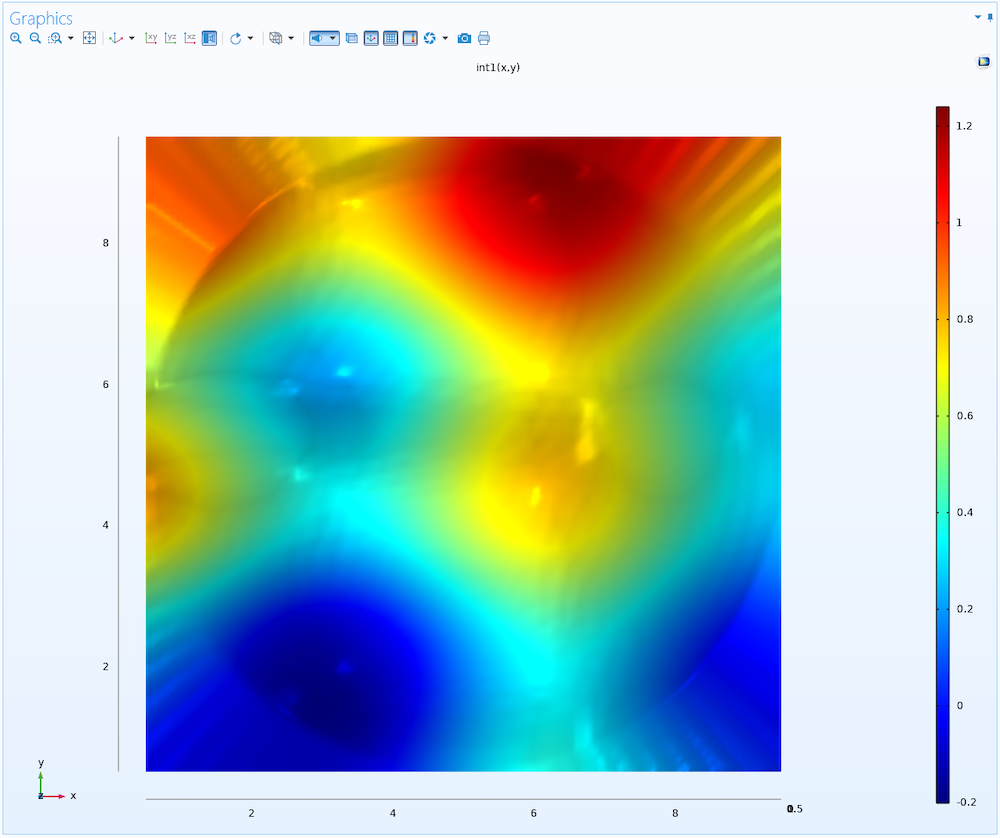
内插函数的俯视图,在定义原始点云迹线的圆形区域之外可以看到外推部分。
软件又是如何将这个插值函数转换为可以进行网格划分和仿真分析的几何表示呢?这是通过使用 参数化曲面 几何对象完成的,我们将在后面进行介绍。
创建一个参数化曲面
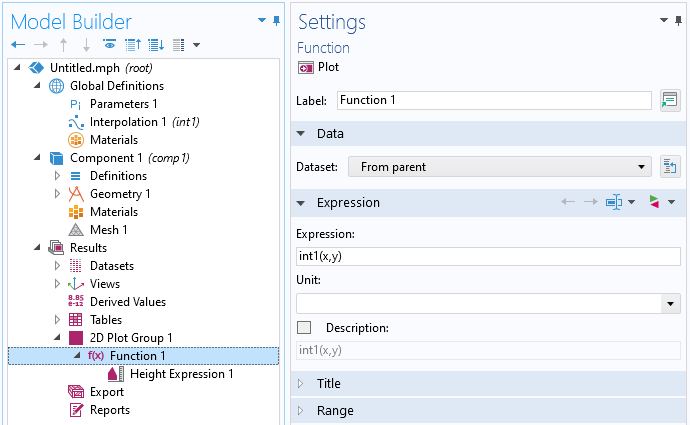
要创建一个基于上述插值函数的 几何表面,请根据下图在 几何 下添加 参数化曲面 特征。
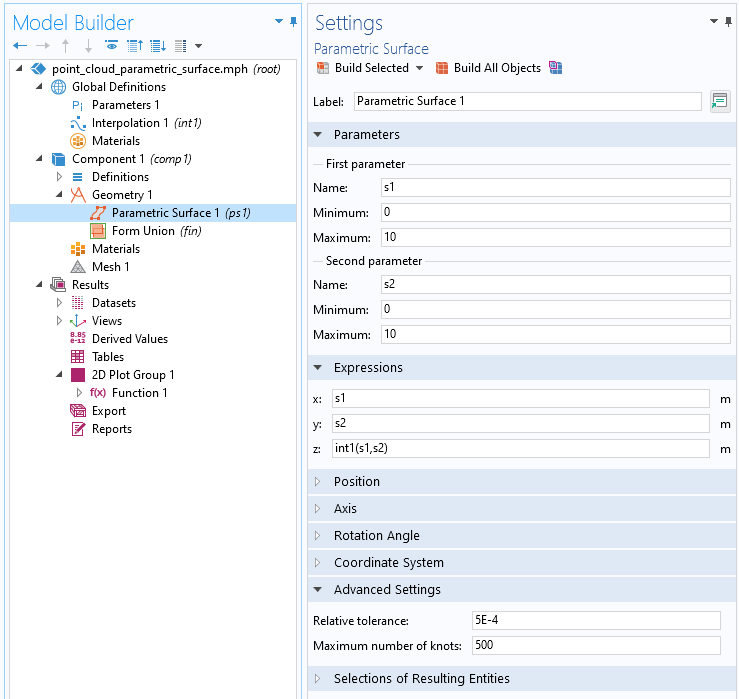
基于点云插值函数的表面的 参数化曲面 设置。
在这个 设置 窗口中,s1 和 s2 分别被解释为 x 和 y 坐标,int1(s1,s2)解释为 z 坐标。现在,我们需要使用之前通过 测量 工具获得的信息。我们将 s1 和 s2 的最小值和最大值设置为比点云数据的测量范围宽一点,以确保不会遗漏任何细节。
在这个示例中,参数化曲面 将在两个方向上被定义在 0 到 10 之间,以与测得的 0.5 到 9.5 之间的点云数据进行比较。
在内部,COMSOL 软件用 B 样条表面表示参数化曲面,该 B 样条曲线表面近似于计算以 x,y 和 z 表达式 定义的数学表面。 B 样条曲面是分段多项式曲面,所使用的分段多项式的数量由 结 数间接确定。结数越大,分段多项式的数目越多,近似效果越好,但是计算成本更高。B 样条曲面中的结数会自动增加,直到曲面近似值满足 相对容差 栏中指定的 容差 或直到达到 相对容差 栏中 最大结数 栏指定的结数为止。根据相对于参数化曲面的边界框的空间对角线测量容差。
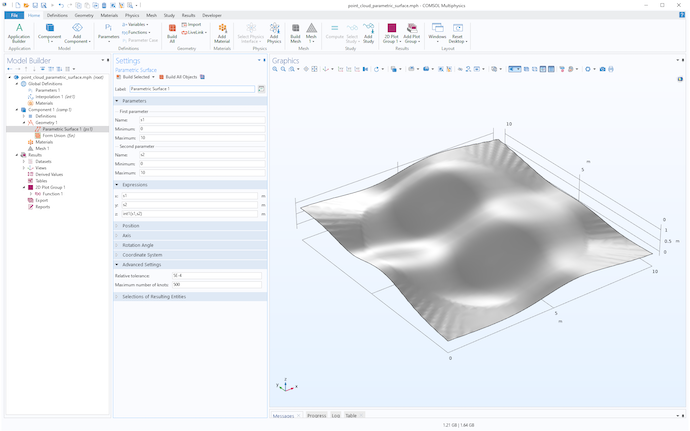
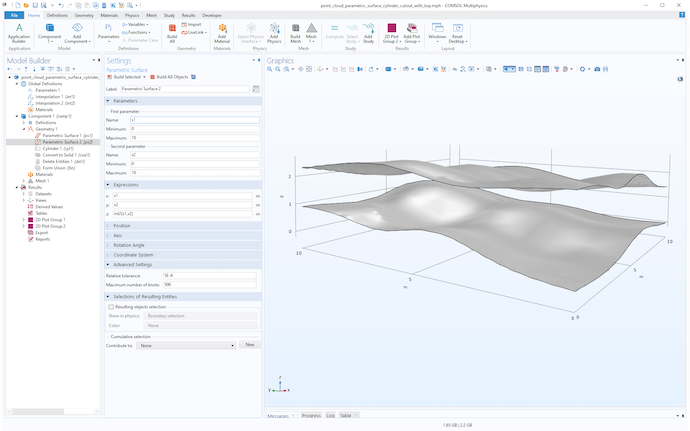
在这个示例中,我们使用试错法得到 相对容差 为 5e-4,而 最大结数为 500。(默认值分别为 1e-5 和 20。)下图显示了生成的曲面。
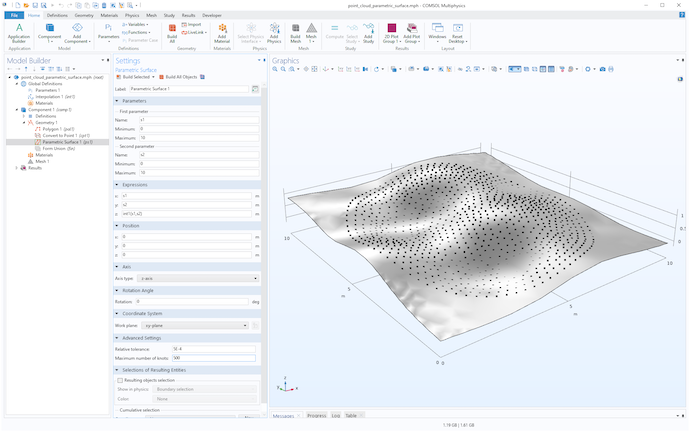
我们可以在更早的时候就使用这项技术,以同时可视化点云和曲面,如下图所示。
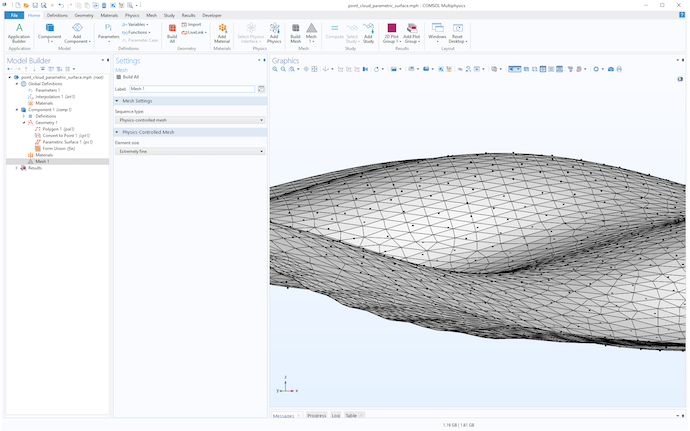
要更好地控制表面可视化的细节,可以单击 网格 节点并创建适当 单元大小 的网格。下图显示了使用 极细化 设置的网格。要获得更高的分辨率,请选择 用户控制网格 选项并设置 定制 单元大小。
修剪表面
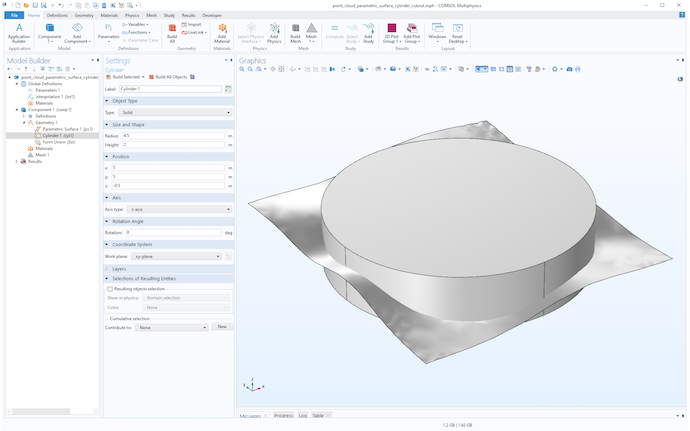
在原始点云数据中心有一个圆心在x=5,y=5上,半径为 4.5 的圆形迹线。下图显示了添加一个圆柱体来拟合这些测量点,圆柱体高度位于 z 方向的最小值和最大值之间。
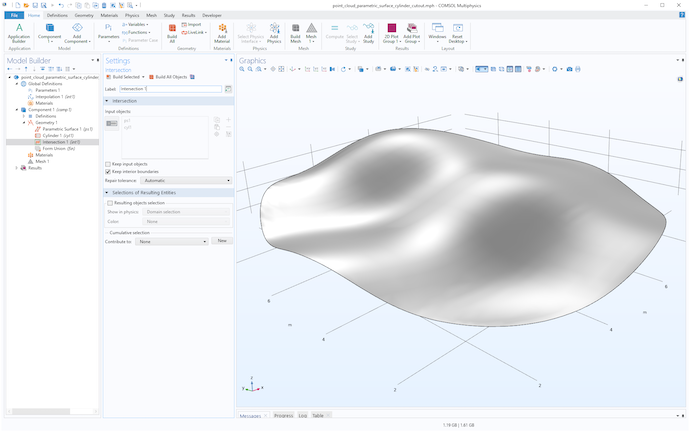
现在,使用 交集 操作通过选择曲面和圆柱体来修剪表面,如下图所示。
在两个曲面之间的空间创建实体
要在两个内插曲面之间的空间创建具有圆形迹线的实体,只需重复上述步骤导入第二个曲面即可,如下图所示。
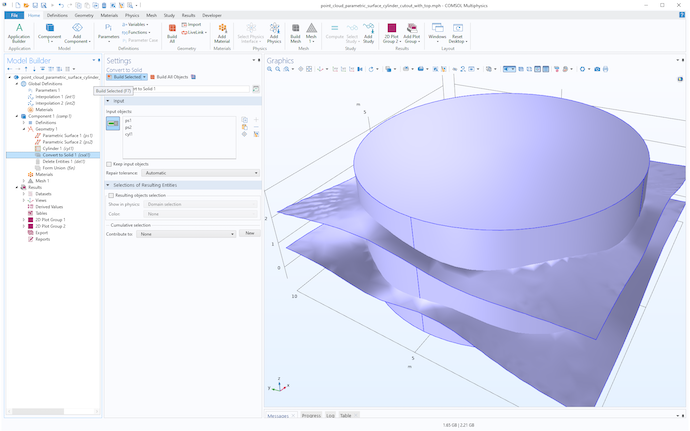
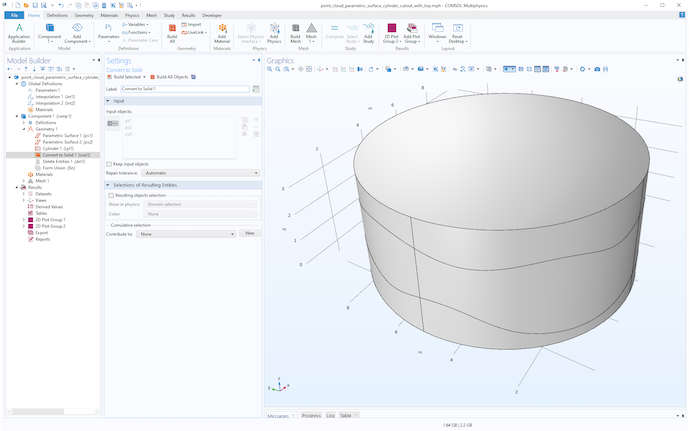
然后,创建一个圆柱体来修剪表面,并对所有对象使用 转换为实体 操作,如下图所示。
使用圆柱体修剪两个表面。
我们可以使用 分割对象 或 分割域 操作获得相同的结果。这些操作比 转换为实体 更复杂,并且允许选择圆柱作为要分割的对象或域。然后,可以选择插值曲面作为用于分割的工具对象。在某些情况下,分割域 操作适用性更广,因为它允许从对象中分割选定的域,并且可以选择自动扩展平面、圆柱或球形工具面,当这些平面与要划分的域不相交时。
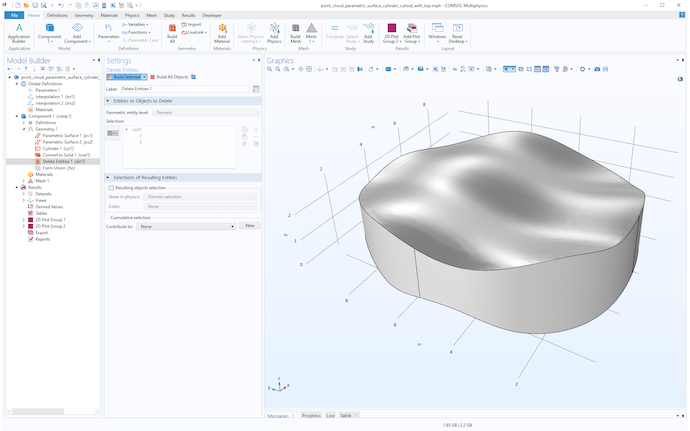
最后,使用 删除实体 删除不需要的域,如下图所示。
现在可以对该实体进行网格剖分,并用于任何类型的仿真。在这种情况下,我们可以创建仅有六面体的扫掠网格,如下图所示。
生成点云数据进行测试
我们可以通过本页底部的链接下载本博客文章中使用的点云数据和文件。如果想生成自己的点云数据,使用任何表面。在下图中,如上例所示,使用了一个参数化曲面,并用圆柱体对其进行了修剪,用于 z 坐标的表达式为:
z = 0.25 * cos(s1)+ 0.2 * cos(1.5 * s2)* exp(-0.1 * s1 + 0.1 * 0.25 * s2)+ 0.1 * s2
实际上,这是用于生成第一个示例中使用的点云数据的表面。
现在,创建一个网格,然后右键单击 网格 节点并选择 绘图 在结果 下生成一个网格图。接下来,右键单击 网格图>网格,然后选择添加要导出的绘图数据 。在数据的设置窗口中,将1用作表达式。由此导出的常量值将不被使用。选择一个文件名,然后单击窗口顶部的导出 将数据写入文件。
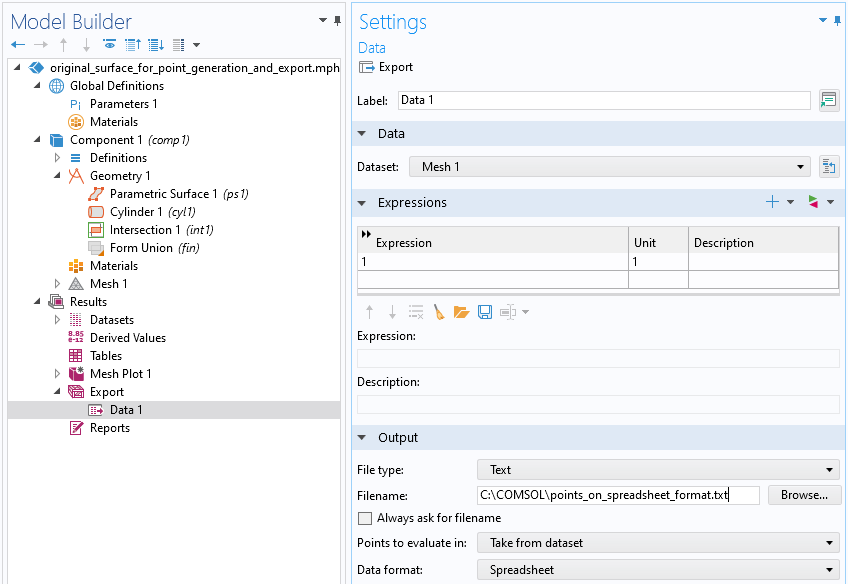
用于以电子表格格式输出数据的输出设置。
如果在文本编辑器或电子表格软件中打开生成的文本文件,则会看到带有注释行和四列的标题。最后一列包含常量表达式1。
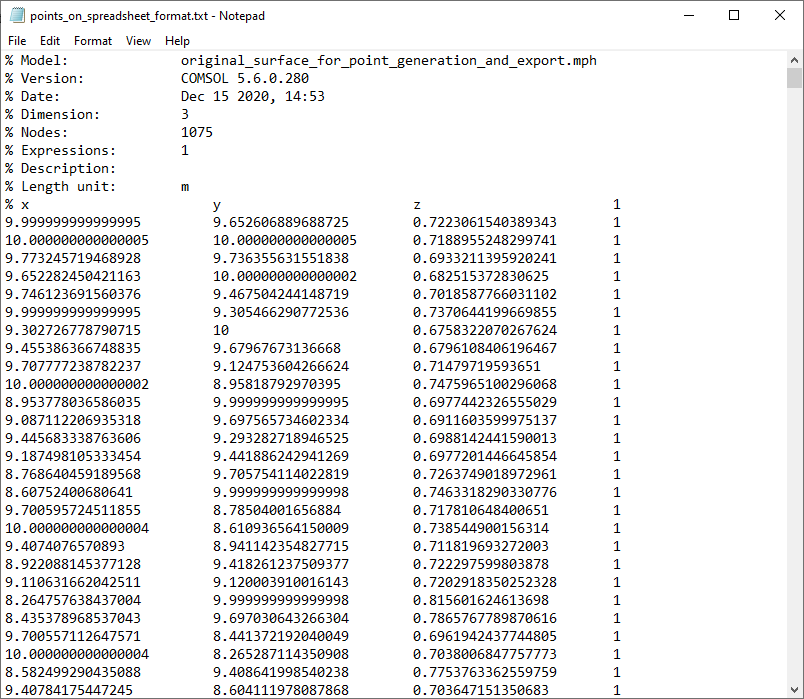
在电子表格软件(例如 Excel®)中,我们可以删除第 4 列,然后将文件再次保存为文本文件格式。生成的文件将采用与前面讨论的示例相同的格式。请注意,标题中的前导注释行是可选择项,可以删除。
结束语
这篇博客介绍的技术可用于多种用途。例如,可以导入两个以上的曲面来创建更加复杂的结构;可以使用非圆柱体对象修剪数据;在其他示例中,点云数据可以基于圆柱或球形坐标;可以将以上技术与坐标转换结合使用以生成圆柱或球形面切片。
有关在岩土工程应用中使用插值数据的真实示例,请参阅这篇博客:将地质模型整合到区域尺度的地下水模型中。
更多相关示例,请参阅这篇博客:如何基于高程数据模拟不规则形状并构建模型几何。
动手尝试:转换点云数据
单击下面的按钮,您可以下载文中使用示例的 MPH 文件和数据文件。您还可以找到一个 MPH 文件,这个文件演示了如何将表达式定义的原始参数平面与点云定义的参数平面进行比较。
Microsoft 和 Excel 是 Microsoft Corporation 在美国和/或其他国家的注册商标或商标。



评论 (0)