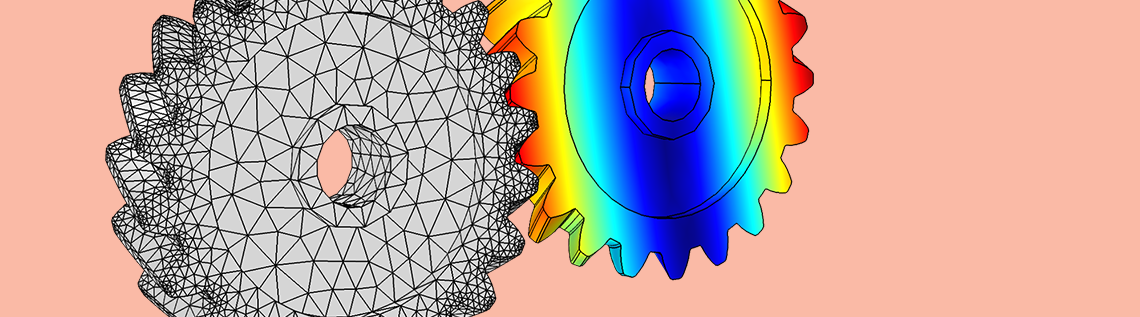
在对传动系统进行噪声、振动和粗糙度(NVH)分析时,齿轮啮合的弹性对结果起着至关重要的作用。COMSOL Multiphysics® 软件中的新特征和功能能够准确地评估齿轮啮合刚度,从而可以帮助我们创建一个精确的齿轮模型。今天,我们将解释为什么要考虑齿轮啮合弹性,以及如何计算齿轮啮合刚度并将其纳入多体动力学模型中的重要性。
齿轮啮合刚度的重要性
在齿轮发明之前,轮子在摩擦力的作用下将一个轴的旋转传递到另一个轴上。使用这种摩擦轮的主要缺点是超过一定的扭矩值时会发送滑脱,这是因为可以传递的最大扭矩会受到摩擦扭矩的限制。为了克服这一限制,人们开始使用齿轮,如今更普遍是被称为钝齿轮或齿轮。

使用多体动力学模块中的零件库创建的齿轮对。
齿轮的主要目的是避免滑移。这就是为什么一个齿轮的齿要插入配对齿轮的齿之间的原因,这个过程称为齿轮啮合。与齿轮的核心区域相比,齿轮的啮合区域更加灵活。因此,当试图准确捕捉系统中的动力学和振动时,考虑齿轮啮合的刚度很重要。
齿轮啮合刚度取决于几个不同的参数,最重要的是,它会随齿轮的旋转而变化。这使得问题变成非线性问题,并且连续变化的齿轮啮合刚度会引起系统的振动。这种存在于传动系统中不同部分的振动会产生噪声辐射。因此,评估齿轮啮合刚度并将其纳入齿轮模型中至关重要。
使用静态接触分析评估齿轮啮合刚度
为了检查齿轮啮合刚度,我们首先假设齿轮是弹性体,并建立它们之间的接触模型。然后进行静态参数分析,以确定啮合循环中不同位置的齿轮啮合刚度。啮合周期的定义是齿轮旋转的圈数,之后下一个齿占据第一个齿的位置。
为了理解这个过程,我们以其中两个均由钢制成的齿轮为例来说明,这些齿轮具有以下特性:
| 属性 | 副齿轮 | 齿轮 | |
|---|---|---|---|
| 齿数 | n | 20 | 30 |
| 中径 | dp | 50mm | 75mm |
| 压力角 | a | 25° | 25° |
| 齿轮宽度 | wg | 10mm | 10mm |
在该示例中,两个齿轮在其各自的中心处铰接。使用罚接触方法,对两个齿轮的齿之间的接触进行建模。相互接触的两个齿轮的边界如下所示。有关如何设置此模型的更多详细信息,可以查看 COMSOL 案例库中的复合轮系的振动模型案例教程。


齿轮副中的接触副边界(左)和有限元网格(右)。
由于啮合周期中齿轮在不同位置的啮合刚度会发生变化,因此我们对两个齿轮进行参数化旋转以计算齿轮啮合刚度的变化。指定副齿轮(θp)绕平面外的轴旋转两个啮合周期。齿轮绕(θw)平面外的轴旋转的定义如下:
其中,齿轮比 gr 为 1.5,θt 的扭转值为 0.5°。
给定齿轮一个扭转角度 θt,和所需的的扭矩 T,并在铰接处进行计算。因此,齿轮副的扭转刚度被定义为:
一旦知道了扭转刚度,就可以将沿作用线的刚度定义为:
其中,dpw 是轮的中径,α 是压力角。
啮合周期中不同位置的齿轮对中的 von Mises 应力分布。这表明沿作用线的接触点处的应力水平很高。
下图显示了在两个啮合周期中,计算出的齿轮啮合刚度随副齿轮旋转的变化。我们可以看到,齿轮啮合刚度在每个啮合周期以及多个啮合周期内都是周期性的,在开始时先增大,之后再减小。这是由于重合度的变化导致的。在啮合周期开始时,重合度从 1 增加到 2,但随后又下降到 1。
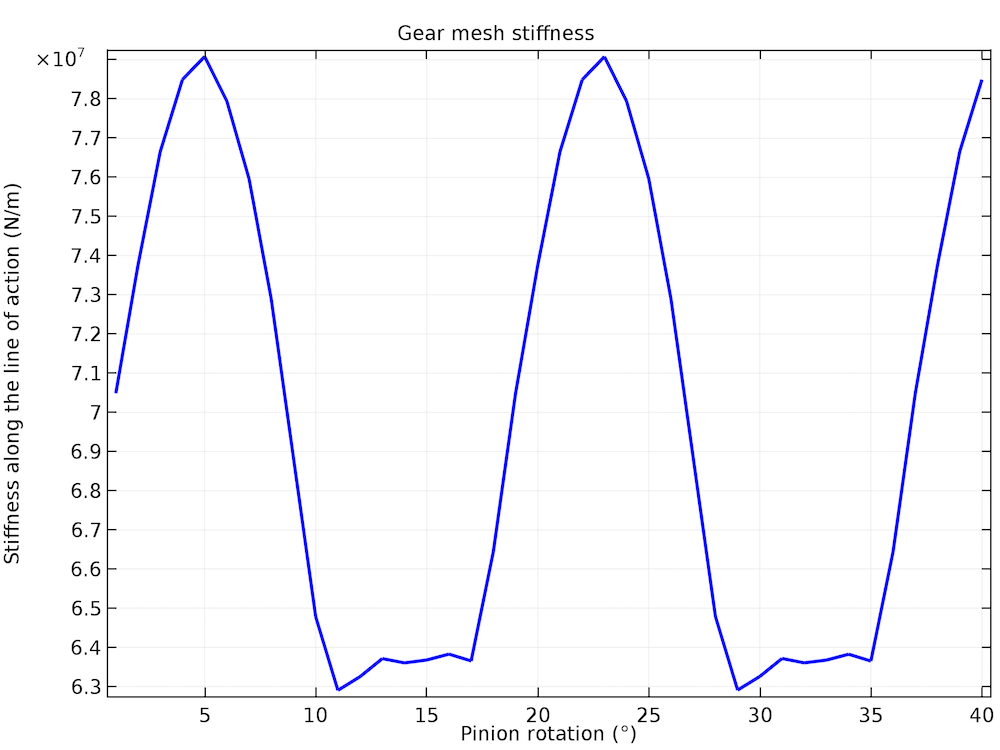
齿轮啮合刚度随小齿轮旋转而变化。
不同参数对齿轮啮合刚度的影响
在上一节中,我们了解了齿轮啮合刚度随齿轮在啮合循环中的位置而变化。它还取决于其他几个参数,这里我们列出了其中的一些:
- 齿参数
- 齿数或模数
- 压力角(齿面与齿轮切线之间的角度)
- 齿顶高(从节距表面到齿最外点的径向距离)
- 几何参数
- 中径
- 宽度
- 材料性能
下面,我们重点研究齿轮参数对啮合刚度的影响。我们使用与第一张表中相同的几何和材料特性。
情况 1:齿数或模数对啮合刚度的影响
为了观察齿数或模数对齿轮啮合刚度的影响,我们考虑了副齿轮上不同的齿数值。
- 副齿轮上的齿数:np= 20,28,36
然后,将齿轮比设置为 1.5 来计算轮上的齿数。其他两个齿轮上的齿参数固定为以下值:
- 压力角:α= 25°
- 齿顶直径比:adr= 0.6



三个不同齿数值(np= 20、28、36)的齿轮啮合。
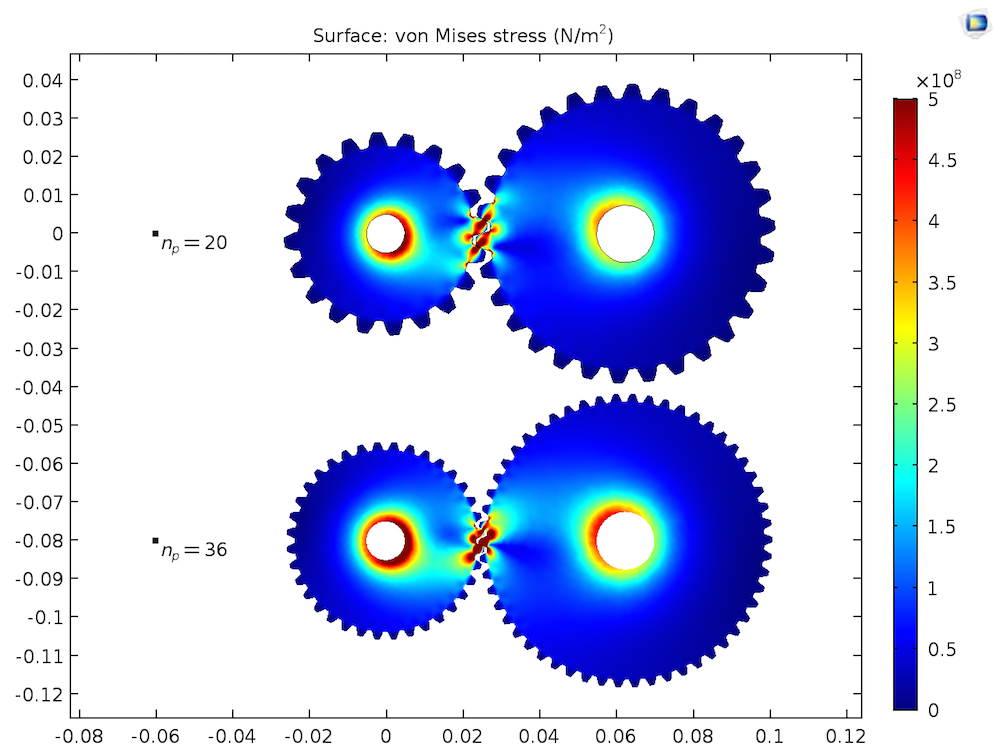
不同 np 值下齿轮副中的 von Mises 应力分布。
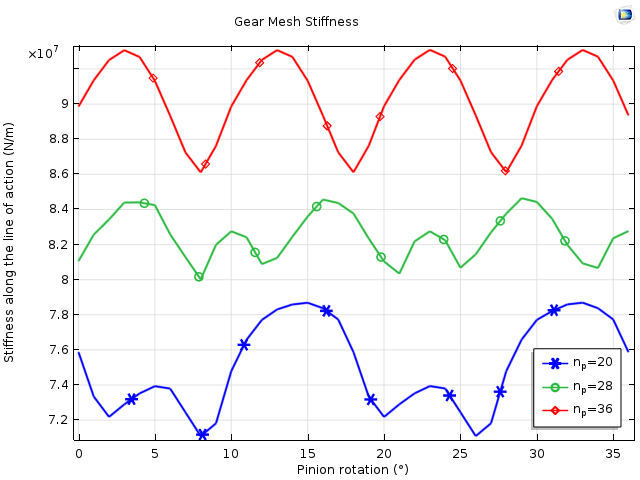
在三个不同齿数值(np= 20、28、36)下,齿轮啮合刚度随副齿轮旋转而变化。对于更多的齿或对于较小的模数,啮合刚度相对较高且较平滑。
情况 2:压力角对啮合刚度的影响
为了解压力角对齿轮啮合刚度的影响,我们来看一下三个不同压力角下的情况。
- 压力角:α=20°,25°,35°
其他两个齿轮齿参数固定为以下值:
- 副齿轮上的齿数:np= 20
- 齿顶直径比:adr= 0.6



三个不同的压力角值(α= 20°,25°,35°)的齿轮啮合。
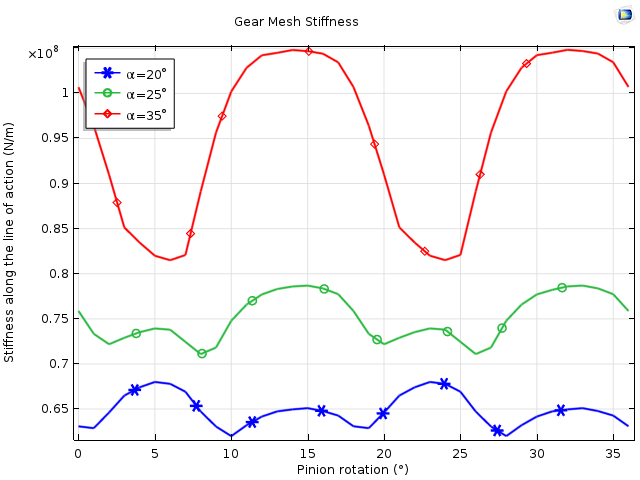
对于三个不同的压力角值(α= 20°,25°,35°),齿轮啮合刚度随副齿轮旋转而变化。啮合刚度随着压力角的增大而增加。
情况 3:齿顶中径比对啮合刚度的影响
在研究了模数和压力角的影响后,我们现在研究不同齿顶值对齿轮啮合刚度的影响。
- 齿顶中径比:adr= 0.6,0.75,0.9
其他两个齿轮齿参数固定为以下值:
- 压力角:α= 25°
- 副齿轮上的齿数:np= 20


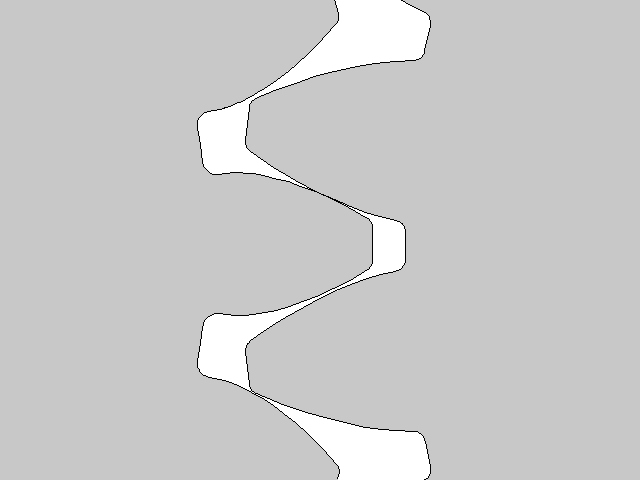
三个不同齿顶中径比的齿轮齿距(adr= 0.6、0.75、0.9)。
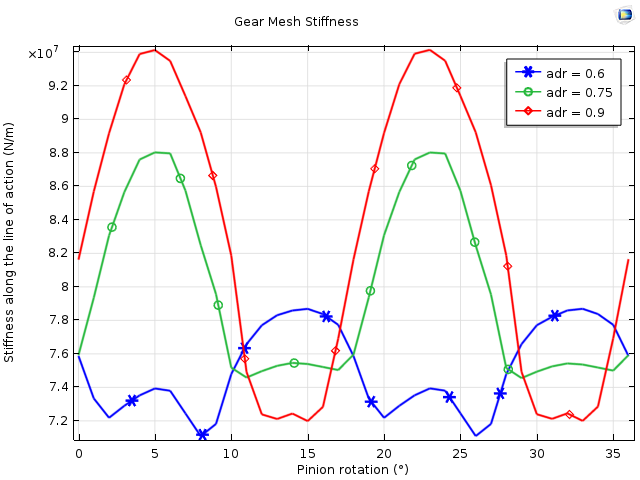
三个不同的齿顶中径比(adr= 0.6、0.75、0.9)下,齿轮啮合刚度随副齿轮旋转的变化。齿顶值越高,刚度相对较高,但是波动也更大。这可能会导致传动系统中的振动水平更高。
在多体动力学分析中考虑齿轮啮合刚度
使用静态接触分析评估齿轮啮合刚度后,下一步是将刚度纳入到齿轮模型中,以便我们可以对整个传动系统进行 NVH 分析。
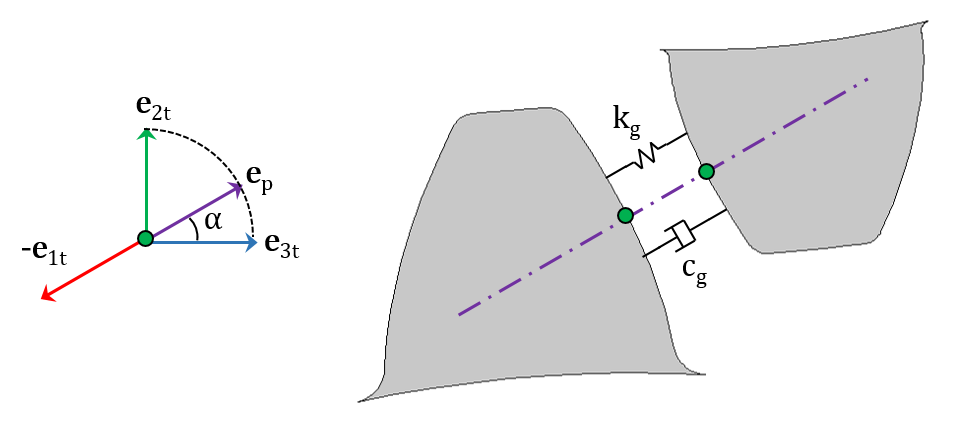
齿轮啮合刚度和阻尼沿两个齿轮之间的作用线增加。
在多体动力学分析中,我们在齿轮副节点下齿轮弹性节点中使用评估的齿轮啮合刚度。在此分析中,我们将齿轮啮合刚度写成齿轮旋转的函数。默认情况下,假定啮合刚度在啮合循环中是周期性的。当然,也可以假设它在一个完整的旋转是周期性的。
为了抑制振动,我们可以在齿轮弹性 节点中添加齿轮啮合阻尼,可以根据啮合刚度的函数输入,也可以显式输入。当齿轮啮合刚度变化可获得时,后一种方法效果很好。如果我们没有确切的齿轮啮合刚度变化,则可以使用齿轮和副齿轮的齿轮刚度。可以通过在齿轮上施加载荷并测量挠度来简单地评估齿的刚度。齿轮刚度也是啮合周期的函数,尽管作为一个近似值,我们可以将其作为一个恒定的平均值输入。
计算齿轮啮合总刚度还需要确定重合度。简单来说,重合度可以定义为在齿轮与配对齿轮接触和脱离接触期间,接触齿数的平均测量值。为了说明不同的重合度如何影响刚度,我们来研究以下几种情况。
情况 1:重合度为 1
在第一种情况下,只有一对齿在啮合循环中的所有位置接触。齿轮齿刚度的典型变化如下所示。
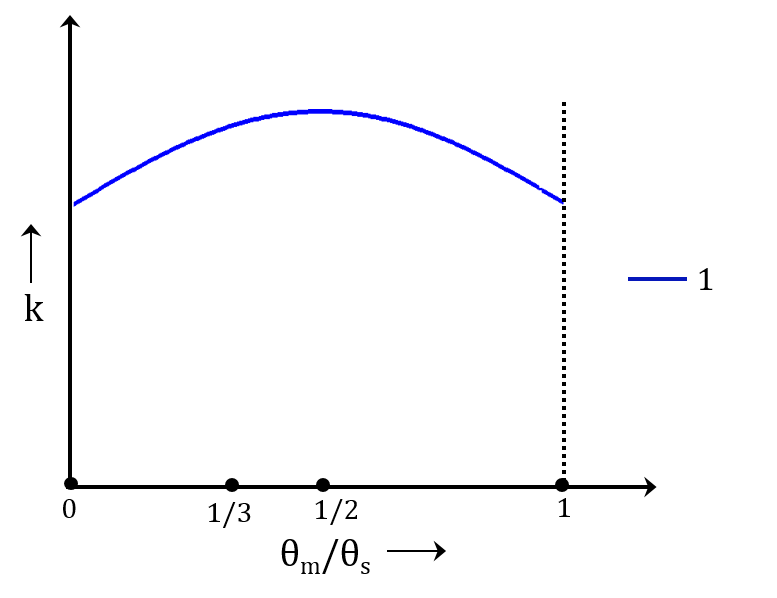
一对接触齿轮的齿刚度的典型变化。
情况 2:重合度为 2
在这种情况下,两对齿在啮合循环中的所有位置都接触。从下图可以看出,除了相位差以外,第二对齿的刚度与第一对齿相同。齿轮啮合的总刚度是单个齿刚度的总和。
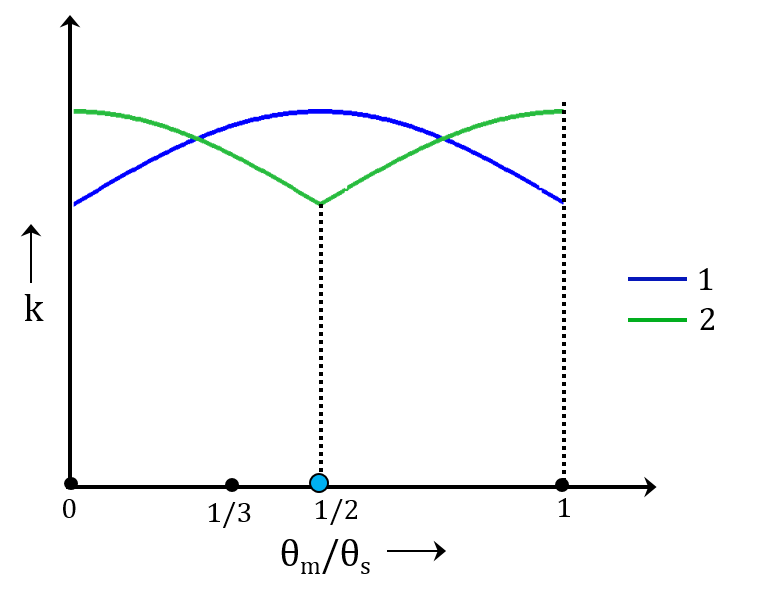
当重合度等于 2时,第一对和第二对齿轮的齿轮齿刚度的典型变化。
情况 3:重合度在 1 和 2 之间
在第三种情况下,接触中的齿对在啮合循环中的不同位置发生变化。对于某些位置,只有一对齿处于接触状态,而在其他位置,则有两对齿处于接触状态。当第二对齿在啮合循环中失去接触时,其刚度变为零。这会导致整体齿轮啮合刚度发生较大波动,从而导致系统振动。
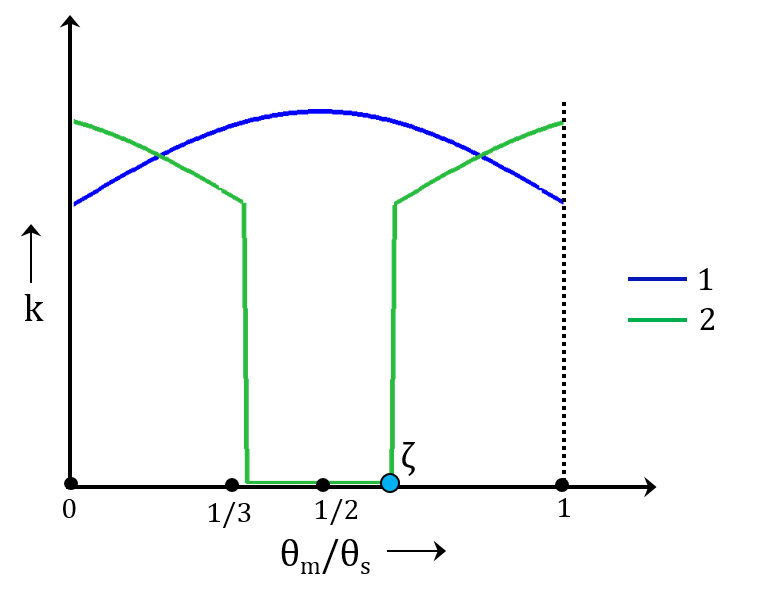
当重合度在 1 和 2 之间时,第一对和第二对齿的齿轮齿刚度的典型变化。
齿轮啮合刚度对斜齿轮动力学的影响
为了证明齿轮啮合刚度对齿轮动力学的影响,我们以一对斜齿轮为例来说明。首先进行瞬态研究,以比较刚性齿轮啮合、恒定刚度的齿轮啮合和变刚度的齿轮啮合。然后,分析不同类型的齿轮啮合对从动齿轮的角速度以及接触力的影响。有关此教程模型的更多详细信息,请参见 COMSOL 案例库。
下图显示了从动齿轮的角速度随驱动齿轮的角速度的变化。对于刚性齿轮啮合,从动齿轮会以恒定的速度旋转。当齿轮啮合刚度恒定时,从动齿轮会先波动,然后再稳定到恒定速度。具有刚度变化的齿轮啮合继续围绕平均值波动,从而引起振动。
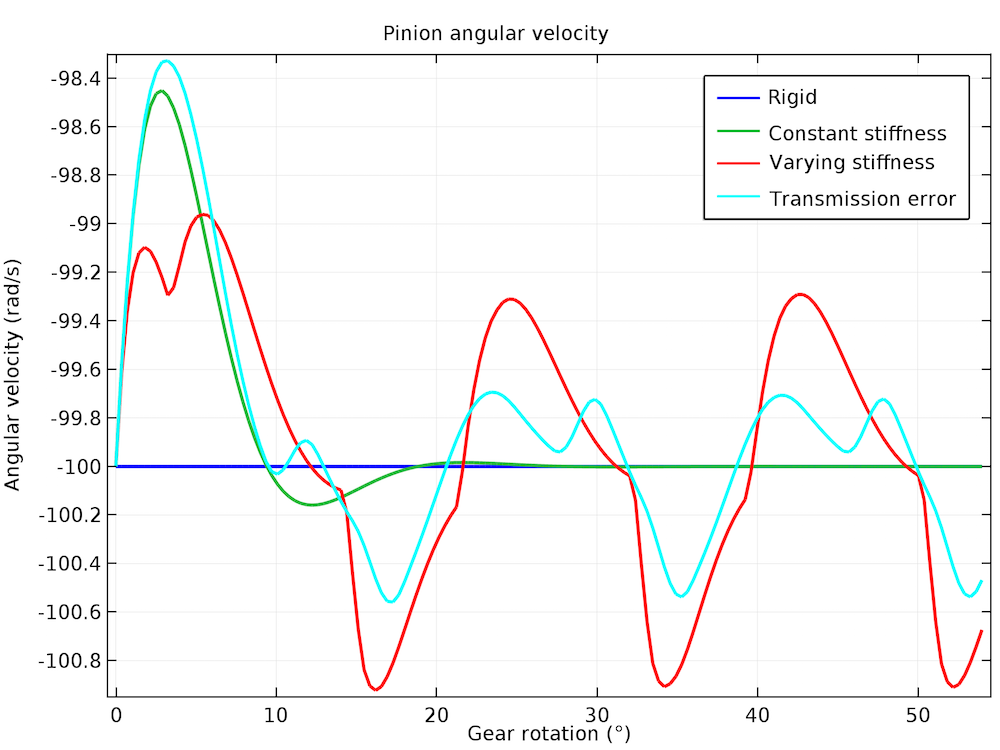
不同类型齿轮啮合的从动齿轮角速度。
我们可以在接触力中观察到类似的趋势。刚性和恒定刚度的齿轮啮合最终保持恒定的接触力,但是变刚度的齿轮啮合会导致接触力在平均值上下波动。接触力的变化相对于啮合周期是周期性的,并且接触力在 150N~450N 之间变化,平均值为250 N。啮合周期中接触力的这种较大变化会引起系统其他部分的振动。这可能会在周围区域产生噪声辐射。
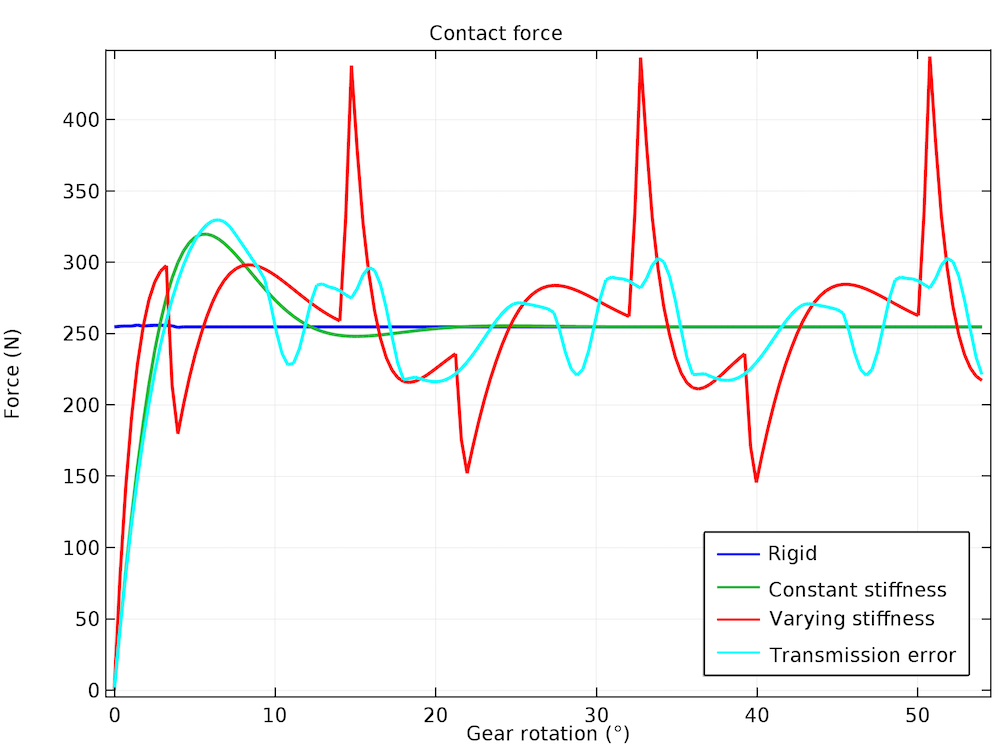
对于不同类型的齿轮啮合,接触力随齿轮旋转而变化。
结语
齿轮啮合刚度的变化取决于多个几何和材料参数,在传动系统的 NVH 分析中起着重要作用。借助 COMSOL Multiphysics 和其附加的多体动力学模块,我们可以通过结合接触分析与零件库中的参数化齿轮来计算齿轮啮合刚度的变化。然后,在多体动力学模型中使用计算出的齿轮啮合刚度来准确地捕获与传动系统其他部分一起工作的齿轮的动力学。
请继续关注齿轮模拟系列博客中的下一篇博客文章,我们将向您展示如何模拟由于齿轮啮合刚度变化而产生的变速箱噪声和振动。同时,建议您浏览下面列出的其他资源。
了解有关齿轮和多体动力学建模的更多信息






评论 (0)