
使用 COMSOL Multiphysics® 软件中结果 节点下的工具,可以生成并可视化具有由谱密度分布决定的、指定统计属性的随机材料数据。这篇博客中,我们将介绍一些常见的例子,它们在许多领域都有潜在的应用,包括热传导、结构力学、地下水流等。
合成随机非均匀材料数据
我们已在博客“如何在 COMSOL Multiphysics® 中生成随机曲面”中讨论过如何通过将 sum 与 if 运算符与均匀分布和高斯随机分布函数相结合来生成外观随机的几何表面。我们的思路是,通过仔细选择振幅和相位角,对一组空间变化的波进行求和,可以模仿自然材料和许多自然现象中经常发现的随机类型。
为了生成二维的合成材料数据,我们可以使用上一篇博客中用来创建随机 CAD 表面数据的双重求和表达式。
请注意,这个求和也可以用来生成随机数据,用于三维模型中表面的边界条件。
对于三维模型,我们需要三重求和:
对于二维和三维模型,与频率相关的振幅将将分别根据下列等式
{g(k,l)}{\vert k^2+l^2\vert^{\beta}}=\frac{g(k,l)}
{(k^2+l^2)^{\frac
{\beta}{2}}}
和
从一个随机分布中取值。
函数 g(k,l) 和 g(k,l,m) 具有随机高斯或正态分布,h(k,l) 和 h(k,l,m) 是与频率有关的振幅函数,其值根据频谱指数 β 在较高频率下逐渐变小,频谱指数的值越高,生成的数据就越平滑。由于各种原因,许多自然过程具有这种特性,其特点是较慢的变化比快速的变化更多。
相位角 φ 从函数 u 中取样,该函数在 -\frac{\pi}{2} 和 \frac{\pi}{2} 之间具有均匀的随机分布:φ(k,l) = u(k,l) 和 φ(k,l,m) = u(k,l,m)
在一组离散的频率上进行求和。求和中更多的非零项意味着有更多的高频贡献,从而使数据包含更多的细节。每个方向上的最大频率分别由整数 K、L 和 M 决定。这些类型的求和与离散反余弦变换密切相关。它们基本上对应于振幅系数 g(k,l)和g(k,l,m) 的反余弦变换,并对相位角做了一些额外的处理。详见之前的博客文章:如何在 COMSOL Multiphysics 中生成随机曲面。
双重和三重求和的表达式
在 COMSOL Multiphysics 中,可以在各种编辑字段中输入以下双重求和表达式,例如二维材料属性或三维边界条件。
0.01*sum(sum(if((k!=0)||(l!=0),((k^2+l^2)^(-b/2))*g1(k,l)*cos(2*pi*(k*s1+l*s2)+u1(k,l)),0),k,-N,N) ,l,-N,N)
也可以用类似的表达方式来表达三重求和,用于三维材料数据、载荷、源和汇:
0.01*sum(sum(sum(if((k!=0)||(l!=0)||(m!=0),((k^2+l^2+m^2)^(-b/2))*g1(k,l,m)*cos(2*pi*(k*x+l*y+m*z)+u1(k,l,m)),0),k,-N,N),l,-N,N),m,-N,N)
这里,我们设定 K=L=M=N。
关于这里使用的基础理论和语法的更多细节,请参见上面提到的博客文章。
处理包含三重求和的模型的计算代价相当高。更有效的做法是比如在一个单独的模型中,首先生成数据并将其导出到文件,然后作为插值函数再次导入。然后,这个插值函数可以以各种方式使用,我们将在后面对此进行解释。另外,还可以使用外部软件通过反 FFT 的方式来生成数据。
现在,让我们来看看如何生成三维材料数据。
在 COMSOL Multiphysics® 中生成一个随机插值表
创建一个随机数据的三维体积矩阵出乎意料的简单。它相当于创建几个随机函数、一些参数、一个网格数据集和一个导出节点。
首先,为振幅创建一个具有 3 个输入参数的随机函数,该函数基于正态分布或高斯分布。这对应于上述数学描述中的函数 g(k,l,m)。在这个案例中,我们任意使用随机函数的默认设置,将平均值设为 0,标准差设为 1。
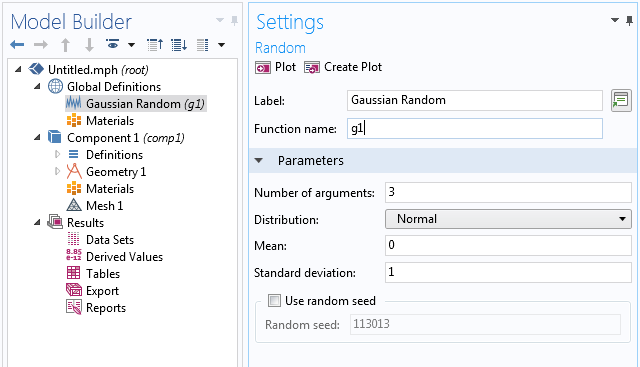
接下来,我们根据上述在 -\frac{\pi} {2} 和 \frac{\pi}{2}
之间均匀分布的函数 u(k,l,m),为相位角创建一个具有 3 个输入参数的随机函数,并与之对应。
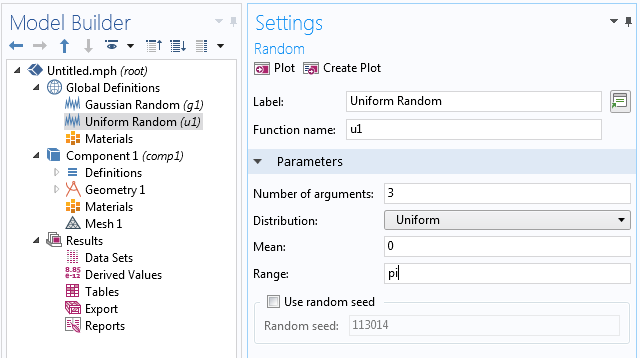
现在,创建一个三维栅格 类型的数据集,引用随机函数作为源。我们需要这个数据集给三重求和表达式提供一个评估环境,这个表达式我们稍后将在导出 节点中定义。
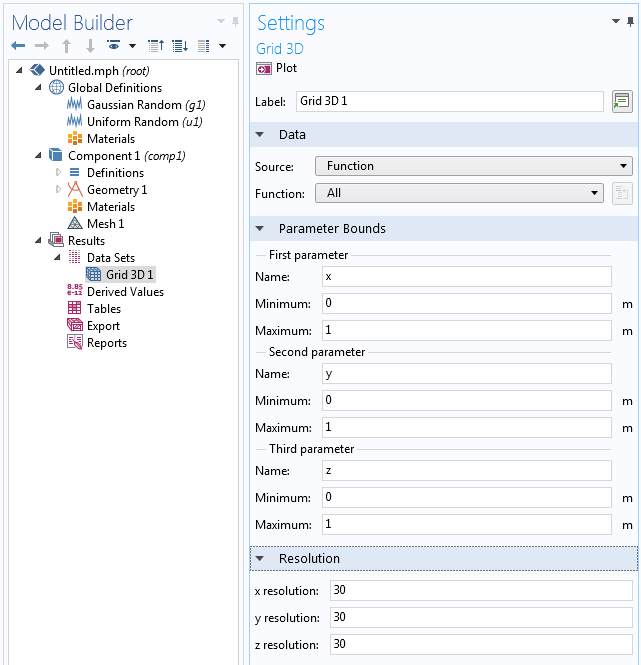
我们将使用两个结果参数,N 和 b,分别用于空间频率分辨率和光谱指数。
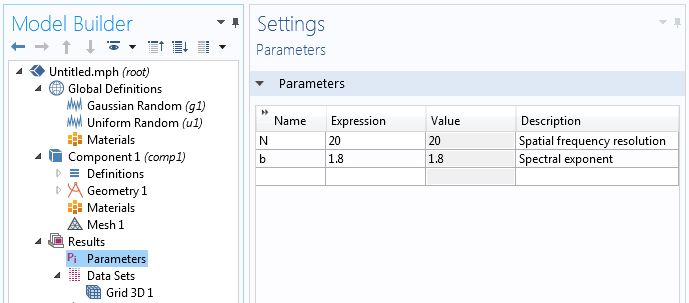
为了更容易处理生成的大数据集,可以关闭自动更新图的选项。这个设置在结果 节点的设置窗口中可用。关闭它可以避免在每次点击结果 下的绘图组时重新计算表达式。
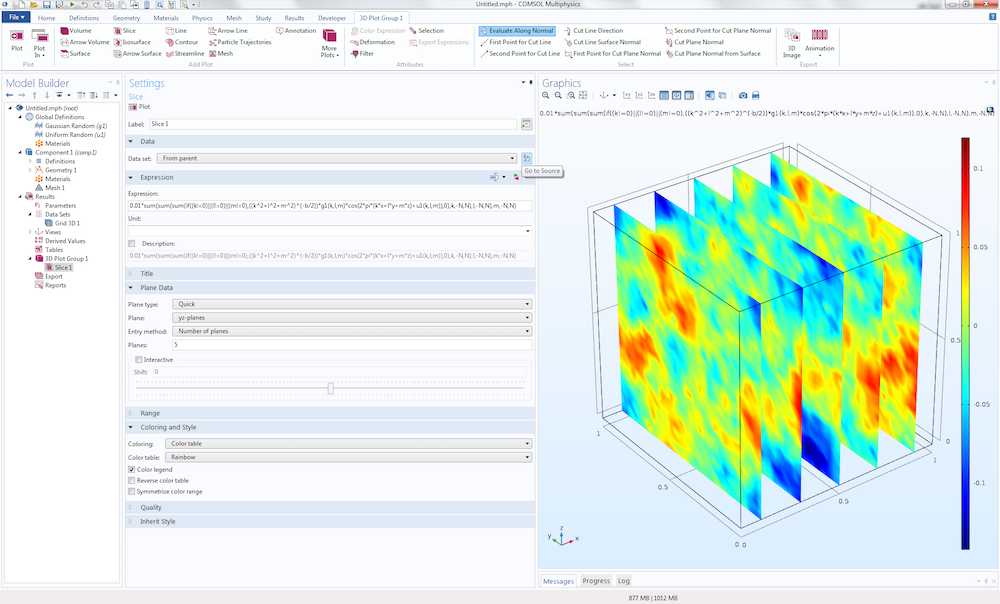
要在导出文件之前实现数据的可视化,可以添加一个切面图并输入(或粘贴)表达式:
0.01*sum(sum(sum(if((k!=0)||(l!=0)||(m!=0),((k^2+l^2+m^2)^(-b/2))*g1(k,l,m)*cos(2*pi*(k*x+l*y+m*z)+u1(k,l,m)),0),k,-N,N),l,-N,N),m,-N,N)
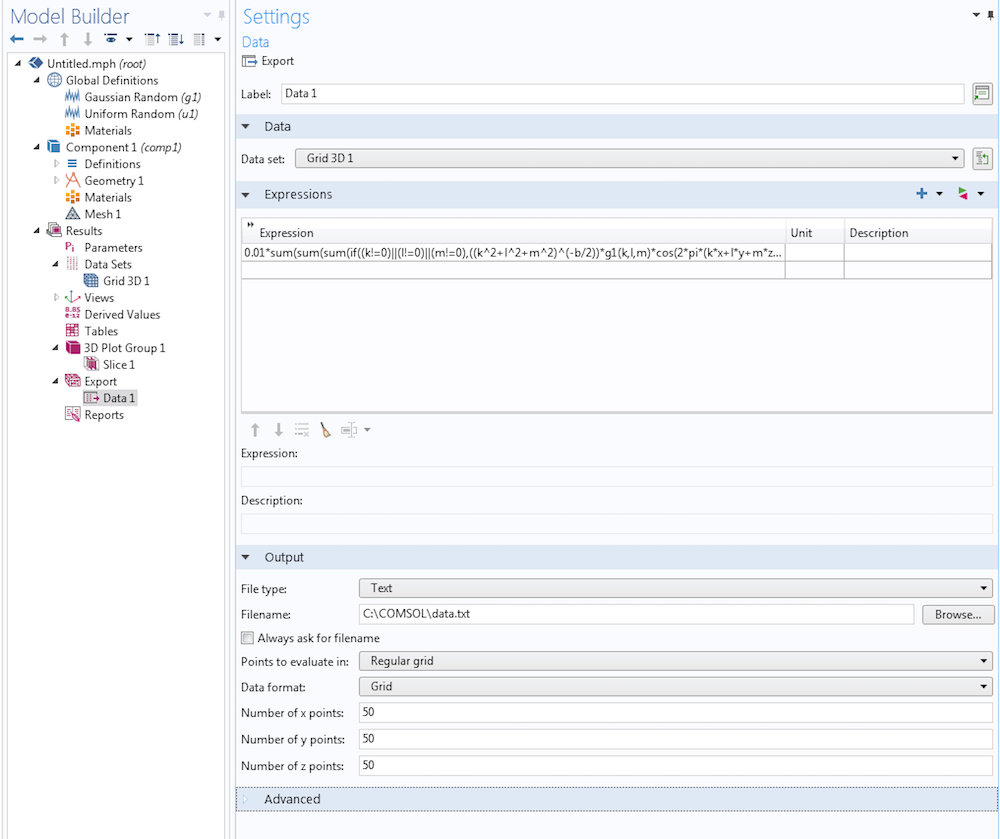
为了导出数据,在导出 下添加一个数据 节点,并键入与上述切面 图相同的表达式。在 数据 节点的设置窗口中,确保将数据集设置为三维格栅,并指定数据将被写入的文件名。在这里,我们可以让这些点以独立于网格三维数据集的方式进行评估。
对于要计算的点 节点的设置,选择规则格栅。对于数据格式,选择格栅。可以自由选择要计算的 x、y、z 点的数量。在下图中,这些点都被设置为 50。注意,对应于高于 50 的数据生成可能需要很长的时间。对于一个 50x50x50 的网格,我们已经得到了 125,000 个数据点。
生成并导出的文本文件现在可以导入到一个新的文件中,目的是设置物理场分析,并在材料属性中使用生成的数据。这可以用于任何类型的物理场,包括电磁学、结构力学、声学、CFD、传热学和化学分析。例如,通过在方法或应用程序中使用 COMSOL® API,这种导出和导入操作可以自动化,并在 for-loop 背景下设置,以便在更大的样本集上生成统计数据。在这个例子中,我们只生成了一组数据。
在传热分析中使用生成的数据
为了说明如何使用这种类型的数据,我们基于传热分析创建了一个最简单的测试模型。
首先,使用固体传热 接口创建一个新的三维模型。
然后,从文件中导入数据作为插值函数。这个函数将在全局定义 节点下可用。
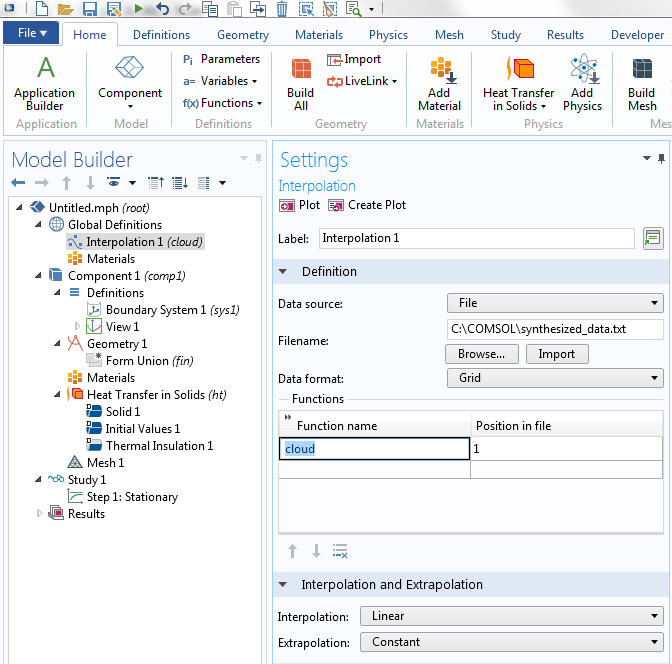
插值函数被命名为 cloud,以后可以用 cloud(x,y,z) 这样的表达式来访问。
为了便于单位处理,在使用这个插值函数时,我们将输入参数变元单位设置为 m,函数单位 设置为 1。 该函数单位对应于 f(x,y,z)=cloud(x,y,z) 的单位,设置为 1 使其无量纲。
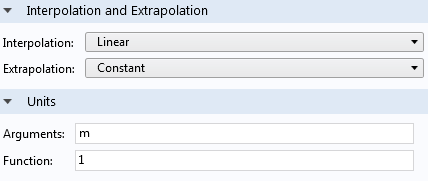
为了简单起见,让我们使用一个与导入的数据完全匹配的块 几何对象,其角在原点,边在 1,与之前用于生成数据的三维格栅 数据集的大小和位置相对应。
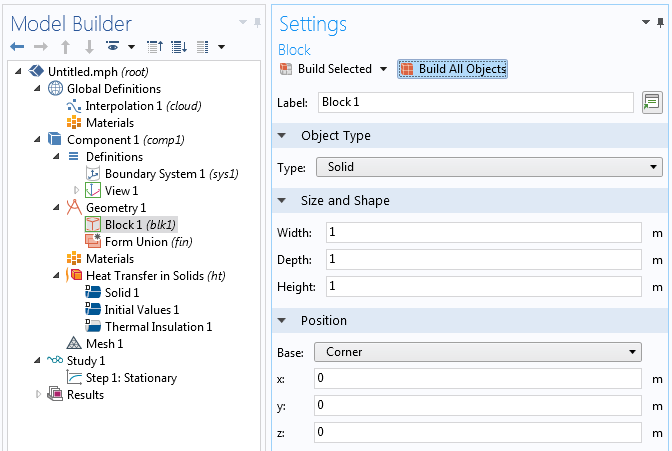
对于一个“真实的”案例,也可以导入或创建一个 CAD 几何体,它可以被用来以适当的方式截断插值函数。这种数据的截断在COMSOL Multiphysics 中是自动的。下图显示了在一个扳手的 CAD 模型上的随机数据的这种内插。当在一个任意的几何体上进行评估时,在三倍求和中对坐标值进行缩放可能是有用的。在扳手的例子中,不是像上面的表达式那样使用 k*x+l*y+m*z,而是使用缩放的表达式 k*(x/0.05)+l*(y/0.05)+m*(z/0.05)。
这类不规则材料数据可用于材料的统计建模,例如在增材制造中使用的那些材料,即 3D 打印部件完美的材料均匀性可能并不总是可能实现。这些数据可用于任何类型的材料特性,如传导性、渗透性和弹性,等等。
回到我们的单位立方体示例,现在我们添加一个空材料节点。随意地将密度设置为 2000 kg/m3,恒压热容设置为 1 J/kg/K。由于我们正在进行瞬态分析,热容量是不相关的。导热系数的表达式被设置为 1+2[W/m/K]*cloud(x,y,z)。我们可以从之前的可视化切面图中看到,插值表的数值大致在 -0.2~0.2。这意味着这个表达式将产生一个有趣的热导率值的空间分布,大约在 0.6~1.4。
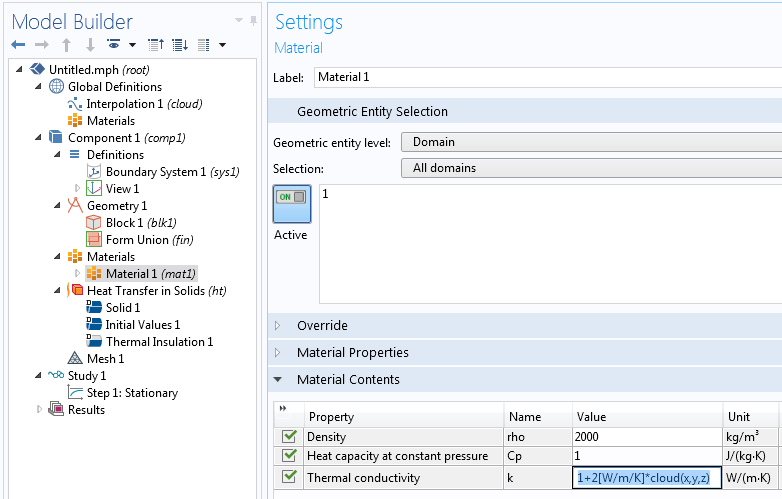
系数 2[W/m/K] 是用来为表达式分配一个一致的单位。常数1将被自动转换为正确的单位:[W/m/K]。
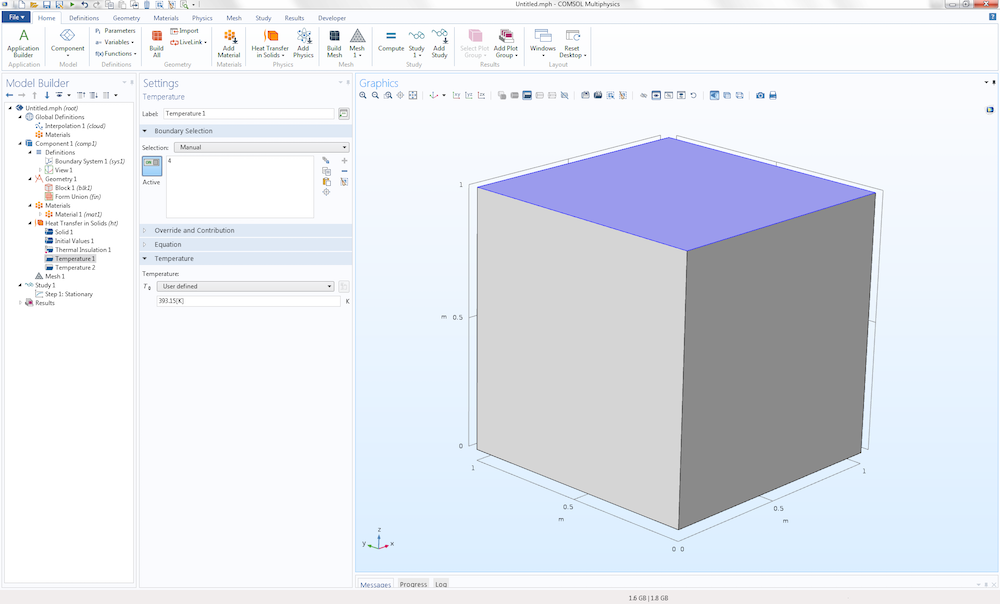
让我们定义一些简单的边界条件。设置顶面的温度为 393.15[K],底面的温度为 293.15[K],对应于 100K 的温差。
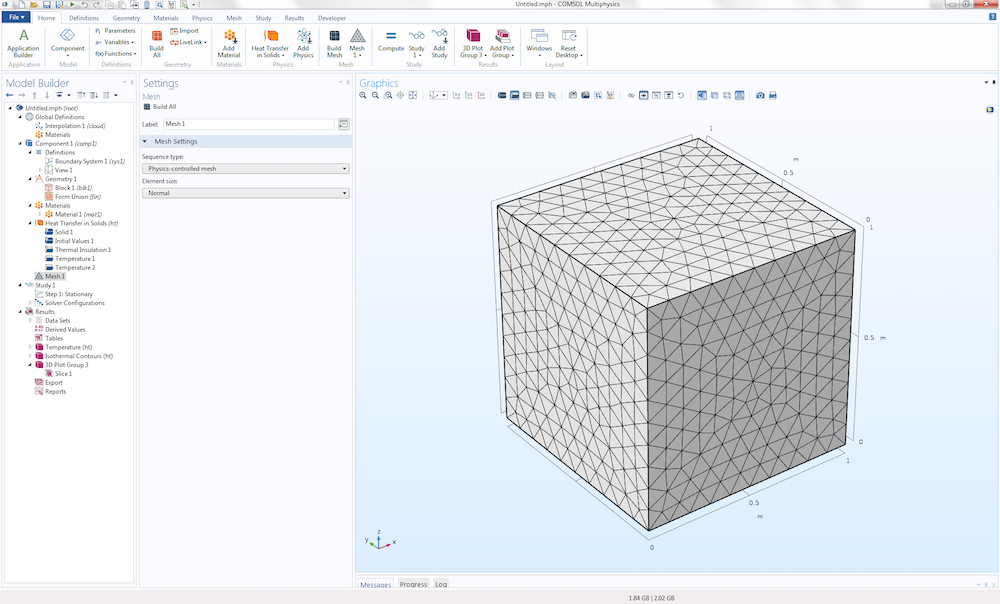
现在,我们来生成一些默认的网格。
COMSOL Multiphysics 将自动从导入的插值函数中向这个非结构化网格插值,比如材料属性的值。另外,我们可以用与原始数据相同大小的六面体单元生成一个扫面网格,即 50x50x50。这样的表示方法会更 “真实”地反映原始数据。
可以尝试使用不同的单元阶数,比如线性和二次元类型。除非使用一个非常细的网格来“过度采样”数据,否则结果将在一定程度上取决于单元顺序。
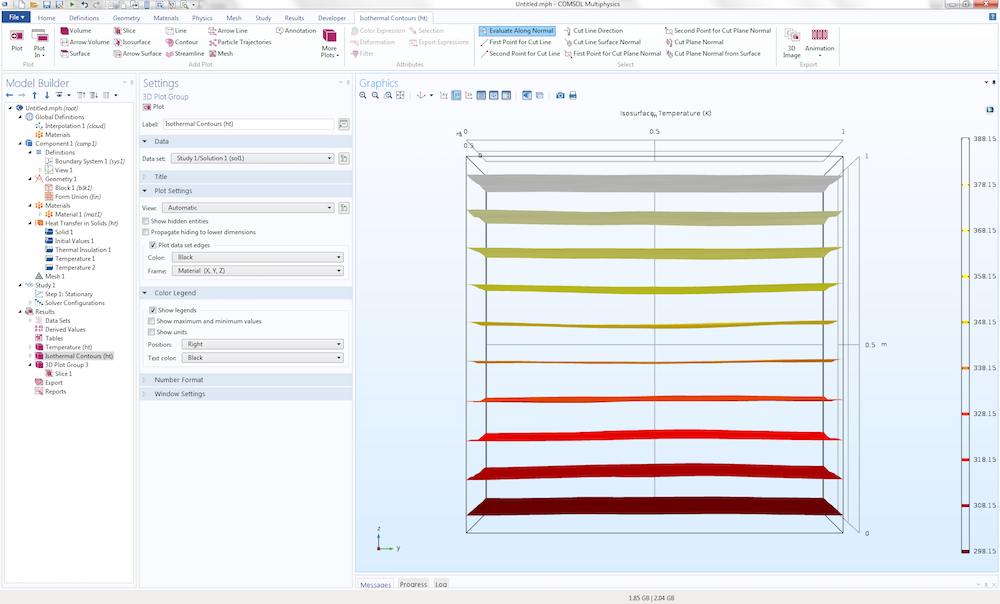
运行研究 将产生2个温度图,其中第二个是等值面 图。
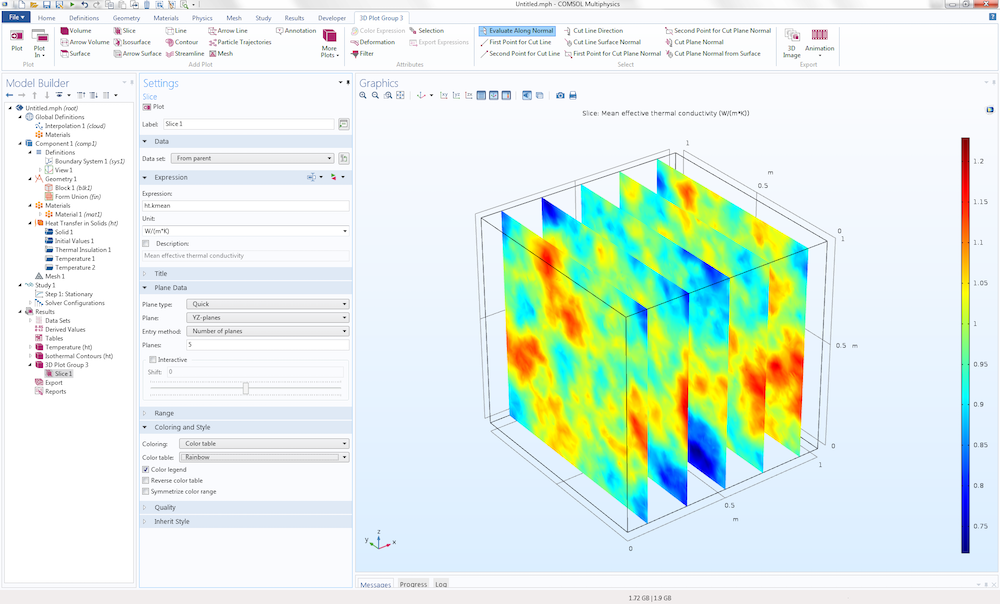
注意到,等值面 图看起来有点像锯齿状,这是由于材料数据的不规则性造成的。我们可以创建另一个切面图,再次将数据可视化。这一次,我们根据热导率,通过使用变量 ht.kmean 来实现,它相当于前面定义的表达式 1+2[W/m/K]*cloud(x,y,z)。
这里,数据的采样密度比原始插值函数低,因为我们使用了默认的网格,单元大小 设置为默认的正常 设置。连续细化这个非结构化的网格,最终将以与原始合成数据差不多的细节水平对数据进行采样。
如前所述,这里用于传热的方法几乎适用于任何其他类型的仿真。例如,在多孔介质流动仿真中,随机的数量是渗透率而不是导热系数。对于多孔介质流,可能需要一个更高级的随机分布,我们将在后面的博客中进行讨论。
二进制数据和渗流效应
我们还可以用另一种方式来使用合成的数据:通过使用布尔表达式将其转换为二进制数据。这种方法可用于模拟两种或多种材料,这些材料界面是随机的,材料特性从一点到另一点会突然发生变化。COMSOL Multiphysics 将自动处理这种情况下需要的尖锐插值。
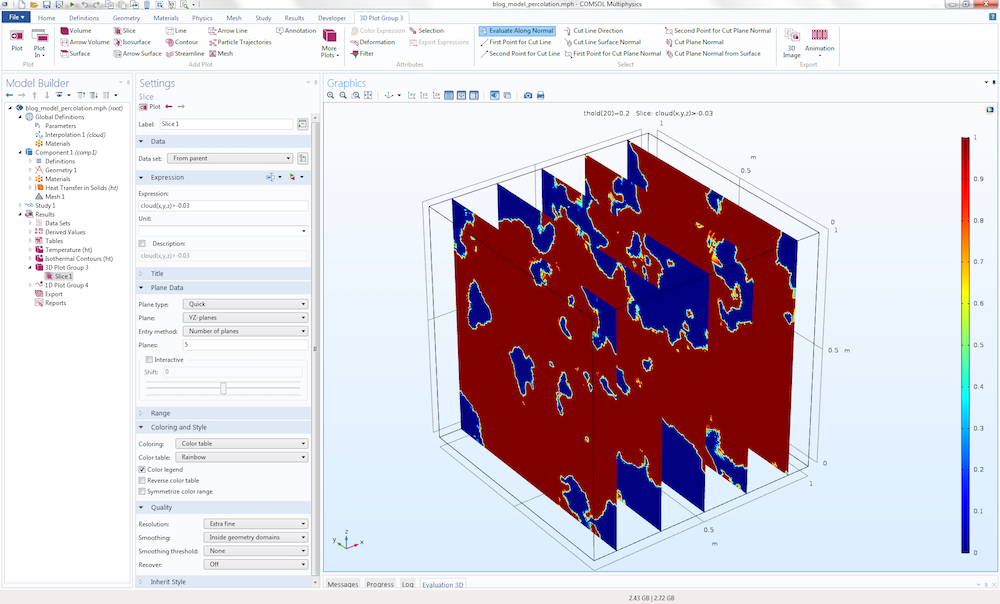
下图显示了布尔表达式 cloud(x,y,z) > -0.03 的可视化图,该表达式在不等式为真的点上计算为 1,在其他点上计算为 0。
为了得到一个更漂亮的图,可以将切面图的分辨率设置为超细化。这个设置可以在切面 图设置窗口的质量 部分找到。
我们现在想在仿真中使用这种类型的二进制信息。例如,在传热仿真中使用它来观察所谓的渗流 效应可能很有趣。对于某些阈值,会在材料中得到一个大的连接分量,这样整个材料板块开始更有效地传导。
要尝试这一点,可以将导热系数的表达式改为 1-0.9[W/m/K]*(cloud(x,y,z)>thold),其中 thold 是一个全局参数。首先在全局定义 下的参数 中定义 thold。
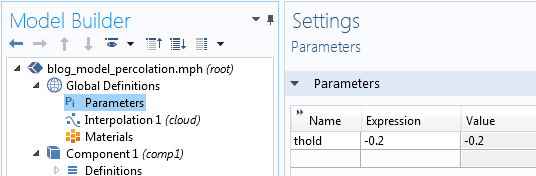
然后,相应地改变材料数据。
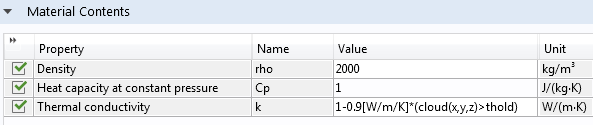
对于空间内每一个点,导热系数 将会以二进制方式计算为 1 或者 0.1。这取决于不等式的值。
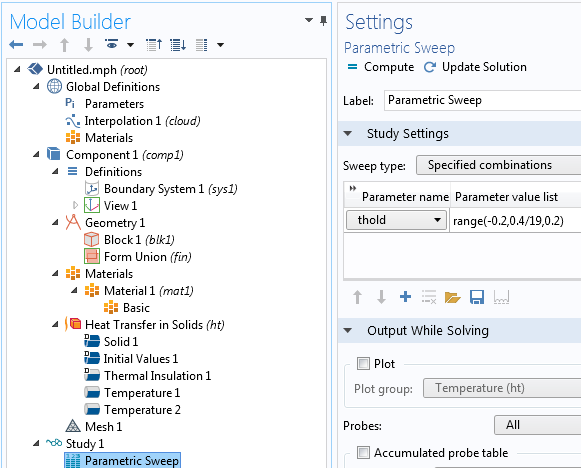
现在,让我们看看这个布尔阈值的不同值将如何影响仿真。为此,在参数 thold 从 -0.2 到 0.2 之间运行参数扫描。
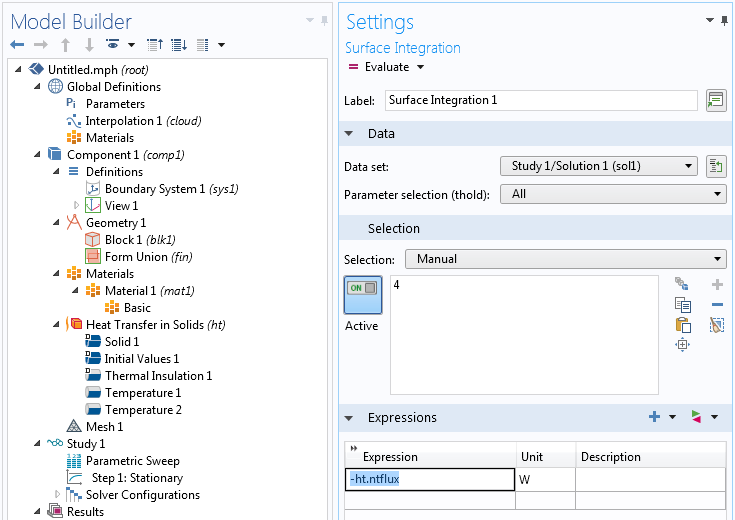
在派生值 下添加一个表面积分节点,对通过其中一个表面的总热通量进行积分。这将由 -ht.ntflux 或 +ht.ntflux 的表面积分给出,取决于是对顶面还是底面进行积分。在下图中,我们使用的是顶面。
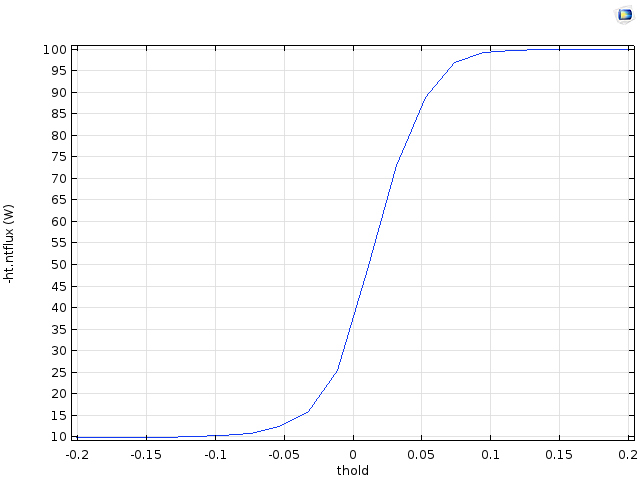
产生的结果表 图显示了热功率转移的量(以瓦特为单位)。可以看到,对于 0 左右的阈值,传导率从低值迅速上升到高值。这是由于突然出现了一个或多个大的连接部件,其表达式 1-0.9[W/m/K]*(cloud(x,y,z)>thold)被计算为1。
下面的数字显示了在 0 左右的三个阈值下带有过滤器 属性的体积图。过滤器显示了 cloud(x,y,z)<thold 的域的部分,对应于较高的电导率位置。
我们可以从这些数字中看到高导电性的部分是如何开始连接较高的阈值的。
相应的过滤器设置如下图所示。
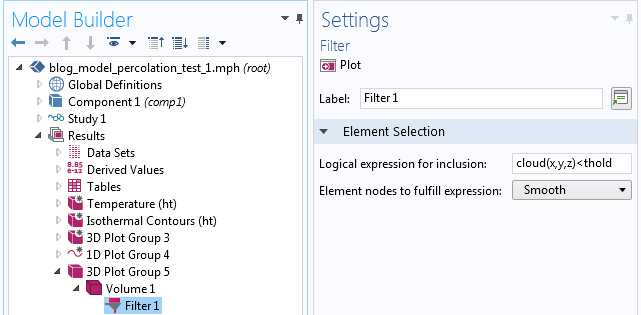
类似的渗滤效应,在这里看到的是二进制数据,在前面显示的连续数据情况下也发生了。然而,当使用二进制数据时,其效果更容易看到。
点阵图的可视化
最后,让我们看看将这种类型的随机数据可视化的另一种方法。我们将使用大量的随机点(或者说,小球体)来可视化数据集,并让这些点的半径和颜色根据插值函数 cloud(x,y,z) 而变化。此外,我们将只允许 cloud(x,y,z) 的正值的点被可视化。这种技术使我们以一种用其他方法难以实现的方式 “看到数据内部”。请注意,这种可视化技术适用于任何类型的数据,包括真实的测量数据。
首先,生成三个均匀分布的随机变量,范围设置为 1,平均值设置为 0.5
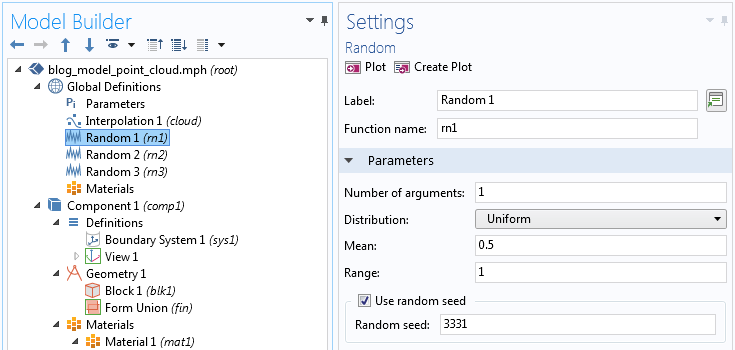
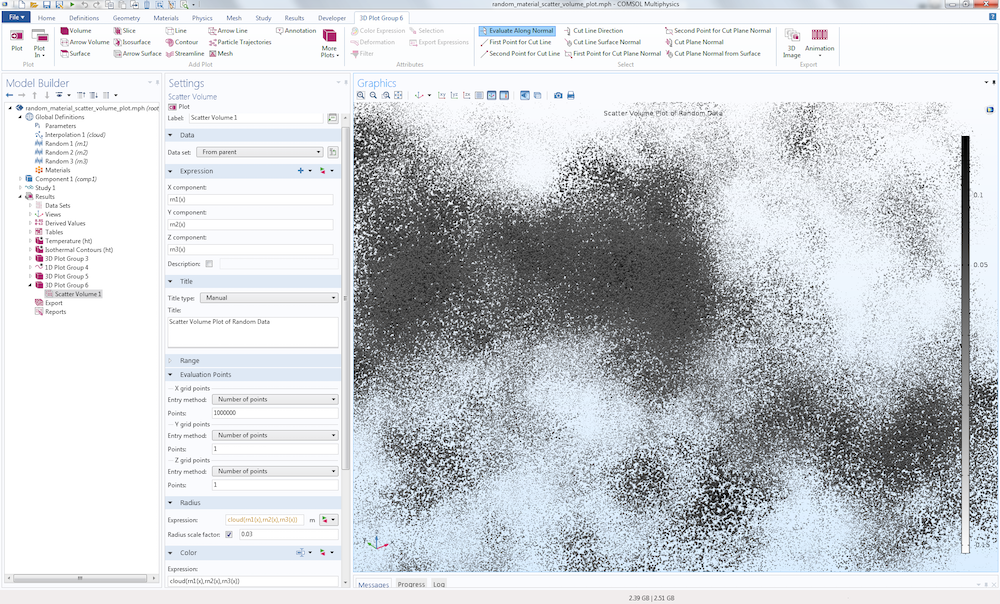
为了生成这种类型的绘图,我们使用散射体图类型。这可以通过右击三维绘图组 并选择更多绘图>散射体 来实现。
在散射体图 的设置窗口中,分别设置 X、Y 和 Z 分量的表达式:rn1(x)、rn2(x) 和 rn3(x)。在这里,我们以一种不寻常的方式使用 x 坐标,因为我们只是把它作为一个任意值的长矢量。
接下来,在计算点 部分,将 X 网格点的点数设置为 100,000;1,000,000 或更多,这取决于你的计算机能处理多少个点。这是一个获得长数值矢量的技巧,我们可以将其输入随机函数,以便在单位立方体中产生大量的随机点。
为了使绘图出现在上图中,进入半径部分,将表达式 设置为 cloud(rn1(x),rn2(x),rn3(x)),半径比例因子 设置为 0.3。此外,在颜色部分,将表达式设置为cloud(rn1(x),rn2(x),rn3(x)),颜色表 设置为 GrayScale。
关于这个图还有一个值得注意的事实:负值将被忽略。这有助于我们的可视化,因为生成的数据中大约有一半是负值,我们可以更容易地看透数据,对变化有一个直观的感觉。这种方法只对矩形块有效。如果要在一个任意的 CAD 几何体上生成这种类型的图,可以使用粒子追踪模块,它允许在任何类型的 CAD 模型内生成随机点。

顺便说一下,在二维模型中,只需使用二重求和表达式创建一个二维表面图,就可以实现一个看起来类似的图,如上图所示。









评论 (0)