在结构力学仿真中，可能存在这样一种情况，即你想实现自己的材料模型。你可以使用COMSOL Multiphysics® 软件，选择用 C 代码编写自己的材料模型。然后使用外部材料 特征从程序中调用编译后的代码。在这篇博客中，我们演示了如何实现外部材料模型，并通过一个示例分析如何使用这个功能。
外部材料特征
COMSOL Multiphysics® 的附加产品——非线性结构材料模块内置了大量的材料模型，包括超弹性、各向同性/运动硬化塑性、黏弹性、蠕变、多孔塑性、土壤等模型。这些材料模型涵盖了结构分析中的绝大多数工程问题。
然而，在某些情况下，使用已有的材料模型表示材料的机械行为并不容易。例如，假设你为某种合金开发了一个专门的材料模型，并希望用它来解决 COMSOL Multiphysics 中的一个大型结构力学边值问题。你会怎么做？
你可以通过三种不同的方式定义自己的材料：
- 许多材料模型都有用户定义 选项。例如，你可以通过在 GUI 中直接输入应变能量密度与应变函数的表达式来创建自己的超弹性材料。
- 下一个级别，当没有合适的材料模型可以通过用户定义 选项调整时，可以将材料模型表示为一组单独的 PDE 或 ODE，并使用其中一个数学接口输入适当的表达式。
- 最后，你可以使用外部材料特征 用 C 代码编写自己的材料模型。如果材料模型表示为一种算法，而不是一组方程，这是首选方法。
将材料模型实现为外部 DLL 似乎是一项复杂的工作，这篇博客演示了如何在 COMSOL Multiphysics 中使用规范的操作步骤实现弹塑性材料模型。
在 COMSOL Multiphysics® 中实现弹塑性材料模型
首先，我们需要确定一个要实现的材料模型。选择一种各向同性的线弹性材料，它具有各向同性的硬化。这是 COMSOL Multiphysics 中内置的一个简单塑性模型，可以很好地传达一些关键点。
首先，让我们复习一些假设、定义和命名法：
- 应变是相加的，假设很小
- 弹性响应是线性和各向同性的，由杨氏模量 E 和泊松比 ν 定义（或等效地由体积和剪切模量 K 和 G 定义）
- 塑性响应是各向同性的，初始屈服应力为 \sigma_{ys0}
- 材料的屈服应力是有效塑性应变的函数，\sigma_{ys}=\sigma_{ys0}
+\sigma_h\left(\epsilon_{pe}\right)，具有初始值 \sigma_{h}\left(0\right)=0 (硬化函数) - 塑性流动遵循 J_2 理论
- 有效塑性应变的增量由下式给出 \Delta\epsilon_{pe}=\left(\frac{2}{3}\Delta\bm\epsilon_p:\Delta\bm\epsilon_p\right)^{1/2}
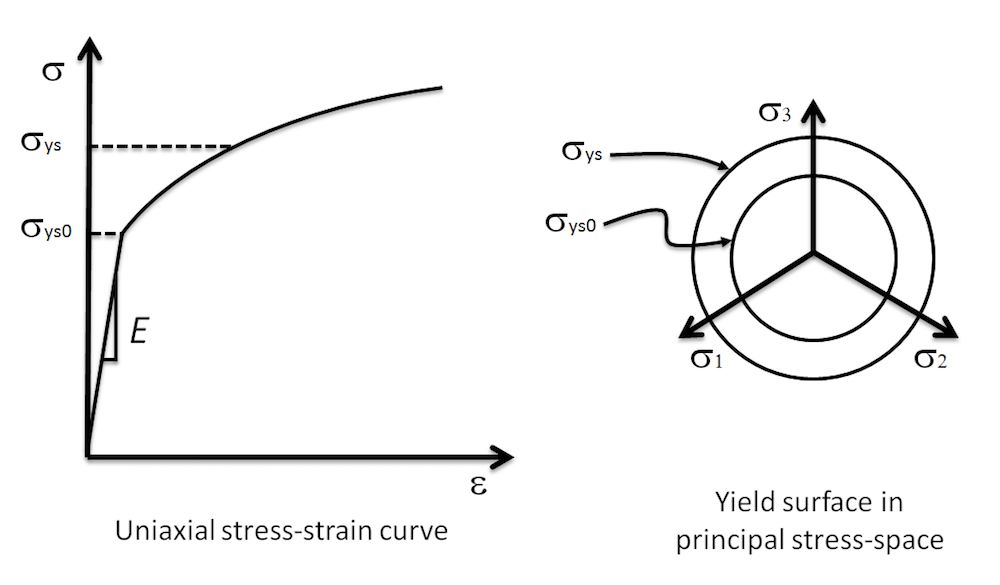
示例材料模型：主应力空间中的单轴应力-应变曲线和屈服面。
现在，我们来讨论将该材料模型作为外部材料来实现的方法。有几种不同的方法来调用用户编码的外部材料例程，我们将其称为套接字。
方法 1：广义应力-应变关系
我们可以使用外部材料的广义应力-应变关系 套接字来定义一个完整的材料模型，包括（可能）弹性和非弹性应变贡献。这是本文讨论的两种建模方法中最通用的一种。当使用广义应力-应变关系 套接字时，我们面临两个任务：
- 应力 张量 \bm{\sigma} 的计算
- 应力 \bm{\sigma} 相对于应变 \bm{\epsilon} 的雅可比行列式的计算
方法 2：非弹性残余应变
我们还可以使用非弹性残余应变 套接字来定义对整体材料模型的非弹性应变贡献 \bm\epsilon_{inel} 的描述。例如，如果我们想将自己的蠕变应变项添加到内置的线弹性材料中。非弹性残余应变 套接字假设了总(格林拉格朗日)应变的加法分解为弹性和非弹性部分。因此，当应变小于 10% 时，这是一个充分的假设。使用外部材料模型的非弹性残余应变 套接字时，我们面临两个任务：
- 非弹性应变 张量的计算 \bm {\epsilon}_{inel}
- 非弹性应变 \bm {\epsilon}_{inel} 相对于应变的 \bm {\epsilon} 雅可比行列式的计算
两个相关的外部材料 套接字分别是广义应力-变形关系 和非弹性残余变形。它们是上述讨论的更通用的版本。不是根据格林拉格朗日应变张量定义变形，而是提供变形梯度。许多大应变弹塑性材料模型使用将变形梯度乘法分解为弹性和塑性部分。在这些情况下，您可能希望使用其中的一个套接字来代替。
提示：在这篇文章的末尾，我们提供了源文件和模型文件的下载链接。
应力张量的计算：应力更新算法
计算应力张量的复杂性因材料模型而异。在实践中，应力张量的计算往往需要用算法来表述。这在文献中通常被称为应力更新算法。本质上，材料模型应力更新算法的目标是计算应力，已知：
- 对应于当前位移场估计的总应变
- 之前收敛增量的材料状态
这些量作为输入提供给外部材料。
术语“材料状态”表示描述材料所需任何依赖解的内部变量。这类变量有塑性应变张量分量、当前屈服应力、背应力张量分量、损伤参数和有效塑性应变等。这类状态变量 的选择取决于材料模型。我们必须确保材料状态在分析开始时被正确初始化，并在增量结束时更新。
首先需要调查在增量过程中是否发生塑性流动。我们通过假设弹性应变等于当前增量 的总应变，减去先前收敛增量 ^{old}\bm\epsilon_{p} 的(偏)塑性应变来做到这一点。如果在增量过程中确实没有塑性流动，这个假设就会成立。以这种方式计算的偏应力张量被称为试验应力偏量，由下式给出
具有有效(von Mises)值 \sigma_{trial,e}。
通过假设在增量过程中没有塑性流动，将有效试验应力与材料的屈服应力进行比较。与先前收敛增量对应的屈服应力由下式给出
如上所述，步骤 1 和 步骤 2 中的左上标 ^{old}\bm\epsilon_p 和 ^{old}\epsilon_{pe}，分别代表先前收敛增量的物质状态。
现在，我们检查试验应力是否会导致塑性流动。另一种表达方式是，如果试验应力在屈服面内，那么在增量过程中响应将是纯弹性的。否则，将导致塑性流动。使用屈服条件进行检查：
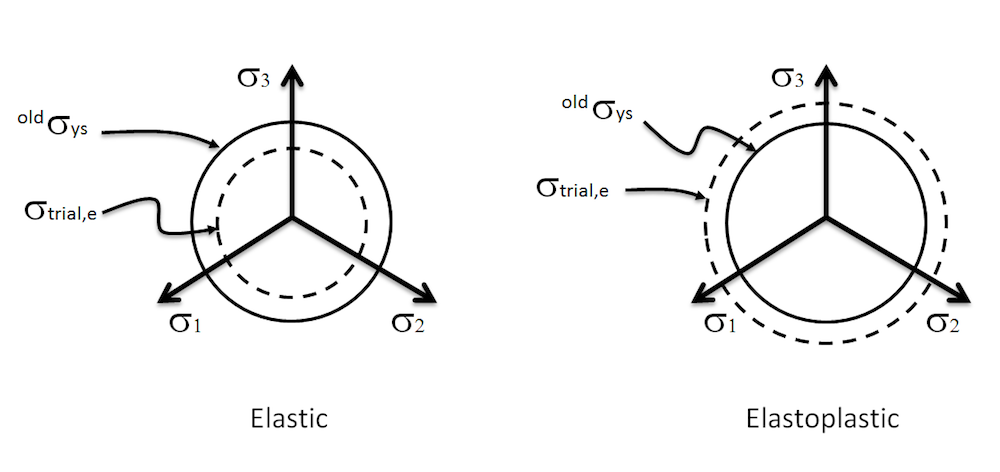
检查屈服条件来确定弹性或弹塑性计算。
现在，应力更新算法必然分为纯弹性计算或弹塑性计算分支。我们将从纯弹性分支开始，分别关注这些分支。
弹性计算
因为我们确定在增量过程中没有塑性流动，所以试验应力偏差实际上与应力偏差相同，塑性应变张量和有效塑性应变的更新是微不足道的。
我们可以直接将纯弹性应力-应变关系写为雅可比行列式。
弹塑性计算
应力更新算法的弹塑性分支的目标是计算应力偏差并 更新塑性应变。我们从再次表达应力偏差开始，已知塑性流动发生在增量期间：
或者
在上面的等式中，我们使用了离散形式的流动法则，它表明塑性应变的增量通过所谓的塑性乘数 \Delta\lambda 与应力偏差成正比。考虑这个应力方程的图形表示：
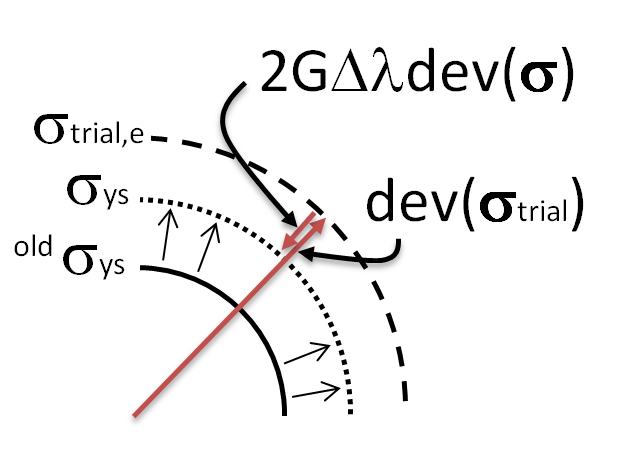
试验应力偏差校正的图形表示。
如果我们计算出的试验应力偏差位于屈服面之外，则需要进行修正，使应力偏差返回到待确定的屈服面。塑性乘数决定了试验应力偏差应按比例缩小的确切量，以得到正确的应力偏差。如果我们计算塑性乘数，就可以直接计算应力偏差和塑性应变增量。
关键步骤是：
- 将应力方程转换为控制标量方程
- 在单个参数中表达所有未知数
- 求解该参数的标量方程
我们可以将塑性乘数与有效塑性应变增量 \Delta\epsilon_{pe} 联系起来，使用流动法则，然后将应力方程转换为控制标量方程：
这通常是一个非线性方程，需要使用合适的迭代方案来求解它。现在我们已经可以计算应力张量、塑性应变张量和有效塑性应变了。
更新的塑性应变张量和有效塑性应变存被储为状态变量。
计算材料的雅可比行列式
我们计算了应力并更新了材料模型的材料状态(状态变量)。现在，我们介绍转向雅可比计算。Jacobian 在文献中还有其他名称，例如切线刚度、切线模量 或切线算子。在应力更新算法中，将应力张量的偏量和静水力部分表示为：
我们要计算的雅可比是第二类皮奥拉-基尔霍夫应力张量相对于格林-拉格朗日应变张量的导数。对于示例中的材料，假设应变很小。这意味着不需要区分应力和应变的各种测量值，因为它们在小应变极限下是无法区分的。关于应变的应力导数 \mathcal{C} 写为
如果使用偏应力和静水压力方程以及试验应力的定义，可以用以下方式表达雅可比行列式：
请注意，在上面的表达式中用总塑性应变张量替换了塑性应变张量的增量。由于塑性应变的附加更新，它们关于应变的导数是相同的。回想一下，我们的两种建模方法需要不同定义的雅可比行列式。我们立刻就能看到它们之间的关系。在 广义应力–应变 关系中，雅可比由上面的完整表达式给出。在非弹性残余应变 中，雅可比由表达式中的一个项给出，即：
项 \mathcal{C}^e 是弹性雅可比行列式。对于纯弹性计算，广义应力–应变 关系的总雅可比等于该量，这时非弹性残余应变 的雅可比为零。
如果使用流动法则和链式法则进行微分，得到以下表达式：
请注意，这个表达式取决于塑性乘数。这表明，对于目前的材料模型，选择非弹性残余应变 而不是广义应力–应变关系 几乎没有什么好处，因为这两种方法都需要一个完整的应力更新算法来计算塑性乘数。对于其他材料模型，如蠕变模型，好处会更大。使用控制标量方程和流动法则，我们可以计算上述表达式中的最后一个导数。
\Delta\epsilon_{pe}}\right) \, \mathrm{dev}
\left(\sigma\right)
为了确保全局方程求解器的快速收敛并最终减少仿真时间，计算的雅可比行列式应该是准确的。那么，准确 是什么意思？简单来说，这意味着计算的导数必须与用于计算应力的应力更新算法一致。也就是说，应力更新算法中使用的任何假设或简化都应该反映在雅可比行列式的计算中。基于应力更新算法的导数通常称为算法或一致 的。
在某些情况下，雅可比计算可能很麻烦。这时，通常可以使用近似雅可比行列式。要记住，解的准确性由压力更新算法决定。只要雅可比距离不太远，全局方程求解器仍将收敛到正确的解，尽管收敛速度较低。
关于雅可比计算的进一步评论
- 外部材料对应力、应变和雅可比行列式使用简化的矢量和矩阵形式。我们需要相应地表述应力更新算法和雅可比计算。
- 进入外部材料的应变矢量使用张量分量表示剪切力。雅可比行列式的定义是假设剪切的张量分量；因此，它通常是非对称的。
- 平面应力是在外部材料特征之外处理的，所以我们只需要对模型进行一次实现。换句话说，我们实现的模型可以直接用于 3D、2D 轴对称和 2D 平面应力和平面应变分析。
应用示例：材料模型的专业化
在上面的章节中，我们开发了一种应力更新算法，并概述了如何计算雅可比行列式。现在，我们将考虑硬化曲线的一个特殊情况。假设屈服应力是有效塑性应变的线性函数。这通常被称为线性硬化，它由一个恒定的 “塑性模量”定义，E_{iso} 是硬化曲线的恒定斜率。事实证明，线性硬化意味着塑性应变增量可以以闭合形式求解。
在这个示例的源代码文件中，我们已将这种专业化用于线性硬化。
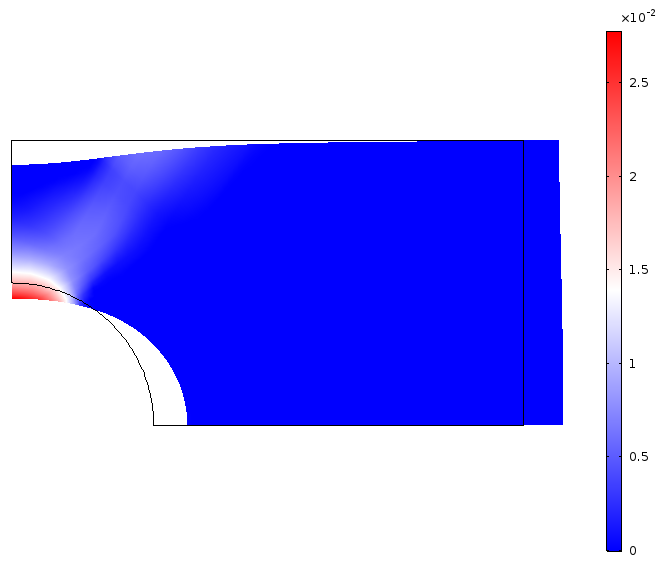
考虑一个用孔拉板的示例问题。
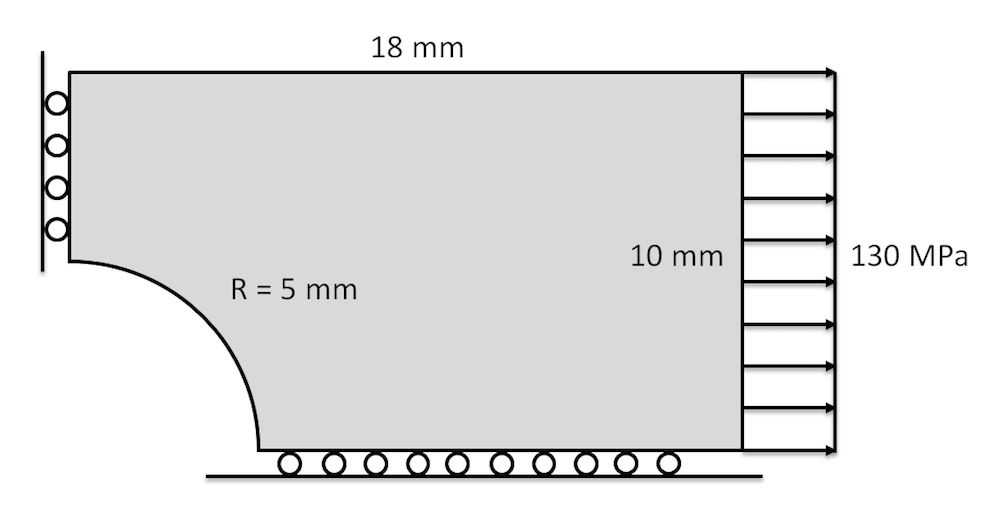
带孔板的尺寸、边界条件和载荷。
这个问题有两个对称平面，并且只模拟了四分之一的板。使用以下材料参数：
- E = 70 GPa
- n = 0.2
- \sigma_{ys0}= 243 MPa
- E_{Tiso} = 2.17 Pa
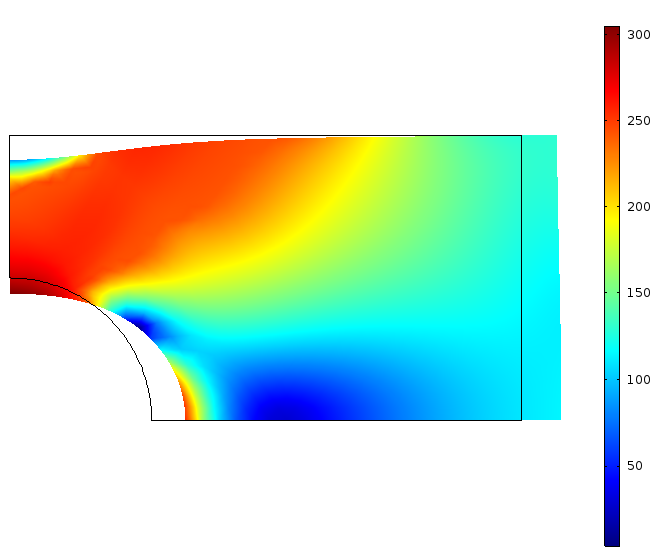
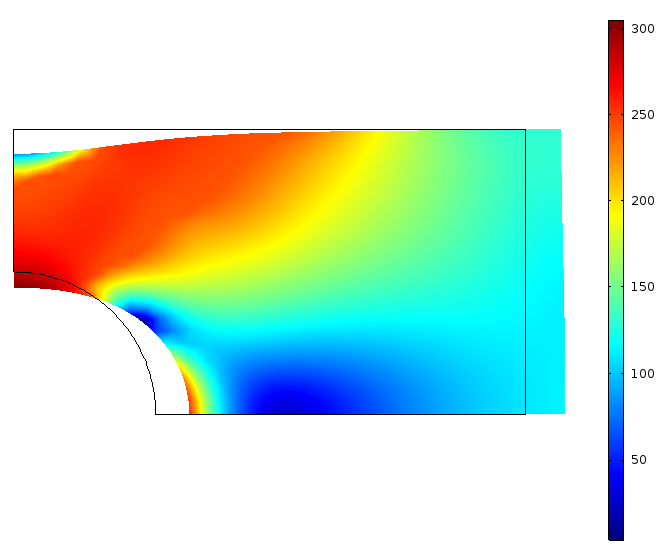
该问题假设为平面应力。我们可以将实现的材料模型的预测与内置模型进行比较。只要求解非线性方程时的容差足够严格，我们预计差异仅在数值四舍五入的数量级内。
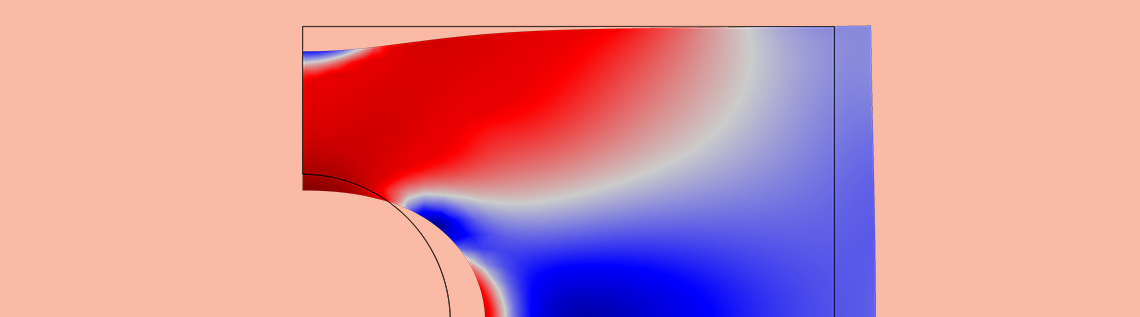
使用外部材料模型(左)和内置材料模型(右)计算的有效 von Mises 应力（以 MPa 为单位）。
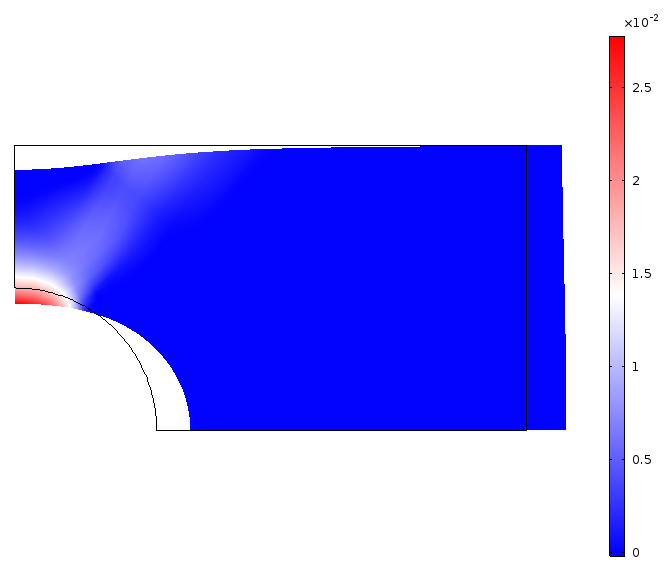
使用外部材料模型(左)和内置材料模型(右)的有效塑性应变计算。
结束语
实际上，我们还可以在更多场景中使用添加外部材料的可能性。
例如有这样一种情况，你有一个已经在另一种情况下得到了验证的材料模型的源代码。可能是自己创建的，或者在教科书或期刊论文中找到的。这时，使用外部材料特征可能比将它转换为新形式并将其作为 ODE 集输入更高效。即使代码是用 Fortran 或 C++ 编写的，通常也可以直接将其封装到外部材料使用的 C 接口中。
编码实现可能比使用用户定义 或额外的 PDE 选项在计算上更高效。原因是关于材料定律的详细知识使得设计有效的应力更新成为可能，例如使用本地时间步进。
你可能希望以编译的形式分发您的材料模型，使最终用户无法访问源代码。事实上，第三方产品 PolyUMod 就是用这种方式实现的。
下一步
- 下载本博客中的示例源代码和模型文件(linear_hardening.mph, linear_hardening.c, linear_hardening.dll) 并获得更多关于如何使用外部材料的详细信息:
- 阅读之前的博客文章：在结构力学仿真中访问外部材料模型
- 阅读以下书籍，了解更多关于塑性计算的信息:
- J.C. Simo and T.J.R. Hughes, Computational Inelasticity, Interdisciplinary Applied Mathematics, Vol. 7, Springer-Verlag, 1998.
- M. Kojic and K.J. Bathe, Inelastic Analysis of Solids and Structures, Computational Fluid and Solid Mechanics, Springer-Verlag, 2005.
- T. Belytschko, W.K. Liu, and B. Moran, Nonlinear Finite Elements for Continua and Structures, Wiley, 2000.
PolyUMod 软件是由 Veryst Engineering LLC 开发的。COMSOL AB 及其子公司和产品与 Veryst Engineering LLC 没有关系，也没有得到 Veryst Engineering LLC 的认可、赞助或支持。
评论 (0)