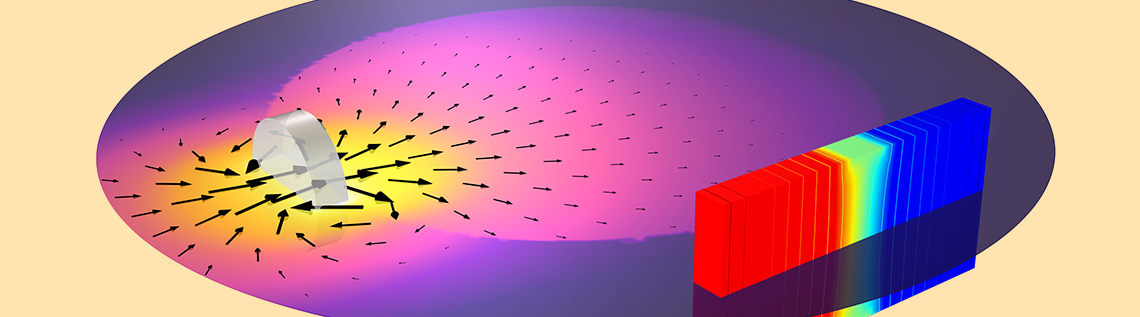
霍尔效应传感器通常用于位置检测,它的基本工作原理是附近的磁场使通过半导体传感器的电流路径发生偏转。电流的这种偏转会导致电位变化,这种变化是可以测量的。尽管这种设备具有多物理场特性,但通过几个假设,我们就可以在 COMSOL Multiphysics® 软件中非常简单地对它进行建模。阅读今天的博客文章,了解更多详细信息。
霍尔效应传感器的基本工作原理
我们从洛伦兹力的定义开始建模准备。洛伦兹力的定义是带电粒子在电场 \mathbf{E} 和磁场 \mathbf{B} 中以一定的速度 \mathbf{v} 移动的总力。粒子电荷 q 上的总力为:
假设有一块半导体材料,在其两端施加电势差,产生电流流动。对于一个均匀的平板,电流将在两端之间沿直线流动。然而,由于存在洛伦兹力,半导体材料附近的任何磁场都会使平板中的电流路径发生偏转,从而改变平板内的电势分布,这可以被测量。对于典型的霍尔效应传感器,磁场是由附近的磁铁引起的。
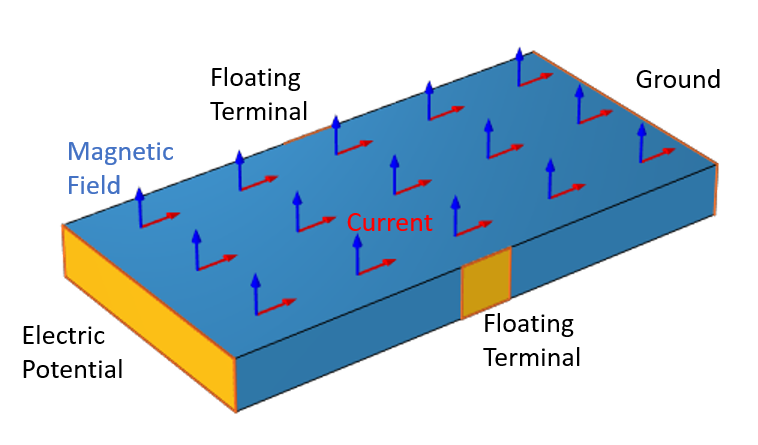
一块半导体材料。通过材料的电流会被磁场偏转,从而改变两个浮动端子之间的电位。
根据上述方程,将通过半导体材料的电流密度和两个额外的材料常数:电导率 \sigma 和霍尔系数 R_H 写为与电场和磁场相关的函数,获得在计算模型中使用的方程:
我们可以将上面的等式重写为矩阵向量乘法:
也就是说,我们可以简单地通过定义作为磁场函数的各向异性电导率来模拟霍尔效应。为简洁起见,我们将省略符号约定和对不同材料中霍尔系数推导的讨论。这是我们需要纳入到计算模型中独特的本构关系。
在最简单的情况下,我们可以只假设一个给定的磁场,用它来计算电导率,但我们在这里要做的是计算变化的磁场,并用它来创建一个真正的多物理场模型。
不过,在我们开始任何建模之前,我们将做一些假设来简化建模。假设磁场随时间的变化足够慢,可以忽略不计。也就是说,尽管麦克斯韦-法拉第方程指出:
但我们在此处假设 \frac{\partial \mathbf{B} }{\partial t} 可以忽略不计。
这各假设相当于半导体板中没有因磁铁的运动而产生明显的感应涡流。也就是说,材料中的电场仅由施加的电势和上述本构关系引起,而不是直接由任何随时间变化的磁场引起。通过这个假设,我们将问题简化为求解静磁场。
接下来,我们还将假设流过半导体的电流足够小,与磁铁产生的磁场相比,这些电流本身不会产生任何明显的磁场。这就将静磁问题简化为所谓的无电流形式,即我们只需要求解磁标量势。但是请注意,这些假设对于我们将要做的事情不是必需的。我们还可以求解由电流引起的磁场,例如来自附近线圈的磁场,但这只会使我们的模型的计算成本变高。
最后,我们还将假设材料的电导率足够大,使得 RC 时间常数比我们感兴趣的任何时间变化要短得多。也就是说,我们可以在任何时刻将电流模型看作纯静态,因为我们已经假设所有的时间导数项都不重要。因此,电学问题被简化为求解稳态电势方程,尽管随空间变化的电导率是磁场的函数。
到这里,我们已经准备好开始我们的建模了!
在 COMSOL Multiphysics® 中建立模型
假设在下图中,一个小的圆柱形磁铁被安装在一个旋转的铁轮辋上,轮辋下面有一个代表传感器的矩形域。
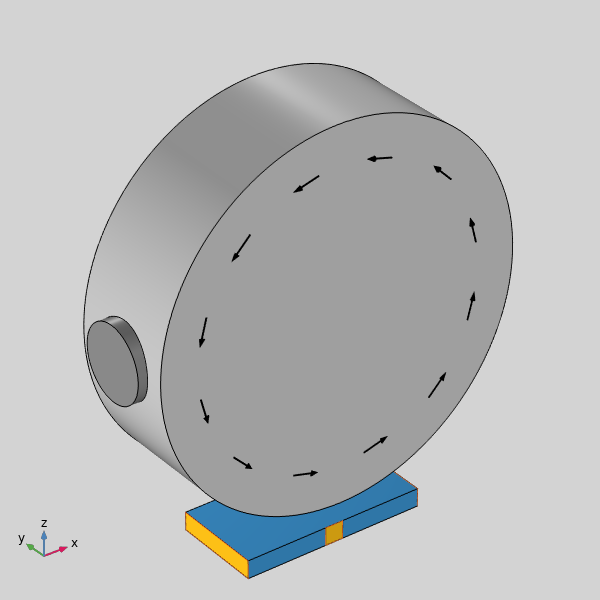
放置在旋转铁轮下方的霍尔效应传感器示意图,在轮辋上安装有磁铁。
我们首先使用 磁场,无电流 接口求解磁场。除了上图所示的域之外,我们还对围绕这些域的空气空间以及无限元 截断域进行建模。
为了求解这个问题,我们先计算磁场。然后继续研究霍尔效应传感器的模型。在半导体域,我们使用 电流 接口。为材料的两端施加 接地 和终端 条件, 其余边施加了两个 悬浮电位 条件。
有关电流 接口快速使用用法,请参阅我们的电阻设备建模系列教程视频。
电导率可以作为我们刚刚计算的空间变化磁场的函数,同时我们也想考虑车轮的旋转。考虑旋转的最简单方法是执行一个参数化扫描,但这实际上会比我们需要做的要多一点。磁场通过传感器旋转,但我们假设它们不受传感器本身的影响。
这时,根据上一篇博文中的描述,我们可以通过广义拉伸算子,使用旋转映射来改变磁场作为全局参数 Angle 的函数。但是由于我们旋转了一个矢量场,我们也要通过3D 旋转矩阵来旋转矢量本身。下面的两个屏幕截图显示了软件的操作过程,并定义了一组旋转的磁场变量。
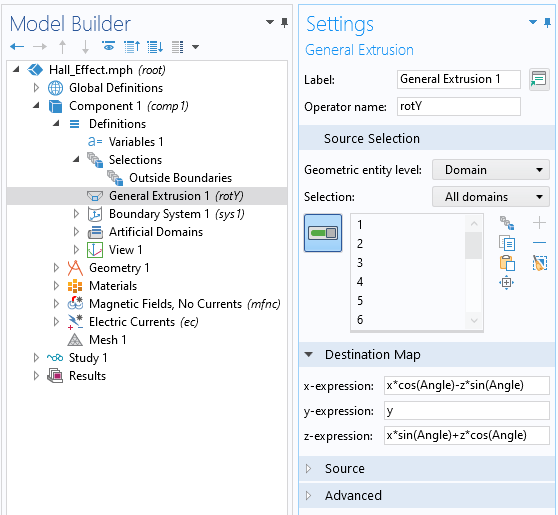
通过广义拉伸算子定义绕 y 轴的旋转。
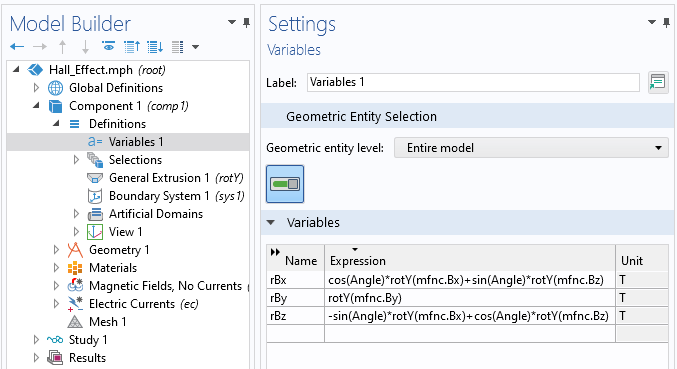
定义旋转磁场分量的变量。
定义完旋转的磁场分量,我们就可以使用它们来定义电流 接口中的电导率张量,如下面的屏幕截图所示。
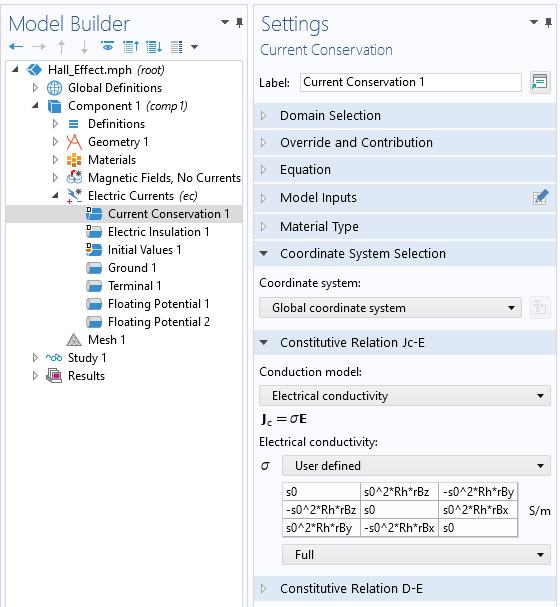
定义霍尔效应传感器内的各向异性电导率。
定义好电导率,我们就可以求解模型。我们可以分两步求解,首先求解稳态磁场,然后求解稳态电流,但要通过辅助扫使磁场描旋转不同角度,如下面的屏幕截图所示。
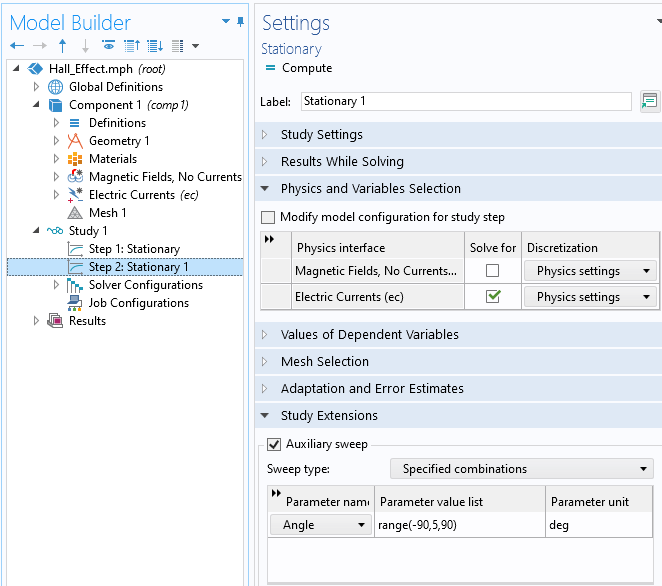
求解器的设置。第一步计算磁场,第二步计算不同磁场旋转角度下传感器中的电势。
求解模型后,我们可以为旋转场设置动画,以确认我们的方法,并检查传感器两侧的两个浮动电势边界条件之间的电势差图。
通过霍尔效应传感器的磁铁和磁场旋转动画。
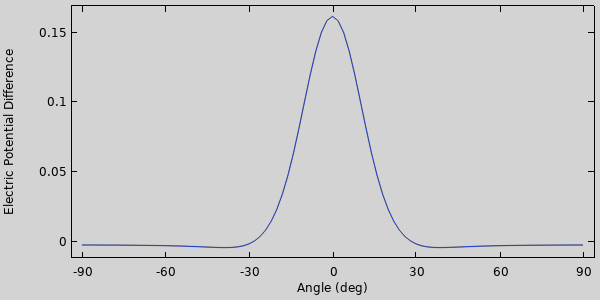
传感器上两个悬浮电位之间的电势随磁场旋转角度的变化。
动手尝试
在今天的文章中,我们展示了一种简单的模拟霍尔效应传感器的方法。能够将各向异性电导率转换为模型中任何其他变量的函数,并输入模型中的能力,使得这种模拟非常容易。通过一组变换手动旋转场,我们还可以大大降低计算成本。文中演示的模型教程可通过以下链接下载。



评论 (4)
Maokang Shen
2023-12-05Walter Frei 博士,您好!我想请教下,如果我的模型有两层,其中一层是铁磁金属,另一层是普通金属,模拟反常霍尔效应,怎么给每层加不同的本构关系(电阻率)啊?我目前只能给两层加同一个电阻率。期待您的回复!
Qihang Lin
2023-12-08 COMSOL 员工这种存在材料不同的情况我们建议您再几何上画出两层,然后直接在材料中进行设置。
建国 习
2024-12-27Hi Dr. Frei
I am an engineer in TMR sensor, and recently I create a model to simulate the TMR sensor using bottom electrode,magentoresistance junctions, top electrode, isolation layer, Cu layer, Cr layer, and permalloy layer. When running this simulation under ec modulus and cir modulus, I encounter one problem like that:
Feature: Steady-state solver 1 (sol1/s1)
Solution cannot be found for the initial parameters.
Current
Singular matrix.
For mesh instance 0, there is 1 empty equation (empty row in the matrix for variable comp1.ec.term5.V0_ode).
Located at coordinates: (0,0,0), …
For mesh instance 0, there is 1 empty equation (empty row in the matrix for variable comp1.ec.term8.V0_ode).
Located at coordinates: (0,0,0), …
Similar to degrees of freedom (empty columns in the matrix).
In Current:
The returned solution did not converge.
Not all parameter steps were returned.
Could you help me to solve this problem? If you need, I can show you this model(.mph)?
hao huang
2025-01-03 COMSOL 员工您好
感谢您的评论。
涉及到具体的仿真问题可以联系 COMSOL 的技术支持团队:
在线支持中心:cn.comsol.com/support
Email: support@comsol.com
谢谢!