
粘弹性形变广泛存在于众多的聚合物和生物组织中,即使外部载荷恒定不变,形变也会随着时间逐渐变化。线性粘弹性是一种常用近似,假设应力与应变和应变速率之间满足线性关系。我们通常认为形变的粘性部分具有不可压缩性,因此物质的体积形变近乎纯弹性。除了线性粘弹性之外,COMSOL Multiphysics® 5.2a 还能精确地模拟大应变粘弹性。下文将通过一个生物医学中的应用说明如何使用这种材料模型。
动脉的力学性能
动脉血管负责将富氧血液从心室输送到全身,其管壁由内膜、中膜、外膜(位于最外侧,又称血管外层)组成。其中,中膜和外膜是主要负责维持动脉正常力学性能的血管层。
上述两层膜的组成成分都是胶原软组织,此类组织会表现出明显可见的应变硬化行为。由于胶原纤维含量大,中膜与外膜均呈现出各向异性的特性,这表明了纤维增强结构提升了血管承受大应变的能力。
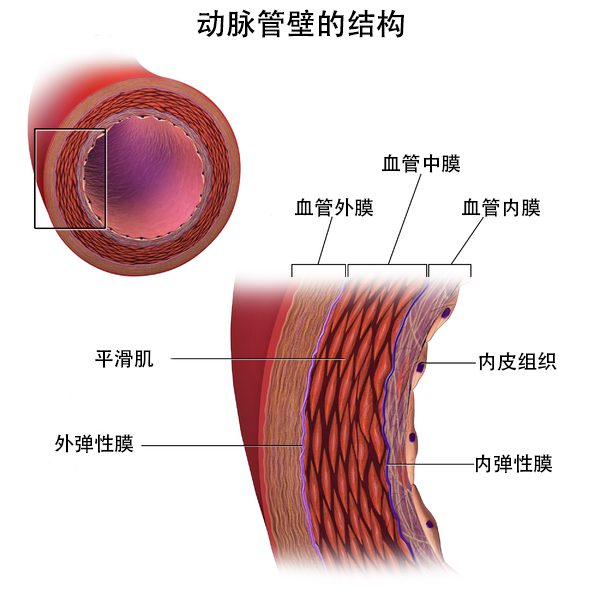
动脉管壁的结构。图片由 BruceBlaus 自行拍摄。已获 CC BY 3.0 许可,摘自维基共享资源。
在研究由年龄和疾病引起的动脉系统变化时,一个可靠的动脉壁力学本构模型是不可或缺的研究工具,而且此类工具还可应用于医学假体的设计(参考文献 3)。Holzapfel-Gasser-Ogden(HGO)本构模型(参考文献 2)能捕获上文提及的各向异性力学响应,这种力学响应已被研究人员在动脉切除实验中的观测结果所证实。在典型的实验中,研究人员测量了多段动脉对管壁的轴向拉伸行为和动脉内血压的响应,本文的数值仿真示例尝试匹配此数据,以便更准确地了解动脉的力学性能。
大应变粘弹性的理论
Bower 在《应用固体力学》一书中指出:“相比于有限应变塑性理论,有限应变粘弹性理论还不成熟,目前尚没有一个统一的公式对其进行描述。”COMSOL Multiphysics 5.2a 版本为用户提供了 Holzapfel 模型,它不仅可用于模拟大应变粘弹性(参考文献 1,参考文献 3),而且十分适合与 COMSOL® 软件中的任意预定义超弹性材料模型进行耦合。
该书的作者提出了一种广义的 Maxwell 模型,将应变能密度分解为了体积贡献和等体贡献。
其中,C 表示右 Cauchy-Green 形变张量,\bar{C} 表示等体积形变张量。\Psi_m 表示与非平衡态相关的自由能,它与等体积右 Cauchy-Green 张量 \bar{C} 和表示内部应变的变量 \Gamma_m 之间存在函数关系(参考文献1,参考文献3)。
在纯弹性分支中,应变能通带有上标 \infty,表示长时间的平衡状态(当 t\rightarrow \infty 时)。
据此,Holzapfel 模型推导出了当 t\rightarrow \infty 时,超弹性和粘弹性分支中的第二 Piola-Kirchoff 应力的表达式
并从热力学层面上对辅助应力张量进行了定义
由此,我们得出了超弹性和粘弹性分支中的总第二 Piola-Kirchoff 应力的表达式
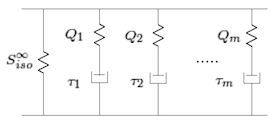
示意图展示了广义 Maxwell 模型中大应变粘弹性的第二 Piola-Kirchoff 应力。
接着,通过求解速率方程式,可以计算出粘弹性分支中应力的变化
其中,\tau_m 表示粘弹性分支的松弛时间,{S}_{iso,m} 表示此分支中的第二 Piola-Kirchoff 应力张量。
Holzapfel 模型还假设在每个分支上都具有与弹性相关的等体积应变能量密度
W_{iso, m}(\bar{C}),由此得出
Holzapfel 形式中最主要的假设是:每一个分支的等体积应变能均取决于主超弹性分支的等体积应变能
其中,无量纲系数 \beta_m>0 被称为应变能量因子。
所以,每个分支的第二 Piola-Kirchoff 应力可推导为
需求解的应变速率变成了
在 COMSOL Multiphysics 5.2a 版本中,广义 Maxwell 粘弹性模型适用于所有的超弹性材料,而且软件中用于模拟热效应的选项与模拟线性粘弹性的选项相同。
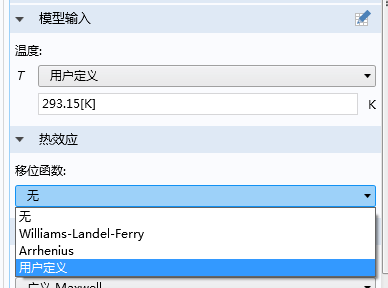
借助“用户定义”选项,可以忽略热效应,使用预定义的 William-Landel-Ferry 函数和 Arrhenius 移位函数,或者您还可以自定义移位函数。
下面,让我们来看看如何在生物力学的建模过程中应用大应变粘弹性。
在 COMSOL Multiphysics 中模拟大应变粘弹性
对于模拟动脉壁在轴向应力突然变化后的行为而言,超弹性材料模型比 HGO 材料模型更加精确,因此我们选用了前者。
如您想了解有关各向异性超弹性材料更详细的建模步骤,请查看动脉壁力学的教学模型。
首先,我们向示例材料模型中添加粘弹性行为。如参考文献 3 所述,将带有五个分支的广义 Maxwell 模型添加到 HGO 模型中,适用于模拟 1 毫秒至 10 秒范围内的松弛时间,而且还可以定量描述动脉周边的粘弹性响应(参考文献 3)。为此,我们右键单击超弹性材料 节点,然后添加一个粘弹性 节点(我们也可以将该节点与热膨胀或其他效应进行耦合)。
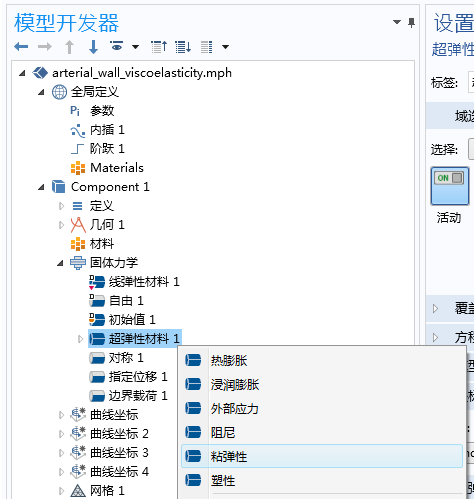
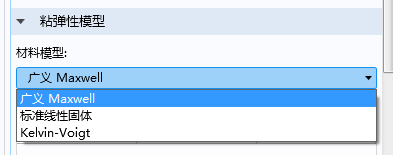
默认情况下,我们得到的是带一个分支的广义 Maxwell 模型。或者,我们也可以使用标准线性固体(standard linear solid,简称 SLS)模型或 Kelvin-Voigt 粘弹性模型。
接下来,按照参考文献 3 中的方法,在模型中添加五个分支及各自对应的能量因子和松弛时间。我们可以从文本文件中获取(或者保存)这些参数。
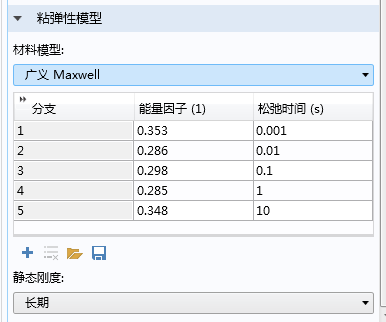
完成了对 HGO 超弹性材料添加五个粘弹性分支后,现在我们便可以开始模拟动脉截面在经受了四分钟轴向应变(大小恒定)后的情况。

粘弹性分支中的应力。请重点留意广义 Maxwell 粘弹性材料的五个分支中的应力各自对应的松弛时间。
经受轴向应力后松弛至稳定状态的时间比最高的松弛时间还长。上述示例表明了,COMSOL Multiphysics 提供了针对大应变粘弹性的模拟功能,让我们可以十分方便地研究和理解各类生物医学材料。
后续步骤
- 尝试自己动手操作:下载动脉壁管中的线弹性教学模型,学习相关知识
- 阅读相关博客文章,了解如何将线性粘弹性应用于降低弹性结构阻尼器中的振动
参考文献
- G. Holzapfel, Nonlinear Solid Mechanics: A Continuum Approach for Engineering, John Wiley & Sons, 2000.
- G. Holzapfel, T. Gasser, and R. Ogden, “A New Constitutive Framework for Arterial Wall Mechanics and a Comparative Study of Material Models,” J. Elasticity, vol. 61, pp. 1–48, 2000.
- G. Holzapfel, T. Gasser, and M. Stadler, “A Structural Model for the Viscoelastic Behavior of Arterial Walls: Continuum Formulation and Finite Element Analysis”, European Journal of Mechanics A/Solid, vol.21, pp. 441–463, 2002.






评论 (2)
建华 金
2017-06-06good
宇航 秦
2017-06-06金建华,您好!
感谢您的关注与支持!