如何模拟周期性微流体系统

在微流体系统中，流体流动始终为层流。这既是优势也是缺点，优势在于流场是稳定的，而缺点在于物质混合主要依靠扩散的方式，因此可能很耗时。在微流体芯片中混合化学物质的一种简单方法是使用蛇形通道结构。在 COMSOL Multiphysics^® 软件中，可以利用这种结构的周期性来确定所需的通道长度，从而确保化学物质在离开系统时得到充分混合。

使用 COMSOL Multiphysics^® 模拟周期性微流体系统

下图为一个具有蛇形通道的微流体装置示例。化学稀物质溶液可通过两个入口进入系统，两股流体汇合后流经蛇形通道。由于微流体系统中的流动是层流，因此化学物质的混合是通过扩散实现的。为了高效地模拟系统，我们可以利用结构的周期性，考虑模拟一个基本单元。

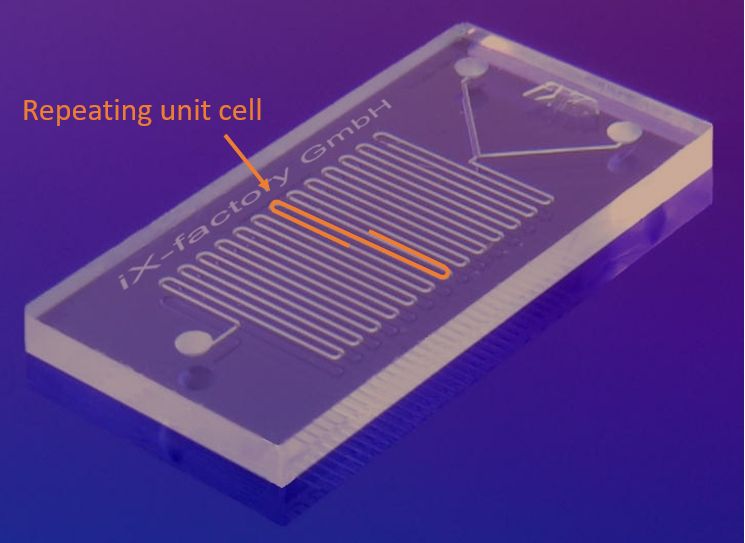
一个典型的微流体装置。图片经过修改。原图由 IX-factory STK — Own work 提供，获 CC BY-SA 3.0 许可，通过 Wikimedia Commons 共享。原作品已被修改。

我们在之前的两篇博客中也讨论过这个蛇形通道。第一篇博客，使用广义拉伸算子模拟周期性结构通过求解一个基本单元中的层流减少了计算量，并使用 广义拉伸 算子将速度场映射到包含多个单元的完整几何结构。如下图所示，完整几何结构上的稀物质传递使用映射的速度场求解。

模拟周期性微流体装置的第一种方法。计算一个基本单元中的速度场，并将其映射到完整的几何结构上，以计算完整几何结构中的浓度分布。

在第二篇博客利用含高佩克莱特数模型中的周期性中，该模型得到进一步简化，重点研究具有高佩克莱特数的微流体系统。在这种情况下，物质传递主要依靠对流而不是扩散的方式，下游溶液不会影响上游溶液。因此，没有必要像第一种方法那样计算整个装置上的物质传递。

对于高佩克莱特数，可以逐个单元地按顺序计算物质传递。如下图所示（“方法 2”），计算一个基本单元中的速度场，然后求解浓度场。利用 广义拉伸 功能，将出口处的浓度场映射到入口处。为确保在下一次迭代中使用上一个解进行浓度映射，需要使用 边界常微分和微分代数方程 接口以及 上一个解 功能。

今天这篇博客，我们将介绍能够实现相同目标的另一种方法，即将结果从出口传递回入口，按顺序计算物质传递。使用状态变量代替边界常微分方程。状态变量比边界常微分方程更容易实现，可以降低模型的复杂性。

第二种和第三种方法仅使用一个单元模拟周期性微流体装置。这两种方法的不同之处在于步骤 3。从出口到下一个基本单元入口的浓度分布映射，可以使用边界常微分方程或状态变量来实现。(下文我们将解释第三种方法）。

广义拉伸和状态变量

首先，在出口边界上定义广义拉伸 算子 genext1。该算子可在 定义>非局部耦合 节点下找到，它通过指定 x 轴上的位移，将一个表达式（在本例中为浓度）从出口映射到入口。

通过在 x 轴方向偏移 6 mm，广义拉伸算子将变量从一个边界映射到另一个边界。

第二步，在入口边界上定义状态变量 。状态变量 功能位于 定义>变量实用程序 节点。在模型中，状态变量被视为因变量。与物理场接口中常见的因变量不同，状态变量可以设置为在每个收敛的参数步或时步之前与之后更新，或者仅在初始化时更新。状态变量的设置如下图所示，状态变量名为 c_b。作为一个初始值，阶跃函数用于显示入口处的初始浓度梯度。阶跃函数位于 x = 0.5 mm 处，根据其在 x 轴位置的不同，初始浓度在 0 ~ 1 mol/m³ 之间变化。状态变量总是在参数阶跃开始时更新，这意味着，上一步出口处的浓度将被映射到下一步迭代的入口处。

状态变量的 设置 窗口。

状态变量 c_b 作为 稀物质传递 接口中 流入 边界的浓度。状态变量的数据被存储在高斯点，而不是网格节点。因此，选择 通量 (Danckwerts) 作为 边界条件类型 ，而不是 浓度约束。在网格节点施加浓度条件，Danckwerts 条件则在高斯点施加通量。

状态变量 c_b 被设置为流入边界的浓度。

为尽量减少外推误差，在入口和出口边界使用了 相同网格 功能。

相同网格 功能的 设置窗口。边界 2 和边界 7分别为入口和出口边界。

与之前的博客类似，我们分两步计算模型。研究步骤设置如下图所示。在第一个研究步骤中，只对一个基本单元计算 层流 接口。无论基本单元重复多少次，流场都是相同的，但物质传递并非如此。第二步，计算 稀物质传递 和 状态变量。此外，我们还引入了一个参数 n_unit_cells，按顺序计算重复单元。该参数用于辅助扫描，并从 1 开始以 1 为增量扫描至最大单元数，本例中为 15。每次计算结束后，都会更新状态变量，并将出口处的浓度场映射到后续基本单元的入口处。为了正确更新状态变量，将 运行继续运算 设置为 无参数，并将 重用上一步的解 设置为 是。

启用 辅助扫描 功能后的研究步设置。参数 n_unit_cells 代表基本单元的数量。

最终，我们得到所有重复单元的浓度分布图。下图显示了前三个基本单元。

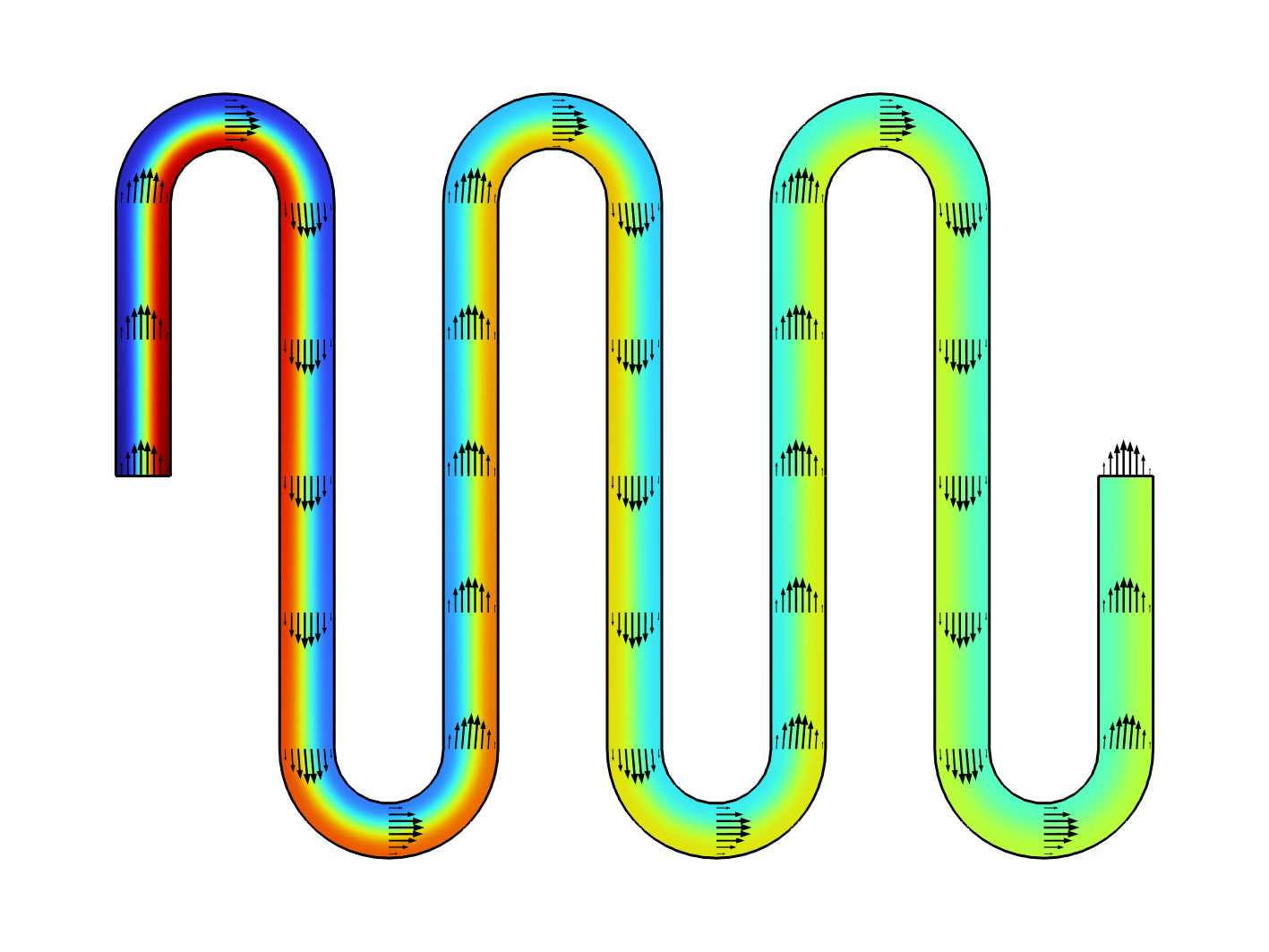
前三个基本单元的浓度分布。

本文介绍的模拟结果可用于确定混合程度和所需的通道长度。采用辅助扫描方法，我们能够高效地任意扩大混合器的规模。为了进一步衡量系统的混合程度，可以考虑混合指数（MI）。混合指数是在整个通道横截面上计算得出的，其定义如下：

其中， \textless{c}\textgreater 表示出口边界的平均浓度，{\sigma} 表示其标准偏差。

混合指数与基本单元数量的函数关系。

图中显示了重复 15 次后每个基本单元出口处的混合指数。重复 5 个基本单元后，混合指数已达到 0.98。

结束语

本文讨论的方法与博客利用具有高佩克莱特数模型中的周期性中讨论的方法非常相似。这些方法简化了模型，节省了计算资源。它们与之前方法的主要区别在于，使用状态变量保存出口浓度并将其传递到下一次迭代，而不是使用 常微分方程。使用状态变量的方法更容易实施，因为不需要改变求解器的配置。因此，我们建议使用状态变量法模拟具有高佩克莱特数的系统。这种方法也可以用于更复杂的应用，例如物质之间会发生反应的多种化学物质的混合。

延伸阅读

想了解更多文中提到的有用功能吗？请阅读以下博客：

• 深入学习如何使用高斯点功能：数值积分与高斯点简介
• 了解有关 状态变量 功能的更多信息：如何在 COMSOL Multiphysics^® 中使用状态变量
• 查看如何使用 广义拉伸 算子：用广义拉伸算子映射变量
• 了解更多关于 广义拉伸 算子的用法：广义拉伸算子的一些示例