借助 COMSOL® 仿真 App 执行弱形式

在之前的弱形式系列博客中，我们对弱形式方程进行了离散，希望得到可用于求解我们简单示例问题中未知系数的矩阵方程。按照博客“在 COMSOL Multiphysics 中执行弱形式”中的步骤操作，我们将能在 COMSOL Multiphysics® 软件中执行该方程，并能加入其他步骤来检查矩阵。我们还发现可以借助 COMSOL® App 更轻松地实现所有相关矩阵的同时展示，并能在同一个屏幕上按类排列。

简单示例

请回想之前稳态无热源的一维传热示例，其中温度 T 是定义在区间 1\le x\le 5 求解域中的关于位置 x 的函数。 我们将左边界 (x=1) 设为诺伊曼边界条件，指定向外通量为 2，并将右边界 (x=5) 设为狄氏边界条件，以便将温度设为 9。对弱形式方程进行离散化，得到该矩阵方程：

(1)

其中 a_1, a_2, \cdots , a_5是节点 (x=1, 2, \cdots, 5) 处的未知温度值，\lambda_2是右边界(x=5) 处的未知热通量。由于该方法最早应用于结构力学问题，左侧的矩阵通常被称作刚度矩阵，右侧的矢量常被称为载荷矢量。

查看刚度矩阵和载荷矢量

“在 COMSOL Multiphysics 中执行弱形式“博客讨论过在 COMSOL Multiphysics 中执行弱形式方程的步骤，因此本文将不再重复。如希望查看刚度矩阵和载荷矢量，右击模型树中的解 1 → 其他 → 组装，如下图所示：

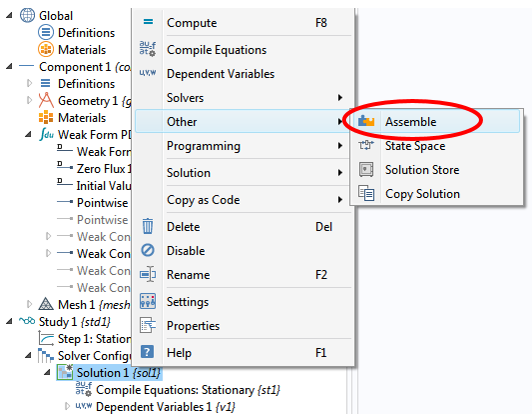
务必将组装节点拖动到稳态求解器之上。之后，在组装 1节点的设定窗口中，我们可以勾选感兴趣矩阵前的复选框选。此外，将因变量 1 的缩放比例设为无。求解后，我们可以右击派生值，然后选择系统矩阵，如下图所示：

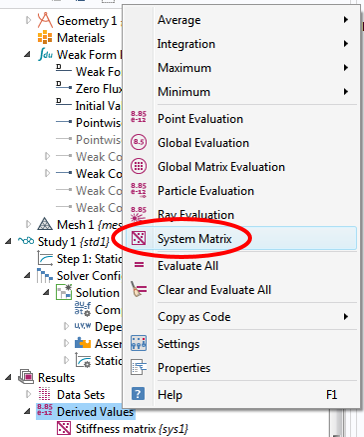
在对应的设定窗口中，我们可以从矩阵的下拉列表中选择刚度矩阵，并在表中计算。如下图所示，我们可以精确获取如方程 (1) 所示的相同 6*6 矩阵。

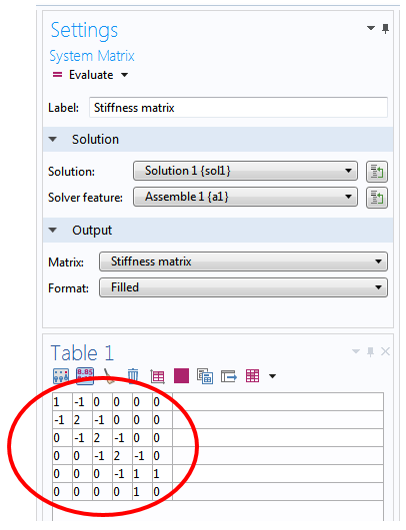
可以采用相同的步骤对方程 (1) 右侧的载荷矢量进行计算和验证。

逐点约束

我们之前提到过有时不必求解拉格朗日乘子 \lambda_2，比如说为了节省计算资源。如希望这样操作，可以选择右击弱解型偏微分方程主节点 → 更多 → 逐点约束，如下所示：

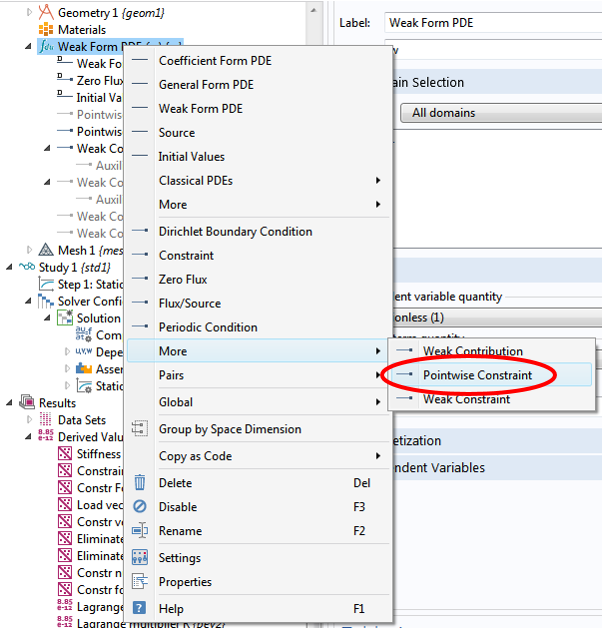
之后，在设定窗口的约束表达式输入框中输入 9-T。求解完成后，我们将得到完全相同的解，但将得到一个较小的 5*5 刚度矩阵：

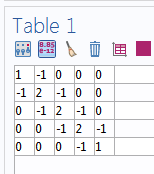
如仔细分析这一矩阵，我们将发现它与之前分析的 6*6 矩阵的左上角相匹配。这并不奇怪，因为我们正在求解同一个问题（由方程 (1) 表征），只是换了一种略微不同的方式。我们接下来将对此进行简要介绍。

另一种求解矩阵方程的方法

如“在 COMSOL Multiphysics 中执行弱形式”博客的介绍，当使用含拉格朗日乘子 \lambda_2 的弱贡献特征执行狄氏边界条件时，我们希望能有效求解整个矩阵方程 (1)，从而得到系数 a_1, a_2, \cdots , a_5 和乘子 \lambda_2。

另一方面，当使用如上所示的逐点约束特征执行固定边界条件时，我们其实希望能在不对拉格朗日乘子\lambda_2 进行显式求解的情况下，求解同样的矩阵方程 (1)。软件可以高效地将方程 (1) 分隔为这种形式（见下方）

(2)

其中刚度矩阵 K 是上方所示的 5*5 矩阵，约束雅可比矩阵 N 是 (0 \, 0 \, 0 \, 0 \, 1)，约束力雅可比矩阵 N_F 是 (0 \, 0 \, 0 \, 0 \, 1)^T，解矢量 U 由系数 a_1, a_2, \cdots , a_5 组成，单元矢量 \Lambda 由拉格朗日乘子 \lambda_2 形成，载荷矢量 L 为 (-2 \, 0 \, 0\, 0\, 0)^T，单元约束矢量 M 是 (9)。

下图显示了对方程 (1) 的偏析：

当然在实际操作中，指定逐点约束特征后，软件将不会再组装方程 (1) 中的全 6*6 矩阵。相反，它将组装 K、N 和 N_F，与组装整个矩阵相比可以占用更少的计算资源。

方程 (2) 可以写作由两个矩阵方程组构成的系统：

(3)

(4)

其中，方程 (3) 的第一项是对含热通量边界条件的离散化弱形式方程，第二项 (4) 包括由狄氏边界条件施加的约束。

方程系统可以通过两步求解。第一步，求解约束方程 (4) 以得到与狄氏边界条件相关的自由度。第二步，将第一步的解带入方程 (3)，求解剩余的自由度。

得到的解矢量 U 随即作为两步解的线性组合：

(5)

第一项 U_d 是第一步中求解的约束方程 (4) 的解矢量。第二项从第二步中获取，形式为矩阵 Null 和解矢量 U_n 的乘积。NULL矩阵中的列由生成约束雅可比矩阵 N 中零空间的基向量构成。因此得到

解矢量 U_n 是消去的矩阵方程的解

(6)

其中，消去的刚度矩阵K_c 及消去的载荷矢量 L_c 由以下得到

矩阵 Nullf 中的列由生成约束力雅可比矩阵转置 N_F 中的零空间的基向量组成。因此得到

消去的项表示从矩阵方程 (6) 中移除与狄氏边界条件相关的自由度。在我们的示例中，消去的刚度矩阵 K_c 的大小为 4*4。

注意，上述求解步骤不涉及拉格朗日乘子矢量 \Lambda。的确，这一步骤中并未求解拉格朗日乘子 \lambda_2 的值。这一方法的优势是减少了所需的计算资源。在我们的简单示例中，矩阵的大小从 6*6 降为 4*4（加上一个从约束方程中得到的更小矩阵）。

在 COMSOL® App 中查看所有矩阵

COMSOL Multiphysics 支持我们计算及查看上面提到的所有矩阵和矢量。这里只需重复查看刚度矩阵和载荷矢量节的操作步骤。但我们很快发现，需要花费大量时间来点击模型开发器中的每个系统矩阵节点和每个设定窗口中的”计算”按钮。同样，我们一次只能查看一个矩阵或矢量，因此如果要检查所有的矩阵及矢量，将相当耗时。

这就是一个很典型的场景，我们可以借助 COMSOL App 来提升我们的建模体验和生产力 (在下方的 App 网络研讨会中进一步学习)。您可以使用 COMSOL Multiphysics 的核心功能为所有 COMSOL 模型进行用户界面 (UI) 封装，开发一个 COMSOL App。UI 支持完全定制，用户可以轻松配置以满足单独的建模需求。

如希望获取对 COMSOL App 的简要介绍，您可以观看以下网络研讨会：COMSOL Multiphysics® 5.0 及 App 开发器简介（重点观看第二部分）以及如何利用 COMSOL Server™ 开发及运行仿真 App 。

以下截屏只列出了 UI 的几种排列方式，以便将其作为一个更好更简单的矩阵及矢量分析工具。通过 App 内的复选框在几种不同的边界条件间切换。只需轻击”计算”按钮就能查看及计算所有的矩阵和矢量。下图显示了需要求解全 6*6 矩阵时的情况：

我们看到 N, N_F 和 M 为空，K_c 为全尺寸的 6*6 矩阵。相比之下，下图为第二种情况，用消去的 4*4 矩阵求解：

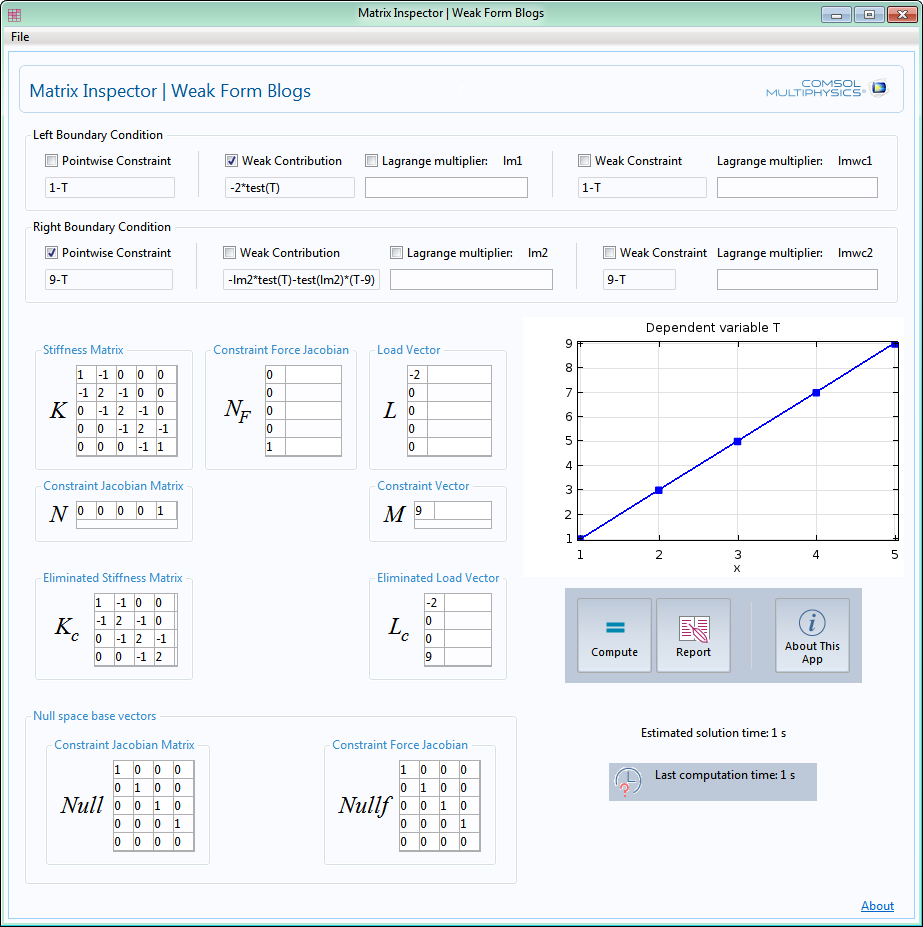
结束语

借助我们简单的传热示例，我们探索了用于求解通过离散弱形式方程得到的矩阵方程的两种方式。我们发现通过开发 COMSOL App，可以更轻松地计算与检查各种矩阵及矢量。在后面的博客中，我们将继续使用 COMSOL App 来分析更复杂的示例。

作为一个通用性多物理场仿真开发环境，COMSOL Desktop® 环境提供的 UI 元素有限。COMSOL App 则帮我们解决了这一局限，使我们能针对特殊要求定制 UI。此外，内置的编码功能还支持更加多用途的计算，COMSOL Server™ 许可证使我们能够向遍及全球各地的同事及客户部署 App。

我们希望 COMSOL Multiphysics 中的这些强大功能可以帮您实现工作效率的提升。