
我们都知道, COMSOL Multiphysics 可以求解偏导数。毕竟,它是通过有限元方法求解偏微分方程。那么,您知道它也可以求解积分吗?这一点并不太会令人惊讶,因为求解有限元问题需要对函数进行积分。COMSOL 软件架构允许您做的不仅仅是计算一个积分;您还可以求解未知积分限的问题!下面让我来介绍方法。
对函数进行积分
考虑一个求解二次函数积分的问题:
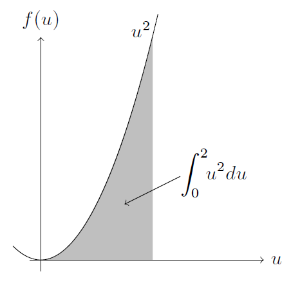
积分可以获得阴影区域的面积。
我们可以在 COMSOL Multiphysics 中使用积分函数来计算这个积分,这个函数的语法为:integrate(u^2, u, 0, 2, 1e-3)。其中,第一个参数是表达式,第二个参数是要积分的变量,第三和第四个参数是积分的极限,可选择的第五个参数是必须在 0 到 1 之间的的积分相对容差。如果省略第五个参数,就将使用默认值 1e-3。我们可以在模型设置中的任意位置调用这个函数。
在这里,我们将在 全局方程 接口中使用它:
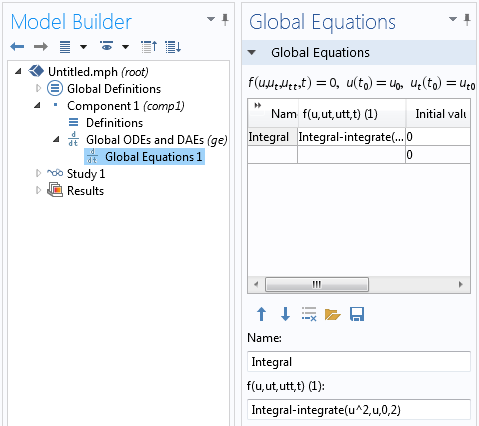
用于 积分的全局方程计算了指定极限之间的积分。
到目前为止,这里没有什么太大的惊喜。我们可以在 COMSOL Multiphysics 中求解这个问题,或者手算得到结果。但假设我们把问题稍微想复杂一点,如果我们知道积分的计算结果,但不知道积分的上限怎么办?
我们来看看如何求解下面这个 u_b 的上限问题:
我们可以通过改变全局方程来求解这个问题,这样就可以得到积分上限:
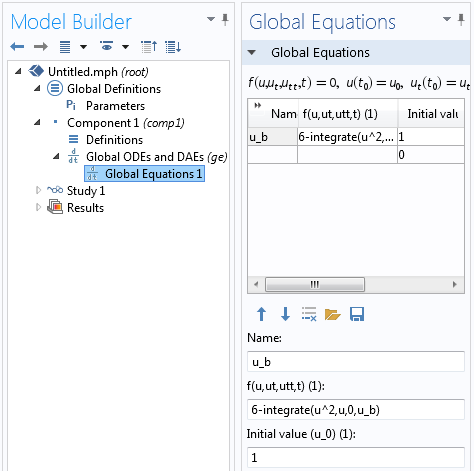
u_b 的全局方程求解了积分的上限,计算结果为 6。
上面的全局方程有一些变化。其中的变量更改为 u_b,必须等于零的表达式变为:6-integrate(u^2, u, 0, u_b)。因此,软件将找到一个 u_b 值,使积分等于指定的值。
请注意,u_b 的初始值不能为零。
由于我们使用 Newton-Raphson 方法来求解这个问题,因此不应该从函数斜率为零的点开始。经过求解,我们发现 u_b = 2.621。
现在,我们让事情变得复杂一点,这次需要求解的是 u_a 和 u_b 这两个极限:
由于我们有两个未知数,显然需要在这里再加一个方程,所以让我们再假设 (u_b-u_a)-1=0。
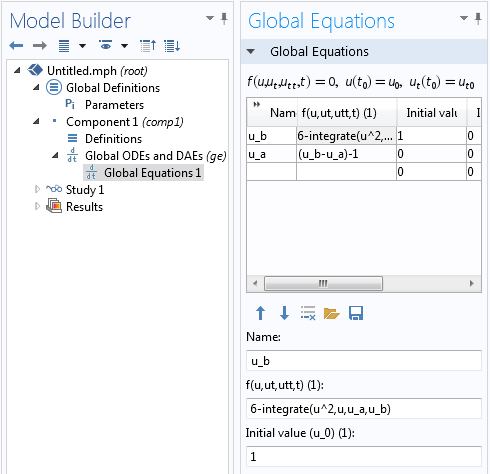
添加了一个额外的方程来指定区间上限和下限之间的差值。
求解如上所示的模型,将得到 u_a = 1.932 和 u_b = 2.932 的值。实际上也可以用单个全局方程来求解这个问题,方法是将 6-integrate(u^2, u, u_b-1, u_b) 写成求解 u_b 的方程,但有趣的是,我们可以同时求解多个方程。
一个传热示例
接下来,让我们将上文中介绍的技术用于实践,来确定换热器的运行条件。以 COMSOL 案例库中的一个示例来说明,即通过一个浸没在池塘中的管道网络循环对水进行地热加热。
通过水下管道网络泵送的水被加热。
在这个示例中,管道流模块用于模拟 5°C(278.15 K)的水被泵入管网,并被池塘中相对较温暖的水加热。池塘中的水温随深度在 10°C 至 20°C 之间变化,输出端的计算温度为 11.1°C(284.25 K)。如果水的质量流量指定为 4 kg/s,那么吸收的总热量为:
其中,\dot m 是质量流量,C_p(T) 是与温度有关的比热。
实际上,这里的管道网络是一个闭环系统,但我们根本没有对管道出口和入口之间的系统部分进行建模,这里包含一个隐含的假设,就是当水从出口泵回入口时,它被精确冷却到 5°C。
因此,与其假设进入管道的水的温度是恒定温度,不如考虑这个闭环系统连接到另一个换热器,通过它来去除指定的热量。假设该换热器只能提取 10 kW,那么管道中的水温是多少?
显然,就未知极限 T_{in} 和 T_{out} 而言,这里的第一步是写出提取热量的积分:
我们需要包括的第二个条件是输入和输出温度之间的关系,这是由我们现有的有限元模型计算得出的。现有模型在管道入口处使用一个固定的温度边界条件,并沿管道的整个长度计算温度。因此,对于提取的热量而言,我们需要做的就是在现有模型中添加一个全局方程来计算(最初未知的)入口温度,T_in,以及入口和出口之间的温差。
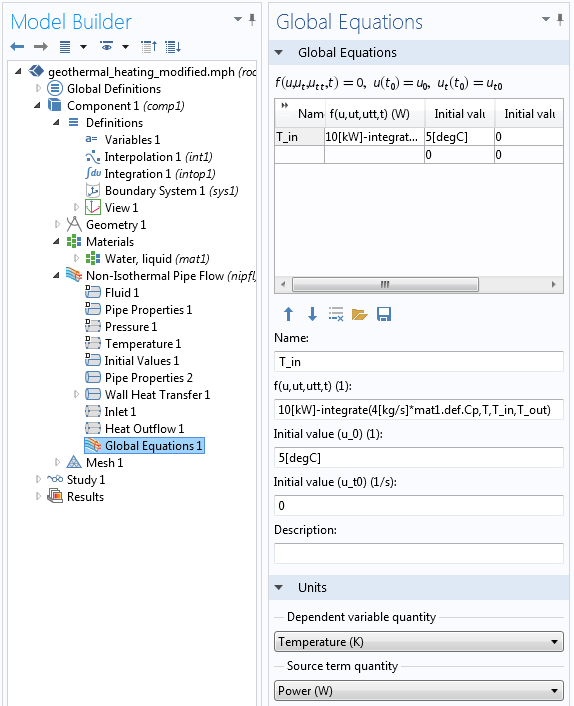
全局方程指定了从池塘回路中提取的总热量。
让我们详细看一下管道流动模型的入口温度 T_in 的方程:
10[kW]-integrate(4[kg/s]*mat1.def.Cp, T, T_in, T_out)
从右侧开始,T_out 是计算的出口温度,可以通过使用在流动管网出口点定义的积分耦合算子在全局方程计算。也就是说,T_out=intop1(T),在组件定义中设置为全局变量。
T_in 是管网入口处的温度,这是我们要计算的量;T 是温度变量,在材料定义中会使用;mat1.def.Cp 是在材料分支中定义的温度与比热的关系表达式。
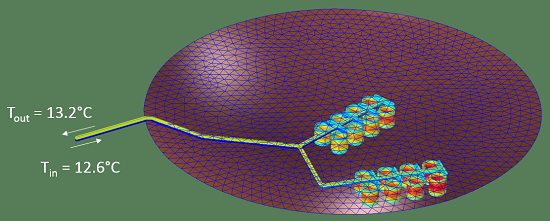
闭环解决方案,在这个工况点提取 10 kW。请注意在这些操作条件下,池塘内的水是如何加热和冷却的。
结语
从我们在文中介绍的技术中可以看出,您不仅可以进行积分,甚至可以求解该积分的极限,并使其成为模型其余部分的一部分。仔细想想,文中给出的示例考虑了换热器,您还能在哪里用到这种强大的技术呢?






评论 (0)