高频电磁场的多尺度模拟导论

本篇文章将开启一个全新的综合性博客系列，探讨高频电磁场的多尺度模拟方法。在首篇文章中，我们将介绍必要的支撑理论和定义。后续的文章将指导您如何使用 COMSOL Multiphysics® 软件在不同场景下对高频电磁场进行多尺度模拟。让我们开始吧！

应用范围：天线和无线通信

多尺度模拟是现代仿真技术的一个挑战性课题，它指的是当一个模型具有截然不同的尺度时产生的问题。举例来说，你的手机大约长 15 cm，但是它需要从 20,000 km 外的卫星接收 GPS 信息，在一个仿真中同时处理这两个长度往往并不简单。天气、化学以及许多其他领域的仿真应用也会遭遇类似的问题。

虽然多尺度模拟是一个泛泛的话题，不过我们选择将重点放在天线和无线通信的实例上。当通过天线进行无线数据传输时，传输过程可以分为三个主要阶段：

1. 天线将本地信号转换为自由空间辐射。
2. 辐射向远离天线的方向传播，经过一段相对较长的距离。
3. 另一个天线检测到辐射，并将其转换成接收信号。

现代通信通过天线进行远距离无线数据传输。

数据传输过程中的两个长度尺度是辐射波长和天线间的距离。我们想象一个具体的场景：FM 收音机的波长约为 3 m，当你坐在汽车中收听广播时，通常距离无线电塔十公里以上。许多天线（例如偶极天线）的尺寸与波长相近，因此不必将天线尺寸看作一个不同的长度尺度。综上所述，涉及的尺度包括：发射天线的长度尺度，信号从源传送到目的地的另一种长度尺度，然后又是接收天线的原始长度尺度。

在同一个高频电磁模型中处理多个尺度之前，我们先重温一些最核心的方程式、术语和注意事项。

弗里斯传输方程

弗里斯（Friis）传输方程计算的是两个由无损耗介质隔开的天线间的视距通信的接收功率，公式为

其中，下标 r 和 t 区分了发射天线和接收天线，G 是天线增益，P 是功率，\Gamma 是天线与传输线之间阻抗失配的反射系数，p 是极化失配因子，λ 是波长，r 是天线之间的距离，它与所谓的自由空间路径损耗相关联，\theta 和 \phi 是两个天线的角球坐标。

请注意，我们明确地引入了两个阻抗失配项，因此：

• P_t 指发射天线提供给传输线的功率
• P_r 指接收天线从传输线接收的功率

许多文本注明了弗里斯传输方程的推导过程，所以我们在这里略过。

发射天线和接收天线增益的可视化图像。在使用弗里斯传输方程时，我们必须了解天线的方向，才能获得正确的增益参数。天线之间的距离为 r。

球面坐标

下面，我们来讨论球面坐标 \left(r,\theta,\phi\right)，原因是球面坐标极其适用于研究天线辐射，而且我们会在下文中反复使用它们。从笛卡尔坐标（x，y，z）出发，我们可以利用很方便地得到以下表达式。

为了方便起见，我们使用了真实的 COMSOL Multiphysics 命令——sqrt()、acos() 和 atan2(,)，而不是它们的数学符号。在创建仿真时，我们还将利用球面单位矢量 \hat{\theta} 的笛卡尔分量。

\hat{r} 和 \hat{\phi} 的笛卡尔分量也能实现类似的任务，但 \hat{\theta} 对于我们来说是最重要的。在介绍射线光学的后续博客中，我们将探讨这一问题。

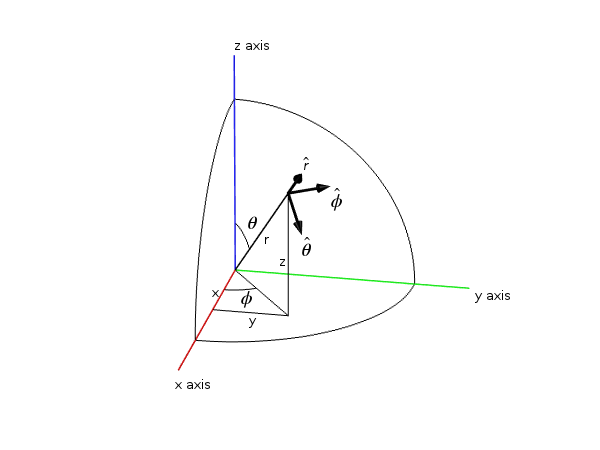
给定点同时使用笛卡尔坐标 (x, y, z) 和球面坐标 \left(r,\theta,\phi\right) 进行表示。球面坐标的单位矢量也显示在图片中。请注意，球面坐标的单位矢量是位置的函数。

坡印廷（Poynting）矢量和辐射强度

我们通常对天线的辐射功率很有兴趣。功率通量的单位为 W/m²，使用复坡印廷矢量 \vec{S}=\frac{1}{2}\vec{E}\times\vec{H}^* 来表示。

许多有关天线的文本也会使用辐射强度，其定义为每立体角辐射的功率，单位为 W/steradian（瓦/球面度）。在数学中，它的公式写作 U(\theta,\phi)=r^2\operatorname{Re}(\vec{S}\cdot\hat{r})=\frac{dP}{d\Omega}。为了让读者更清楚，我们在此引入了两个惯用法：U(\theta,\phi) 常用于电气工程，而物理学家通常更加熟悉 \frac{dP}{d\Omega}。之后，我们对所有角度上的辐射强度进行积分，由此计算出辐射功率。

增益和方向性

增益和方向性的相似之处是二者均能对特定方向的辐射功率进行量化，不同之处是增益将特定方向的辐射功率与输入功率相关联，而方向性将其与总辐射功率相关联。更简单地讲，增益能够解释电介质损耗和导电损耗，而方向性不能。在数学中，增益和方向性分别表示为 G\left(\theta,\phi\right)=4\pi\frac{U\left(\theta,\phi\right)}{P_{in}} 和 D\left(\theta,\phi\right)=4\pi\frac{U\left(\theta,\phi\right)}{P_{rad}}。P_in 是天线接收的功率，P_rad 是总辐射功率。虽然这两个物理量都有意义，但是增益可以解释天线中的材料损耗，一般情况下更为实用。考虑到它的常用性和实用性，我们还参考了“IEEE 有关天线术语的标准定义（IEEE Standard Definitions of Terms for Antennas）”，（在给定方向上）的增益定义为：“在天线接收的辐射功率为各向同性的条件下，给定方向上辐射强度与接收的辐射强度之比。”

针对增益的定义，IEEE 添加了三个注释：

1. “增益不包括由阻抗和极化失配所引起的损耗”。
2. “各向同性辐射功率的辐射强度等于天线接收的功率除以 4π”。
3. “如果天线没有耗散损耗，那么在任意给定方向上其增益等于其方向性”。

增益、实际增益和阻抗失配

在现实中，真正的天线会连接到传输线。天线和传输线的阻抗或许不一样，所以可能会由于阻抗失配而存在损耗因子。实际增益 指考虑到阻抗失配时的增益。在数学中，实际增益表示为 G_{realized} = \left(1-|\Gamma|^2\right)G，其中 \Gamma = \frac{Z_c-Z}{Z_c + Z} 为传输线理论的反射系数，Z_c 为传输线的特性阻抗，Z 为天线的阻抗。

在 COMSOL Multiphysics 中使用带特性阻抗的集总端口时，计算的远场增益相当于 IEEE（电气和电子工程师协会） 定义的实际增益。我们必须明确提及这一点，因为在过去的几十年中增益的定义发生了多次变化。从 2017 年发布的 COMSOL Multiphysics 5.3 版本起，COMSOL 软件将按照 IEEE 的定义更改变量名称。

Vivaldi 天线的实际增益和电场，使用了 COMSOL Multiphysics 和“RF 模块”进行模拟。您可以在“案例下载”中获取 Vivaldi天线的教学模型。

接收天线、洛伦兹互易定理和接收功率

到现在为止，我们讨论的术语对应的是发出辐射的天线，不过它们通常同样适用于接收天线。在上文中，我们更关注发射的原因是天线通常遵守互易定理（洛伦兹互易定理是大多数天线教科书的必要章节）。互易的含义是在特定的方向上，不管是沿此方向发射信号还是从此方向接收信号，天线的增益都是相同的。在实践研究中，您可以使用发射天线的单个仿真来计算任意方向上的增益，这比模拟每个指定方向上的接收过程更加简单。

当讨论到接收天线时，我们往往想要计算入射信号的接收功率。具体的方法是用天线的有效面积 A_e=\frac{\lambda^2}{4\pi}G 乘以入射功率通量，同时考虑到传输线的阻抗失配，由此得出 P_{rec} = \frac{\lambda^2}{4\pi}\left(1-|\Gamma|^2\right)G|\vec{S}|。不出所料，它与弗里斯传输方程的其中几项惊人地相似。

发射器示例：完美电偶极子

今天，我们将讨论一种类型的发射器：完美电点偶极子。您可能在不同的文献中看到它被称为完美、理想或者无穷小偶极子。此发射器常用于表征电小天线的辐射。场的求解方程为

其中 \vec{p} 为辐射源的偶极矩（勿与极化失配混淆），k 为介质的波矢。

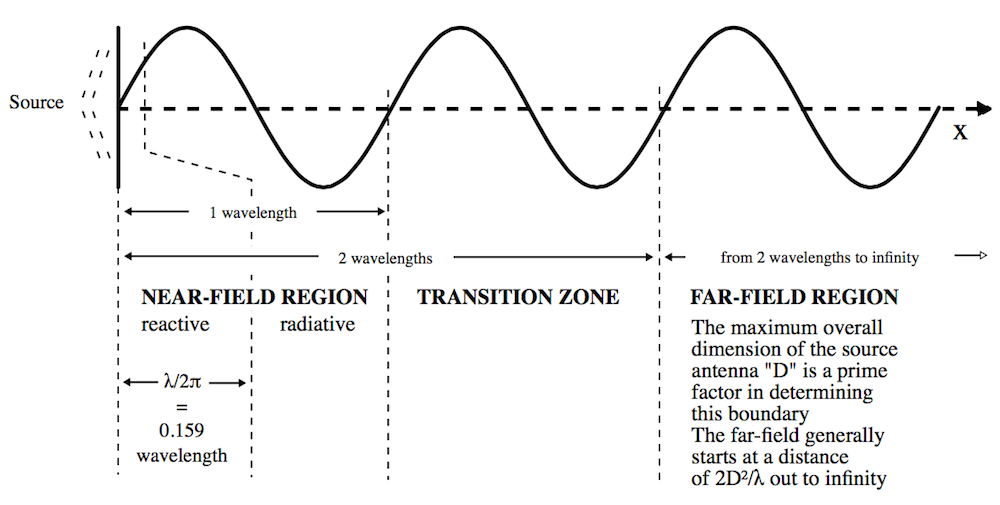
电小天线产生的电磁场的各区域分解图。

在上述方程中，1/rⁿ 有三个因子。1/r² 和 1/r³ 项在信号源附近更重要，而 1/r 项在较大的距离上占主导地位。虽然电磁场是连续的，不过人们一般会根据与源的距离来划分场的不同区域。上图显示了电小天线的一种场分布，事实上，还有其他适用于描述 kr 大小的惯用法。

之后，我们将展示如何计算与给定源相隔任意距离的场，不过天线通信的最关键区域是与源相距最远的远场 或辐射区。在这个区域内，场表现为球面波 \sim exp(-jkr)/r 的形式，之后我们会利用这个事实。

现在我们要将 E-field 方程式拆分为两个项。为简单起见，我们将 1/r 项称为远场（FF），将 1/r² 和 1/r³ 项称为近场（NF）。

如上文所述，我们可以对所有角上的 U(\theta,\phi)=r^2\operatorname{Re}(\vec{S}\cdot\hat{r})=\frac{dP}{d\Omega} 进行积分，借此计算以瓦特为单位的辐射功率。请注意，只有远场项对积分有贡献，这就是对于天线工程师而言，天线具有实际意义的主要原因。点偶极子辐射的总功率为 P_{rad} = \frac{c^2Z_0k^4}{12\pi}|\vec{p}|^2，其中 Z₀ 是自由空间的阻抗，c 是光速。最大增益为 1.5，它在垂直于偶极矩的平面（例如 \hat{z} 中偶极子的 xy 平面）中是各向同性。

关于单位的说明：我们根据单位为库仑*米（Cm）的偶极矩 \vec{p}=\int{\vec{r}\rho(\vec{r})d\vec{r}} 的传统定义写出上方的表达式。天线和工程的文本通常使用安培*米（Am）来指定无穷小电流偶极子。COMSOL Multiphysics 遵循工程惯例。上述两个定义由时间导数关联起来，因此在 COMSOL 软件中执行方程时，应该将偶极矩 \vec{p} 乘以因子 j\omega 来获得无穷小电流偶极子。

接收器示例：半波长偶极子

我们将理想导体——半波长偶极子用作接收天线。

辐射入射到半波长偶极天线的动画演示。

许多文本探讨了无限细的导线，它的阻抗 \approx 73 \Omega，方向性为 D(\theta,\phi)\approx1.643\left[\frac{cos\left(\frac{\pi}{2}cos\theta\right)}{sin\theta}\right]^2。值得一提的是，这种天线的阻抗与具有半径的天线存在差异。我们讨论的接收天线的长度为 0.47 λ，长度与直径之比为 100。利用这些值，我们的模拟得到了 \approx 73 +3j \,\Omega 的阻抗，它接近于无限细导线的阻抗值，并且与实验值吻合良好。令人遗憾的是，对该数字进行比较没有理论价值，但是这强调了天线设计对数值模拟的需求。

下图比较了无限细偶极子与偶极天线仿真的方向性。因为天线是无损的，这相当于天线增益。您可以点击链接下载偶极天线模型。

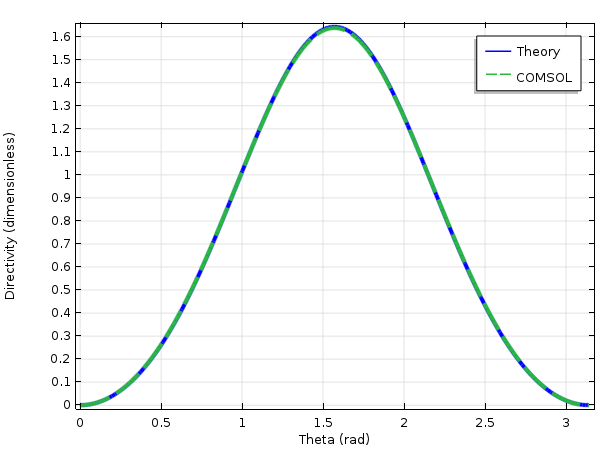
比较两个半波长天线（z 方向）的方向性与 θ 之间的函数关系。COMSOL Multiphysics® 仿真模型是一个具有很小半径的圆柱体，理论模型是一个无限细的天线。

计算接收功率

现在，我们可以使用弗里斯传输方程计算完美点偶极子发射的功率和半波长偶极子天线接收的功率。使用方程时，我们只需要了解增益和阻抗失配（或实际增益）、波长、天线之间的距离和输入功率。我们选择了使用电点偶极子，所以可以获得偶极矩，而不是输入功率和阻抗失配。要解决这个问题，我们可以去掉阻抗失配项，用完美电偶极子的辐射功率替代输入功率——实际上，输入功率等于辐射功率。

若假设发射器和检测器均位于 xy 平面，处于极化匹配状态，相隔 1000 λ，而且 \hat{z} 中发射极的偶极矩为 1 Am，则弗里斯方程关于接收功率的计算值为 380 μW。我们将在本系列的第 3 部分中模拟接收功率值，借此验证仿真技术，然后我们可以自信地从仿真中提取结果，并引入弗里斯方程无法解释的复杂性。

结语

在本篇博客中，我们介绍了多尺度模拟的概念，讨论了建模之前需要了解的相关术语、定义和理论。对于在电磁学和天线设计方面拥有深厚背景的专业人士而言，这或许是一篇快速回顾。如果您不熟悉本文介绍的概念，我们强烈建议您阅读一本介绍经典电磁学或天线理论的书籍。

在后续的博客文章中，我们将重点讨论如何在 COMSOL Multiphysics中实现多尺度模拟，并且会反复提及今天讨论的概念。

后续博客……

敬请期待多尺度模拟系列博客的更多文章：

• 在第 2 部分中，我们将使用电磁波，频域 接口模拟电点偶极子的发射过程，并讨论用于计算源的远场辐射的远场域 节点，演示如何将电磁波，频域 接口耦合到电磁波，光束包络 接口，借此模拟中间区的场。
• 在第 3 部分中，我们将模拟点偶极与相距任意距离的半波长偶极天线之间的辐射。为了验证模型，我们将计算半波长偶极天线接收的功率，并使用弗里斯传输方程验证结果。
• 在第 4 部分中，我们将使用几何光学 接口将发射源——点电偶极子耦合到射线光学仿真中。
• 在第 5 部分中，我们将使用几何光学 接口耦合两个天线，并再次验证结果，讨论这种更通用的方法如何用于不均匀的媒介和多路传输。