
当您在 COMSOL Multiphysics 中构建有限元模型时,都应该了解所使用的单元阶次。这对于多物理场模型尤其重要,因为对不同的物理场使用不同的单元阶次有一些明显的好处。今天,我们将复习单元阶次背后的关键概念,并讨论如何将它应用在一些常见的多物理场模型中。
什么是单元阶次?
每当解决有限元问题时,我们都会将真实解的场近似为域上的偏微分方程 (PDE)。 有限元法首先将建模域细分为更小、更简单的被称为单元 的域。这些单元由一组点定义,通常被称为节点,每个节点都有一组形函数 或基函数。每个形函数都与某些自由度 相关联。所有这些离散自由度的集合通常被称为解向量。
一旦计算出解向量,就利用解向量和所有单元中的所有基函数的集合,通过插值来构建求解域的有限元近似。单元阶次是指所使用的基函数的类型。
现在让我们将 COMSOL Multiphysics 中更常用单元的一些基函数可视化:二维拉格朗日单元。我们将看到一个方形域,由一个在每个角都有一个节点的单个四边形(四边)单元来划分网格。如果我们正在计算一个标量场,那么拉格朗日单元在每个节点上都有一个自由度。我们可以在下图中将一阶拉格朗日单元的形函数可视化。
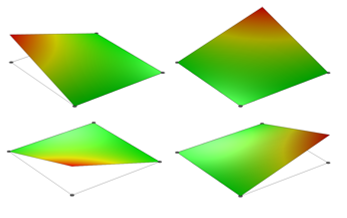
一阶正方四边形拉格朗日单元的形函数。
一阶形函数在一个节点上是统一的,在其他所有节点上都是零。这个单元上的完整有限元解是每个形函数乘以其相关自由度的总和。现在我们来比较一下一阶形函数和二阶形函数。
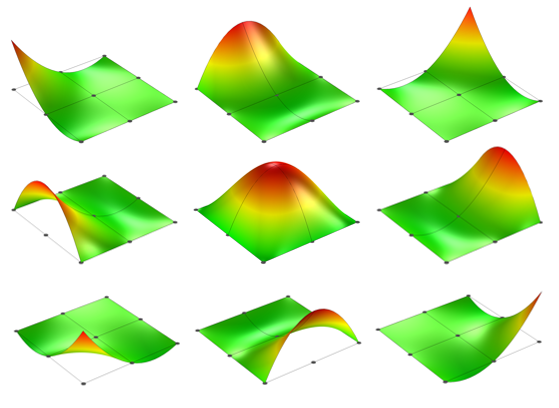
一个二阶方形四边形拉格朗日单元的形函数。
观察后发现,二阶四边形拉格朗日单元在边的中点和单元中心都有节点。它总共有9个形函数,同样,每个形函数在一个节点上是统一的,在其他地方是零。
现在,让我们来看看当我们的单个四边形单元表示的域不是完美的正方形而是具有一些弯曲边的域时会发生什么。在这种情况下,通常使用所谓的 等参单元,这意味着将使用与用于求解的同样的形函数来近似几何图形。对于一阶和二阶情况,该几何近似如下所示。
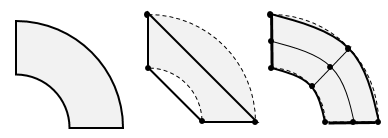
具有弯曲边的域。应用了单个一阶和二阶四边形单元。
正如我们在上图中所看到的,一阶单元只是简单地将曲边近似为直边。二阶单元更准确地逼近这些弯曲边界。这种差异被称为几何离散误差,我们在之前的博文中有更详细的讨论。等参一阶和二阶拉格朗日单元的形函数如下图所示。
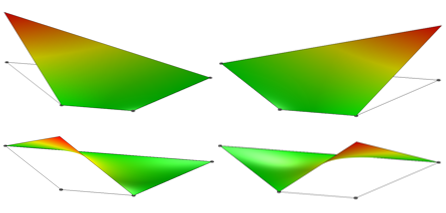
具有弯曲边的域的一阶等参拉格朗日单元的形函数。
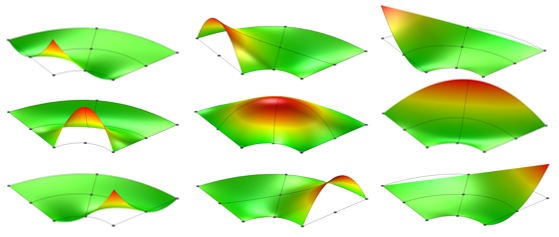
具有曲边域的单个二阶等参拉格朗日单元的形函数。
从以上两幅图中我们可以观察到,一阶单元将域的所有边近似为直线,而二阶单元更精确地近似曲线形状。因此,如果我们对具有弯曲边的域进行建模,我们需要沿着任意弯曲域边界使用多个线性单元,以便我们可以准确地表示域本身。
对于任何现实世界的有限元模型,当然总是会有多个单元描述几何形状。此外,请记住,无论单元阶次如何,我们都需要执行网格细化研究,也称为网格收敛研究。也就是说,我们将使用越来越细的网格(越来越小的单元)来解决相同的问题,并查看解是如何收敛的。在达到所需的精度后,我们可以终止这个网格细化过程。在椭圆薄膜的应力分析应用实例中,给出了网格细化研究的一个很好示例。
无论单元阶次如何,所有适定的单物理场有限元问题都将收敛于相同的答案。然而,不同的单元阶次会以不同的速率收敛,因此需要各种计算资源。下面,我们来探讨为什么不同的偏微分方程具有不同的单元阶次。
单物理场模型中的单元阶次
出于本次讨论的目的,我们仅考虑控制不随时间变化的常见单物理场问题的一组偏微分方程。我们可以将所有这些 偏微分方程 归入下面两大类之一:
- 泊松型:泊松型偏微分方程用于描述固体中的传热、固体力学、电流、静电学和静磁学、薄膜流动,以及受达西定律或理查兹方程支配的多孔介质中的流动。这些控制偏微分方程均采用以下形式:
- 传递型: 传递型偏微分方程用于描述流体和多孔介质中化学物质的传递和传热。这里的控制方程与泊松方程非常相似,只是多了一项——速度矢量:
\nabla \cdot ( -D \nabla u + \mathbf{v} u ) = f
额外的速度项产生的控制方程更接近于一阶偏微分方程。速度场通常通过求解 Navier-Stokes 方程来计算,这本身就是描述流体流动的一种输运方程。通常情况下,对于这样的问题,有一个较高的 Péclet 数或雷诺数。这就是为什么默认选择为这些偏微分方程使用一阶(线性)元素的原因之一。
请注意,对于雷诺数较低的流体流动问题,默认使用所谓的 P2 + P1 单元,通过二阶离散化求解流体速度并通过一阶离散化求解压力。P2 + P1 单元是蠕变流、Brinkman 方程 和自由和多孔介质流动 接口的默认值。对于两相流,水平集和两相流,相场 接口也是如此。此外,任何类型的传输或流体流动接口都使用稳定性来更快、更稳健地解决问题。有关稳定方法的概述,请查看我们之前的博客文章理解稳定方法。
注意,这是一个二阶偏微分方程,因此二阶(二次)单元是 COMSOL Multiphysics 中所有这些类型方程的默认选择。
那么,我们如何检查特定物理接口使用的单元阶次的默认设置呢?在模型开发器中,我们首先需要显示菜单并切换离散化。这样做之后,会看到物理场接口设置中的离散化部分,如下面的截图所示。
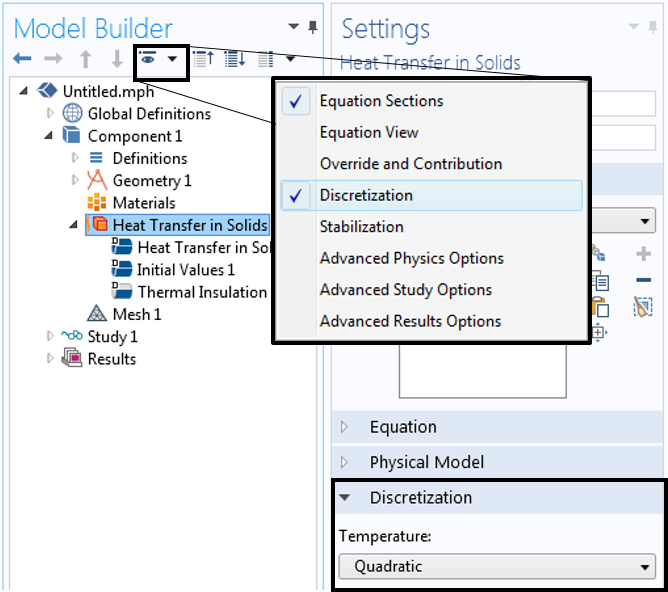
显示如何查看物理场接口的单元阶次的屏幕截图。
请记住,如果仅使用单个物理场,我们只要记得执行网格收敛研究,使用哪种单元阶次通常并不重要。具有不同单元阶次的解可能需要差异相当大的内存和时间来求解,但它们都会通过足够的网格细化收敛到相同的解。然而,当我们开始处理多物理场问题时,事情会变得有点复杂。接下来,我们将看看多物理场建模的两个特殊情况,在这些情况下,我们应该了解单元阶次。
共轭传热:固体中的传热与流体中的传热
COMSOL Multiphysics 包括传热和流体流动之间预定义的多物理耦合,旨在模拟被周围流体冷却或加热的物体的温度。对于层流和湍流流体,传热模块和 CFD 模块提供了共轭传热界面(以及功能等效的非等温流动界面)。
COMSOL Multiphysics 在传热和流体流动之间包含一个预定义的多物理场耦合,用于模拟被周围流体冷却或加热的物体的温度。对于层流和湍流的流体流动,可以使用传热模块和CFD 模块中的共轭传热 接口(和功能上等同的非等温流 接口)。
共轭传热接口由传热接口和流体流动接口两个物理场接口组成。流体流动接口(无论是层流还是湍流)采用线性单元阶次求解流体速度场和压力场。传热接口既可以求解流体中的温度场,也可以求解固体中的温度场。在整个温度场中,无论是固体域还是流体域,都使用相同的线性单元离散。
现在,如果我们通过手动添加各种物理场接口来设置共轭传热问题,则需要小心。如果从固体传热 接口开始,并在该接口中添加流体传热 域特征,则默认情况下温度场将使用二阶离散化。通常不建议这样做,因为它需要比一阶温度离散化更多的内存。流体流场的默认一阶离散化证明在整个模型中使用一阶单元是合理的。
还值得一提的是相关的多物理场耦合:传热模块提供的局部热非平衡 接口。该接口旨在求解流经多孔介质的流体的温度场以及流体流经的基质的温度。也就是说,空间中的每个点都有两种不同的温度,即流体温度和固体基质温度。该接口对两个温度同样使用了一阶离散化。
结束语
我们已经讨论了在COMSOL Multiphysics中离散化阶次的含义,以及为什么它与经常出现的两种不同的多物理场情况相关。如果您正在组合自己的多物理场模型,那么就需要记住单元的阶次。
此外,如果您构建的多物理场模型的单元阶次与我们在这里概述的不一致,那么最好解决可能发生的情况。事实证明,在许多情况下,最糟糕的情况是您的模型只需要更多的内存,并且收敛到解的速度会更慢。在网格细化的限制下,不同物理场中单元阶次的任何组合都将得到相同的结果,但收敛速度可能非常缓慢和振荡。如果您观察到解的任何空间振荡(例如,应力场看起来像波纹或波浪),那就应该检查单元阶次。
今天的博文是为 COMSOL multiphysics 中的单元选择问题而设计的实用指南。在 Robert D. Cook, David S. Malkus, Michael E. Plesha, Robert J. Witt 等人的著作 Concepts and Applications of Finite Element Analysis 一书中,对混合(混合)有限元方法的稳定性判据有更深入的讨论,有兴趣的同学可以深入研究。



评论 (2)
雄 纪
2021-11-18整篇没有讲到三次单元,而案例库中光学模块无缘无故使用了三次拉格朗日单元
Min Yuan
2021-11-19 COMSOL 员工您好,因为在射线光学模块中对壁面的精度要求比较高,所以更改单元阶次,使用三阶拉格朗日单元以得到精确解。本篇博客中通过对弯曲边的域进行建模来比较一阶形函数和二阶形函数,得到高阶形函数会更准确逼近弯曲边的域,同时会需要更多计算资源的结果。可以参考以下对理解和改变单元阶次的相关描述https://cn.comsol.com/support/knowledgebase/1270