
在上一篇博客中,我们介绍了线性静态问题的网格划分注意事项。其中,网格收敛是一个关键概念,因为随着网格的细化,解将变得更加精确。这篇博客,我们将更加深入地探究:对于线性静态有限元问题,如何选择合适的网格进行网格收敛研究。
不同的单元类型
在之前的博客中,我们介绍了 4 种不同的三维单元类型:四面体、六面体、棱柱和金字塔形:

这 4 种单元可以进行各种组合,对任何三维模型进行网格剖分。(对于二维模型,可以选择三角形和四边形单元。因为它只是三维的一个逻辑子集,不需要太多额外的解释,所以我们这里将不会进行过多介绍。)为什么要使用不同的单元,我们在上一篇文章中没有深入介绍。
不同单元类型的适用情形
对于 COMSOL Multiphysics 中的大部分物理场而言,四面体单元是默认的单元类型。四面体也称单纯形网格,简单讲就是,可以使用四面体单元对 任何 三维体进行网格划分,无论什么形状或拓扑结构。它们也是唯一一种可用于自适应网格细化的单元类型。因此,四面体单元通常是首要选择。
另外三种单元类型(六面体、棱柱和金字塔形)仅用于确实需要时。首先应该注意的是,这些单元并非总能划分具体几何。根据划分的算法,通常需要进行更多的用户输入来创建这类网格,因此在进行网格划分前,应该首先问一下自己为什么要这样划分。这里,我们将介绍使用六面体和棱柱单元的原因。金字塔形仅在需要在六面体和四面体网格之间创建一个过渡区域时使用。
在此,我们有必要介绍一些背景信息。在第一台电子计算机诞生之前,有限元方法背后的数学理论就已经得到了充分的发展。第一台运行有限元程序的计算机中布满了真空管和手工制作的电路,虽然后来的晶体管极大地改进了计算机,但 25 年前发明的超级计算机的时钟速度也不过与如今流行的一些配件(谷歌眼镜)相同。
最早求解的一些有限元问题在结构力学领域,早期程序主要是为一些内存极小的计算机编写的。因此,会使用一阶单元(通常使用特定的积分方案)来节省内存与时间。但在结构力学问题中,使用一阶四面体单元会带来严重的问题,而使用一阶六面体单元则可以得到精确的结果。
由于这些较早期的代码产物,现在,许多结构工程师仍然更喜欢使用六面体而非四面体单元。
事实上,在 COMSOL 中使用二阶四面体单元求解结构力学问题会得到精确的结果,与使用六面体单元的差别仅在于内存需求和求解时间。
在 COMSOL 中使用六面体和棱柱单元的主要是因为它们可以极大地降低网格中的单元数。这些单元可能有极高的长宽比(最长边与最短边的比例),而用于创建四面体网格的算法则会尽量保持长宽比接近一致。当您知道解在特定方向上会逐渐变化,或者您对这些区域中的精确解并不感兴趣,因为您知道感兴趣的结果在模型的其他位置时,使用具有高长宽比的六面体和棱柱单元较为合理。
示例 1:轮毂
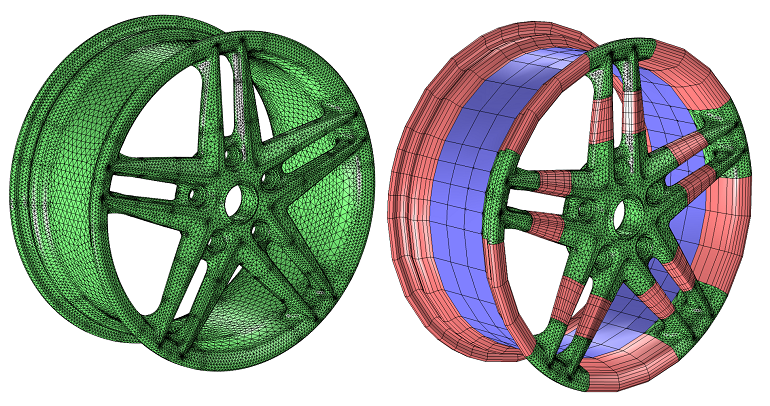
考虑一个轮毂示例,如下所示。
左边轮毂中的网格仅由四面体构成,而右边轮毂中的网格则包括四面体(绿色)、六面体(蓝色)、棱柱(粉色),以及位于这些网格过渡区的金字塔形网格。在孔和拐角处这些我们预期应力会更高的区域,混合网格使用了较小的四面体单元。辐条和轮毂附近使用了六面体和棱柱单元。峰值应力不会出现在轮毂或辐条处(至少在静载荷下),我们可以有把握地假定这些区域应力的变化相对较慢。四面体网格包含大约 145000 个单元和 730000 个自由度。混合网格包含接近 78000 个单元和大约 414000 个自由度,求解时间与内存使用都大约为原来的一半。混合网格需要大量的用户设定,而四面体网格基本上不需要用户设置。
注意:自由度和求解问题所需内存之间并没有直接的联系。这是因为不同单元类型的计算要求不同。二阶四面体中每个单元有 10 个节点,而二阶六面体则有 27 个。这说明使用六面体单元时,单个网格矩阵更大,对应的系统矩阵也更密集。求解所需的内存(和时间)与要求解的自由度数、节点间的平均连通性,以及其他一些因素有关。
示例 2:负载弹簧
另一个示例是对负载弹簧的结构分析,如下图所示。由于沿弹簧螺旋长度方向的变形几乎一致,因此采用一个能描述整体形状和截面,并且沿螺旋长度方向相对较延伸的网格单元是合理的。使用棱柱进行网格划分需要 504 个单元和 9526 个自由度,四面体单元则需要 3652 个单元和 23434 个自由度。因此,尽管单元数量相差很大,但自由度数差别不大。

示例 3:晶圆上的材料
使用六面体和棱柱单元的另外一个重要原因是,几何在一个方向上包含极薄的结构,例如晶圆上的外延材料层,冲压钣金件或夹层式复合材料。
下图所示为刻蚀在基底上的一层非常薄的轨迹材料。使用四面体单元对薄层进行划分,网格将被划分成非常小的单元,但如果使用棱柱单元划分,该区域的网格将被划分成非常薄的单元。只要几何结构中包含比零件中最大尺寸小 10-3 倍或更小的层,就应该使用六面体和棱柱单元进行网格划分。
更多示例
此外,COMSOL 还提供了多种边界条件,可用于代替模拟薄层材料。例如在下列 4 个电磁仿真案例中,考虑了具有相对较高和较低电导率,以及相对较高和较低磁导率的薄层材料。
COMSOL 的大部分物理场接口中都包括类似的边界条件。使用这类边界条件可以避免对这些薄层进行完整网格划分的需求。
最后,上述讨论仅适用于线性静态有限元问题。对于非线性静态问题、时域或频率问题,应使用不同的网格划分方法。
结束语
总之,在开始对线性静态问题进行网格划分之前,应牢记以下注意事项:
- 如果可能,请使用四面体网格;它们对用户交互的要求最低,并支持自适应网格细化
- 如果你预先知道解在一个或多个方向上变化缓慢,那么应该在这些区域使用含较高长宽比的六面体或棱柱单元网格
- 如果几何包括薄层材料,应该使用六面体或棱柱,或考虑使用边界条件来代替
- 始终进行网格细化研究,并在细化网格时随时监控内存要求以及解的收敛







评论 (7)
刘 阳
2016-05-18请问博客里对应的案例能给出嘛
鹏 刘
2018-04-09请问薄膜材料需要如何进行六面体和棱柱网格划分?
宇航 秦
2018-04-13刘阳,您好!
有关模型的问题请发送至 support@comsol.com
谢谢。
宇航 秦
2018-04-13刘鹏,您好!
有关模型的问题请发送至 support@comsol.com
谢谢。
彦松 陈
2019-06-13请问是否可以几何建模并提取不同网格单元对应的单元矩阵?
毫 刘
2019-06-19请问博客里对应的案例能给出嘛
神昌 曾
2020-01-16“自由度和求解问题所用内存之间并没有直接联系。这是因为不同单元类型的计算要求不同。二阶四面体中每个单元包括 10 个节点,而二阶六面体则是 27 个。这意味着使用六面体网格时,单个网格矩阵更大,对应的系统矩阵会更密集。求解所需的内存(和时间)依赖于要求解的自由度数、节点间的平均连通性,以及其他一些因素。”
上面这个描述有点误导人,虽然二阶四面体10个节点,二阶六面体是20个(不是上面说的27个),但一个六面体占用的空间需要5-6个四面体来填充。说单个网格六面体比四面体矩阵更大没有意义。