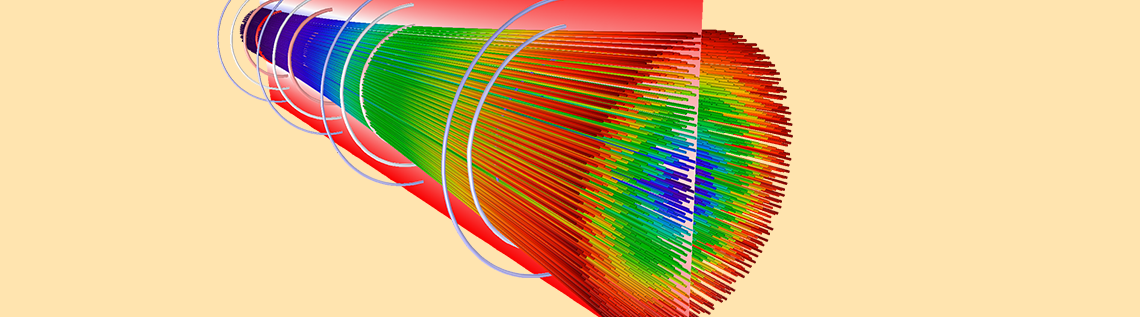
电子枪常用于阴极射线管、电子显微镜、光谱仪和粒子加速器中,其工作原理是从热阴极或等离子体中提取电子,然后将其加速到高动能。设计制造电子枪的一个主要挑战是电子互相排斥,因此电子束容易散开。今天,我们将讨论如何对一种最早设计用来抵消这种静电斥力的电极配置进行模拟——皮尔斯电子枪。
电子枪设计
一个好的电子枪设计必须能够做到以下几点:
- 提取足够多的电子,即获得足够的电子束流
- 将电子加速到一定的动能
- 将光束聚焦在特定位置
通常,当电子从阴极或等离子体源发射出来时,速度相当慢,然后它们会被外部场加速。一种非常简单的加速方法是使电子束通过一个固定电势的金属栅极。
两个带电粒子之间的力
所有发射的电子束之间都会产生相互斥力。考虑在位置 r 1 和 r 2 处的两个带电粒子,其电荷分别为 q1 和 q2。根据库仑定律,可以计算粒子 2 施加在粒子 1 上的力,
{4\pi\epsilon_0}\frac{\mathbf{r}_1-\mathbf{r}_2}{\left|\mathbf{r}_1-\mathbf{r}_2\right|^3}
其中,ε0=8.854187817×10-12F/m 是一个被称为真空介电常数的物理常数。
如果 q1 和 q2 具有相同的符号(即,两个粒子都带正电或负电),则粒子 1 上的力指向粒子2的反方向。如果一个粒子带正电而另一个粒子带负电,则粒子1上的力将指向粒子2。因此,同性电荷相斥,异性电荷相吸。
随着粒子彼此靠近,吸引力或斥力会变得更强。如果将两个电子之间的距离缩小一倍,它们彼此施加的斥力将增加四倍。
大量带电粒子之间的力
大多数现实世界的系统都包含大量的电子,而不仅仅是两个。作用在电子上的总库仑力是所有其他粒子施加的力之和。例如,作用在第一个粒子上的总力为
其中,N 是电子总数。
想象一个包含许多电子的圆柱形电子束。对于靠近电子束中心的电子,在任一侧上都有相同数量的其他电子,因此,如果我们取作用于该电子的力的矢量和,则库仑力将大部分被抵消。另一方面,对于靠近电子束边缘的电子,净力会将其推向离中心更远的地方。因此,如果束流电子最初是彼此平行移动的,则随着电子束传播,它们将开始扩散或发散。
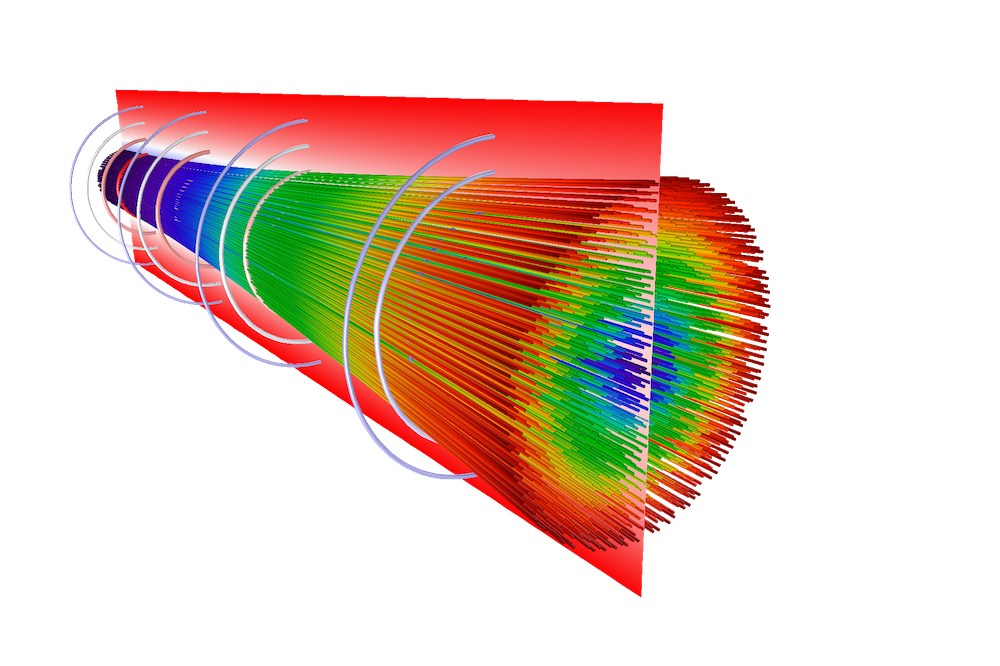
发散的电子束。电子束在电子速度平行的束腰(左)被释放。在右侧,电子向四面八方扩散。
查看演示电子束如何在自由空间中发散的示例,请参阅 COMSOL 教程模型自然电位引起的电子束发散和相对论发散电子束引起的电子束发散。
导致电子束扩散的斥力在束流电子最慢的的地方最强,因为这些区域通常具有最高的电荷密度。因此,设计电子枪时的关键技术挑战之一通常是在束流电子发射之后立即将电子束聚焦在第一加速间隙中(参考文献1)。
寻找最佳电极形状
我们的目标是设计一种电子枪几何形状,以使电极的形状抵消电子束之间的库仑斥力,从而使电子束沿直线传播而不会扩散。
首先,考虑在平面外(z)方向上的二维薄电子束是均匀的。电子束将沿正 y 方向传播。束流电子首先从位于 y=0 的阴极(V=0)发射出来,并被吸引到位于某个高度 y=d 的阳极(V=V a)。
让我们从一个简单的解开始,其中电子束在x方向上无限宽。在这种情况下,任何电子束都可以被认为是在电子束的中心,左右两侧的电力会相互抵消。
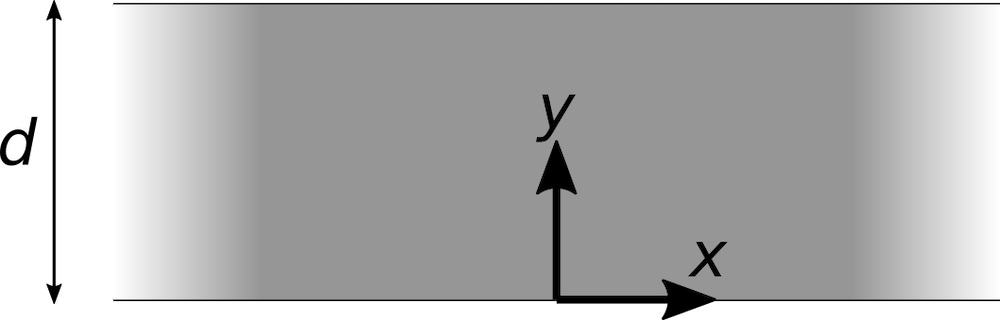
在两个扁平电极之间的简单薄电子束,在 +x 和 – x 方向上无限延伸。
在不导致电子向后排斥的情况下,理论上可以从阴极提取的电流存在一个最大值。这就是所谓的空间电荷极限,而在此电流下释放电子的阴极就是空间电荷极限。在两个平行电极之间进行空间电荷极限发射期间,间隙中的电势遵循 Child 定律(参考文献2)给出的分布,
{d}\right)^{4/3}
现在假设电子仅在 x < 0 区域中流动,并且 x > 0 区域中没有电荷。
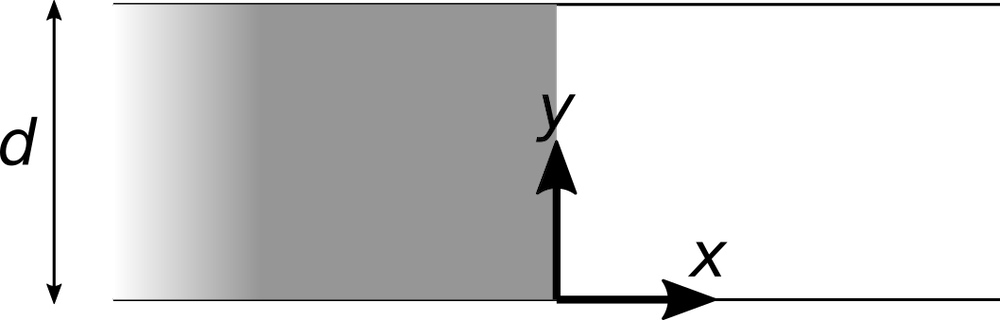
如果电极保持其扁平形状,则由于电子束中的静电排斥作用,一些靠近 y 轴的电子将溢出到 x > 0 的区域中。
因此,因为电子束边缘附近的电子感觉到来自其他电子的库仑力不平衡,所以当电子束具有有限的尺寸时,会发生电子束的发散或扩散。在下一节中,我们将介绍一种分析方法来更改电极的形状,以使电子束直接朝上,并且没有电子溢出到 x > 0 的区域中。
电子枪设计的皮尔斯方法
假设阴极和阳极在 x < 0 区域中仍然是扁平的,但是现在它们在 x > 0 区域中呈现不同的形状。这些电极形状的确切功能形式尚不清楚。
因为在x > 0的区域中没有电荷,所以电势必须满足拉普拉斯方程,
考虑复数u=y+ix。皮尔斯的方法(参考资料 1、3)首先观察到 u 的任何二次微分函数(称为 f(u))也将满足拉普拉斯方程。这可以通过反复应用链式法则来证明,
\frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2}
&= \frac{\partial}{\partial x}\left(\frac{\partial u}{\partial x}\frac{\partial f}{\partial u}\right)
+\frac{\partial}{\partial y}\left(\frac{\partial u}{\partial y}\frac{\partial f}{\partial u}\right)\\
&= \frac{\partial}{\partial x}\left(i\frac{\partial f}{\partial u}\right)
+\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial u}\right)\\
&= \frac{\partial u}{\partial x}\frac{\partial}{\partial u}\left(i\frac{\partial f}{\partial u}\right)
+\frac{\partial u}{\partial y}\frac{\partial}{\partial u}\left(\frac{\partial f}{\partial u}\right)\\
&= i^2\frac{\partial^2 f}{\partial u^2} + \frac{\partial^2 f}{\partial u^2}\\
&= -\frac{\partial^2 f}{\partial u^2} + \frac{\partial^2 f}{\partial u^2}\\
&= 0
\end{align}
考虑到这一点,将 x > 0 区域中的电势定义为 f 的实部,
然后,V 在该无电荷区域也将满足拉普拉斯方程。为了确保电势在 x=0 处连续,V 必须满足 Child 定律(参考文献2)给出的电势分布,
\right)^{4/3}\right]
阴极只是在复平面中满足 V=0 方程的一组坐标。类似地,阳极是在复平面中满足 V=Va 方程的一组坐标。
在这一点上,用圆柱形电极坐标重写 u 很方便,
注意上式中,θ=0 是正 y 方向而不是 x 方向。现在,我们对于 x > 0 区域中的电势的表达式为
{d}e^{i\theta}\right)^{4/3}\right]
由于 r 和 d 是实数,因此可以简化为
然后调用欧拉公式得出最终结果
\right)^{4/3}\cos\frac{4\theta}
{3}
现在,阴极和阳极的形状就是刚插入最后一个表达式时分别给出 V=0 和 V=Va 的曲线。
V=0 的解是直线
= \frac{\pi}{2}
或与电子束传播方向成 67.5° 角。
V = Va的解是曲线,
因此,皮尔斯枪的设计算法预测,使用与电子束传播方向成 67.5° 角的直阴极和弯曲阳极,可以使电子束完全保持直线。
创建 COMSOL Multiphysics® 几何
在上一节中发现的阳极曲线渐近地接近阴极线,但从未完全与阴极线相吻合。完美的皮尔斯电子枪在正 x 方向无限延伸,因此我们必须在某个点任意切断它。
在下图中,直线是阴极,而其上方的长曲线是阳极。这两条线可以无限远地延伸,但永远不会相遇。因此,对于更实用的模型,我们绘制了一条与阴极和阳极都相交的线,然后使用 COMSOL Multiphysics® 中的转换为实体操作来形成由这些曲线所界定的区域。相交线段垂直于阴极绘制,因为我们希望电场指向该方向。
左侧的实心矩形是电子束传播区域,直线 x=0 是这里的一条对称轴。因此,整个皮尔斯枪的几何形状在电子束的两边都具有相同的弯曲阳极形状。
在截断阴极和阳极曲线之前的皮尔斯电子枪的几何形状。
对粒子场相互作用进行建模
在此模型中,我们使用专用的空间电荷受限发射多物理场耦合节点在正 y 方向释放空间电荷受限的电子束。然后,为了考虑束流电子之间的相互静电斥力的影响,我们使用了专用的电-粒子场相互作用多物理场耦合。这导致束流电子对域中的空间电荷密度做出贡献,然后在求解电势时将其包括在静电接口中。
然后,获得用于电势和粒子轨迹的自洽解的最终算法如下:
- 跟踪粒子,而无需考虑束流电子之间的静电排斥。根据此解,估算电子束中的空间电荷密度。
- 使用估计的空间电荷密度以及阴极和阳极表面的边界条件,计算出静态电势。
- 使用上一步中的电势来定义粒子上的电力。再次跟踪粒子,并计算电子束中的空间电荷密度。
- 继续在步骤 2 和 3 之间交替进行固定次数的迭代,或者直到解在迭代之间没有明显变化为止。
结果
镜像 数据集用于反映y轴上的电势分布。下图显示了根据其速度着色的粒子轨迹,其中绿色是最快的。域中的空间电荷密度以灰度绘制,阴影越深表示空间电荷密度越大。显然,电荷密度在靠近阴极的狭窄区域中最大,并且随着粒子加速而减小。
皮尔斯枪中的电势分布和粒子轨迹。
以下动画显示了粒子在接近阳极时如何加速。在这里,灰度背景显示了一些等电位轮廓。电子束区域中的粒子沿直线移动,并且电子束横截面中的等电位轮廓是水平的,这都很好地表明倾斜的阴极和弯曲的阳极正确地平衡了电子束中的静电斥力。
自己尝试
请单击下面的按钮,下载皮尔斯电子枪模型。
延伸阅读
在另一个模型Child 定律基准指南中,提供了有关 Child 定律及其推导的一些有用的理论细节。
Child 定律是基于一个简化的近似,它忽略了释放电子的热速度。实际上,室温下的粒子离开阴极后,可以以每秒几百米的速度四处飞行。要了解有关发射电子的热分布及其对空间电荷受限电子发射(有时称为 Langmuir-Fry 模型(参考文献4,5))的影响的更多信息,请参见平面二极管中的热电子发射示例。
参考文献
- S. Humphries, Stanley,Charged Particle Beams, Dover, 2013.
- J.R. Pierce, Rectilinear electron flow in beams, Journal of Applied Physics, vol. 11, no. 8 pp. 548–554, 1940.
- C.D. Child, “Discharge from hot CaO”, Physical Review (Series I), vol. 32, no. 5, pp. 492–511, 1911.
- T.C. Fry, “The thermionic current between parallel plane electrodes; velocities of emission distributed according to Maxwell’s law”, Physical Review, vol. 17, no. 4, pp. 441–452, 1921.
- I. Langmuir,“The effect of space charge and initial velocities on the potential distribution and thermionic current between parallel plane electrodes”,Physical Review, vol. 21, no. 4,pp. 419–435, 1923.,



评论 (0)