在之前博客中,我们了解了为什么表面是具有特殊化学意义的场所,并讨论了用于描述表面反应的理论,包括在多孔介质均质模型中描述表面。本文,我们将讨论化学物质通过 吸附 吸作用附着到表面时的行为。吸附作用在许多催化和检测过程中发挥着重要作用,因此文中也会考虑如何在模型中表征化学吸附作用。
什么是吸附?
有时候,化学物质会吸附在表面,这种现象可能发生在气相中的固体表面以及浸没在液体溶液中的固体表面。将化学物质聚集在表面的能力对检测和分离过程都非常重要,这也是催化反应的一种方式。在此系列博客的第一篇文章中,我们讨论了为什么表面通常具有独特的化学性质。
黏附在表面的过程称为吸附。注意,请不要将吸附与 吸收 混淆,吸收是指化学物质被吸收到固体或溶液本体中。
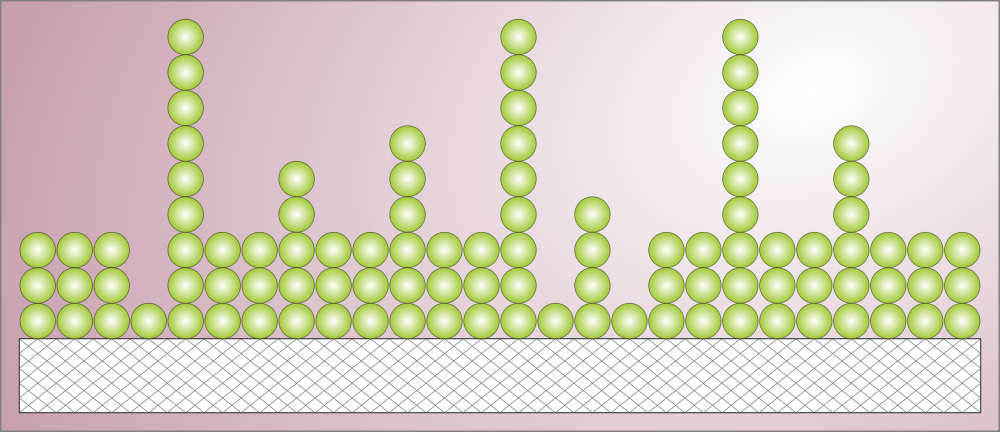
BET 多分子层吸附(吸附的一种类型)示意图。图片由 Life of Riley 提供。获 CC BY-SA 3.0许可,通过 Wikimedia Commons 共享。
吸附可以是表面与吸附物之间直接形成化学键 (化学吸附) ,也可以是表面与吸附物之间通过氢键或范德华力等分子间作用力产生的吸引(物理吸附 )。一般来说,通过物理吸附的分子在表面上更容易迁移,吸附力较弱。
等温吸附
吸附过程可以描述为一种平衡反应:
{\smash
{\leftarrow}
\vphantom{_{\vbox to.5ex{\vss}}}}$}} A(ads)
式中,气相中的化学物质 A(g) 称为吸附物:它以一定的吸附率吸附,并以一定的解吸速率解吸。
如何从数学角度描述这个平衡反应呢?美国物理化学家 Irving Langmuir 提出了一种最简单的方法。他在模型中提出了以下假设:
- 吸附物存在最大表面浓度 csat(mol m-2),在该浓度下表面趋于饱和
- 吸附速率常数与吸附物的表面覆盖率无关:也就是说,所有吸附位点都相同且相互独立
- 吸附是二级反应过程,其速率与表面相邻本体相中的吸附物浓度,以及空位的比例成线性关系
- 解吸是一级反应过程,其速率与吸附物的表面覆盖率呈线性关系
基于这些假设,吸附到表面的物质通量可以描述为:
{ads} = k_\mathrm{ads}
\,c_\mathrm
{A} c_\mathrm{sat} (1-\theta)
式中 Nads 是表面物质通量 (mol m2 s-1) ;kads 是吸附速率常数 (m3 mol-1 s-1);cA 是与本体相邻的表面浓度 (mol m-3);θ= cA,ads/csat (无单位)是吸附物的表面覆盖率,因此(1-θ)是空位的比例。
同样,由于解吸作用而脱离表面的物质通量可以描述为:
式中,kdes是解吸速率常数 (s-1)。
在平衡状态下,吸附物的表面覆盖率是恒定的,因此表面的吸附量和脱附通量必须相等。使上述表达式相等并消去同类项,可以得到:
(1-\theta) = \,\theta
吸附速率常数与解吸速率常数之比 (kads/kdes) 是吸附平衡常数,通常用大写字母 Kads 表示。平衡常数越大,吸附的热力学驱动力就越大。重新排列上述表达式,吸附物的表面覆盖率可以表示为
{ads} c_\mathrm{A}}{1+K_\mathrm{ads}
c_\mathrm{A}}
这就是 Langmuir 等温吸附公式。在给定温度条件下,当 Kads 取某一特定值时,就能够预测平衡状态下吸附物的表面覆盖率随其本体浓度的变化情况。
当然,Langmuir 的模型是一个简单的近似。在真实的吸附系统中,相邻吸附分子之间一般都存在相互作用,所以随着表面覆盖率的增加,吸收额外的物质会变得更加容易或更加困难。为此,研究人员通过开发更复杂的数学模型来更精确地反映真实的吸附系统。其中, Freundlich 等温吸附 模型包含一个额外的经验常数,可以考虑吸附分子之间的相互作用。BET 等温吸附 模型可用于发生多层吸附的系统,即第二层和后续各层吸附分子与相同类型的分子结合,而不是与基底的底层表面结合。
在 COMSOL Multiphysics® 软件中定义吸附
在使用 COMSOL Multiphysics® 软件建立化学物质传递和反应模型时,可以通过多种方法在模型中表征吸附作用。
对于均质多孔介质中的吸附,可以通过 多孔介质传递属性 和 部分饱和多孔介质 域特征中特殊的 吸附子节点来表征 。在这个子节点中,用户可以为任意本体物质定义 “Langmuir”、“Freundlich” 或“用户定义”吸附。这里,假设吸附物质与本体物质处于热力学平衡状态,因此等温吸附关系完全成立。有关如何使用 吸附 子节点的示例,请参见下图设置:
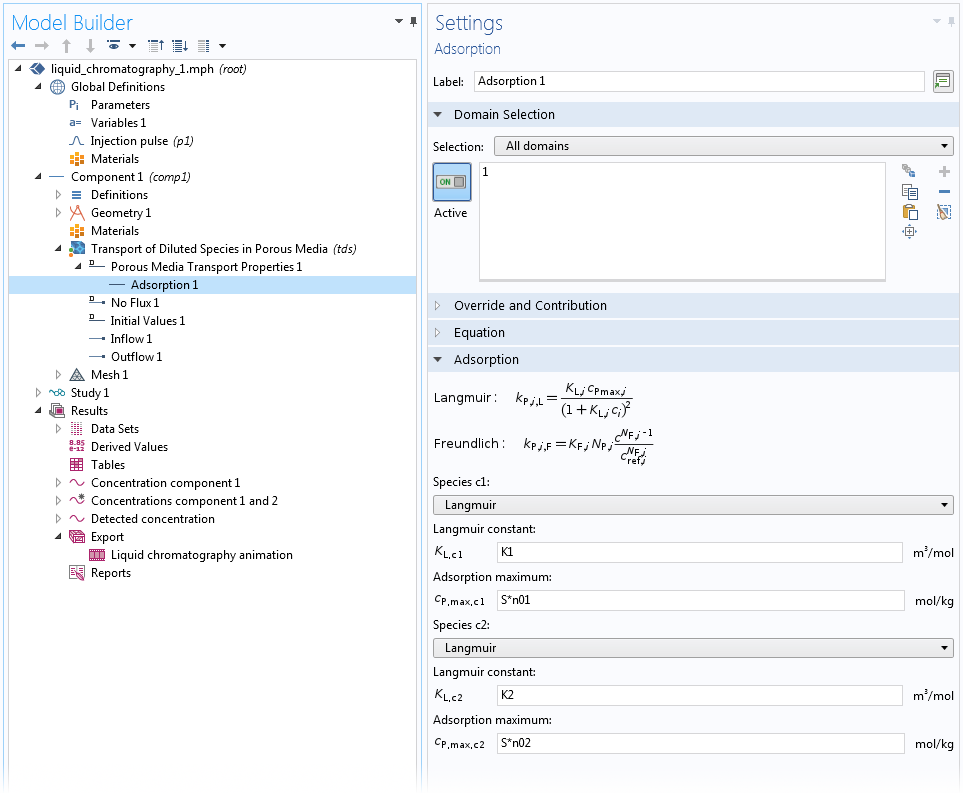
在高效液相色谱(HPLC)系统模型中,使用 Langmuir 等温吸附模型设置两种物质在均匀介质上的吸附过程。
如果吸附或解吸过程受动力学控制,有限速率常数就变得非常重要,并且表面不再处于平衡状态,设置中就会涉及更多细节。这时,需要使用另一个接口来描述吸附物质的表面浓度。例如本系列文章第一篇中所讨论的,可以使用 表面反应 接口来描述吸附物质。或者,如果描述通过多孔介质中的表面分布,可以使用 稀物质传递 接口,并将扩散系数和对流速率场设置为零。
吸附过程描述的是从本体(气体或液体)相迁移到表面的物质通量。通过在边界添加这种 通量 或在均质域中添加 反应,就可以描述上述吸附反应。对于此反应的动力学和热力学描述,可以选择遵循 Langmuir 等温吸附或者更复杂的反应机理,包括用户定义的任意形式的动力学表达式。请注意,直接在物质名称后面键入 (ads) 也可以将吸附物质添加到 反应工程 或 化学 接口中定义的反应机理(控制方程)中。
使用自定义的化学反应方程来表征吸附的另一个原因是竞争性吸附,当存在竞争性吸附现象时,两种或多种吸附物质会共享同一吸附位点。这种现象是 催化剂中毒 的常见原因:由于另一种分子吸附力较强,催化剂无法吸附预期的物质。这可能导致反应所需的催化剂永久失活。
涉及吸附的案例模型
COMSOL Multiphysics 案例库中内置了很多案例模型,演示了不同类型的吸附。
液相色谱法
高效液相色谱(HPLC)吸附系统使用一维模拟,即在色谱柱流动相的流动方向上建立一维模型。这里,两种组分不同的吸附平衡是由于使用了不同的 Langmuir 平衡常数定义,导致两种组份的停留时间不同。在稳定的溶剂流动与不同吸附速率的共同作用下,不同的吸附组分在空间和时间上得以分离。
模拟中,结合使用 多孔介质中的稀物质传递 接口与 吸附 子节点来表示平衡吸附过程。
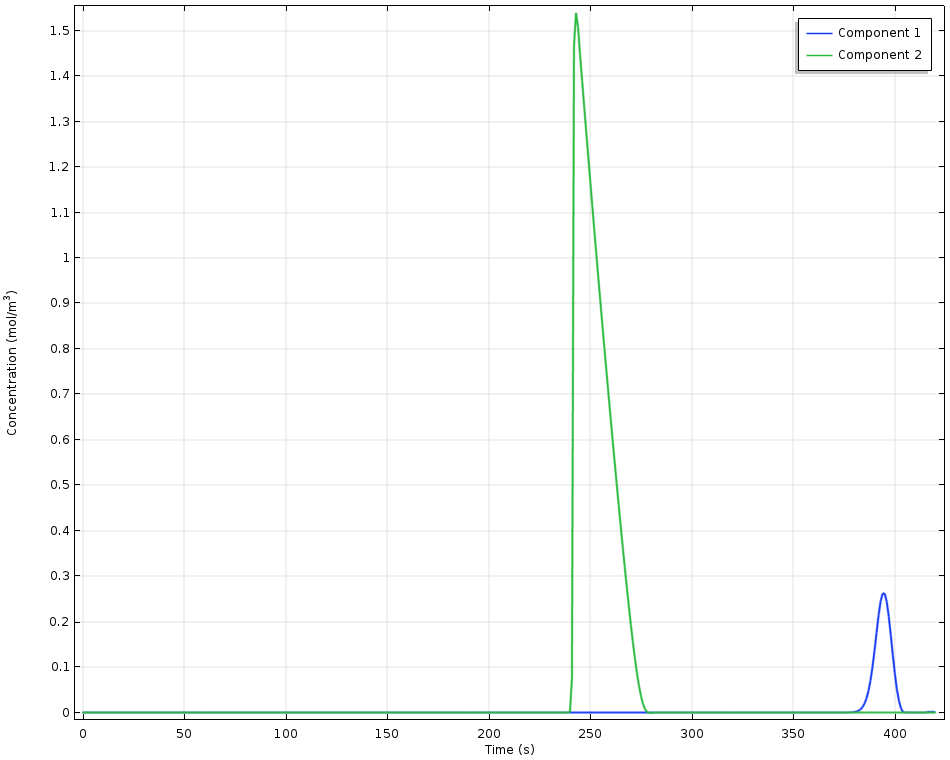
高效液相色谱实验中检测到的浓度与时间的关系。组分 1 具有较高的吸附能力,因此停留时间更长。
蛋白质吸附
在上一篇关于蛋白质吸附过程的博客中,我们讨论了在离子交换柱内,蛋白质通过与柱表面的特定位点结合吸附并置换离子。对于存在多种蛋白质相互作用的更复杂的反应体系,可以使用 化学 接口描述,然后再与 稀物质传递接口(描述溶液中可迁移的物质)和 表面反应 接口(描述被吸附的物质)耦合模拟。
离子交换柱中的蛋白质吸附。
传递和吸附
在这个示例中,溶液中某物质的扩散和对流是通过 稀物质传递 接口描述的。化学物质也会在某个边界上的位点上吸附,这里通过 一般形式边界偏微分方程 输入用户自定义方程来表征表面覆盖率。如上所述,该动力学方程基于吸附和解吸速率的 Langmuir 近似方程,但没有假设反应达到平衡。因此,Langmuir 等温吸附本身不一定成立,而吸附和解吸通量则需要动态考虑。
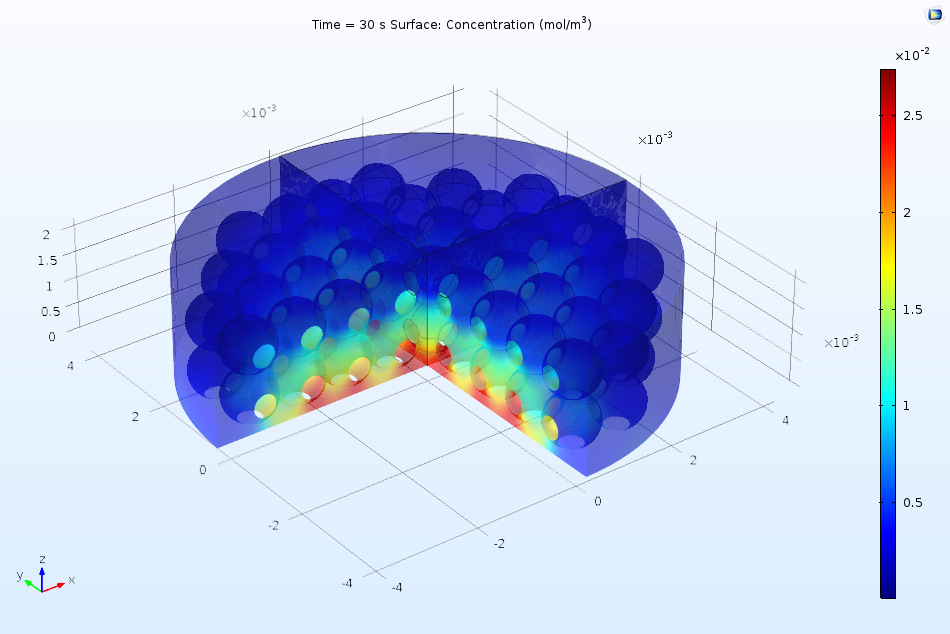
下图显示了溶解的吸附物如何流过活性表面,并使吸附的表面浓度随着时间的推移而逐渐增加。由于浓度在 2 s 后仍在继续上升,但很明显还没有达到平衡,因此选择动力学模型(而不是热力学模型)描述这一表面吸附过程是合适的。一般来说,上游(左边)的表面覆盖率较高,这是因为上游溶液中的浓度较高,已经发生少量吸附。而在下游边缘,表面浓度升高是由于扩散引起的边缘效应所致。
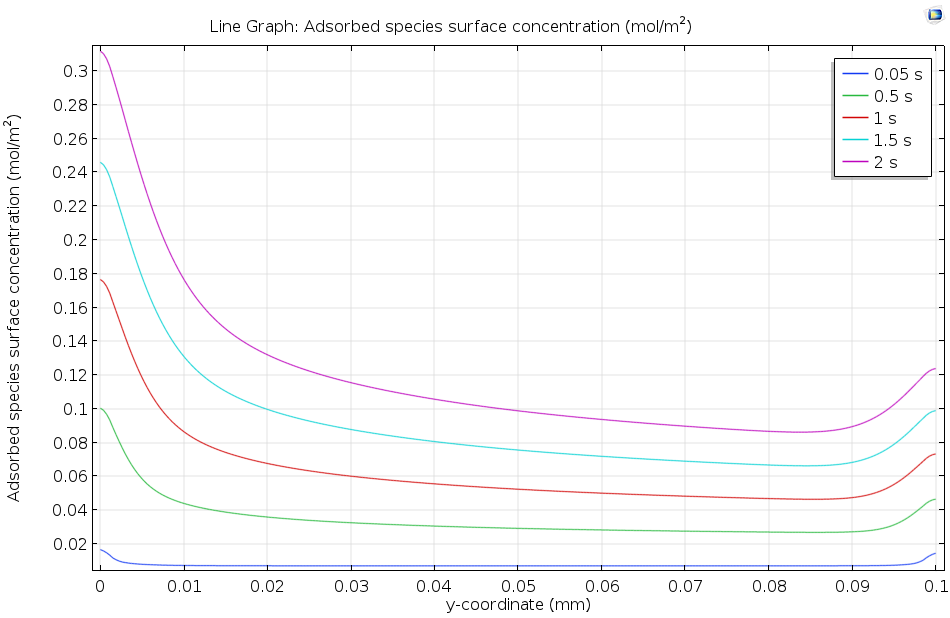
沿吸附剂溶液流过的活性表面长度方向绘制吸附物质的表面浓度。随着时间的推移,吸附物的浓度增加。
关于表面吸附仿真的总结
希望通过学习这个系列文章,您能够了解为什么在化学反应仿真中表面如此重要,以及在 COMSOL Multiphysics 中建立化学模型时,表征表面的不同方法。
了解更多关于使用 COMSOL Multiphysics 模拟化学反应的信息,请单击下面的按钮,联系我们评估软件。
动手尝试
点击下方链接,访问文中介绍的三个示例模型:
参考文献
- P. Atkins and J. de Paula, Physical Chemistry, Oxford University Press.



评论 (0)