
COMSOL Multiphysics® 软件及其附加的“声学模块”提供了线性纳维-斯托克斯接口,支持详细模拟对流动和声学之间复杂的相互作用。COMSOL 5.3 版本新增了一个稳定方案,使功能得到进一步扩展。现在,当系统的声学属性可以由湍流背景流场改变或决定时,您可以对系统进行稳健的仿真;例如汽车的排气系统。在本文中,我们将介绍重要的建模概念,并展示相关应用案例。
气动声学建模入门
稳态背景流场和声场之间复杂的相互作用可以使用“声学模块”中的线性纳维-斯托克斯物理场接口来模拟。此接口支持详细分析流体流动——可以同时是湍流和非等温流——是如何影响不同系统中的声场的。这包括当背景流场与声场发生相互作用时,以及当流场改变声场时发生的所有线性效应。线性纳维-斯托克斯接口不包含流致噪声源项。这些方程基本上求解的是一般形式 CFD 方程的全线性扰动——质量、动量和能量守恒。
对于许多行业和应用领域,模拟与仿真背景流场对声场的具体影响具有重要意义。在汽车工业中,流经的流体会改变排气和进气系统的声学属性,例如,旁路背景流场的大小会影响消声器的传输损耗。在航空航天应用中,衬垫和穿孔板在系统引入流动时的声学性能是一个研究重点。子系统的具体声学属性(吸收、阻抗和反射系数)可以影响整个系统的性能,喷气发动机便是如此。
在消声器和衬垫的示例中,线性纳维-斯托克斯方程也可以捕获背景流场中的湍流所导致的声信号衰减。此外,这些模型中的背景流场通常属于非等温流动。
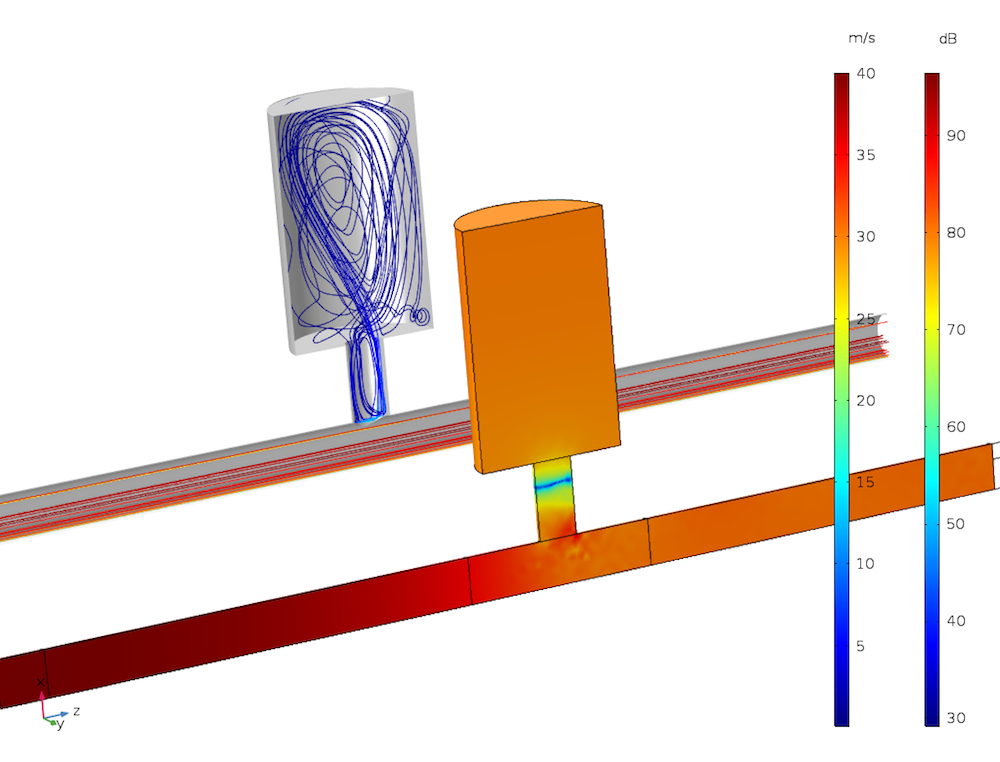
汽车应用的示例。上图显示了基于亥姆霍兹共振器的流场示例的结果。前侧的彩色表面图显示了声压级。后侧流线图显示了背景流场。
线性纳维-斯托克斯接口提供了一个与结构相互耦合的内置多物理场,因此我们能够在频域(或者线性化的时域中)中现成地设置流-固耦合(FSI)模型。在许多应用中,流动、声学和结构振动的相互作用都是重要的考虑因素。一个应用案例是科里奥利流量计的流量感测功能。总而言之,这些接口适用于分析结构在背景流场的流体载荷作用下的振动特性变化。
频域中的流-固耦合示例:在基频下驱动的科里奥利流量计的运动情况。表面显示了结构变形(为了加强可视化效果,我们特意夸大了相位和振幅),管道敞开的切口段显示了管道的内表面声压。
线性纳维-斯托克斯接口还可用于研究燃烧不稳定性和一般的管道内声学,也可以研究更多学术类应用,例如分析流动不稳定性的起始点,或者研究易于发生啸叫的区域。
现在,此接口增加了伽辽金最小二乘(Galerkin least squares,简称 GLS)稳定方案,助力提升仿真的稳健性。新增的默认设置能够更好地处理由控制方程的对流项和反应项引入的数值与物理不稳定性。此外,当使用迭代求解器求解模型时,非常适合使用重新推导后的滑移边界条件。对于必须求解的大型工业问题,这一点至关重要。
线性纳维-斯托克斯方程
线性纳维-斯托克斯方程对描述可压缩、粘性与非等温流体的整套控制方程(线性纳维-斯托克斯方程)的线性化进行了表征。此方程相当于由压力、速度、温度和密度(p0、u0、T0 和 ρ0)定义的稳态背景流场的一阶扰动方程。由此可推导出描述压力、速度和温度(p、u、和 T)——即因变量——的微小扰动传播的控制方程。在扰动理论中,下标 1 有时表示变量为一阶扰动项。控制方程(下标 0 的量表示背景场)写作:
(1)
& \frac{\partial \rho}{\partial t}+\nabla\cdot(\rho_0 \mathbf{u}+\rho \mathbf{u}_0)=M \\
& \rho_0 \left[ \frac{\partial \mathbf{u}}{\partial t} + (\mathbf{u}\cdot\nabla)\mathbf{u}_0 + (\mathbf{u}_0\cdot\nabla)\mathbf{u} \right] + \rho (\mathbf{u}_0\cdot\nabla)\mathbf{u}_0 = \nabla\cdot\mathbf{\sigma} + \mathbf{F} -\mathbf{u}_0 M \\
& \rho_0 c_p \left[ \frac{\partial T}{\partial t} + \mathbf{u}\cdot\nabla T_0 + \mathbf{u}_0\cdot\nabla T \right] + (\rho c_p)\mathbf{u}_0\cdot\nabla T_0 \\
& \qquad -\alpha_p T_0 \left[ \frac{\partial p}{\partial t} + \mathbf{u}\cdot\nabla p_0 + \mathbf{u}_0\cdot\nabla p \right] -(\alpha_p T)\mathbf{u}_0\cdot \nabla p_0 = \nabla \cdot (\kappa \nabla T) + \Phi + Q
\end{align}
其中 Φ = ∇u : τ0 + u0 : τ 是粘性耗散函数;M、F 和 Q 代表可能的源项;κ 是传热系数(国际单位:W/m/K);αp 是(等压)热膨胀系数(国际单位:1/K);βT 是等温压缩率(国际单位:1/Pa);p 是恒定压力下的比热容(单位质量的热容)(国际单位:J/kg/K)。
在频域内,iω 乘子表示时间导数。应力张量和线性化状态方程(密度扰动)的本构方程由下列公式给出:
(2)
\mathbf{\sigma} & = -p\mathbf{I}+\mathbf{\tau}=-p\mathbf{I}+\mu \left( \nabla \mathbf{u}+(\nabla \mathbf{u})^\textrm{T} \right) + \left( \mu_B -\frac{2}{3}\mu \right)(\nabla\cdot\mathbf{u})\mathbf{I}\\
\rho & = \rho_0 (\beta_T p -\alpha_p T)
\end{align}
其中 τ 是粘性应力张量(斯托克斯表达式),μ 是动力粘度(国际单位:Pa s),μB 是体积粘度(国际单位:Pa s)。
我们将傅立叶导热定律应用到能量方程中。您可以在 Acoustics Module User’s Guide 中查阅方程的详细推导过程。然后可以利用线性纳维-斯托克斯,瞬态 接口或线性纳维-斯托克斯,频域 接口在时域或频域中求解方程。
仔细研究控制方程(1),可以看到它们包含了不同类型的项:
- 时间依赖项或频率依赖项(方程中的第一项)
- 扩散项(粘性和热传导造成的损耗)
- u0 ∙ ∇(…) 类型的对流项
- p ∙ (…)、u ∙ (…) 或 T ∙ (…) 类型的反应项
- 可能的源项
由于在接口中求解的是通用方程,这些方程默认模拟声学(可压缩)波、涡旋波和熵波的传播。后两种类型的波依赖于背景流场的速度进行对流,而不以声速传播。声波在传播过程中可以(通过反应项)与流体相互作用,声能量可以传递给声学模式,并从声学模式传递给涡旋模式和熵模式。控制方程中的反应项是引起类似的流动声学耦合的原因。这是因为涡旋波和熵波对背景流场的解产生了非声学(类似于 CFD)扰动,因此在某种程度上,反应项模拟的是 CFD 和声学之间的线性相互作用。
许多气动声学公式忽略了反应项,因为它们也是 开尔文-亥姆霍兹不稳定性 的产生过程的背后原因。这些过程很难进行数值处理。另一方面,如果忽略这些项,则不能对声音衰减和放大进行精确建模。反应项完全包含在线性纳维-斯托克斯接口中。
不稳定性增长在 COMSOL Multiphysics 中有两种处理方式。我们可以通过选择频域而非时域公式来解决随时间增长的不稳定性。如果不能正确地对涡旋模式进行解析,可能出现空间不稳定性,这时可以利用伽辽金最小二乘法稳定方案有效地进行处理。
根据利用线性纳维-斯托克斯方程模拟的不同应用,我们可能需要解析声学、粘性和热边界层。如果存在无滑移和等温边界条件,则需要在固体表面上创建上述边界条件,从而对振荡流进行解析。通常情况下,在大型模型(同边界层厚度相比)中,没有必要考虑边界层的损耗。在液体中,我们通常也可以忽略热边界层,但是气体中一定要添加。通过在壁边界条件下勾选滑移或绝热选项,可以忽略这两种效应。
值得一提的是,我们还能在背景流场和声场之间创建另一个间接耦合。当声波在涉及湍流背景流场的区域中传播时会衰减。只要将 CFD RANS 模型的湍流粘度耦合到声学模型中,即可将衰减效应引入模型。比如说,在分析存在流动现象的消声器系统的传输损耗时,衰减效应是一个重要的考虑因素。
建模注意事项
求解属于计算气动声学(computational aeroacoustics,简称 CAA)领域的线性纳维-斯托克斯方程时,我们需要仔细考虑、理解与处理数值挑战。如上所述,控制方程在物理(开尔文-亥姆霍兹)和数值方面具有不稳定性。由于接口应用了稳定性,那么剩下的关键数值难题就是避免在包含背景场变量(p0、u0、T0 和 ρ0)的项中引入数值噪音。如果反应项的变量存在梯度,尤其需要注意这一点。
如果 CFD 和声学模型采用不同的网格,且/或背景流场和声学问题采用不同的离散化阶次,此问题发生的可能性更大。请注意,我们之所以使用不同的网格或离散化阶次,主要是因为这两个问题需要求解不同的物理场和长度尺度。为了防止此类情况,我们需要谨慎地将背景流场的数据从 CFD 映射到声学模型。这是计算气动声学建模中一个易于理解和描述的步骤。另外,映射步骤可用于平滑 CFD 数据,可以是整体平滑,也可以是特定细节——比如流体动力学边界层——的局部平滑,如果细节对于声学模型不重要的话。
在 COMSOL Multiphysics 中,网格之间的映射由另外的研究步骤来完成。Acoustics Module User’s Guide 和线性纳维-斯托克斯物理场接口的应用教学模型描述了此步骤的详细信息。
使用线性纳维-斯托克斯物理场接口执行仿真时,应考虑以下几点:
- 解析声学边界层:根据所模拟的物理效应和模型大小,判断是否需要对声学边界层进行解析。如果不需要,则将壁上默认的无滑移和等温条件改设为滑移和绝热条件。背景流场的解析细节也会影响这一选择。例如,如果背景流场边界层要实现全解析度,通常需要在声学问题中设置匹配的无滑移条件。
- 网格应该解析 CFD 和声场:重要的几何特征、边界层和大梯度区域应该使用CFD 和声学仿真中的网格来解析。具体而言,声学仿真的网格(如果与 CFD 网格不同的话)应该解析波长和声学边界层(建模请参考上一条)等声学特征,以及背景流场特征。
- 映射:使用映射步骤将 CFD 数据映射到声学问题,尤其当使用不同的网格或离散化阶次时。必要时,可以平滑解,(若声学研究应用了滑移条件)也可以平滑边界层。根据需要,可将背景流场的无滑移条件添加到映射中。
- 离散化阶次:默认情况下,线性纳维-斯托克斯接口对因变量全部采用线性离散化,对于大多数模型这是一个合理的选择。但是,如果应用了无滑移和等温条件,则最好将速度和温度变量切换为二阶离散化。这可以增加壁附近的空间解析度,但是也引入了更多待求解的自由度。
涉及流动的亥姆霍兹共振器
(排气系统中的)亥姆霍兹共振器会使特定的窄频带衰减。系统中的流体流动会改变共振器的声学属性和子系统的传输损耗。亥姆霍兹共振器教学模型研究了主管道中引入流动时的传输损耗(共振器位于主管道的侧分支)。
计算平均流动时,采用马赫数为 Ma = 0.05 和 Ma = 0.1 的 SST 湍流模型。然后使用线性纳维-斯托克斯,频域 接口求解声学问题。接下来,将声学模型与平均流速、压力和湍流粘度耦合。传播损耗的仿真预测与期刊论文的发布数据高度吻合(Ref. 1)。为了准确找到共振位置,并保证传输损耗大小的正确性,模型必须适当地平衡对流项和扩散项。平衡是在模型中实现的。
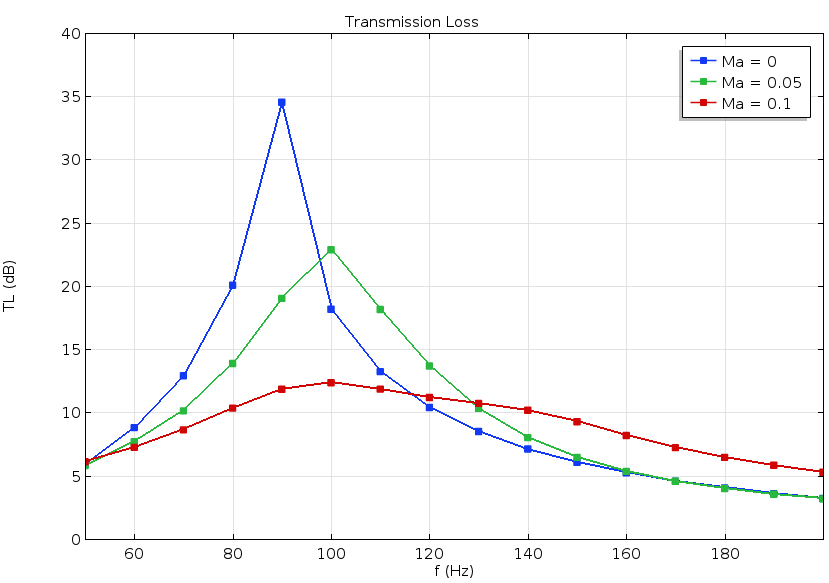
共振器的传输损耗与频率和背景流场的马赫数之间的函数关系。
系统在频率为 100 Hz,马赫数为 Ma = 0.1 时的内部压力分布。平面波从流体上游左侧入射。
切向背景流场中的声学衬垫
在涉及切向背景流场的声学衬垫教学模型中,声学衬垫由八个带微缝的共振器组成,背景切向流场的马赫数为 0.3。衬垫上方的声压级计算结果与研究论文(Ref. 2)发表的数据高度一致。该示例使用“CFD 模块”的 SST 湍流模型来计算流动,并使用线性纳维-斯托克斯,频域 接口计算声传播。然后对声学边界层进行解析,并将默认的线性离散化选项修改为二阶离散化,从而改进壁附近的空间解析度。
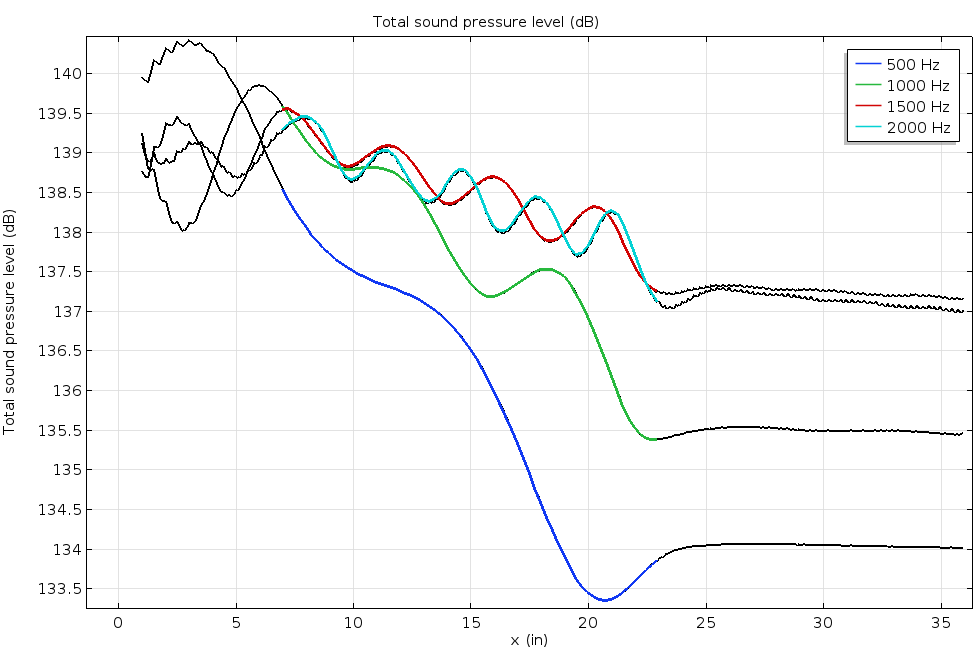
曲线显示了在四个不同的驱动频率下,衬垫上方的表面声压级。曲线的彩色部分突出显示了衬垫的范围。仿真结果与参考研究论文的实验结果呈现出高度一致。
声速波动在衬垫上方作为平面波进行传播,动画显示前四个衬垫。驱动频率为 1000 Hz。彩色图显示速度大小,箭头显示速度矢量。在衬垫表面的小孔附近,流体与声学的相互作用产生了涡流。
科里奥利流量计
科里奥利流量计——又称质量流量计或惯性流量计——可以测量流经此流量计的流体质量流率。该装置还可以计算流体密度以及基于密度的体积流率。科里奥利流量计教学模型演示了如何利用弯曲的几何对通用的科里奥利流量计进行建模。
当流体流经弹性结构(例如弯管)时,它会与弹性结构的震荡运动相互作用。科里奥利效应导致管道上变形的两点之间产生相位差,可用于计算质量流率。
为了对此进行建模,我们借助内置的多物理场耦合,将线性纳维-斯托克斯,频域 接口耦合到固体力学 接口。然后使用湍流,SST 接口来模拟背景平均流动。通过这种方法,我们可以在频域中有效地模拟流-固耦合。
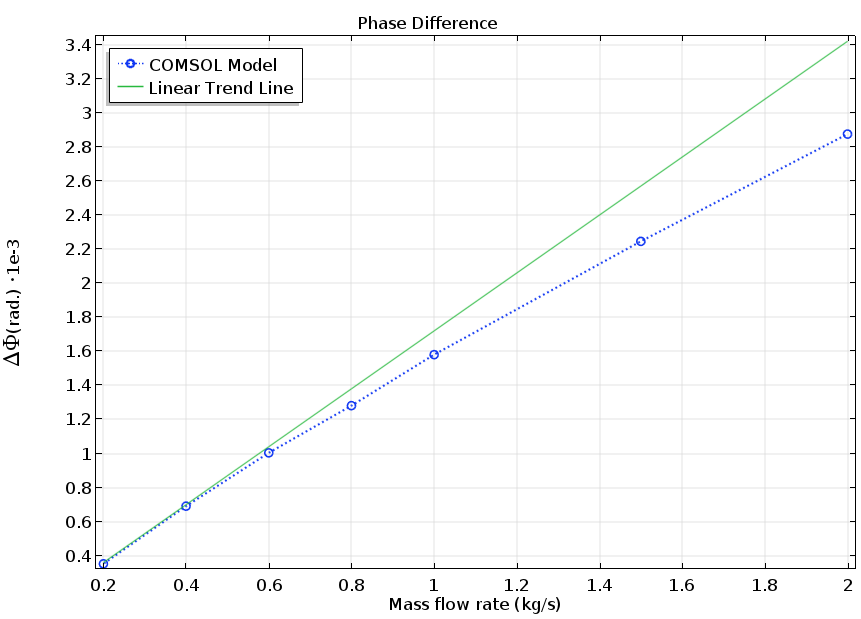
上游点和下游点之间的相差(下面动画中的红点)。图中曲线表示运行科里奥利流量计所需的校准结果。
三个不同的质量流率对应的科里奥利流量计的运动。流量计在结构的固有频率 fd = 163.5Hz 下被驱动。为了增强可视化效果,绘图夸大了变形幅度和相位。随着流率增加,上游和下游的相差随之增大。
了解有关 COMSOL Multiphysics® 的 CFD 和声学仿真的更多信息
- 在“案例下载”中查看下列案例:
- 阅读 COMSOL 用户年会 2016 的展示作品:”Acoustic Scattering through a Circular Orifice in Low Mach Number Flow“
- 查看 COMSOL News 2017 – 声学特辑
参考文献
-
E. Selamet, A. Selamet, A. Iqbal, and H. Kim, “Effect of Flow in Helmholtz Resonator Acoustics: A Three-Dimensional Computational Study vs. Experiments”, SAE International Journal, 2011.
-
C. K. W. Tam, N. N. Pastouchenko, M. G. Jones, and W. R. Watson, “Experimental validation of numerical simulations for an acoustic liner in grazing flow: Self-noise and added drag”, Journal of Sound and Vibration, p. 333, 2014.






评论 (20)
龙龙 黄
2021-08-24尊敬的comsol工程师,一直以来我是学的comsol,后面在研究气动声学时发现咱们这个软件有这个模块,我开始花费大量时间专心学习,后面才发现这个软件在计算气动声学方面并不完善,这浪费了我大量时间,我真心还希望各位不要拓宽软件功能,确实可以处理气动噪声您再宣传
hao huang
2021-08-26 COMSOL 员工感谢您的建议,可以将您觉得需要完善的地方发送到技术支持邮箱:support@comsol.com
闻 张
2021-09-21能不能贴一下原版英文内容啊
hao huang
2021-09-22 COMSOL 员工您好,英文版内容请查看:https://www.comsol.com/blogs/modeling-aeroacoustics-with-the-linearized-navier-stokes-equations/
成 严
2021-10-27I got problems in using linear N-S equations to evaluate the Helmholtz Resonators when the neck is small, for example diameter is 15mm. But, it woks when the neck is relatively big enough. What is the possible mistake I make?
Lei Cao
2021-11-12 COMSOL 员工严成, 您好!
感谢您的评论。
线性NS方程接口中默认求解背景流动以及热黏性损耗。共振腔的颈部直径应该并不会导致结果不正确。可从颈部壁面条件中是否设置为滑移,网格剖分是否能解析几何以及结果梯度等方面进行考虑。
如果有进一步问题,建议您联系COMSOL的技术支持团队:
在线支持中心:cn.comsol.com/support
Email: support@comsol.com
谢谢!
Zhen Liu
2022-04-20工程师您好,请问下面这句话是在哪篇文献里的呢?
仔细研究控制方程(1),可以看到它们包含了不同类型的项:
时间依赖项或频率依赖项(方程中的第一项)
扩散项(粘性和热传导造成的损耗)
u0 ∙ ∇(…) 类型的对流项
p ∙ (…)、u ∙ (…) 或 T ∙ (…) 类型的反应项
可能的源项
由于在接口中求解的是通用方程,这些方程默认模拟声学(可压缩)波、涡旋波和熵波的传播。后两种类型的波依赖于背景流场的速度进行对流,而不以声速传播。声波在传播过程中可以(通过反应项)与流体相互作用,声能量可以传递给声学模式,并从声学模式传递给涡旋模式和熵模式。控制方程中的反应项是引起类似的流动声学耦合的原因。这是因为涡旋波和熵波对背景流场的解产生了非声学(类似于 CFD)扰动,因此在某种程度上,反应项模拟的是 CFD 和声学之间的线性相互作用。
磊 赵
2022-11-22你好,能否提供一下 二维平行板黏性流动中的振动板 这个案例的模型?
Hao Li
2022-12-06 COMSOL 员工您好,由于版本更新原因,该案例暂时下架,请您耐心等待。
http://cn.comsol.com/model/vibrating-plate-in-a-2d-viscous-parallel-plate-flow-18871
彬 刘
2024-07-21这个案例有详细的说明和教程吗
Xiaoming Cai
2024-01-05你好,COMSOL的工程师,我学习了“切向背景流场中的声学衬垫”。在案例中没看到此篇博客中提到的“声速波动在衬垫上方作为平面波进行传播”的动画。请问这个动画怎么绘制出来的,需要另外添加物理场或者研究吗?
Xiaoming Cai
2024-01-05COMSOL的工程师,你好。我在学习“切向背景流场中的声学衬垫”的案例,案例中没有提在这篇博客中的“声速波动在衬垫上方作为平面波进行传播”的动画。请问这个动画是如何绘制的,需要添加另外的物理场或者研究吗?
Hao Li
2024-01-09 COMSOL 员工您好!
感谢您的评论。
动画是后处理计算,无需添加新的物理场和研究。
如“切向背景流场中的声衬”案例中,可以在频域求解的速度绘图{pg12}中添加箭头图,u2,v2,并设置调整箭头绘图特征,然后后处理“导出”节点右键
动画>播放器,设置场景设置为该绘图组{pg12},“动画编辑”设置为“动态数据扩展”,点击“显式帧”即可。若需要将动画导出可以将“目标”改为“文件”。
如果有进一步问题,建议您联系COMSOL的技术支持团队:
在线支持中心:cn.comsol.com/support
Email: support@comsol.com
谢谢!
靖 聂
2024-04-01尊敬的comsol工程师,问一下使用“线性 纳维斯托克斯,频域”这个模块,要怎么设置物理场才能考虑进气体/声场的热粘性损失?
Hao Li
2024-05-16 COMSOL 员工您好!
感谢您的评论。
线性NS方程计算需要输入黏度、比热率等参数,本身已经包含了热黏性损失,不需要特殊设置。
如果有进一步问题,建议您联系COMSOL的技术支持团队:
在线支持中心:cn.comsol.com/support
Email: support@comsol.com
谢谢!
家雨 朱
2024-11-18尊敬的comsol工程师,您好,我之前在官网案例里搜到过瞬态线性纳维斯托克的模型,但是现在找不到了,能麻烦您给找一下链接吗?
Hao Li
2024-11-19 COMSOL 员工您好!
感谢您的评论。
经过查找,目前与Linearized Navier-Stokes相关的案例都是频域下计算,暂无瞬态下Linearized Navier-Stokes的模型。若无法在官网搜索到,可能是该模型已下架,暂时无法分享链接。
昊 宋
2025-03-15工程师您好,请问怎么在“线性纳维斯托克斯瞬态”这个模块下,在计算域内某处加一个声源?以及如何计算在计算域内由于流场扰动引起的声信号?
Hao Li
2025-03-19 COMSOL 员工您好!
感谢您的评论。
线性纳维斯托克斯可直接添加力学条件或者声学条件进行激励,如指定速度或背景声场激励,对于瞬态激励方法与频域形同,可以参考案例 :
[b]流动对亥姆霍兹共振器的影响:流动与声学相互作用[/b]
https://cn.comsol.com/model/helmholtz-resonator-with-flow-interaction-of-flow-and-acoustics-35011
线性纳维斯托克斯主要计算的流体载动声波的效应,流场产生声信号的过程需要lighthill声类比相关的理论,可以参考案例:
[b]腔内流噪[/b]
https://cn.comsol.com/model/cavity-flow-noise-105021
Jack Li
2025-06-26尊敬的comsol工程师,你好,我学习的是频域下的压力声学,计算声音通过结构的传输损耗,现在要给结构表面施加流体载荷,请问这种情况下声传输损耗的仿真应该如何计算,用到哪些模块,有没有比较接近的案例推荐一下?