
在之前的博客文章中,我们向您介绍了解酒泪现象及其起因——马兰戈尼效应。这种效应是由于两相之间的界面处的表面张力梯度引起的。在表面梯度与温度有关的情况下,马兰戈尼效应称为 马兰戈尼对流。本文,我们将演示如何在 COMSOL Multiphysics 中分析马兰戈尼对流,以及如何在仿真中轻松分离重力等效应。
研究马兰戈尼对流的挑战
马兰戈尼对流(也称为热毛细管对流)在许多过程中都很重要,包括焊接,晶体生长和电子束熔化。由于所用金属的类型和所涉及的温度极高,开展分析马兰戈尼对流的试验通常被证明是颇具挑战性的。在这些应用场景中,由于对流效应中混合了马兰戈尼效应和重力的影响,也增加了研究这种现象的难度。
在美国宇航局,为了解质量和热量在微重力条件下如何在流体中移动,研究人员分析了马兰戈尼对流现象。在微重力下进行实验使研究团队能够创建比在地球上大得多的硅油柱,从而更详细地了解其中的流动性和不稳定性。另外,抑制重力的影响有助于消除重力可能引起的变形,从而提高结果的准确性。
通过数值实验,很容易消除实验中无法消除的效应。COMSOL 的马兰戈尼效应教程案例,使用在环境温度下的透明液体来研究马兰戈尼效应导致的速度场,其中材料的热物理已知。由于硅油具有透明性,因此我们可以很容易的将仿真结果与微重力试验结果进行比较。
仿真分析
首先,我们必须求解纳维-斯托克斯方程以对流体中的速度场和压力分布进行建模。需要注意的是,温度变化会直接导致流场速度变化,需要在方程式中考虑浮力影响。这可以通过使用纳维-斯托克斯方程中的布辛涅斯克近似来完成。
使用层流接口,可以求解动量守恒方程。为了求解传热,我们使用了流体传热接口。最后,使用非等温流多物理场耦合来设置传热方程中的对流项,并使用马兰戈尼效应多物理场耦合施加与温度梯度成正比的剪切应力。
教程模型的设置。多物理场节点同时包含非等温耦合和马兰戈尼效应。
此仿真提出了三种必须使用非线性求解器求解的多物理场耦合:
- 由于流体密度的温度依存性 ,导致其遵循布辛涅斯克近似,重力 由包含温度的表达式给出。
- 对流传热取决于动量守恒的速度。
- 马兰戈尼效应将施加在自由表面上的剪切应力与表面温度梯度相关联。
仿真结果
在仿真中,我们分析了垂直壁之间的温差逐渐增加的过程。对于几乎不明显的 1mK 的温度升高,温度场和速度场的关系很小,并且从左到右呈线性下降。
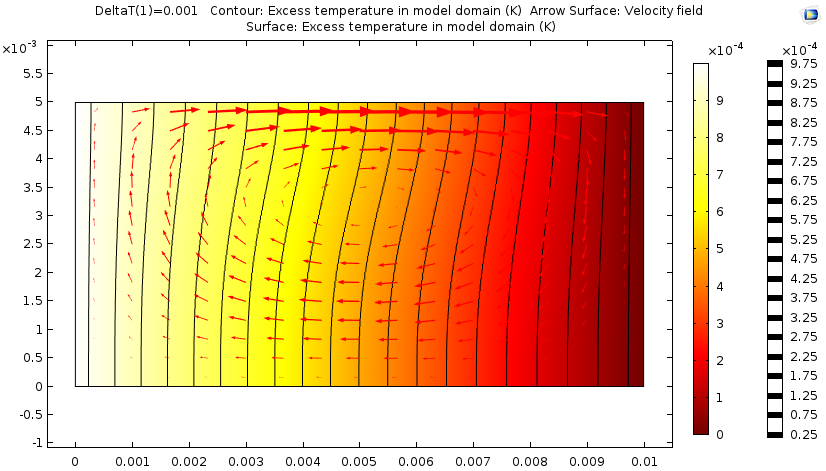
温度仅发生很小的变化后,马兰戈尼效应仿真的结果。背景色表示温度场,红色箭头表示速度场。黑线是等温线。
随着温差增加至 50mK,马兰戈尼效应对流会加速流体流动和温度分布。在整个绘图上,温度下降不再是线性的。
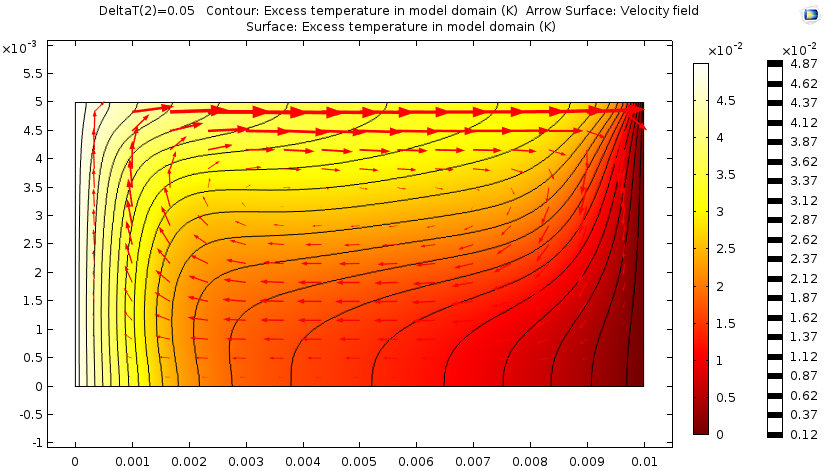
温度升高 50mK 后的仿真结果。
最后,当温差增加至2K 时,温度场和速度场明显耦合,流体在温度梯度最高的边界上加速。
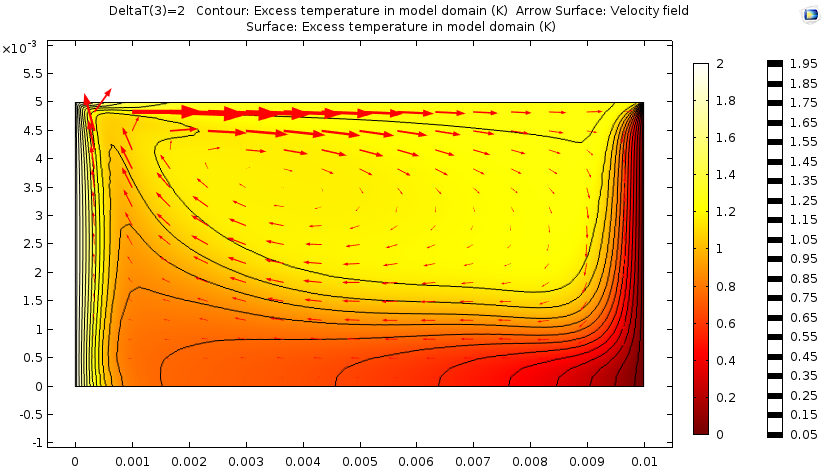
当温差增加到 2K 时的仿真结果。
如上面的仿真结果所示,随着温度差的增加,马兰戈尼效应变得尤为突出。
将重力与马兰戈尼效应分开
对于相同的 2K 温差,我们可以轻松消除重力影响并保持马兰戈尼效应。为了理解浮力如何与马兰戈尼效应进行比较,我们可以简单地禁用表面的马兰戈尼力的贡献,从而使表面没有应力。结果表明,马兰戈尼效应相对于浮力来说,是主要的的流体驱动力。速度曲线在较冷的右壁边界出现一个峰值,这是高普朗特数流体的行为特征。
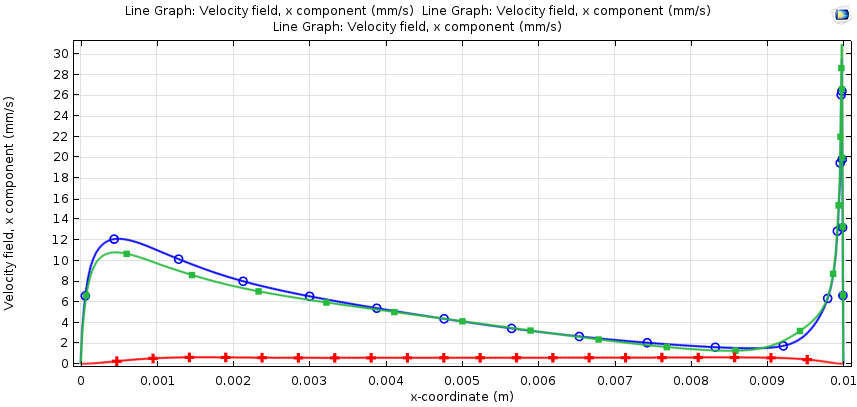
温差为 2K 时,表面水平速度随水平坐标(m)的变化曲线。蓝色表示考虑了马兰戈尼效应和浮力效应的结果。绿色表示只考虑马兰戈尼效应的结果;红色表示只有浮力的结果。
总结
在本篇博客文章中,我们演示了如何建立一个模型来模拟结合重力和马兰戈尼效应的试验场景。在试验环境下,分离这两种效应是具有挑战性的。在数值仿真中,此过程非常简单,有助于理解每一种效应。
您可以通过从我们的案例库下载马兰戈尼效应教程来重现此处展示的结果。本示例使用传热模块中提供的非等温流和马兰戈尼效应多物理场耦合。






评论 (6)
国新 卢
2021-07-23请问有关于Marangoni效应驱动物体运动的案例吗?
hao huang
2021-08-10 COMSOL 员工您好,可以参考文中提到的案例:https://cn.comsol.com/model/marangoni-effect-20329
德一 陈
2024-03-12您好,请问有解决吗
盆 连
2024-10-29请问,做热流耦合固液相变材料中,再相变后施加马兰戈尼效应,按照案例的格式再马兰戈尼效应耦合场内填写 表面张力梯度×温度(与案例一直)的方式做出来的表面张力速度为什么很低 只有3e-3m/s 正常范围应为0.1到1m/s 是什么原因导致呢
Haoze Wang
2024-11-05 COMSOL 员工您好,请将您的模型发送至技术支持中心(https://cn.comsol.com/support),由工程师查看模型设置后回复您。
jj song
2026-02-13在多物理场-马兰戈尼效应-表面张力系数设置单位为N/m,这就是表面张力吧,不是表面张力系数吧