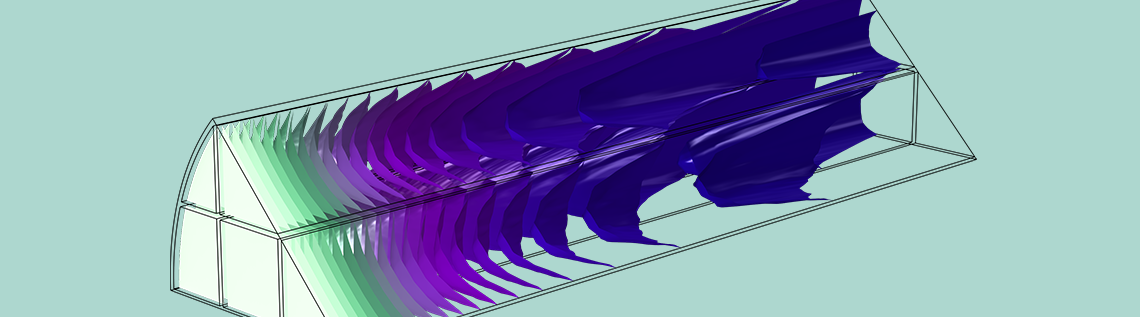
在之前的博客文章中,我们讨论了表面在化学反应器中的特殊性。在本篇博客文章中,我们将讨论如何将反应器结构(如颗粒床)的表面积最大化,以及在固定床反应器具有局部几何复杂性且微观扩散很重要的前提下,我们如何简单而准确地进行模拟。
多孔催化剂和均质模型
当反应发生在表面时,化学反应物的总转化率由化学物质的通量与表面积的乘积给出。因此,表面积越大,整体转化越快。
你可能还记得化学入门知识,化学反应的总速率可以通过增加反应的表面积来提高。一种常用方法是使用含有小颗粒或通道的多孔结构,其中液相化学物质可以通过对流和扩散在孔隙中传递,而孔隙边界则充当活性催化表面。

多孔材料的微观结构。图片由Onnovisser1979提供。在CC BY-SA 3.0许可下使用,通过Wikimedia Commons 分享。本篇博客文章的图片已经被裁剪过。
对多孔介质进行建模时,常使用均匀化方法。与其包含多孔介质的复杂微观细节,不如将其属性平均化表示。另一方面,即使颗粒床的属性已经平均化,我们仍然可以研究颗粒床的不同部分之间的浓度、流速和温度等物理量的变化。有关这种建模方法的更多详细信息,请参阅我同事 Ed 关于异构催化的博客文章。
多孔介质有几个重要属性:
- 孔隙率:空隙(流体)体积与总体积的比率
- 渗透性:流速与流动驱动力的比率,用于量化多孔介质中的表面施加的阻力
- 曲折率:实际扩散长度与点对点位移的比率,量化由非线性扩散路径引起的较低有效扩散率
研究表面反应时,另一个属性变得很重要:比表面积 (SSA) 。这是多孔材料单位体积内的反应表面积。其单位为 m2/m3,或相当于1/m。
在多孔介质的均质模型中,反应速率以多孔材料的单位体积给出。表面上的实际反应速率(Nm, mol m-2 s-1)必须乘以比表面积,得到有效的体积反应速率(Rm, mol m-3s-1):
回想一下本博客系列的第1部分,表面反应的通量通常取决于单位为ms-1的速率常数。然后,多孔介质中一级反应的有效速率可以给出如下:
其中c是反应物浓度(mol m-3),并且
其中km是“真实”速率常数(m s-1)。
从上述方程可以清楚地看出,多孔介质表面发生的非均相反应可以理解为均匀介质中的均相过程,其表观速率与反应的化学动力学和 比表面积成正比。
理想的方形通道反应器:多孔介质属性示例
为了理解多孔反应器不同有效属性之间的关系,我们设想一个简单的例子。下图是一个带平行方形通道的反应器,其中绿色区域是流体,反应可以在与白色区域(固体)的界面处发生。
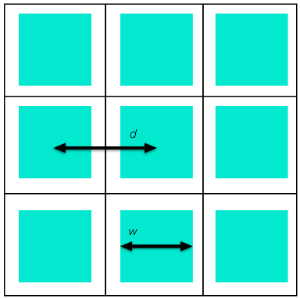
带平行方形通道的反应器的横截面示意图。
我们如何计算这个反应器的比表面积和其他均质属性?反应器横截面具有边长为d的方形单元,其中流体横截面积是一个通道的横截面积,单位长度的有效表面积是一个通道四周的总面积。因此,孔隙率是:
比表面积为
注意,对于相似的孔隙率,正如所料,较窄的通道具有较大的表面积。
渗透率是多少?渗透率可定义为:
有效速度由实际速度与孔隙率的乘积给出。根据方形通道的达西定律,实际速度与粘度 μ 和压力梯度有关 \nabla p:
因此:
因此,对于相似的孔隙率,比表面积的线性增加将导致渗透率的二次降低,所以在相似的超压下流速相应地降低。由于这个原因,多孔反应器的整体化学和机械设计可能需要在流动阻力和总反应速率之间达到良好的平衡的通道尺寸。
最后要考虑的一点是扩散。在计算均匀多孔介质中表面反应的有效动力学速率常数时,我们假设孔隙足够小,以至于扩散可以被认为是局部恒定的。这里的实际要求是什么?
在有流动的存在下,对流通常会主导质量传递,但对流不能决定催化表面的反应限制速率。对于稀释的反应物,进入 表面的流速为零,因此只有扩散才能将材料从整体流动(例如,流动通道的中心线)带到反应表面。如果扩散速率太慢,多孔床的比表面积可能没有得到充分利用。
对于横截面为正方形的通道,可以通过与具有相同横截面积的圆柱体进行比较来分析扩散时间。通道中心线面外扩散所需的时间取决于有效半径的平方:
为了充分利用催化剂表面,我们需要:
因此
其中 U 是平均(实际)速度。
很明显,较小的通道强烈地促进了更好的扩散混合,并提高了多孔介质中可实现的总反应速率。
催化转化器中的多孔介质
上述方形通道反应器类似于催化转化器活性区的总体设计。催化转化器用于分解汽车尾气中的氮氧化物(NOx)等污染气体,在典型的设计中,催化转化器的活性区域称为整体。这是平行的窄通道结构,其中催化剂涂覆在通道表面上(涂层),使气体催化反应的面积最大化。
然而,上述理想的反应器在实际应用中地性能可能会非常差。在整体中,涂层本身是高度多孔的,进一步增加了比表面积,从而提高了总反应速率。因此,上面比表面积的表达式应该用表示涂层微孔率的倍数来增加。
在教学案例氧化氮还原反应动力学分析,整体被表示为多孔域,气流用特征渗透率来描述。由于本例中孔隙沿着整体具有确定的方向,因此不包含曲折率校正。相反,自由流动扩散系数被应用于流动方向上的传递,但是由于形成整体的窄通道的壁,面外方向上的扩散被忽略。
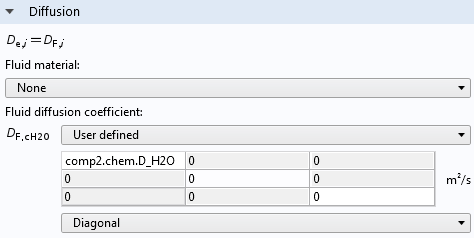
整体反应器模型中扩散系数的各向异性明细表,表示扩散仅发生在微通道方向上,法向平面中为零扩散。
此教学案例将整体中的扩散,对流和反应与使用达西定律的多孔介质流体流动模型相结合,并与一个传热模型耦合,然后将对流与通过多孔整体的固相和气相的热传导耦合在一起。下面,你可以看到催化反应器中 NOx 转化程度的预测,证实这些污染物有很大一部分被去除。
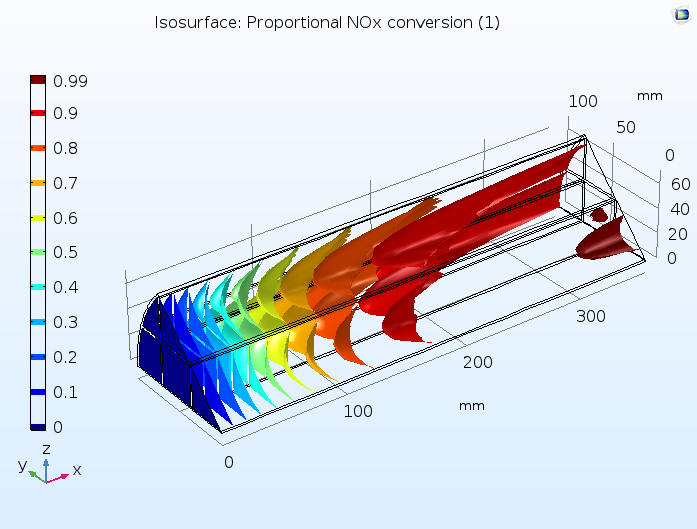
催化转化器整体中 NOx 转化的比例,其中整体被模拟为均匀多孔介质。
反应堆设计人员可以使用 COMSOL Multiphysics® 软件创建详细的多孔反应器模型,以优化流速和催化剂分布,并评估温度依存性,机械应力和设计的其他重要工程方面。
跨尺度均相反应:反应颗粒床
催化转化器的整体是多长度尺度多孔反应器的典型示例。此外,在前面提到的 Ed 的博客文章中,他解释说,组成填充床的催化剂颗粒本身可能是多孔的。每个催化剂颗粒内的微孔产生额外的反应表面积;同时,填充床中的催化剂颗粒之间也存在孔隙,液体或气体可以流过这些孔隙。
组合的微孔-大孔模型的均匀化处理通过“化学反应工程”模块内置的反应颗粒床 特征进行,其中在“稀物质传递” 接口中向二维或三维多孔介质增加了额外维度 的扩散。通常,这个额外维度是近球形催化剂颗粒的半径(或非球形颗粒的有效半径)。
填充床反应器多尺度三维教程模型说明了如何使用反应颗粒床 特征。在它的“设置”窗口的屏幕截图中,你可以看到颗粒的物理属性(如其形状,大小和孔隙率)已指定。注意,这里的“颗粒孔隙率”是指催化剂颗粒本身的微孔率,而不是颗粒床的孔隙率。
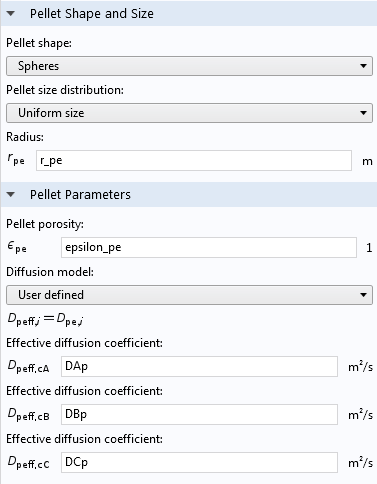
反应颗粒床特征中的颗粒形状、大小、孔隙率和扩散设置。
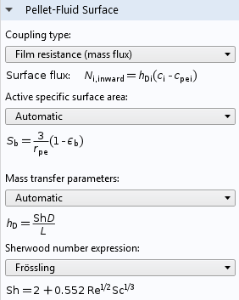
如整体分析中所讨论的,反应物向催化剂颗粒外表面的扩散也很重要,原因是催化剂颗粒之间的多孔流动不会穿透颗粒本身。这意味着存在一个由扩散控制质量传递的边界层,导致在颗粒外表面的平均浓度与颗粒间孔隙的平均浓度之间产生浓度差。反应颗粒床特征定义了预置的扩散膜阻力,它可以根据流动中对流和扩散质量传递的相对贡献的舍伍德数来计算。当然,与 COMSOL Multiphysics 中的任何设置一样,可以使用由用户定义的公式来代替。
为了总结所有涉及的过程,我们设想发生在催化剂颗粒微孔的固-液界面处的一个反应,A(aq) → B(aq)。颗粒本身形成填充床,水溶液在压力下被驱动通过它。传递和反应过程如下:
- A(aq) 从流动入口到多孔填充床的对流主导传递
- 填充床孔隙中的 A(aq) 向催化剂颗粒表面的扩散主导传递
- A(aq)沿微孔的扩散
- A(aq)在微孔表面反应生成B(aq)
- B(aq)沿微孔扩散回催化剂表面
- B(aq) 从催化剂颗粒表面到流过填充床孔隙的溶液的扩散主导传递
- B(aq) 从多孔填充床本体到流动出口的对流主导传递
当然,我们不应该认为这些过程是顺序进行的——它们都在同一时间发生,而反应器是在连续运行的。这些步骤中的任何一个,无论是反应速率本身还是组分质量传递过程,都可能会限制 A 到 B 的总转化率,从而决定了反应器的最大生产能力。由于化学物质传递问题涉及许多步骤,因此数值仿真对于预测现象和优化效率至关重要。反应颗粒床 特征支持根据反应器的物理和化学性质快速定义这种仿真。
下图显示了反应颗粒床模型的典型输出。第一个图显示了反应物浓度在反应颗粒之间的孔隙空间上平均分布。当反应物扩散到颗粒中并发生反应时,反应物浓度从左到右被消耗掉。左侧的流动入口模式导致浓度分布不均匀,因此催化剂的利用不均匀。
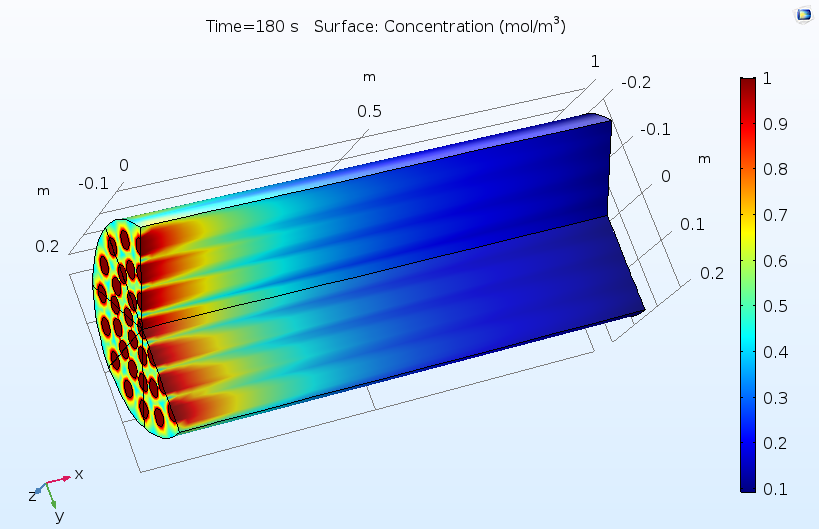
反应颗粒床中反应颗粒间孔隙中反应物的平均浓度。
下面的数据显示了颗粒床的更定量的分析,分析了反应物 A 和 B 以及产物 C 的孔隙和颗粒浓度。产物 C 的颗粒浓度不均匀,最大值出现在颗粒床的中间,表明催化反应在催化剂床的特定区域进行得更快。对填充床中的反应区范围以及其位置如何随时间变化进行评估,可以确保催化剂的最大利用效率和反应物到产物的最佳总转化率。

反应颗粒床中反应颗粒之间以及反应颗粒内反应物 A 和 B 以及产物 C 的平均浓度。
多孔介质和反应颗粒床表面反应的总结性思考
在这个博客系列的第一篇文章中,我们强调了表面作为化学反应场所的特殊属性。实际的化学工程设计通常涉及多孔介质和微孔催化剂颗粒,以使表面积最大化。“化学反应工程模块”是 COMSOL Multiphysics 的一个附加模块,它的专用特性使多孔材料表面发生的反应和质量传递(以及与流动和传热的耦合) 公式变得简单。
其他资源
- 尝试操作本篇博客文章中提到的教程模型:
- 阅读本博客系列中关于表面反应建模的第1部分






评论 (28)
wallace chi
2023-11-30你好,我现在需要模拟多孔CaO固体与CO2的吸附反应,CO2气体的含量变化可以通过物质传递接口描述,想请问一下如何才能得到固体的含量变化呢?
Yi Li
2023-12-06 COMSOL 员工您好,根据质量守恒定律,气体的减少量应该等于固体的增加量,您可以通过在后处理提取CO2的反应量来得到固体的增加量,也可以在仿真时自定义变量,对该值进行计算,您也可以将问题和模型发送至技术支持中心:https://cn.comsol.com/support。由工程师结合模型回复您。
博士 童
2024-05-30您好,请问您是用稀物质传递中的填充床缩芯反应模型做的吗
腾 庞
2025-05-20您好,请问是用什么模型模拟的固气反应
HH 潘
2025-11-21您好!请问可以联系我一下吗?关于这方面的问题想请教您一下,qq297495838
琼德 张
2024-01-10你好,请问多孔介质中非均匀孔隙率应该如何设置呢?
yongchao wang
2024-01-17 COMSOL 员工孔隙率可以写成空间坐标的函数,这样不同位置的孔隙率也就不同了。
飞 王
2024-01-11你好,我想模拟多孔介质内填充物的分解以及分解后气体在多孔介质内流动的传热传质过程,请问是否可以实现这种模拟内容以及是否有相关案例进行参考,非常感谢。
yongchao wang
2024-01-17 COMSOL 员工可以实现,当填充物质分解成气体后会导致孔隙率变大,可参考《多相催化中的碳沉积》案例,此案例是物质沉积与分解是反向的:https://cn.comsol.com/model/carbon-deposition-in-heterogeneous-catalysis-1968
永超 隽
2024-03-04comsol的工程师你好,蛇形反应流道和蛋白质吸附这两个案例都是稀物质传递,我想问一下,我在做浓物质传递时没有稀物质传递的“表面反应”这个节点,但是浓物质传递中多了两个默认节点“通量”和“通量不连续”,我有点不太理解这两个节点的意思,可以方便解释一下吗?除此之外,浓物质传递物理场有个“表面平衡反应”节点,这个和稀物质中的“表面反应”是一个意思吗,我看设置窗口中的方程也不一样、设置也不一样,有何异同。望收到回复,谢谢
Xiaohan Jiang
2024-03-06 COMSOL 员工通量边界在浓物质、稀物质传递接口中均匀内置的,这两个应用场景是一致的。通量不连续是应用于内部边界,例如管道中的过滤网、薄膜等,指定的是该边界两侧的通量之差。稀物质物理场中也有一个表面平衡反应特征,这与浓物质传递中的一致,关键的定义参数就是反应的平衡常数。表面平衡反应与稀物质中的表面反应不完全是一回事,表面反应特征使用的场景更多,例如正反应、负反应等都可以设置。关于这几个边界的进一步详细的说明,您还可以查阅化学反应工程模块 User Guide 中的介绍。
劲斌 张
2024-03-12能用来模拟回转炉中用乙炔包覆硅氧负极吗?
yongchao wang
2024-03-18 COMSOL 员工您描述的过程应该是在保护气体环境下实现硅氧负极的表面包覆,会在硅氧负极颗粒表面发生反应(颗粒可能会增大),并且颗粒间会有物质的输运及浓度分布,可以应用填充床的缩芯模型进行描述,可参考案例《通过参数估计研究木材热解》,案例模型随着反应颗粒减小,与您的场景相反,但是建模的思路是相同:https://cn.comsol.com/model/pyrolysis-of-wood-118991
腾飞 马
2024-04-11你好,我想在固定床中加一个气体选择性透过膜,去除物质,想请教以下咋设置?用哪个接口
yongchao wang
2024-04-19 COMSOL 员工膜的选择性透过可以用物质传递接口进行描述,具体实现的思路可以参考案例《透析分离》:https://cn.comsol.com/model/separation-through-dialysis-258
博士 童
2024-05-30工程师您好,我想模拟颗粒A受热分解为颗粒B和气体C,请问是要用稀物质传递中的填充床缩芯反应模型做吗,但是不明白怎么设置颗粒A的初始质量。可以解答下吗?
Xiaohan Jiang
2024-05-31 COMSOL 员工不一定要使用缩芯反应模型,对于固体物质的消耗与生成,可参考 https://cn.comsol.com/model/pyrolysis-of-wood-118991。该案例通过一个全局 ODE 来定义的固相中的物质浓度或密度,并与多孔中的气相反应相耦合。
博士 童
2024-05-31谢谢jiang老师,如果我把一堆颗粒反应物都看成气体,用多孔介质中稀物质传递中填充床的多孔催化剂模型可行吗?
Xiaohan Jiang
2024-06-03 COMSOL 员工可以试下,如果是气体的话则可能会考虑扩散、对流的问题,如果是固体则没有扩散、对流效应。
博士 童
2024-06-14jiang老师 再次打扰,我可否将我设置好的算例发您检查下,我用的域常微分方程,但是感觉还是不太对。
hao huang
2024-06-19 COMSOL 员工您好!
感谢您的评论。
如果有进一步问题,建议您联系COMSOL的技术支持团队:
在线支持中心:cn.comsol.com/support
Email: support@comsol.com
谢谢!
思仪 李
2024-06-28你好,我也遇到了这方面的问题,请问您最后是怎么解决的呀
正琦 焦
2024-08-15你好,我想模拟外部加热的填充床中化学反应的放热温升,是否要在“流动传热”物理场中为“多孔介质”添加热源选项?如果添加热源选项,有颗粒热源和反应热源两种选择,应该如何选择呢?
yongchao wang
2024-08-21 COMSOL 员工在“流体传热”下的“多孔介质”设置窗口需要选择多孔介质类型为“填充床”,外部加热应该用边界热源设定,一般应该是对反应器壁进行加热,所以用“流体”中的边界热源定义;对于化学反应,要根据反应发生的位置进行热源的定义,对于填充床反应一般发生在颗粒内部的孔隙内,所以可以使用“颗粒”下的热源进行定义。
玉轩 季
2025-04-30请问此处有效反应速率常数keff,m的单位是m/s,根据公式keff,m=km*SSA,其中SSA的单位是m2,那么km的单位应该是m-1*s-1么
Yi Li
2025-05-07 COMSOL 员工SSA的单位是1/m,km的单位m/s
腾 庞
2025-05-20请问固气反应的模型应该如何利用多孔介质建模
yongchao wang
2025-05-26 COMSOL 员工1.如果固体与气体界面用几何描述,则可以用“表面反应”进行描述;2.如果固体是多孔结构,只存在颗粒与颗粒间的孔隙,描述固气反应时可用“多孔介质中的浓物质传递”接口,并添加“催化剂”节点进行描述;3.如果固体是多孔结构,不仅存在颗粒与颗粒间的孔隙,颗粒内部也存在孔隙,那么可以使用“填充床”下的“浓物质传递”进行描述;可分别参考如下模型:https://cn.comsol.com/model/carbon-deposition-in-heterogeneous-catalysis-1968
https://cn.comsol.com/model/a-multiscale-3d-packed-bed-reactor-17019