
在例如碳纤维等聚合物复合材料的制造过程中,一个关键的阶段是聚合物树脂与纤维状多孔(可渗透的)增强材料的渗透。传统上,渗透率是通过实验来测量的,但这种方法既昂贵又耗时。今天这篇博客,我们将介绍如何利用 COMSOL Multiphysics® 软件快速、准确地建立理想的增强复合材料的渗透系数模型,以成功提高产品质量。
高分子复合材料
碳纤维增强聚合物(CFRP)等高分子复合材料由于高性能和低质量而能够大幅降低燃料和能源消耗,被广泛用于航空航天、汽车和风力涡轮机行业。碳纤维增强聚合物复合材料由两种材料组合而成。
- 主要提供抗拉强度的纤维结构增强材料,例如碳纤维
- 帮助在纤维之间传递载荷,同时提供压缩强度聚合物树脂,例如环氧树脂

展示了碳纤维结构和电动机的BMW i3® 插电式混合动力概念车的剖面图。图片已通过Wikimedia Commons获得许可(CC BY-SA 3.0)。
增强材料在被排列成增强织物前,例如基于要制造的组件在长度尺度上单向或编织排列,其结构通常由直径约为 10 μ m 的单根纤维形成的成千上万根纤维,即纤维束组成。
在制造过程中,聚合物复合材料通过例如树脂传递成形(RTM)等工艺形成,包括在树脂固化之前将黏性聚合物树脂渗透到多孔(可渗透的)增强材料中。在这个阶段,树脂的流动在宏观尺度(组件的长度尺度)和微观尺度(纤维的长度尺度)上发生,其中流动可以在内丝束间发生,也可以在丝束间发生。
理解增强材料的渗透率很重要,它可以帮助:
- 提高充模(渗透)阶段模拟的准确性
- 优化注射压力等工艺参数
- 通过减少缺陷(例如未渗透区域、干点、纤维移位、丝束内和丝束间空隙形成以及称为竞流 的不均匀过滤),来提高最终产品质量
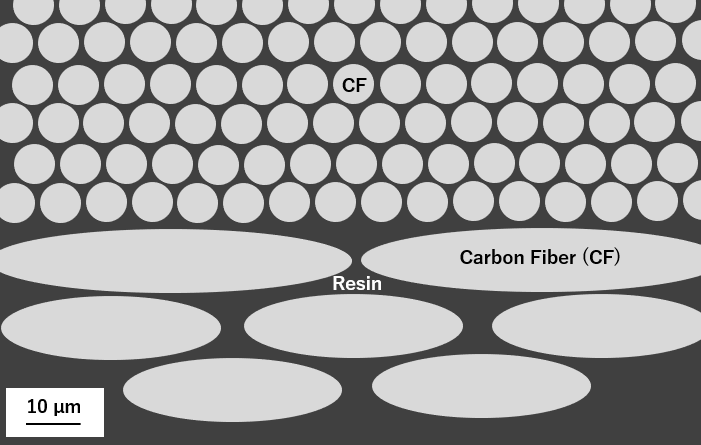
横截面图像显示了碳纤维在树脂中的典型结构、分布和尺寸。
清洁水和达西的贡献
1856 年,水力工程师亨利·达西 (Henry Darcy)在致力于改善法国第戎市(Dijon)的水质时,出版了The Public Fountains of the City of Dijon。在这部著作中,他描述了一个描述牛顿流体在宏观上通过均匀多孔介质的饱和层流的方程。这个方程就是达西定律,被广泛用于水文学应用中,并被用于模拟 RTM 工艺的模具填充阶段。达西定律的定义如下:
其中,\mathbf v 是表面速度(在宏观尺度上观察),\mu 是动态黏度,\mathbf K 是织物的渗透率,P 是压力(尖括号表示体积平均)。
渗透率 \mathbf K 是以面积为单位的张量,表示流体流过多孔介质的难易程度。
模拟复合增强材料的渗透率
让我们以一个理想的单向复合增强材料为例,通过将纤维束表示为排列在正方形周期阵列中的实心(不可渗透的)圆柱体来模拟横向无量纲渗透率。这种方法允许我们通过与已发表的解析解和实验结果进行比较来验证COMSOL Multiphysics的仿真结果。
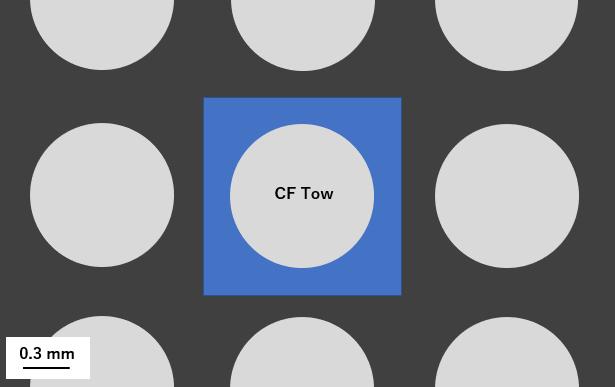
横截面图显示了理想的复合增强材料,碳纤维丝束呈方形周期性阵列,蓝色域代表基本单元。
理论
我们可以通过求解围绕圆柱体的基本单元(上图中的蓝色区域)中 纳维-斯托克斯方程的稳态解,获得圆柱体横截面的方形周期性阵列横向流动的解。但是应该注意的是,对于非常低的雷诺数流,\mathbf Re\ll1,我们还可以在 COMSOL Multiphysics 中通过求解斯托克斯或蠕动流方程来获得解。
模型概述
基本单元模型的设置和边界条件的施加。使用周期性流动 条件和压力点约束,从左侧边界到右侧边界施加一个单位压降。然后在顶部和底部边界施加对称 条件,在圆柱体的边界施加无滑移壁 条件。用一个单位值定义流体的密度 \rho 和动态黏度 \mu 。
由于我们要计算圆柱体面积分数 a\scriptstyle f 从 0.05 到 0.7 的无量纲渗透率,因此可以对几何形状进行参数化,并在一次计算中对所有值进行参数化扫描。网格设置为物理场控制的极细单元尺寸,因此当圆柱体面积分数很高并且圆柱体几乎彼此接触时,我们可以用极细的网格求解相邻圆柱体之间的高速度梯度问题。
渗透率相对于圆柱半径的长度尺度无量纲化,然后通过包括阻力系数的倒数 Cd=\frac{F}{\mu \overline{\mbox{u}}} 的公式计算:
{u}}}{F}
其中, F 是压降和垂直于压降方向横截面积的乘积。
结果
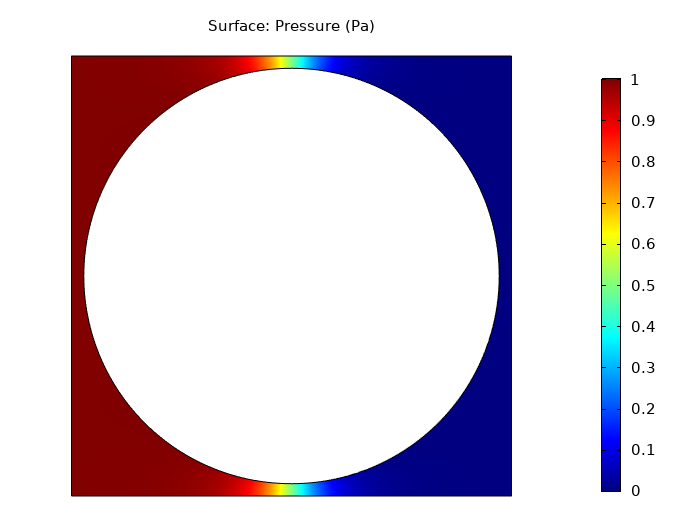
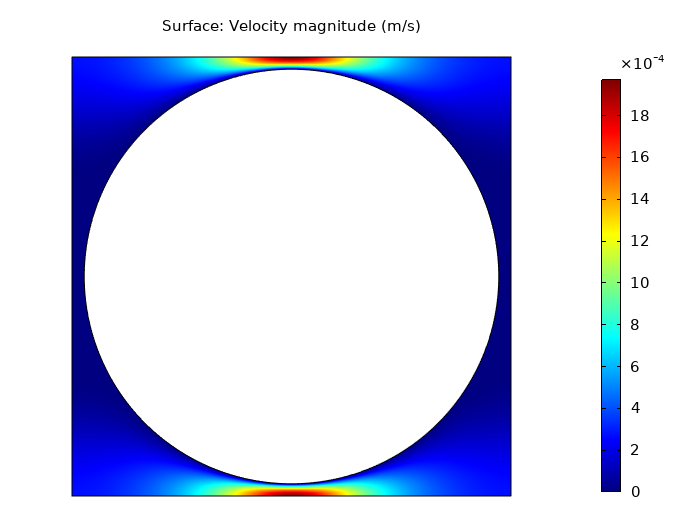
仿真结果如下图所示。压力和速度梯度在邻近圆柱体的区域中最高,流体流动间隙最小。
仿真结果显示了方形周期性圆柱阵列,实心面积的分数a\scriptstyle f=0.7 时的流动压力等值线(左)和速度等值线(右) .
将无量纲渗透率的结果 K_{non} 与基于实心圆柱体的已发表的理论解析解和实验值进行比较,结果显示出实心面积分数 a\scriptstyle f 在较宽的范围内具有极好的一致性,结果显示随着 a\scriptstyle f 的增加,渗透率呈非线性下降。
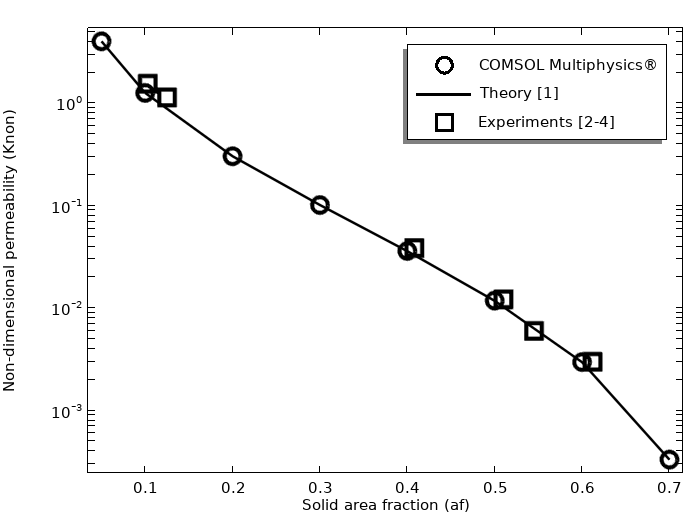
仿真结果显示了无量纲渗透率与方形周期性圆柱体横截面阵列流动的理论和实验结果比较。
结束语
在这篇博客中,我们介绍了如何使用 COMSOL Multiphysics 快速、准确地模拟理想化复合增强材料的渗透率,并通过与已发表的理论解析解和实验值进行比较来验证仿真结果,最终结果显示出模拟值与二者具有极好的一致性。该模型为平行流和更复杂的丝束形状(包括丝束内渗透率)的渗透率分析奠定了基础,为复合材料的制造和优化开发提供了更准确的模拟。
除了模拟复合增强材料的渗透率之外,COMSOL Multiphysics 还可用于模拟预测其他各种多孔材料的渗透率。
下一步
- 尝试自己动模拟文中的教程案例
参考文献
- A.S. Sangani, and A. Acrivos, “Slow flow past periodic arrays of cylinders with application to heat transfer”, International Journal of Multiphase Flow, vol. 8, no. 3, pp. 193–206, 1982.
- L. Skartsis, B. Khomami, and J.L. Kardos, “Resin flow through fiber beds during composite manufacturing processes. Part II: Numerical and experimental studies of Newtonian flow through ideal and actual fiber beds”, Polymer Engineering and Science, vol. 32, no. 4, pp. 231–239, 1992.
- T.A.K. Sadiq, S.G. Advani, and R.S. Parnas, “Experimental investigation of transverse flow through aligned cylinders”, International Journal of Multiphase Flow, vol. 21, no. 5, pp. 755–774, 1995.
- A.A. Kirsch and N.A. Fuchs, “Studies on fibrous aerosol filters-II. Pressure drops in systems of parallel cylinders”, Annals of Occupational Hygiene, vol. 10, pp. 22–30, 1967.
- S. McCallum, “Experimental, Analytical and Computational Studies in Resin Transfer Moulding”, in Department of Materials. 2003 Thesis (PhD), Imperial College of Science Technology and Medicine, London, UK.
BMW i3 是 Bayerische Motoren Werke Aktiengesellschaft 的注册商标。






评论 (0)