
今天的客座博主是来自Lightness by Design公司的 Björn Fallqvist 博士,他在文中讨论了分析热机械疲劳的不同考虑因素和方法。
在这篇博客文章中,我们研究了 COMSOL Multiphysics® 软件中用于分析热机械疲劳的相关材料模型(模型使用了来自热机械疲劳测试的实验数据,以及参考文献中的材料参数)。随后,对在高温下运行的压力容器进行了分析,并使用非线性连续疲劳损伤模型评估疲劳寿命。
为什么要分析热机械疲劳?
在许多应用中,传统的等温疲劳分析是不够的,因为部件在高温下或在高温循环下工作时,材料性能与室温有很大不同。这种应用的典型例子是涡轮机和发电厂部件。
传统的疲劳分析,尤其是高周疲劳(high-cycle fatigue,HCF),不能直接考虑高温造成的影响。在高周疲劳区域中,载荷较低,蠕变等影响可以忽略不计。有时,S-N 曲线会减小,以解决温度升高时疲劳强度降低的问题。然而,这没有考虑到温度和载荷同时循环时的影响,即所谓的热机械疲劳。这种温度变化的影响在低周疲劳(low-cycle fatigue,LCF)区域中尤为重要,在该区域,需要考虑多个方面,主要是弹塑性和蠕变的材料性能变化。
评估高温下疲劳性能的一种方法是使用样品在多个温度下的稳定(通常是寿命中期)应力-应变曲线,以获得应力或应变幅度,并确定控制非线性应力-应变曲线的硬化参数。理论上,人们可以用一组特定的外加载荷和温度组合进行实验,并尝试根据实验结果估算疲劳寿命。然而,热机械疲劳测试需要相对较长的时间,并且成本较高。评估高温下疲劳能力的一种更方便的方法是使用描述应力水平和失效循环关系的解析表达式,并根据温度对其进行修正。
热机械疲劳试验
在热机械疲劳试验中,试样通常同时承受循环应变和循环温度。这可以是同相(IP)或异相(OOP)。对于前者,最大拉伸载荷与最高温度同时出现,对于后者,最大拉伸载荷出现在最低温度时。
为了与本篇博文中的实验结果进行比较,我们参考了参考文献 1,其中研究了 P91(一种常见的电厂用钢) 的热机械疲劳。我们从参考文献 2 中获得了模型材料参数,获得了应力-应变曲线。值得注意的是,对于参考工作,使用统一的模型(即黏塑性应变由塑性和蠕变分量组成)。然而,这只会影响模型蠕变部分的值。
热机械疲劳分析的材料模型
作为温度的函数的材料模型参数(参考文献2)如下表所示:
| Temp [°C] | E [MPa] | k [MPa] | Q [MPa] | b [-] | a1 [MPa] | C1 [-] | a2 [MPa] | C2 [-] | Z [MPa s1/n] | n [-] |
|---|---|---|---|---|---|---|---|---|---|---|
| 400 | 187,537.0 | 96 | -55.0 | 0.45 | 150.0 | 2350.0 | 120.0 | 405.0 | 2000 | 2.25 |
| 500 | 181,321.6 | 90 | -60.0 | 0.6 | 98.5 | 2191.6 | 104.7 | 460.7 | 1875 | 2.55 |
| 600 | 139,395.2 | 85 | -75.4 | 1.0 | 52.0 | 2055.0 | 463.0 | 463.0 | 1750 | 2.7 |
表 1 作为参考的材料参数
参数 a 和 C 与非线性运动硬化模型有关,E 是弹性模量,k 是初始屈服应力,Q 和 b 是各向同性硬化参数, Z 和 n 是黏塑性流动速率的材料参数。
这些将在下面的章节中阐述。综合起来,这些参数决定了屈服面在应力空间中的平移和膨胀/收缩。模型中的所有参数值都在温度之间进行插值。后续章节中,我们将介绍这一点的实现。
黏塑性
根据参考文献5,通过使用黏塑性 Chaboche 公式计算粘塑性应变张量的速率,考虑了速率相关效应
这里,A 是速率因子(设置为等于 1/s),F 是屈服函数),nD 是应力偏离的张量方向,n 是材料参数,是参考应力值。
经检验,COMSOL Multiphysics 参数 σref 和 n 分别等于表 1 中的 Z 和 n,。屈服函数 F 被定义为
这里,R 是屈服面的增加,k 是初始屈服应力,是运动硬化引起的背应力张量。
选择函数 φ 作为 von Mises 等效应力。
各向同性硬化
屈服面尺寸 σy 的各向同性硬化定律(Voce)被定义为
其中,σsat 是大塑性应变下屈服面尺寸的饱和应力,β 是材料参数,是等效黏塑性应变。
根据这个公式,取决于饱和应力值,屈服面可能会随着塑性应变的增加而膨胀或收缩。COMSOL Multiphysics 中的参数 σsat 和 β 分别 对应于表 1中的 Q 和 b。
运动硬化
所选择的非线性运动硬化定律是 Chaboche 硬化,其中背应力张量由 j 个 Armstrong–Frederick 非线性硬化项的分支叠加组成:
第一项是初始运动硬化模量,在我们的分析中忽略不计。与参考文献1–2中使用的公式相比,COMSOL Multiphysics 中的两个分支硬化参数 C 和 γ 分别是 Ca 和 C。
蠕变
如前所述,在参考文献中,作者使用了统一的黏塑性模型,直接定义了黏滞应力。在COMSOL Multiphysics中,我们使用Norton蠕变模型计算蠕变应变率:
这里,Ac 是速率因子,σeff 是等效应力,σref 是基准应力值(设定为 1MPa),nc 是材料参数。这些参数的值来自参考文献6。
在 COMSOL Multiphysics® 中使用的材料参数汇总
分析中使用的材料参数汇总如下(表2)。请注意,在大多数情况下,参数名称已经更改,以反映 COMSOL Multiphysics 中的标签。而且,常数 C 的定义与中参考文献使用的定义不同,因此它们采用不同的值。
| Temp [°C] | E [MPa] | \sigma_{ys0} [MPa] | \sigma_{sat} [MPa] | β [-] | C_1 [MPa] | \gamma_1 [-] | C_2 [MPa] | \gamma_2 [-] | \sigma_{ref,vp} [MPa s1/n] | n [-] |
|---|---|---|---|---|---|---|---|---|---|---|
| 400 | 187,537.0 | 96 | -55.0 | 0.45 | 352,500 | 2350.0 | 810,000 | 405.0 | 2000 | 2.25 |
| 500 | 181,321.6 | 90 | -60.0 | 0.6 | 215,870 | 2191.6 | 863,810 | 460.7 | 1875 | 2.55 |
| 600 | 139,395.2 | 85 | -75.4 | 1.0 | 106,860 | 2055.0 | 810,250 | 463.0 | 1750 | 2.7 |
表2 COMSOL Multiphysics 中使用的材料参数。
蠕变参数 A_c=2.4623 \cdot 10^{-21}/h,\sigma_{ref,cr}=1 MPa,n_c=7.538,泊松比 0.3,热膨胀系数 \alpha=14.5 \cdot 10^{-6}/^{\circ}C,在所有温度下都相同。请注意,蠕变参数是在873 K下测量的,尽管COMSOL Multiphysics中也包含温度依存性。
非线性连续损伤疲劳模型
背景
我们在疲劳分析中使用的疲劳模型是 Chaboche 提出的非线性连续疲劳损伤模型(参考文献3)。这种模型很有吸引力,因为它的易用性,并且对于低循环疲劳和高循环疲劳(适用于钢)都有效。简而言之,它是基于以下形式的速率损失方程
损伤变量 D 相对于循环周期 N 的比率取决于最大应力 \sigma_M,平均压力 \bar\sigma,以及当前的损坏。通过对函数 f 的特定选择,最终得到(这里省略了推导)与失效循环数 NF 的关系:
这里,a 和 \beta_{fat} 是材料参数,\sigma_u 是极限抗拉强度,根据下面公式,\sigma_l 是平均应力的疲劳极限 \bar\sigma:
这里,b_{fat} 是材料参数。
最后,M\bar{(\sigma)} 被定义为
其中,M_0 为材料参数。
在热机械疲劳中,当温度 T 发生变化时,有效温度(T *)可以根据以下公式在一个循环周期内计算:
本质上,有效温度 T * 被认为是计算相同循环次数 NF 的温度,即极端温度在某个时间跨度内的平均循环次数。
疲劳数据和假设
在室温下,P91 钢的极限抗拉强度为 600MPa(参考文献7),疲劳极限约为 420MPa(摘自 参考文献6,以及在不同应力水平下的失效循环次数。这些可以用来确定由Chaboche疲劳模型(图1)定义的S-N曲线的最小二乘拟合。这里,载荷比 R(R=\frac{\sigma_{min}}{\sigma_{max}},最小应力与最大应力之比)为 R = -1; i.e., \bar\sigma=0, M\bar{(\sigma)}=M_0 和 \sigma_l(\bar\sigma)=\sigma_{l0} 用于参数确定。
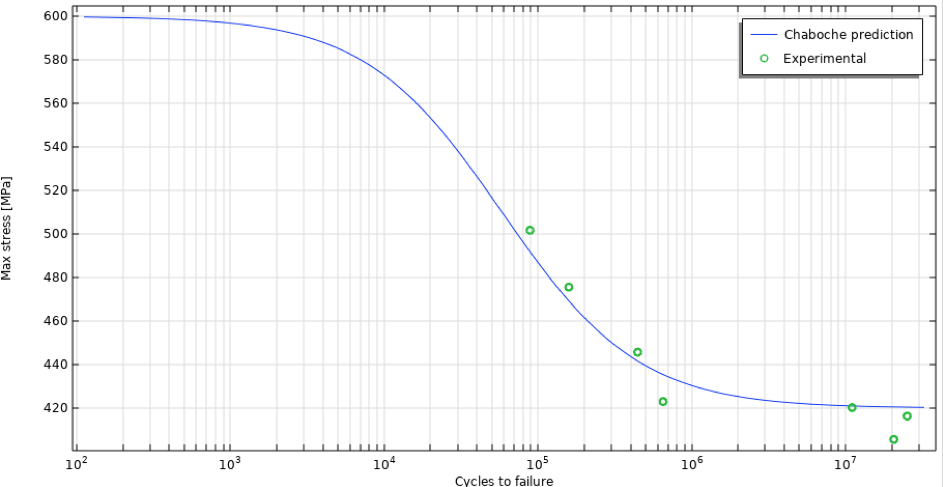
图1 由 Chaboche 疲劳模型定义的 S-N 曲线。
结果参数 a = 9 \cdot 10^{-6}, \beta_{fat}=0.287, 和 M_0=54.3MPa。
理想情况下,中间区域需要更多的点来完全定义曲线,但是对于方法演示来说,这就足够了。由于考虑热效应是至关重要的,因此 S-N 曲线必须按比例缩放。有几种方法可以做到这一点,最合适的方法是利用不同温度下的曲线,获取每个温度下的材料参数,然后对这些参数进行插值。但是,由于缺乏此类数据,因此根据参考文献 1 中的图 3.24 定义的折减系数,可以非常方便地来缩放极限抗拉强度和疲劳极限。所得的 S-N 曲线如图 2 所示。注意,这些都是针对 R=-1 的。
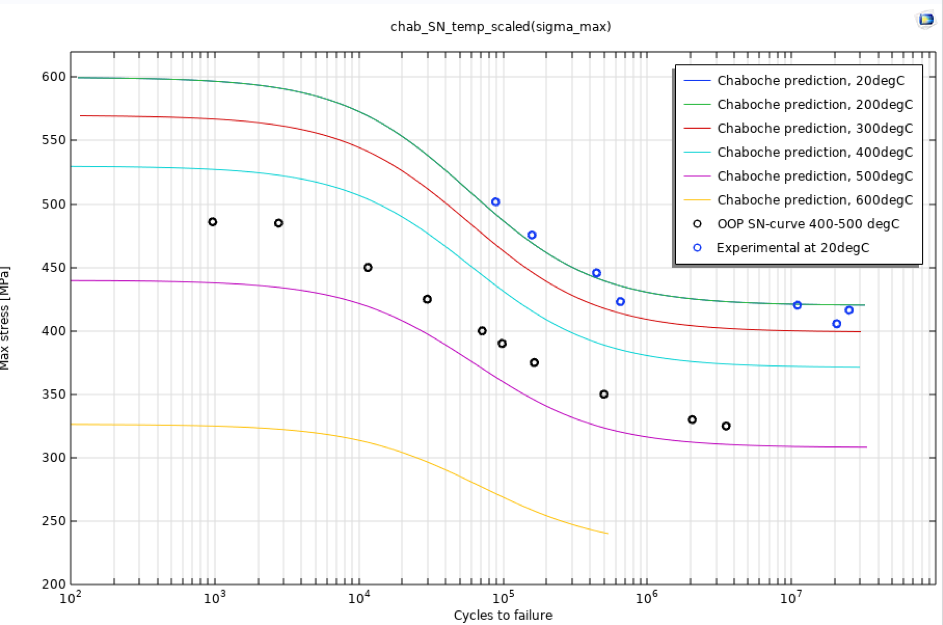
图2 降温后的 Chaboche S-N 曲线。
在下一部分,我们将显示这些温度曲线的缩放实现。还包括由参考文献 2 设置定义的,假定异相温度在 400°C 和 500°C 之间循环,对于选定数量的应力水平计算疲劳失效周期。。
当需要考虑平均应力效应时,参数 b_{fat} 是必需的。必要时,使用相对于平均应力的 Goodman 疲劳极限降低法,即当 \bar\sigma=\sigma_u, \sigma_l=0 时。可以得到 b_{fat}=0.0041/ MPa。
计算模型
背景:实验比较
参考文献 2 中进行了热机械疲劳测试(等温和异相)。单轴拉伸实验在高温下进行,包括等温和非等温条件。为了演示定义热机械疲劳分析所需步骤的过程,在 COMSOL Multiphysics 中复现了实验设置和测试程序,并将已发表的实验结果与分析结果进行比较。
背景:疲劳评估
为了展示比试样更真实的情况,对承受循环温度和压力载荷的压力容器进行了疲劳分析。由此产生应力状态定义了疲劳计算的输入,并估计了失效循环次数。
几何模型:实验比较
参考文献 2中 显示了样品的几何形状。对于循环应力-应变曲线的简单计算,仅将狭窄区域的一半进行轴对称建模就足够了;详请参见图3。请注意,偏离轴向是由于样品上有一个孔。
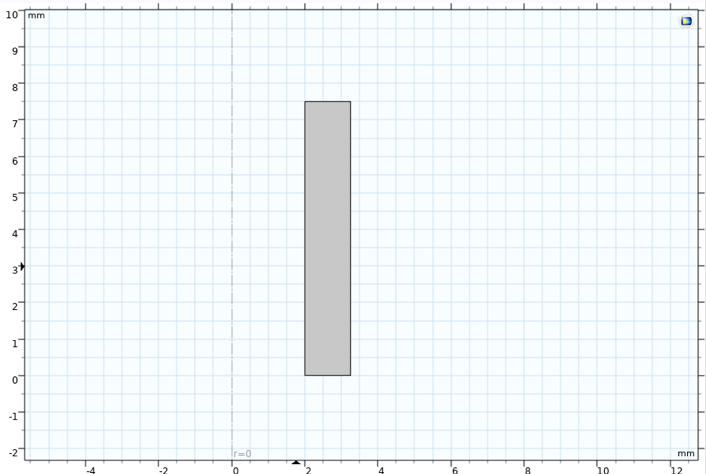
图 3 试样的轴对称模型。
几何模型:疲劳评估
代表热机械疲劳真实情况的压力容器,总长度为6000毫米,内径为950毫米,厚度为50毫米。这可以很容易地将它模拟为轴对称模型,参见图4。
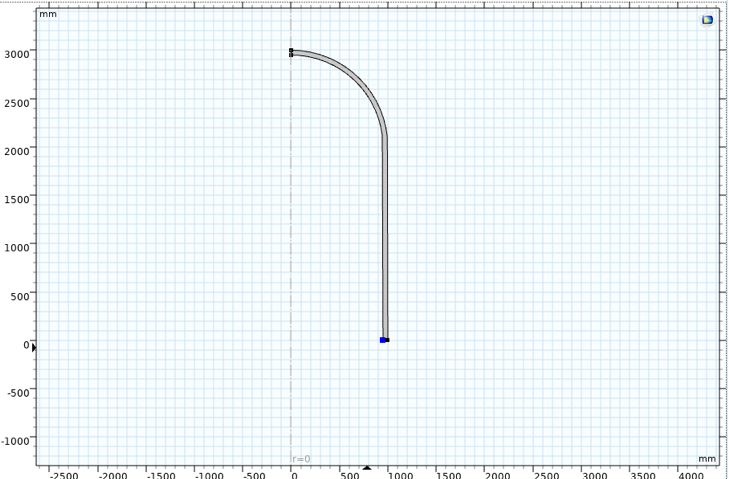
图4 轴对称压力容器模型。
网格:实验比较
在非常均匀的载荷下,网格可以非常粗糙。在这里,它被设置为自由三角形网格,最大单元大小为 0.75mm,如图 5 所示。
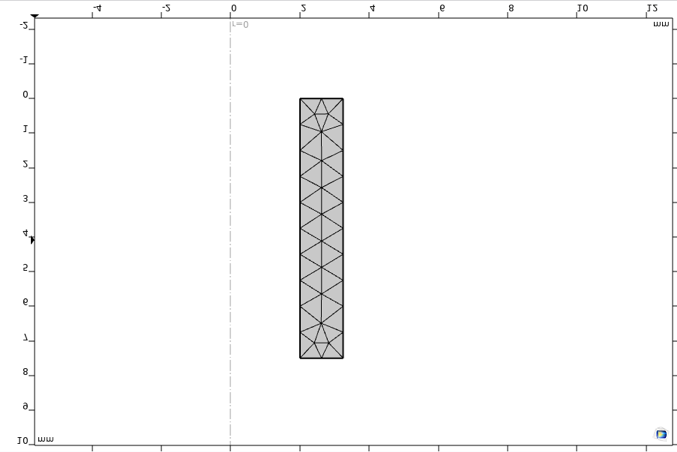
图5 单轴试样网格。
网格:疲劳评估
压力容器模型采用自由三角形网格划分,最大网格尺寸为50 mm,如图6所示。要确保厚度方向上始终存在一个以上的单元,在本篇博文中,出于演示目的,这点并不重要。
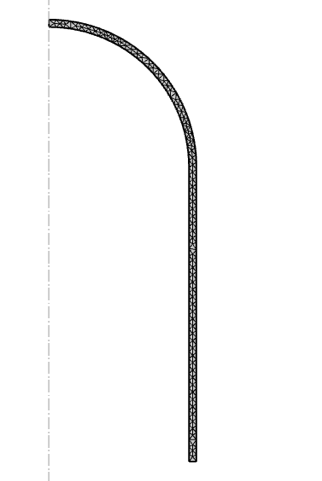
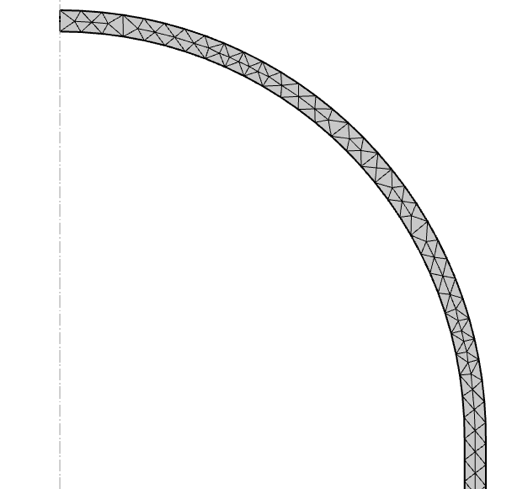
图6 压力容器的网格。
物理场设置:材料、载荷和边界条件(实验比较)
在 COMSOL 中,固体力学 接口用于热机械疲劳分析。首先,必须定义材料。为了实现上一节中描述的模型,我们添加了黏塑性和蠕变的节点,如图7所示。
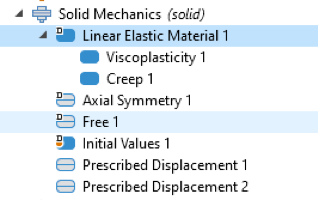
图7 材料定义的必要节点。
对于线性弹性、黏塑性和蠕变节点,适当的材料参数以与温度相关的形式输入,下一节我们将对此进行演示。
由于模型是轴对称的,因此只需要轴向约束。在 z=0 处,底部边界在 z 方向上受到约束。然而,顶部边界被指定为相应载荷工况下测得的应变位移。
物理场设置:材料、载荷、边界条件(疲劳评估)
对于压力容器,材料设置是相同的。同样,对称边在 z=0 处在 z 方向上受到约束。对内壁边界施加压力。该压力载荷为 R=0 负载情况,最大压力为 170bar。温度循环的温度高于实验对比的温度,最高温度(600°C)在 0bar 时,最低温度(500°C)在 170bar 时,加载速率为 5.67bar/s。
研究设置:实验比较
利用蠕变和黏塑性材料模型进行时间相关的研究是必要的。
在等温测试中,初始循环用于比较。应变率为 0.1%/秒时,初始循环时间为20秒。输出时间选择为 2.5 秒。时间步长手动设置为 0.25 秒。
对于非等温情况,使用第50次循环用于实验对比。应变速率为 0.033 %/s,初始循环时间为 60s,总时间为 3000s。输出时间选择在 2.5s,时间步长设置为 1s。温度速率为 3.33℃/s。
研究设置:疲劳评估
对于压力容器分析,载荷和温度速率与非等温实验比较相同。输出和时间步长设置也相同。
定义函数和变量
建立一个适合热机械疲劳分析的模型本身并不一定很复杂,但是上述框架包含很多方面。首先,有必要为温度和与温度相关的材料参数以及载荷的一致变化建立一个框架。在 COMSOL Multiphysics 中,通过使用函数和变量可以方便地进行处理。在本节中,将使用非等温分析(用于实验比较)概述这个方法。
参数
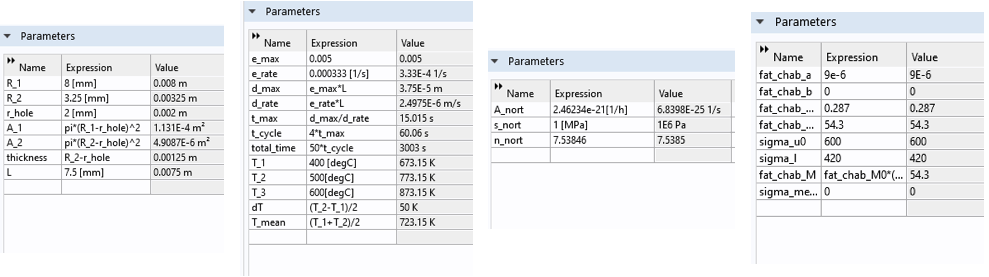
我们首先定义不受解决方案影响的全局参数,包括几何形状、载荷、材料蠕变和材料疲劳参数(见图8)。
现在,标称载荷值(如温度和位移)可以通过简单的比例函数来确定载荷。
温度函数
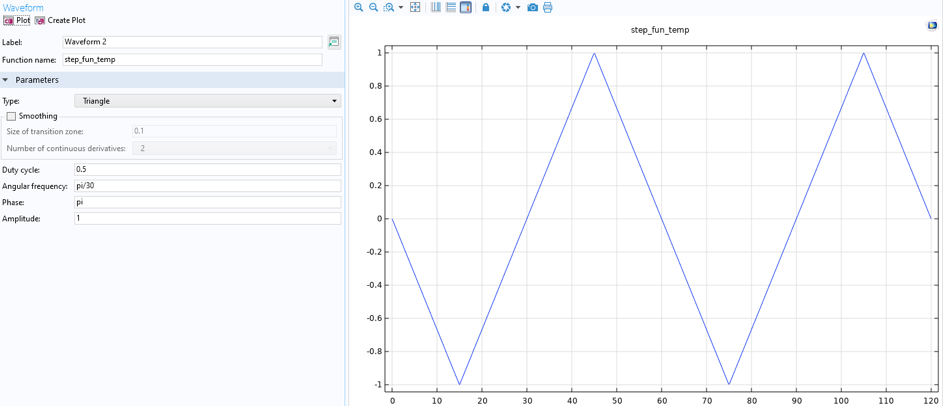
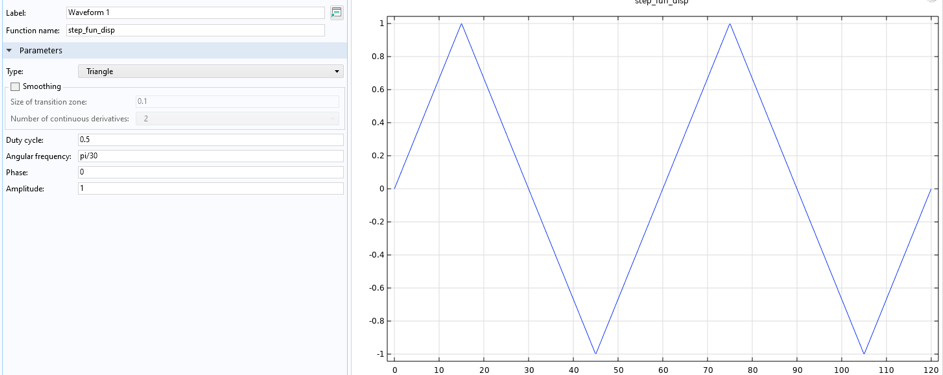
在等温实验中,温度恒定在 400°C。非等温实验要求温度定义为最小应变时的最高温度(500°C),最大应变时的最低温度(400°C)。这种变化是通过创建波形和解析函数获得的,见图9。
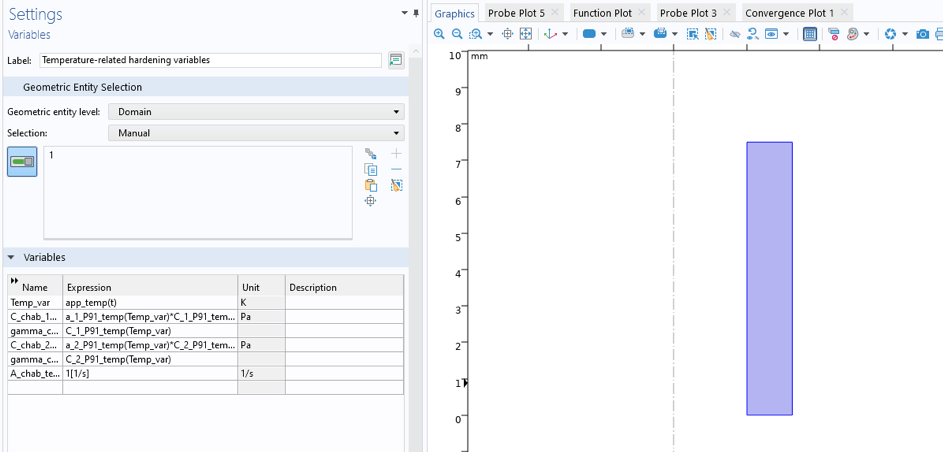
然后,将温度作为变量(TempVar)应用于模型域,见图10。
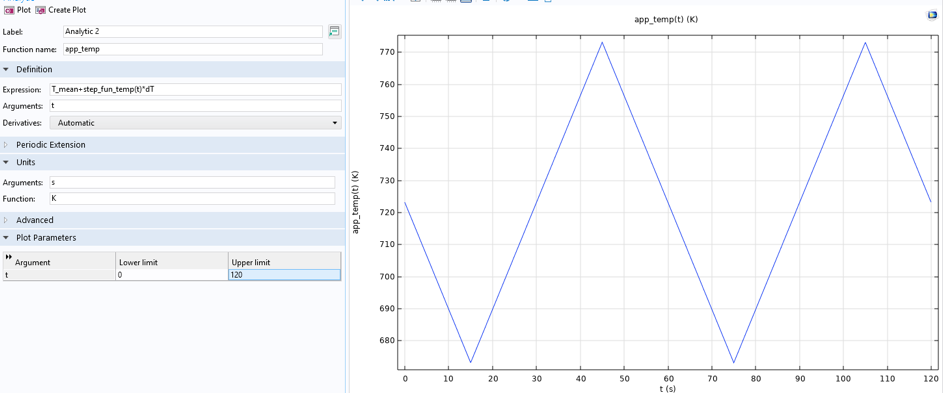
对于压力容器,温度在 500°C 和 600°C 之间循环,如图 11 所示。温度在模型中同样表示为域变量。
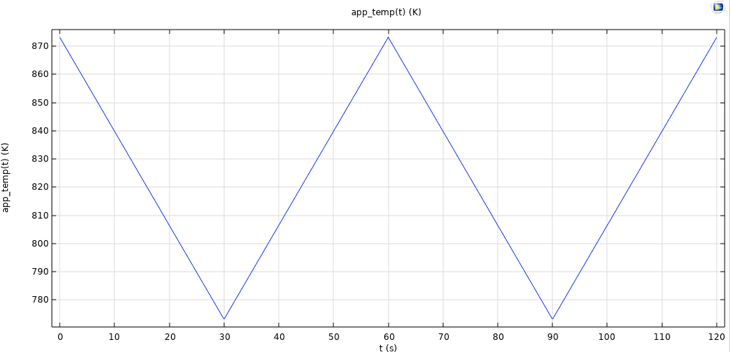
图11 温度函数,压力容器案例。
引入的温度变量可用于确定材料特性的变化,但不考虑热膨胀。由于总应变(机械应变和热应变)是由机器控制的,因此在实验情况下这并不重要,但通常应考虑由于热膨胀引起的热应变。为此,可以添加 固体传热 物理场接口,并添加逐点约束以根据需要强制执行温度,参见图 12。
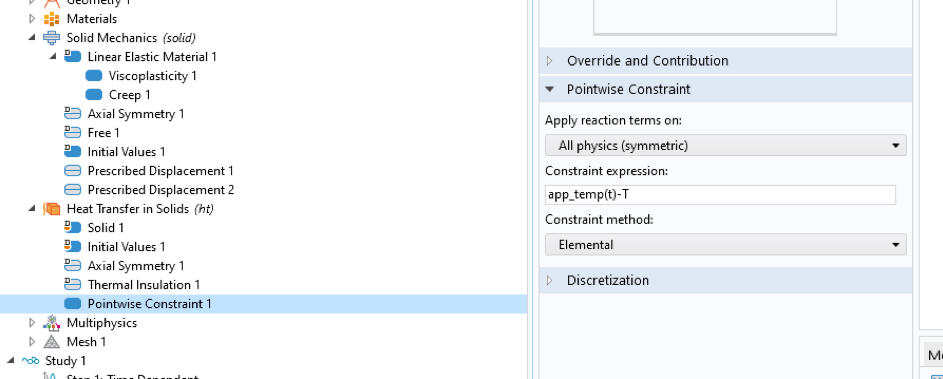
图12 固体传热物理场接口。
当然,均匀的温度分布在现实中是很少的。适当的传热分析也可用于获得温度场。必须为传热分析指定参考温度,即热应变为零的温度,也就是(热)无应力配置。虽然通常这是在室温下进行,但对于疲劳分析来说,通常重要的是温度载荷范围和平均值。因此,在分析中,将参考温度被设置为 873K,即循环的最高温度。
载荷函数
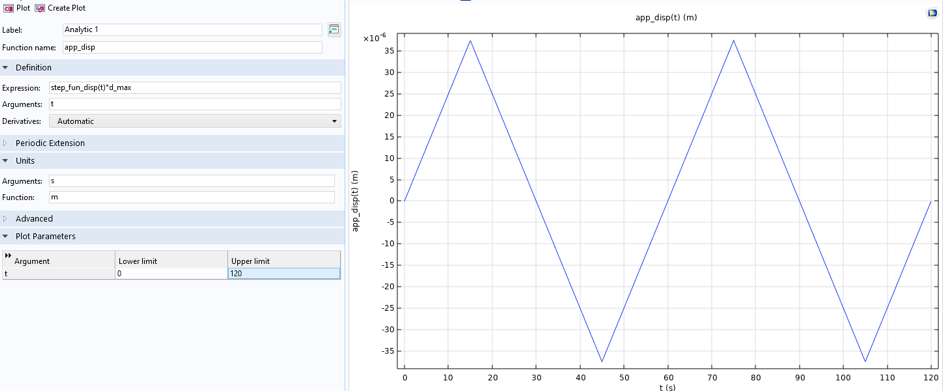
与温度定义类似,载荷(在此实验情况下为位移)也由两个单独的函数定义:波形函数和解析函数(见图 13)。
这个特殊的数字是特定的非等温实验情况。在等温和非等温情况下,应变率不同。后者应变速率为 0.1%/s,前者为 0.033%/s,分别对应于 7.5µm/s 和 2.5µm/s 的位移速率。循环过程中的最大应变为 0.5%,这表示总位移为 37.5µm。这与在测量样品的狭窄区域(7.5mm)上的标距测量应变有关。注意,这里使用的是半长度模型。狭窄区域的全长为 15mm。
在压力容器的情况下,定义了峰值压力为 170bar,载荷率为 5.67bar/s 的载荷函数,如图 14 所示。
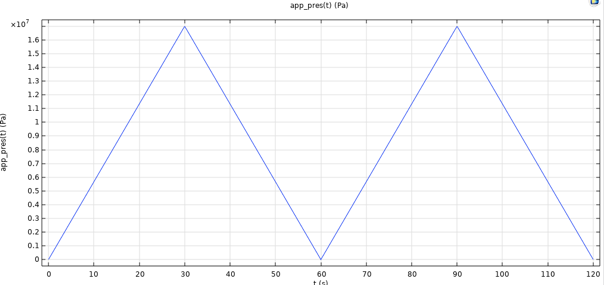
图14 载荷函数,压力容器案例。
材料参数函数
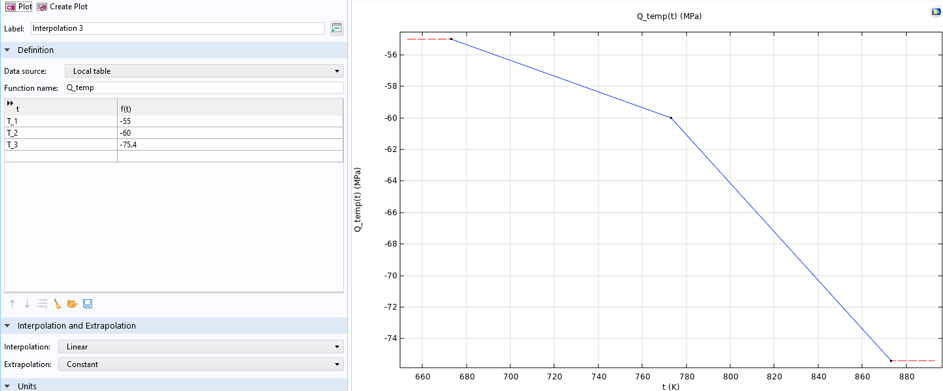
材料参数必须与温度有关,这可以通过在指定温度下用已知参数值创建插值函数轻松获得。例如,图15中被定义的 σsat。
然后,使用创建的温度变量作为参数,通过调用此函数来正确计算与温度相关的材料参数。上述参数见图16所示,参照图9。固体传热 物理场接口的因变量T也可以作为参数。
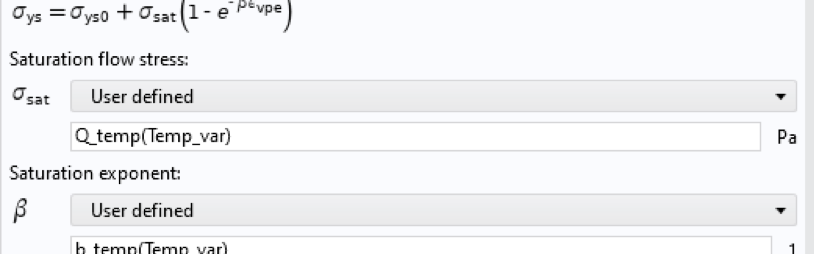
图16 在材料参数定义中调用温度变量。
极限抗拉强度和疲劳极限随温度变化的程序与上述程序相似,尽管室温下的参考值随后用无量纲折减系数进行换算(因为极限强度和疲劳强度都要换算)。图 17 显示了定义 Chaboche S-N 曲线的解析函数表达式(见图 1 和图 2),此处定义为室温(293K)下最大应力的函数。
比例函数 UTS_temp_scaling 的定义如图18所示。
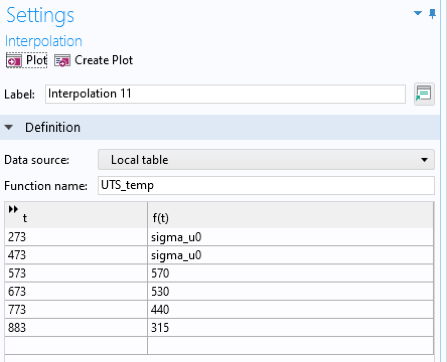
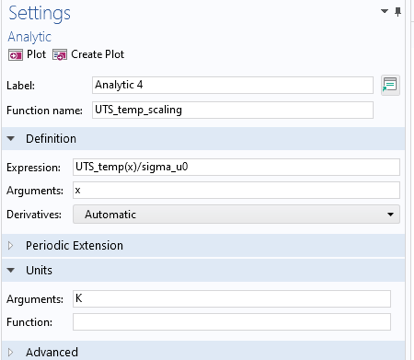
图18 极限拉伸强度的比例函数。
结果:实验比较
在模型的顶部创建了一个第一 Piola–Kirchhoff 应力平均值的边界探针,在此指定了位移。将其提取并绘制为所施加应变的函数,以获得循环应力-应变曲线。
等温测试
初始循环应力-应变曲线如图 19 所示。
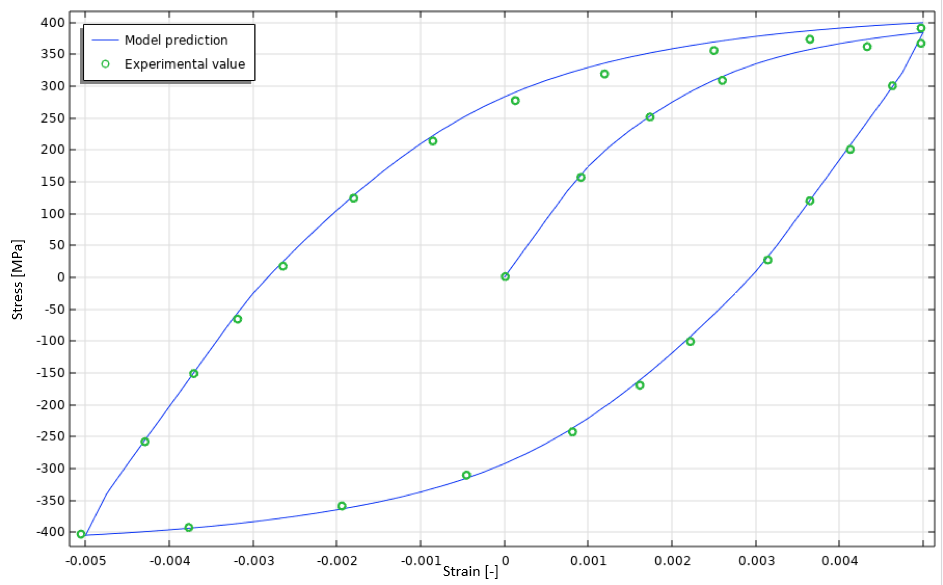
正如预期的那样,这个模型似乎可以很好地预测初始循环应力-应变曲线。
非等温测试
非等温循环应力-应变曲线如图20所示。
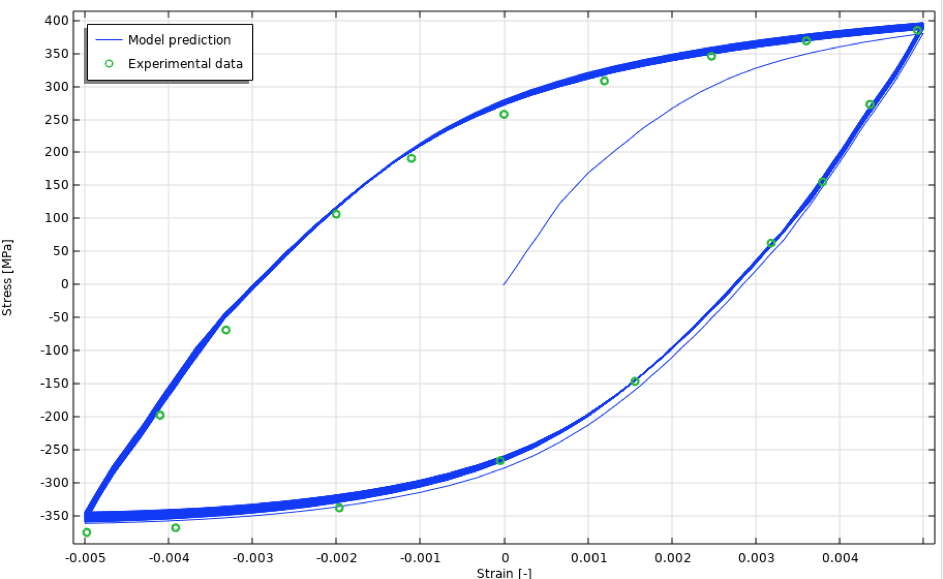
图20 循环应力-应变曲线,等温情况。
独立的第 50 个循环应力-应变曲线,如图 21 所示。
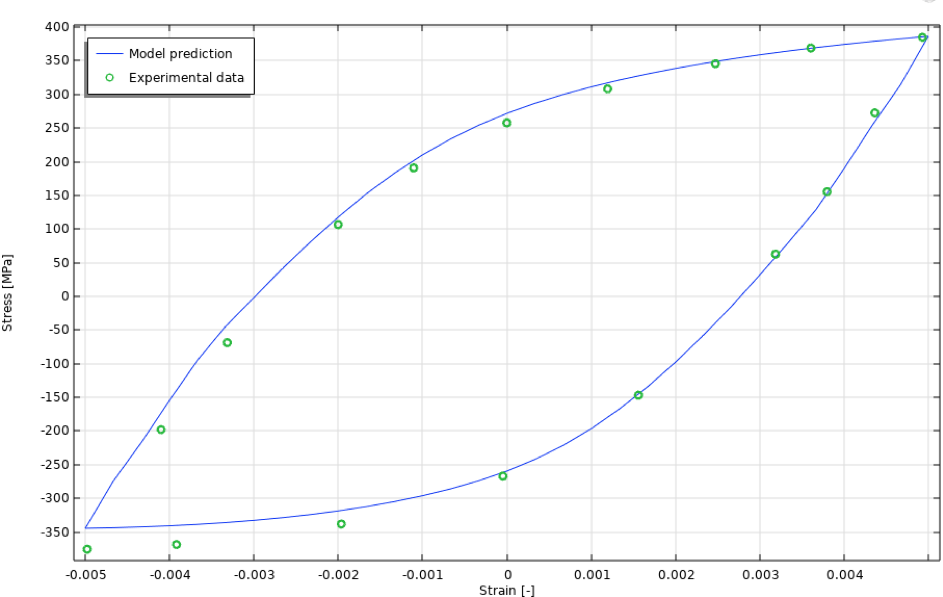
图21 第50次循环应力–应变曲线,等温情况。
结果:疲劳评估
应力和应变
第 50 次循环的最大载荷(2970s)和卸载后(3000s)von Mises 应力如图 22 所示。
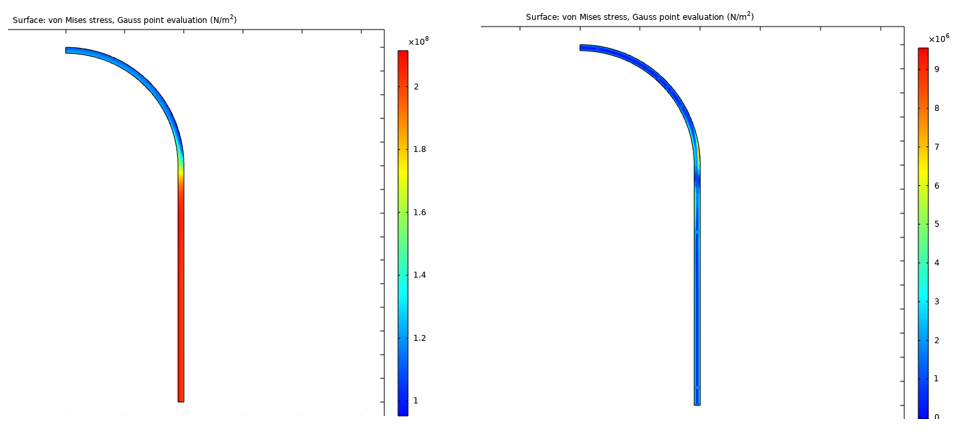
图22 第 50 次循环的最大载荷(2970s)和卸载后(3000s)von Mises 应力
50 次循环后的等效黏塑性和蠕变应变如图 23 所示。
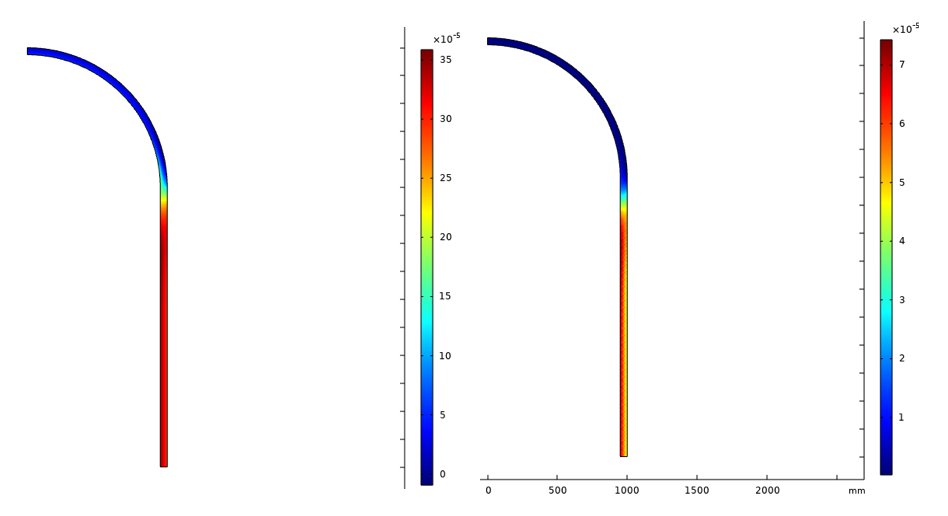
图23 50次循环后的等效黏塑性和蠕变应变。
不对称应力循环的一个典型行为是棘轮效应,其中每个循环的残余应变都会增加。非线性运动硬化模型解释了这一点。通常,随着时间的推移,具有高平均应力的加载循环增加棘轮应变,而较低的平均应力加载循环会稳定棘轮应变。为了估算疲劳循环的次数而不需要计算每个循环直到失效(见下一节),有必要获得一个稳定的应力-应变循环。绘制压力容器中最大等效偏应变的最大von Mises应力,图24显示了两种极端情况下的棘轮应变。
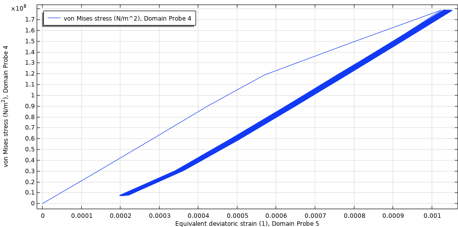
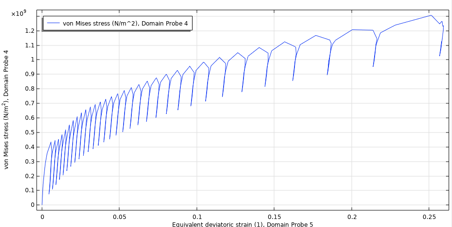
图24 低平均应力-最大压力 100bar (左)和高平均应力-最大压力 240bar(右)的棘轮应变。两种情况都是 R=0 加载。
对于低平均应力,循环周期几乎立即稳定;对于高平均应力,棘轮应变随循环次数的增加而增加。在这里考虑的负载情况下,最大压力为 170bar,前 50 个周期的棘轮效应如图 25 所示,摘自模型右下角。保守地说,也可以提取最大域值。
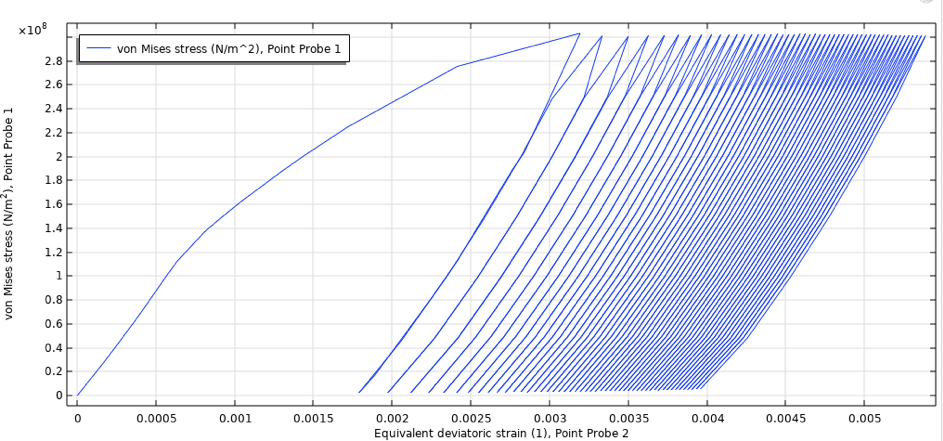
图25 压力容器的应力应变特性,最大压力为 170bar,在 500°C 至 600°C 之间异相循环。
每个循环的棘轮应变都有明显的下降,并且应力-应变曲线可以认为在 50 个循环后趋于稳定。
计算疲劳周期
有几种方法可以使用前面几节中定义的方程来估算部件的疲劳寿命。要计算每个周期的累积损伤,可以先通过找到满足下式的有效温度 T *
然后,可以根据下面的公式计算一个周期的损坏级数:
接着,通过对每个周期的损伤进行求和,得到总损伤。如果这些是有代表性的载荷循环,那么可以获得这种失效序列的次数(D= 1)。也可以简单地计算每个周期的损坏并求和,运行分析直到D= 1。这些方法可能很麻烦,因为它们需要一个框架来定义和评估为每个周期计算的变量。此外,分析一个部件直到失效通常需要几百到几千个计算周期,即使是低周疲劳也是如此。对于大型模型,这通常是不可行的。
然而,如果部件经受单一类型的载荷/温度循环,如本博文中的示例,那么失效的循环次数可以通过以下公式进行分析计算
然后只需计算稳定循环的平均和最大应力,并计算上述表达式。首先,疲劳风险点的应力-应变图应随时间可视化,以确保循环温度。根据图 25,应力-应变循环似乎是稳定的。
根据图 26:149.7MPa,通过最大应力点探针的时间平均算子的派生值来计算平均应力。
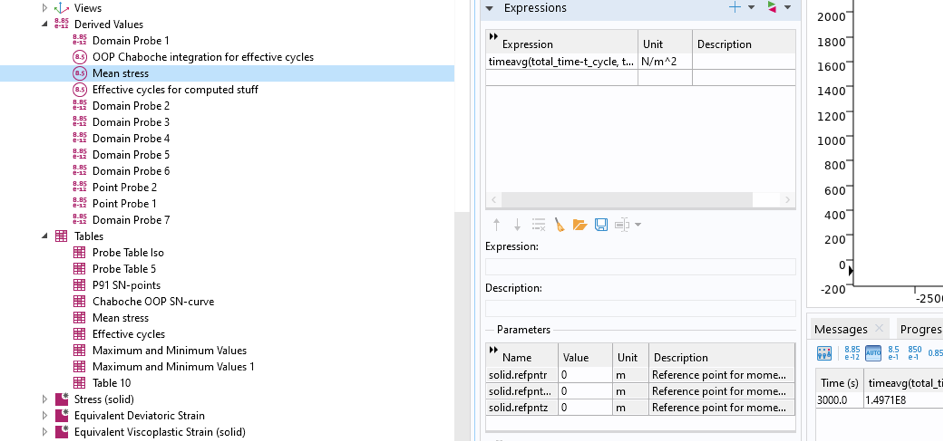
图26 稳定循环的平均应力的计算。
根据图27,循环数的解析表达式 被定义为时间、最大应力和平均应力的函数。该表达式与图17 中的通用表达式不同,因为它必须用于时间积分。

图27 根据时间、最大应力和平均应力计算的失效循环次数的定义。
如图28 所示,它可作为派升值,用于计算失效循环次数。最大应力可以从探针表中很容易获得:313MPa。
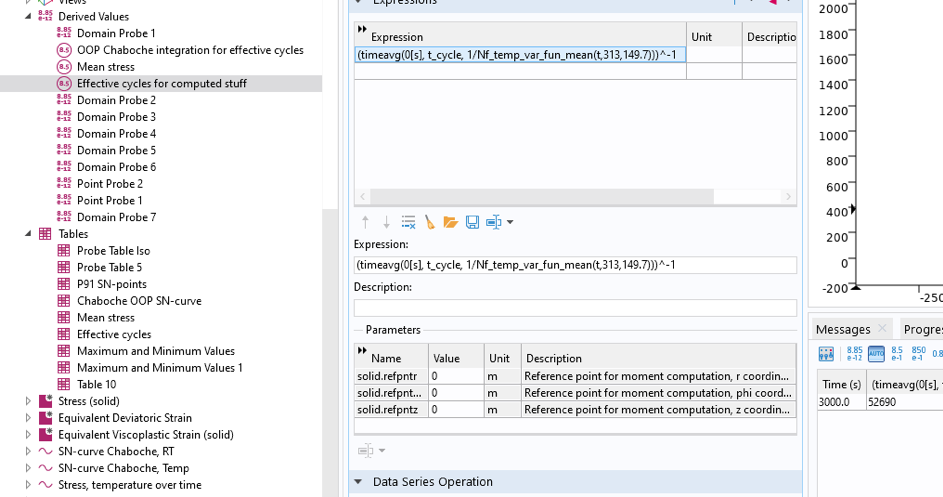
图28 使用 全局评估 节点计算失效的循环数。
计算得出的失效循环次数为 52,690。
结论与讨论
在许多应用中,热机械疲劳至关重要。在更高的温度下运行以减少排放的发电厂只是其中的一个例子。在高温和高载荷下,与温度相关的材料特性、蠕变和热应变都会影响热机械疲劳。
这些现象可以通过使用本文中描述的非线性材料模型在 COMSOL Multiphysics 软件中进行整合。尤其重要的是硬化参数,它控制着循环应力-应变曲线随时间的变化。使用定义温度函数并使材料性能与温度相关,从而可以使用众所周知的 Chaboche 疲劳模型来估计同时承受热载荷和机械载荷的部件的疲劳失效循环次数。如果载荷/温度循环在整个部件寿命期间是相同的,则使用解析表达式很容易做到这一点。
对于更复杂的加载历史,有必要为每个循环找到一个代表该循环中热载荷和机械载荷的有效温度。然后,将它用来适当地调整函数总使用的相关材料参数(在这篇博文中,是极限抗拉强度和疲劳寿命),并计算这个特定循环的损伤。这个增量的过程会积累损伤,当 D=1 时,假设发生疲劳失效。对于任何最高循环周期数超过几千个周期的情况,这都不是一个可行的方法,因为需要的时间太多了。如果可能的话,确定一系列有代表性的循环(负载块)将是更好的方法。
应该注意的一些方面。参考文献中的材料模型使用统一的 Chaboche 黏塑性模型,其中黏性应力被添加到解中,具体取决于 Chaboche 黏塑性硬化模型中使用的相同材料参数。COMSOL Multiphysics 中没有实现统一的黏塑性模型,而在这篇博文中使用了 Norton 蠕变定律。COMSOL Multiphysics 的计算结果与实验数据吻合良好。此外,考虑到 von Mises 应力与静水载荷无关,因此将 von Mises 应力作为疲劳应力使用在技术上可能不是一个好的选择。例如,Sines 准则可能更合适,因为载荷是成比例的,主应力方向可以假设为常数。然而,这篇博文在实现 Sines 标准几乎没有什么收获。
关于作者
Björn Fallqvist 是Lightness by Design 公司的顾问,负责基于数值分析的产品开发。他于 2016 年在皇家理工学院获得博士学位,致力于开发结构模型以捕获生物细胞的机械行为。他的主要专业兴趣和专业领域是材料表征以及使用各种材料模型捕获物理现象。
参考文献
- S. Natesan et al., Preliminary Materials Selection Issues for. s.l. : Argonne National Laboratory, 2006.
- C.J. Hyde et al., “Thermo-mechanical fatigue testing and simulation using a viscoplasticity model for a P91 steel”, Computational materials science, no. 56, 2012.
- J.L. Chaboche and P.M. Lesne, “A non-linear continuous fatigue damage model”, Fatigue fracture and Engineering Materials Structures, vol. 11, no. 1, pp. 1&ndash17, 1987.
- A.A. Saad et al., “Thermal-mechanical fatigue simulation of a P91 steel in a temperature range of 400-600C”, Materials at high temperatures, no. 28, 2011.
- COMSOL Multiphysics, Structural Mechanics Module User’s Guide.
- X. Feng et al., “Determination of creep properties of P91 by small punch testing”, Materials at high temperatures, vol. 32, no. 4, 2015.
- Y. Gorash and D. MacKenzie, Open Eng, vol. 7, 2017.




评论 (6)
康 黄
2021-06-23有这方面的案例吗?包括建模步骤
hao huang
2021-10-08 COMSOL 员工您好,本篇博客暂时还没有相关案例,您可以参考官网其他案例:http://cn.comsol.com/models?q=%E7%83%AD%E7%96%B2%E5%8A%B3
齐叠 林
2021-07-28一楼请求+1
hao huang
2021-10-08 COMSOL 员工您好,本篇博客暂时还没有相关案例,您可以参考官网其他案例:http://cn.comsol.com/models?q=%E7%83%AD%E7%96%B2%E5%8A%B3
pentung wong
2021-09-28有模型文件吗
hao huang
2021-10-08 COMSOL 员工您好,本篇博客暂时还没有相关案例,您可以参考官网其他案例:http://cn.comsol.com/models?q=%E7%83%AD%E7%96%B2%E5%8A%B3