使用 COMSOL Multiphysics® 优化 PID 控制器性能

想象一下，你正在公路旅行，以每小时 60 英里的速度在公路上行驶。为了保持这个速度，你决定打开巡航控制。毕竟你正在度假——为什么不让汽车替你干活呢？无论你是上坡还是下坡，汽车都会对速度变化做出反应，自动加速或减速。这种过程控制归功于比例-积分-微分（PID）控制器。通过仿真，工程技术人员可以优化这种控制装置。

导航过程控制

将速度、温度、流速、压力等变量考虑在内的情况下，过程工程技术人员可以使用自动连续控制来调节系统。过程控制其实就是一致性，通过控制系统或装置来管理各种复杂的过程。自动过程控制的早期形式是离心调速器，它使用旋转砝码来实现风车等系统的平衡。很久以后，人们在蒸汽机中实施了一种形式的调速器，并且应用摆式调速器来控制速度。

在 20 世纪 20 年代，工程技术人员 Nicolas Minorsky 有了用 PID 作为控制形式的想法。他的灵感来自于观察舵手操纵船只，在强风和波涛汹涌的海面上手动纠正航向。在研究美国战舰上的转向系统时，Minorsky 开始研究一个控制理论的公式，这个公式发展成为我们今天所知的三项 PID 控制。

船舶操纵的手动控制为 PID 理论提供了启示。图片由美国海军提供，位于美国公共领域，通过 Wikimedia Commons 分享。

随着时间的推移，PID 设备经历了多次迭代（技术从气动更新到电子）。PID 控制器是一种基于算法的反馈机制，可连续计算所需设定值（SP）与过程变量（PV）之间的误差。PID 控制器可应用于机械装置，实现系统的自动校正，并使 PV 保持在所需的 SP（比如使行驶中的汽车保持一定的速度）。

气动控制器，顶部带有可调刻度盘，用于调节功率、输入和输出项。图片由 Snip3r 提供，在 CC BY-SA 3.0 许可下使用，通过 Wikimedia Commons 分享。

PID 控制常用于化工领域，帮助工业设施通过调整软件自动一致地调节受控系统。为了在这些领域和其他领域进行更精确的控制，工程技术人员可以使用 COMSOL Multiphysics® 软件将 PID 控制器算法耦合到他们的模型来分析过程。

PID 的 3 个数学术语

比例-积分-微分算法由三个控制项组成，这三个控制项协同工作以获得最佳响应。每个项根据 SP 和 PV 控制信号进行不同的计算。当这三个项一起使用时，设备会产生一个控制信号，实现校正以返回到所需的 SP。

每个 PID 项都是消除误差控制的一个方面，作为对误差的当前、过去和未来的计算：

• 比例：给出与当前误差值成比例的输出。
• 积分：对误差随时间的过去值进行积分以计算 I 因子。为了使误差为零，这部分是必要的，因此几乎总是包括在内。
• 微分：估计未来的误差变化率，以弥补 P 和 I 因子造成的任何超调。这部分通常被关闭，原因是，在实际应用中，它会放大随机干扰的影响，进而对控制器的稳定性产生负面影响。

最常见的是使用 PI 的组合，偶尔使用 PID，少数情况下使用 PD（例如用于控制伺服电机）。P 也可以单独使用。

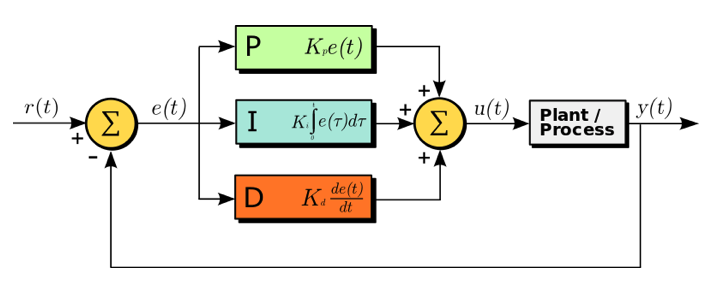
反馈回路中 PID 控制器的示意图，其中 r(t) 是 SP，y(t) 是 PV。图片由 Arturo Urquizo 提供，在 CC BY-SA 3.0 许可下使用，通过 Wikimedia Commons 分享。

由于这三个组件需要在控制系统内同时很好地协同工作，因此很难使 PID 算法中的参数恰好正确。不过，使用 COMSOL Multiphysics，你可以实现一个 PID 控制算法来模拟过程控制系统，从而能够找到最佳控制参数。此外，过程控制机制可以耦合到 COMSOL® 软件中的模型，如下面的流动混合示例所示。

用 PID 装置模拟过程控制

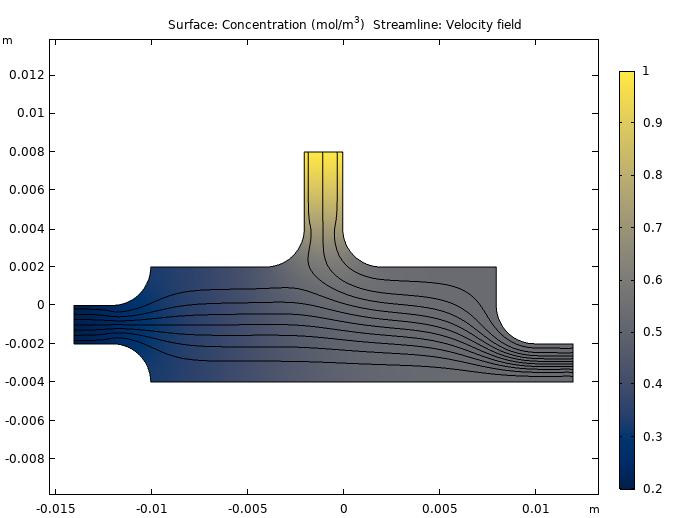
在这个燃烧室模型中，具有两个入口（固定的上部入口和受控的左侧入口）的质量传递和流体流动与 PID 控制器耦合。在腔室内，两股流动混合在一起，每种流动具有不同的氧浓度。其中，用于流量控制的 PV 是腔室中某个测量点处的氧浓度。

PID 控制器用于在测量点处达到 0.5 mol/m³ 的期望浓度（SP）。它通过调节左侧入口的速度、增加或减少氧含量较低的气体流量来实现。氧含量较高的气体以 10 mm/s 的速度从上部入口进入。

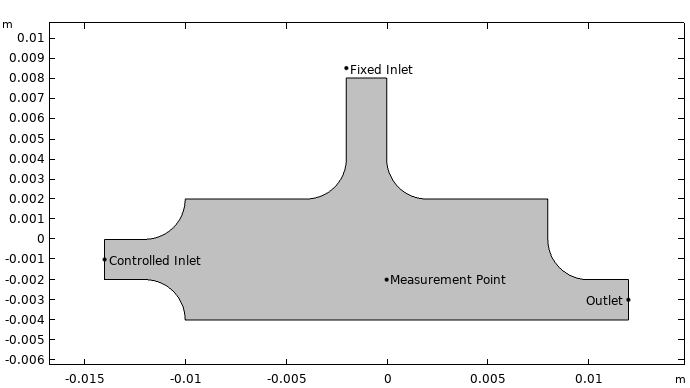
燃烧室的几何结构。

为了分析腔室中的流场，我们使用层流 接口计算流动 的速度和压力。然后，为了计算质量平衡，我们使用稀物质传递 接口，分析了两种流动和化学物质通量发生的对流和扩散。（有关质量传递方程边界条件的详细信息，请参阅模型文档。）

使用域点探针 特征模拟浓度测量。PID 算法由用户定义的变量和全局方程 实现使用以下参数计算 PID 控制的速度：

• c_set — 设定值
• k_p — 比例系数
• k_l — 积分系数
• k_D — 微分系数

对于本例，我们将重点关注改变比例系数（k_p）的效果。

评估仿真结果

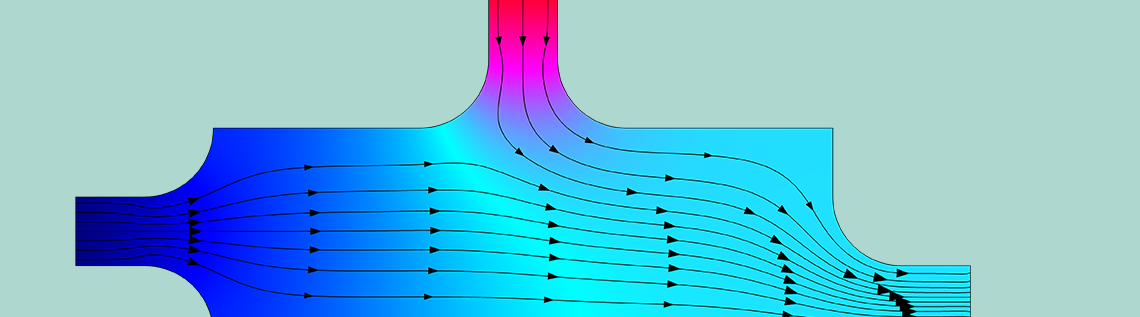
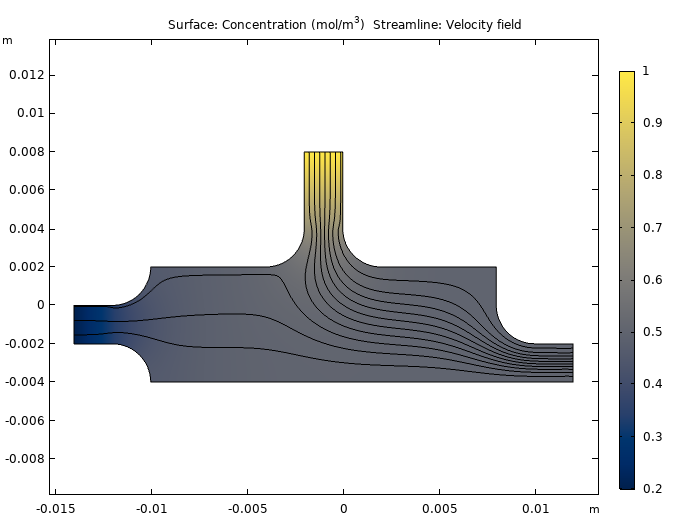
首先，我们看一下 0.1 s（左图）和 1.5 s（右图）后室内速度流线和氧浓度的快照。你可以看到，在早期，进入受控入口的流速度仍然很低，传感器完全暴露在来自顶部入口的高浓度氧气流中。随后，为了降低浓度，控制器增加左侧入口速度。因此，PID 控制器按预期运行，做出改变以保持 SP。结果还表明，正如预期的那样，测得的氧浓度很大程度上取决于流场。

0.1s（左）和 1.5s（右）后燃烧室中的氧浓度（颜色图）和速度场（流线）。

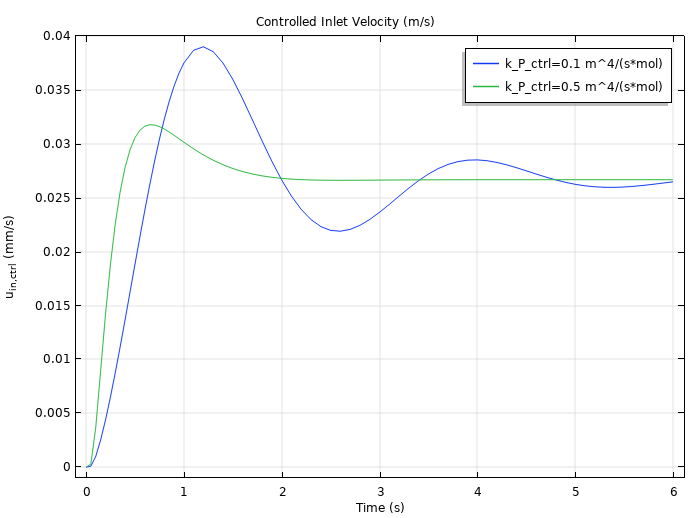
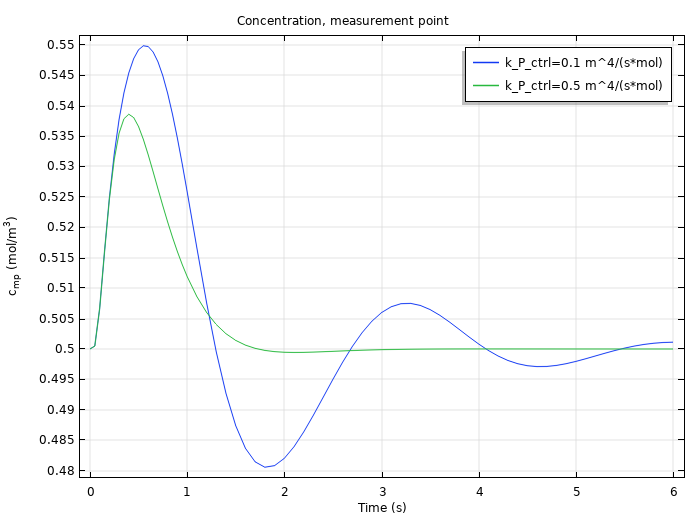
下图显示了选用两个不同的比例参数值 kP = 0.5 m⁴/(mol-s) 和 kP = 0.1 m⁴/(mol-s) ，随时间变化的 PID 控制入口速度（左）和测量点的浓度（右）。在这两个结果中，达到稳态之前，k_p 值较小情况下的结果（蓝色）比 k_p 值较大情况下的结果（绿色）振荡幅度更大。了解这一趋势有助于我们优化 PID 控制算法中的参数。

k_p = 0.5 m⁴/(mol-s)（蓝色）和 kP = 0.1 m⁴/(mol-s)（绿色）情况下，随时间变化的 PID 控制入口速度（左）和测量点的浓度（右） 。

今后，你可以将同样的建模技术应用于其他 PID 项，以便继续改进控制器，以及模拟其他系统的 PID 控制器。

后续操作

单击下面的按钮进入“案例下载”页面，尝试操作 PID 控制器示例，你可以在该页面下载 PDF 文档，并使用有效的软件许可证下载模型 MPH 文件。

阅读此篇博客文章了解有关过程控制的更多信息：使用组件耦合实现简单的温度控制器