最新内容

混合计算:共享内存与分布式内存相结合的优势
在之前的混合计算系列博客中,我的同事 Pär 介绍了如何在共享内存和分布式内存平台上使用 COMSOL Multiphysics 进行并行数值模拟。今天,我将讨论这两种方法的结合:混合计算。

绘制磁场的空间导数
对于放射学、磁电泳、粒子加速器和地球物理学等领域的应用,计算磁场或磁通量密度的空间导数都很有用。
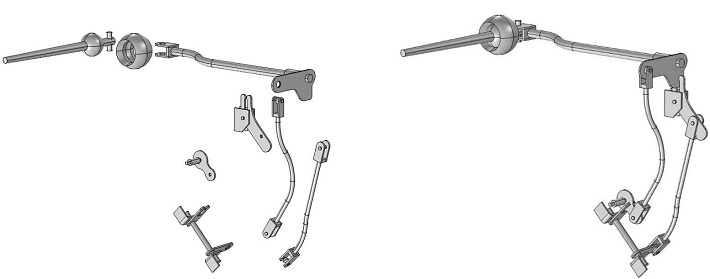
选择第一档:研究老式汽车的换挡原理
跟随我们一起对一辆老爷车的换挡机构进行多体动力学分析。准备上路了吗?
质子交换膜燃料电池建模示例
聚合物电解质膜或质子交换膜(proton exchange membrane,简称 PEM)燃料电池是一种极具应用潜力的便携式清洁电源,是交通运输和发电行业的研究热点。COMSOL Multiphysics,这款强大的仿真工具,可以帮助理解和克服 PEM 电池燃料设计和施工过程中的挑战。

如何在 COMSOL Multiphysics 中模拟热粘性声学
当模拟声学现象、尤其是对几何尺寸非常小的声学装置而言,需要考虑许多复杂因素。热粘性声学 接口为声学模型的建立,及对声压、速度场、温度变化等因素的求解提供了一个简便、精确的方法。在本文中,我们将介绍如何在 COMSOL Multiphysics 中模拟热粘性声学问题,同时还为您提供了一些操作技巧和有用的资源。

热粘性声学的理论基础:热损耗与粘性损耗
当声音在尺寸狭小的建筑和几何结构内传播时,热损耗和粘性损耗会导致声波衰减。具体来说,损耗发生在近壁的声-热边界层与粘性边界层中。为了建立与实验测量结果精确匹配的模型,我们需要考虑这一已知现象,并评估这些损耗对热粘性声学系统造成的影响。

分布式内存计算入门:定义、目的及原理
在“混合建模”系列的上一篇文章中,我们讨论了有关共享内存计算的基础知识:什么是共享内存、为什么使用共享内存,以及 COMSOL 软件如何在计算中利用共享内存。今天,我们将讨论混合并行计算的另一个组成分支:分布式内存计算。
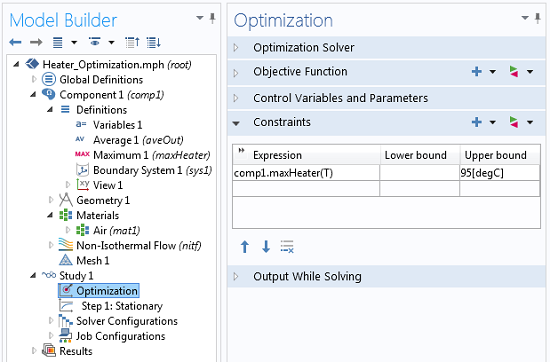
优化加热器功率
我们展示了一种使用 COMSOL Multiphysics® 和优化模块进行过程控制建模和优化的有用方法。
