
在上一篇博客中,我们介绍了线性拉伸算子并演示了如何使用它们在源和目标之间映射变量。如前面所讲的,这种方法仅限于通过仿射变换将源和目标相关联的情况。今天,我们将讨论广义拉伸算子,旨在处理非线性映射和不同维度的几何实体之间的变量映射。
拉伸算子简要回顾
在目标实体中的一点处 P_d,我们希望计算一个量,该量是在源实体中定义的另一个量的函数。因此,来自源点 P_s 的量需要被复制到目标实体。拉伸算子用于识别源实体中的哪一点与目标实体中的某点相对应。换句话说,算子定义了点到点映射。
如果映射是仿射,知道源中的一些点如何对应于目标实体中的点就足够了。从这样的源-目标对中,可以从叠加推断出一般的映射。然而,一般来说,我们需要为映射编写数学表达式。这个表达式可以是源点 P_s 作为 P_d 的函数的显式定义,或者是 P_d 和 P_s 之间的隐式关系。
在 COMSOL Multiphysics 中使用广义拉伸算子
当使用 线性拉伸算子 时,我们直观地指出了足够多的点(基)的映射,COMSOL Multiphysics 计算出了如何转换剩余的点。使用广义拉伸算子 时,我们写出了目标域中任意点映射的数学描述。
首先,我们来重点讨论如何使用广义拉伸算子复制线性拉伸算子。然后,我们可以考虑必须使用一般拉伸算子的示例。
对于仿射关系,广义拉伸算子可以用作线性拉伸算子的替代。当涉及到一般的非线性映射时,广义拉伸算子是必要的。要添加广义拉伸算子,请点击 定义 > 非局部耦合 > 广义拉伸算子。
示例1
在关于线性拉伸算子的博客文章中,我们考虑了一个放射,它将源域中的点 1、4 和 2 与目标域中的点 1、5 和 3 配对。请看下面的图,几何图形中的两个圆的圆心在原点,半径分别为 1.0 和 1.5。
任何仿射变换都可以表示为线性变换和平移运算的和。因此,我们有
现在我们需要找到常数 a,b,c,d,e, 和 f。由于源点(0,0),(1.0, 0)和(0,1.0) 分别对应于目标点(0,0) ,(1.5, 0)和(0,1.5),我们得到
现在我们知道如何找到源点的相应坐标,根据给定目标中的任意点(x,y),我们在广义拉伸设置窗口的目标映射中输入上述等式的右侧(没有下标)。
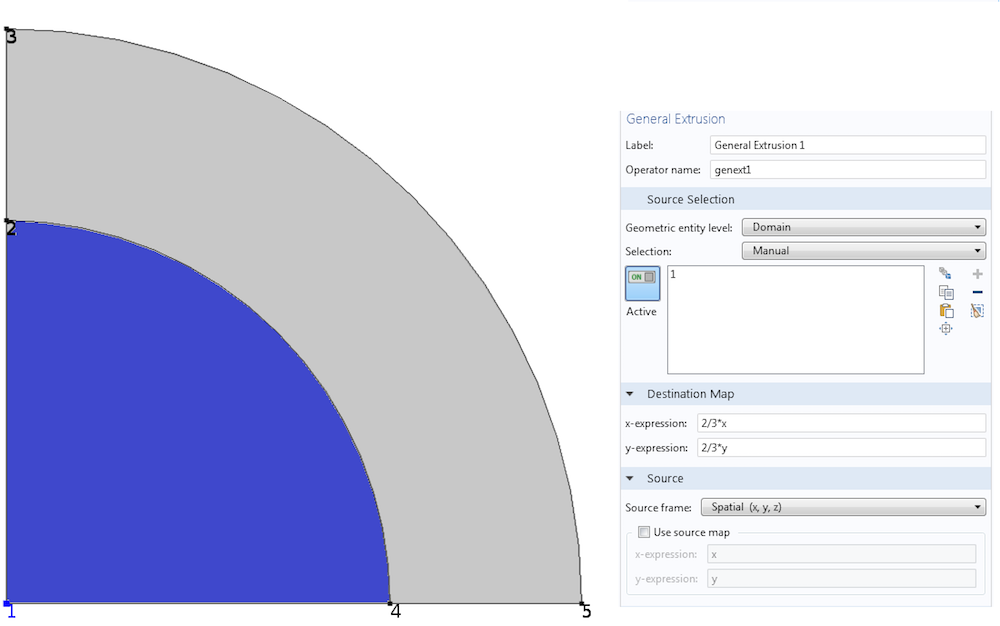
使用广义拉伸算子构建的线性映射。
示例 2
现在,让我们探索如何使用广义拉伸算子将数据从 2D 轴对称组件复制到三维组件,以使源点和目标点对应于空间中的同一点。考虑具有轴对称热边界条件和材料特性的热膨胀。如果结构边界条件不是轴对称的,我们可以通过在一个组件中执行轴对称热分析来节省时间,然后将温度从 2D 轴对称域映射到 3D 域,以便在另一个组件中进行结构分析。
在构建映射时,重要的是提出以下问题: 给定目标点的坐标,我们如何得到源点?在这种情况下,该关系由下式给出
与示例1一样,我们将等号右侧表达式输入目标映射处。
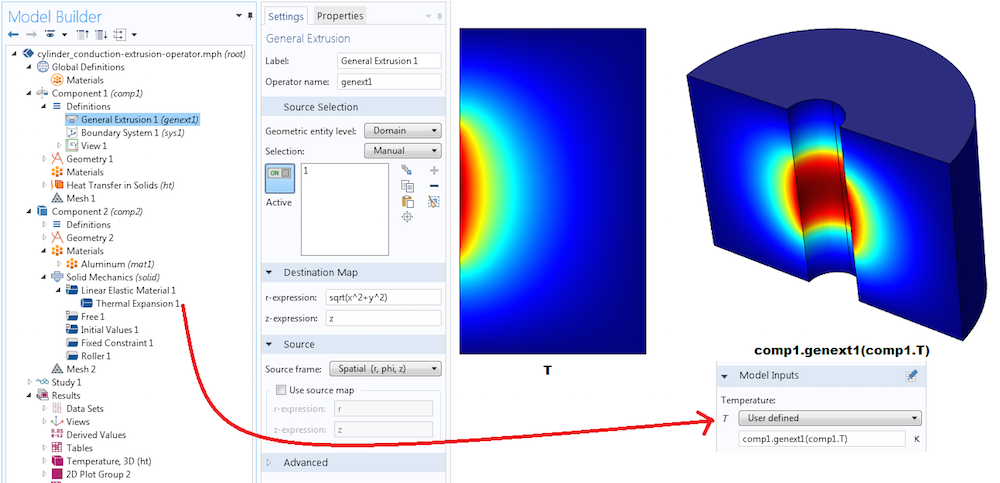
使用广义拉伸算子将数据从 2D 轴对称域复制到相应的 3D 域。请注意,对于轴对称组件,可以在结果节点中使用旋转 2D 数据集以 3D 方式查看变量。然而,如果想在 3D 组件的物理场节点中使用来自 2D 轴对称组件的变量(即热膨胀)<,我们需要使用广义拉伸算子。
算子 genext1 在 3D 组件 comp2 内部未知,T 也未知。如果我们想将 2D 轴对称组件的温度作为 3D 组件的输入,必须使用 comp1.genext1(comp1.T)。如果有一个拉伸或另一个算子(也称为 genext1),或者在第二个组件中也有个叫做 T 的变量时,这个方法将避免出现混乱。
请注意,这里不能使用线性拉伸算子。因为源对象和目标对象具有不同的维度,所以仿射变换是不可能的。
在前两个例子中,“源”中设置窗口中的使用源映射复选框未被选中。COMSOL Multiphysics 在第一种情况下填充和,在第二种情况下填充和。如果不选中此复选框,COMSOL Multiphysics 会假设源的坐标,都有作为目标坐标函数的显式表达式。然而,通常我们可能没有明确的表达式。
接下来,我们将看看如何使用广义拉伸算子来指定隐式关系。
示例 3
2D 抛物线由 \frac{y}{d} =(\frac{ x}{d})^2 给出,它位于边 d 的正方形域内。我们的任务是构建一个算子,将这条曲线(下图中用蓝色表示)的数据映射到正方形的不同部分。抛物线是源。我们想要从抛物线上的一个点复制到正方形中的一个点的算子,例如目标点到原点的距离等于原点和源点之间的抛物线段的长度。
使用一点微积分就可以得到原点和源点 (x,y) 之间抛物线的弧长。
因此,源点和目标点之间的关系是
如果我们想要源-目标的显式映射形式
我们首先需要反转表达式 L=\frac{x_s}{2}\sqrt{1+4(\frac{x_s}{d})^2}+\frac{d}{4}\ln(2\frac{x_s}{d}+\sqrt{1+4(\frac{x_s}{d})^2}),将 x_s 用 L 表示,这一点都不好玩!
这就是为什么 COMSOL Multiphysics 允许我们通过使用两个映射来指定源和目标坐标之间的隐式关系:目标映射和源映射。我们需要提供 T_d 和 T_s ,例如
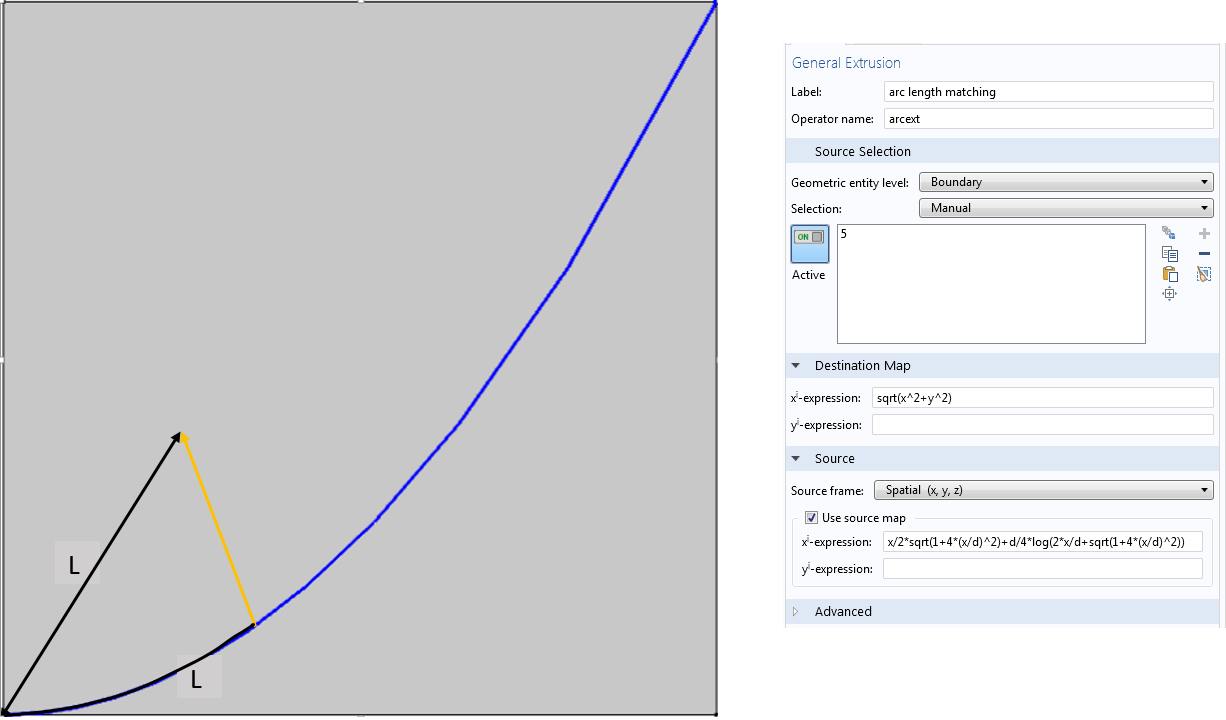
在广义拉伸算子中使用源和目标映射来定义源和目标坐标之间的隐式关系。
COMSOL Multiphysics 会处理 T_s^{-1}(T_d(x_d,y_d)),这是识别源坐标的必要步骤。请注意,源映射需要一对一,这样逆映射才能存在。实际上,COMSOL Multiphysics 并不为源映射逆构造解析表达式。相反,在每个目标点,它首先计算 T_d(x_d,y_d) 并且在源上执行网格搜索操作以找到源上匹配的点 T_s(x_s,y_s)。一对一的源映射使搜索最多返回给定目标点一个源点。
在上面显示的“广义拉伸设置”窗口中,位于目标映射 和 源 下的标签识别为 x^i–表达式和 y^i–表达式 而不是 x– 表达式 和 y–表达式。原因是 x^i 和 y^i 是用于隐式定义源-目标关系的第一对和第二对表达式的指数。它们不一定属于源或目标中 x 或者 y 坐标。从某种意义上说,这些指数是中间网格的坐标,广义拉伸算子匹配具有相同中间坐标的源点和目标点。在这个例子中,一个表达式足够唯一地将正方形域中的任何目的点与抛物线上的源点相关联。因此,第二个线性 y^i– 表达式 为空的。
为了解这种广义拉伸算子是如何映射变量的,考虑一个左右边界分别为 300K 和 400K 温度的平面稳态传热问题。顶面和底面是绝热,没有热源。温度将随线性变化。从下图中,你能看出为什么 arcext(T) 的绘图右边显示了径向变化?
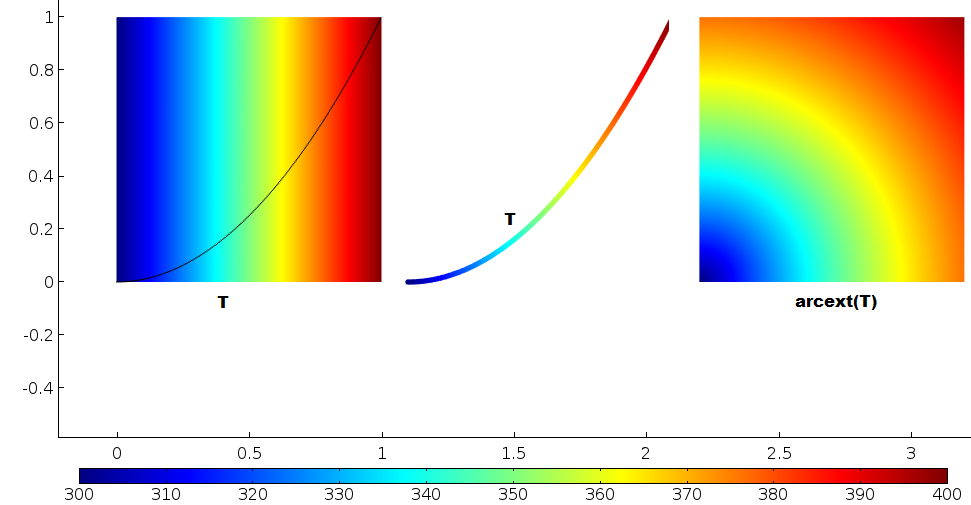
左:温度从左到右呈线性变化。中心:沿抛物线的温度分布。右:温度从抛物线映射到定义域。域中的所有与原点等距点从抛物线上同一点复制温度。
将一切拼凑在一起
为了应用我们前面所学的知识,现在让我们使用 COMSOL Multiphysics 中的电流 物理场接口。拉伸算子帮助我们在理想 p-n 结的每一侧构造法向电流密度边界条件。我们可以将不同的边标记为1和2,如下图所示。结处使用电流-电压关系的 Shockley 二极管方程。参数 J_s, q, k, \textrm{和} T 分别代表下列参数: 饱和电流密度、电荷、玻尔兹曼常数和温度。
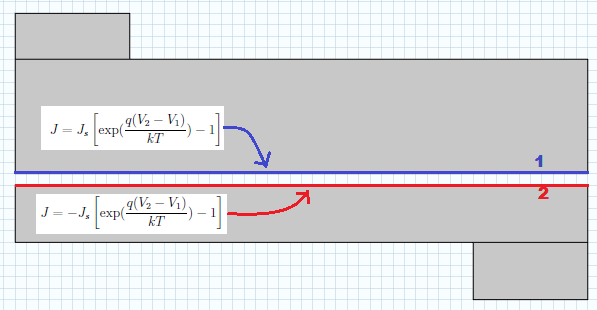
拉伸算子可用于获取结点另一侧的电位。
为了在边界1 侧施加法向电流边界条件,我们需要访问边界2 处的电势。同样,在边界2处 V_2,我们需要访问结另一边的电势 V_1。因此,需要两个拉伸算子。结的每一侧都成为一个拉伸算子中的源实体,如下所示。
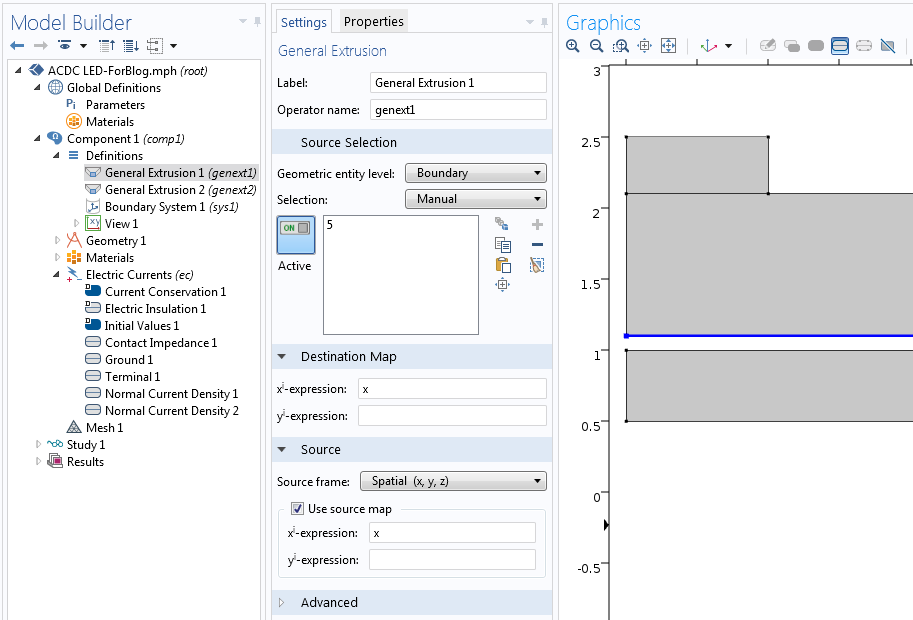
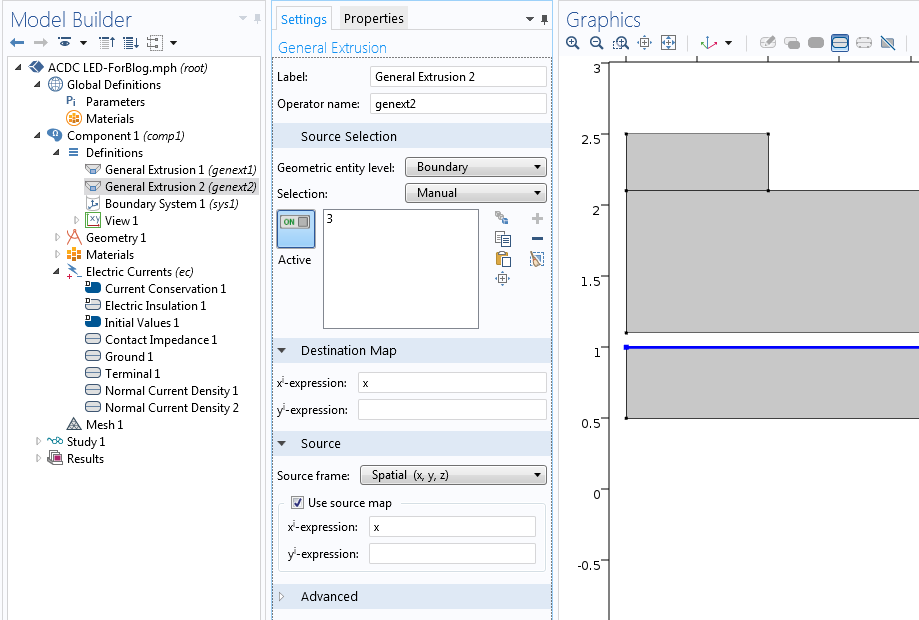
这两种情况都涉及共享同一 x 坐标的两个点之间的映射。因为源实体不同,所以需要两个算子。
现在,我们将使用物理节点中的算子来实现边界条件。顶部的边界条件如下所示。注意,V 指顶部某点的电势,而 genext 2(V) 指底部垂直的电势。
类似的边界条件用于结的底部。相应施加在边3 的法向电流密度 2 节点的法向电流密度是 -Js *(exp((V-gene XT 1(V))/kTbyq)-1)。这里,V 指底部某点的电势,而 genext1(V) 指顶部垂直的电势。
事实上,对电压差使用表达式 genext2(V)-genext1(V) 可以创建一个快捷表达式,而不考虑施加到哪一侧。为了清楚起见,我们这里没有使用这个技巧。
在器件底部有一个电压端,在器件顶部有一个接地端,可以获得以下结果。
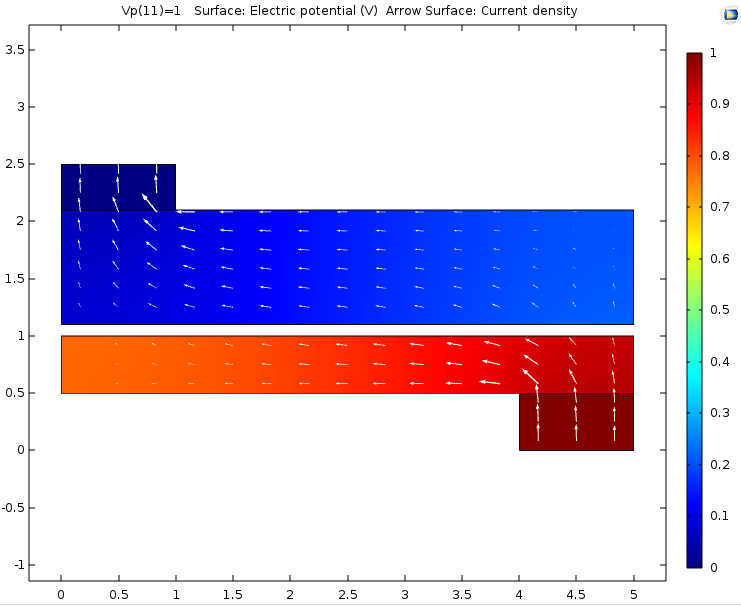
拉伸算子可用于耦合同一组件或不同组件中的点。这里,二极管中的 p-n 结由几何图形中的一个薄间隙表示。为了计算流过间隙的电流密度,通过使用拉伸算子从另一侧获取间隙一侧的电势。
其他组件耦合算子
拉伸算子用于构建源点和目标点之间的逐点关系。有时,我们可能想要访问源线、表面或体积上的积分、平均值、最大值或最小值。在这种情况下,我们可以使用投影、积分、平均、最大或最小分量耦合。您可以在上一篇博文中了解更多关于投影算子的使用。
结束语
今天,我们已经讨论了如何使用广义拉伸算子来创建映射,以便将变量从模拟域的一部分复制到另一部分。除了简单地复制已知的量之外,这些算子还可以用来在未知变量之间创建非局部耦合,如我们的 p-n 结示例所示。这种方法也适用于其他分析,包括结构接触或传热中的表面对表面辐射。COMSOL Multiphysics 包括与这种物理效应相关的内置功能。
如果您想要模拟不包含在 COMSOL Multiphysics 的内置功能中的非局部耦合,您可以使用今天学习的策略来实现它们。如果你有任何问题,请随时联系我们!
拓展阅读
要探索在其他类型的情况下使用广义拉伸算子,请查阅以下博客文章:




评论 (0)