
在过去的七年中,制造业产出共增长了约 10~20%,这部分归功于技术与工艺不断发展,节省了时间和成本,比如 3D 打印技术和本文所描述的粉末压制。在最新版本的 COMSOL Multiphysics® 软件中,我们可以使用全新的多孔塑性模型来模拟该工艺。
粉末压制促进制造行业进步
粉末压制 是指将金属粉末放入模具内,然后施加压力进行压实。模具型腔内的冲压工具(一般位于底面)负责施加高压。金属粉末被压实并塑造成特定的形状后,将从模具型腔中排出。

利用粉末压制技术,金属粉末被制成为固体部件。图像由 Alchemist-hp 提供,已获 CC BY-SA 3.0 DE 许可,通过 Wikimedia Commons 共享。
粉末压制工艺平均每分钟可生产 15~30 个部件,这使得制造商能够快速地设计出坚固的部件。与此同时,部件不需要大量额外处理,所以这套工艺还具有节约成本的优势。
从仿真的角度来看,我们需要对粉末压制进行高度非线性结构分析,借此解释:
- 活动部件之间的接触
- 适用于金属粉末的弹塑性本构定律
- 大位移导致的几何非线性
正如本文将演示的,COMSOL Multiphysics® 5.3 版本是处理此类分析的理想工具。
建模实例:利用粉末压制制造杯子
在本例中,我们考虑利用粉末压制制作一个杯形件。几何模型包含工件(本例中为金属粉末)和模具。需要注意的是,冲压工具不是模型设置的一部分。为了压实粉末,我们在粉末上表面和下表面的法向方向施加指定位移。由于模型呈轴对称,我们将其简化为二维模型,从而减少仿真的计算时间。
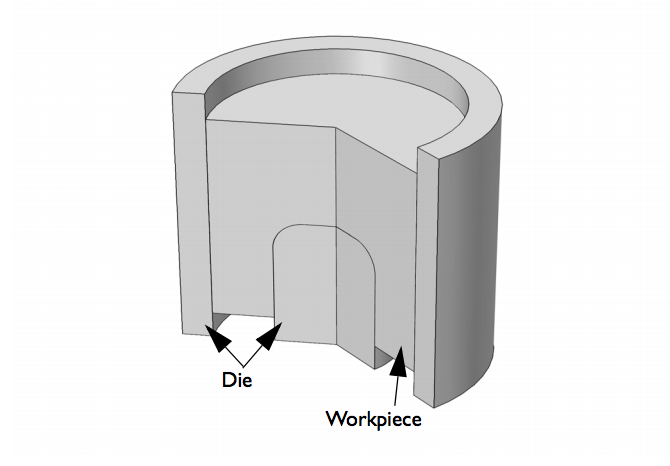
粉末压制分析的几何模型。
最新版本的 COMSOL Multiphysics 包含五种全新的多孔塑性模型,涵盖各种孔隙率值。
- Shima-Oyane
- Gurson
- Gurson-Tvergaard-Needleman
- Fleck-Kuhn-McMeeking
- FKM-GTN
这些模型对于模拟粉末压制而言很重要,因为我们可以借助它们精确地表征工件的孔隙率,并生成可靠的结果。在本例中,我们将 Fleck-Kuhn-McMeeking 和 Gurson-Tvergaard-Needleman 模型相结合,借此描述铝金属粉末。需要注意的是,考虑模具的材料属性,我们假定它为刚性。
除了上文提到的指定位移 边界条件之外,我们还将内部和外部模具设为固定域。
评估 COMSOL Multiphysics® 仿真结果
基于仿真结果,我们可以评估经过压实的金属粉末的各方面特性。首先是体积塑性应变。圆角中心的应变看起来最小,端部的应变较大。工件的拐角点处的应力大约为 12%——可能是与模具摩擦的结果 。
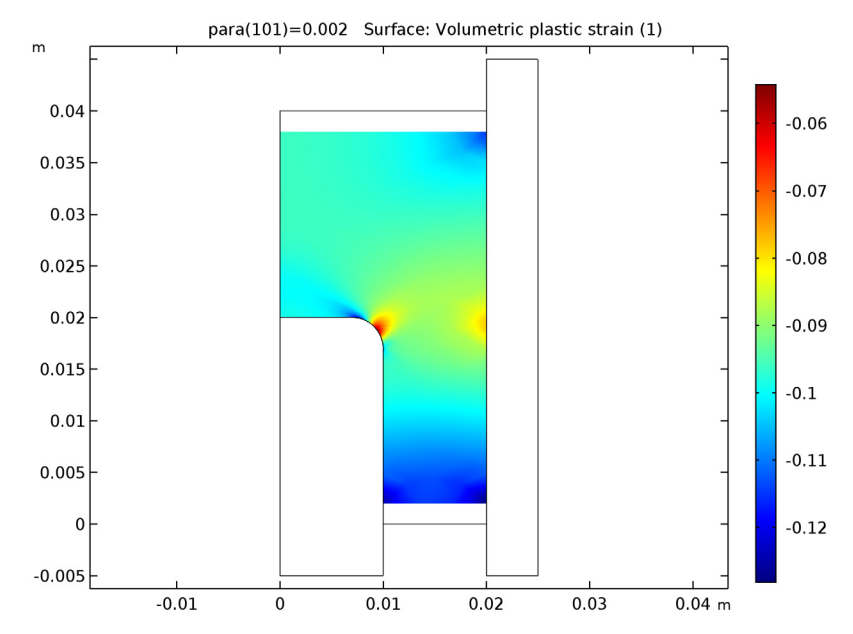
工件在压制过程结束时的体积塑性应变。
在压实过程中,随着部件密度和强度不断增加,铝粉末的孔隙率随之下降。考虑到此例采用的几何结构和负载,我们预测孔隙率的变化将是不均匀的。下方绘图展示了粉末的当前孔隙体积分数等值线;即粉末的孔隙率。与工件的中部和顶部相比,较窄的底部的金属粉末更加紧实。在靠近圆角的中心区域,由于材料在圆角上滑动,因此粉末的紧实度较差。下方动画演示了体积分数随时间的变化。
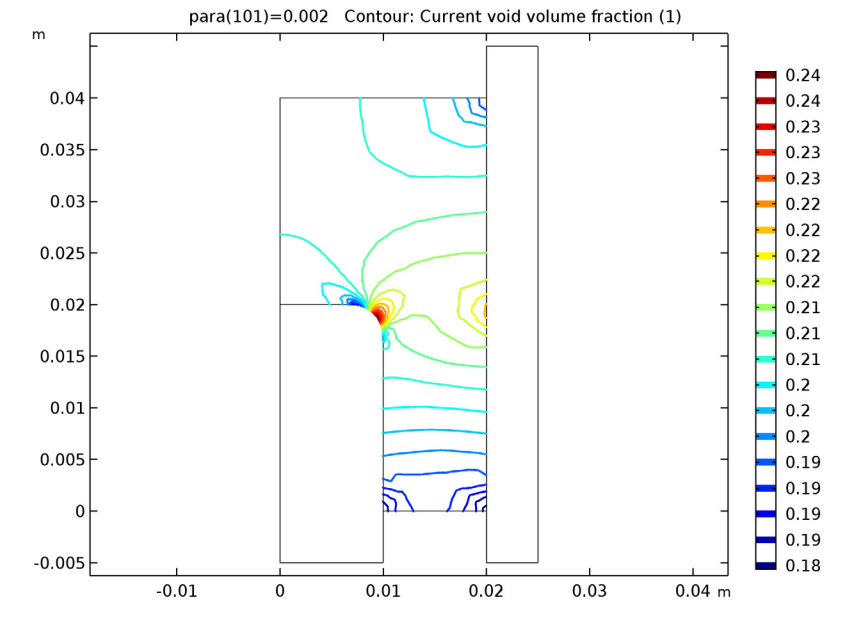
压实过程结束时的当前孔隙体积分数。
体积分数随着时间的变化。
最后,我们查看工件内的 von Mises 应力。结果表明,压制越紧实的地方应力越大。
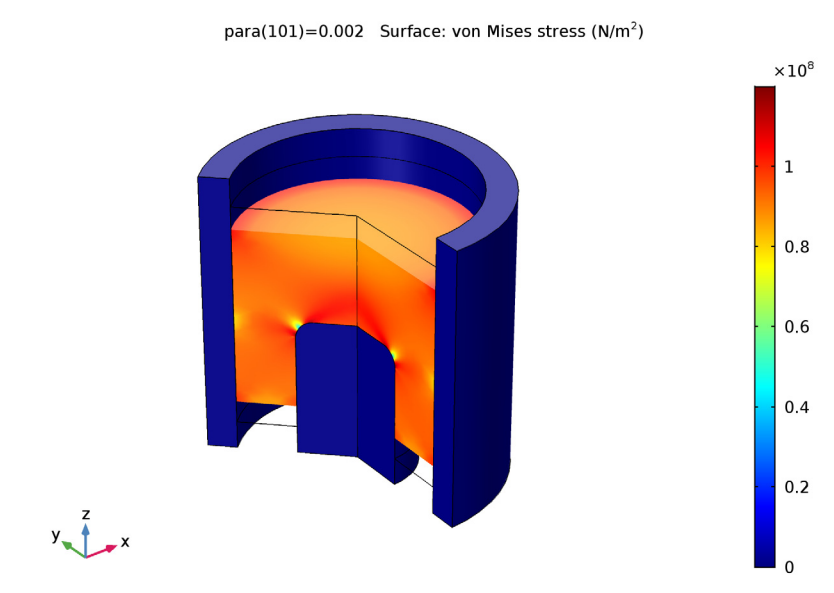
工件内的 von Mises 应力。
利用多孔塑性模型分析粉末压制
选择合适的塑性模型对于模拟粉末压制非常重要;模型最好在分析工具进行了预定义,并且可直接使用。为了满足用户的建模需求,COMSOL Multiphysics® 5.3版本提供了五个具有各种不同的孔隙率值的新模型。
如需了解如何使用多孔塑性模型,请尝试此博客文章介绍的案例。



评论 (2)
志坤 周
2024-06-11我应该在哪里看五种多孔介质模型的区别呢
Kaixi Tang
2024-06-14 COMSOL 员工您好,在添加多孔塑形后,您可以尝试点击软件界面右上角的“问号”打开帮助文档,文档中有关于多孔塑形本构的具体介绍和说明。