带标签的博客文章 CFD 模块
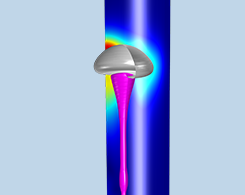
利用仿真技术阻止微流控装置中的气泡夹带现象
微流控设备会受到气泡的破坏。事实上,如果气泡夹带在微流控设备中,可能会导致设备发生故障。Veryst 工程公司创建了一个 CFD 模型来研究这个过程。
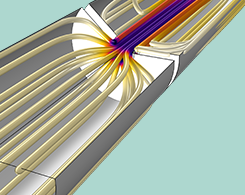
油脂浸洗鸡尾酒工艺在工业上的应用
近十年以来,油脂浸洗鸡尾酒逐渐成为一种流行风潮。调酒师使用这项技术可以制作各种各样的鸡尾酒饮料,例如 Benton 老式培根波旁威士忌(Benton’s Old-Fashioned, a bacon-infused bourbon cocktail)和温和山核桃黄油波旁威士忌
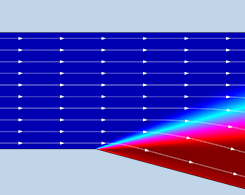
使用基准模型验证膨胀波结果的准确性
当超音速流围绕凸角转动时,会产生膨胀风扇。 您可以使用经过验证的基准在 COMSOL Multiphysics® 中分析这种现象。
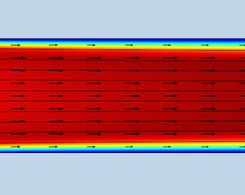
CFD 仿真中如何设定流体压力
众所周知,在 CFD 仿真中常涉及两种压力:绝对压力和相对压力。通过实验测量流体中压力的方法有许多种。在建立 CFD 模型时,正确地设定压力对定义边界条件和定义材料特性非常重要。 今天,我们将解释相对压力和绝对压力之间的区别,讨论 COMSOL Multiphysics® 软件为什么使用相对压力求解 CFD 问题,以及在模拟中什么时候使用不同定义的压力。 绝对压力和相对压力有什么区别? 在流体力学中,压力是指流体中单位面积表面上所承受的力。使用 COMSOL Multiphysics,我们可以通过求解流体流动的控制方程,纳维-斯托克斯方程,从而确定描述流动的速度和压力场。 CFD 问题中涉及的压力,通常主要有两种:绝对压力和相对压力。 绝对压力 绝对压力是指以绝对真空为基准直接测量的压力,即流体的真实压力。例如,如果我们使用气压计测量某一日的室外压力,会看到气压计的绝对读数大约为 1 个大气压或 101.325kPa,该值与海平面上的大气压相等。绝对压力为零代表真空。 使用气压计测量从 950mbar 到 1050mbar 的室外压力(1 mbar = 100 Pa)。图片来自 Langspeed,通过Wikimedia Commons在CC BY-SA 3.0下获得许可。 相对压力 相对压力是指相对于参考压力的流体压力。表压力是相对于环境压力测得的压力,即以环境压力为参考的相对压力。通常,相对压力用于表征封闭系统中的压力水平。我们可以使用压力表测量相对压力,以将内部压力与周围压力相关联。 压力表,在压力控制站测量相对压力。注意刻度盘如何从零开始,零刻度代表系统压力等于参考压力水平。图片由 Holmium 提供-自己的作品。通过Wikimedia Commons在CC BY-SA 3.0下获得许可。 绝对压力和相对压力的关系可表示如下: PA=p+pref 如果使用真空作为参考压力,则绝对压力和相对压力相等。大多数情况下,参考压力设置为大气压,通常是环境压力。 接下来,我们来看一下如何在 COMSOL Multiphysics 中描述这些压力定义。当我们计算一个流体流动问题的解时,COMSOL® 软件首先会求解速度分量(u,v,w)和相对压力(p)。在后文中,我们将解释,通过使用相对压力(而不是绝对压力)作为因变量,可以在建模中提高压力描述的准确性。然后,我们可以使用相对压力值作为模型的初始值和边界条件,下面,我们将举例说明。 在 COMSOL Multiphysics® 中表征流体压力 我们来看一个如何在 COMSOL Multiphysics 模型中恰当地将相对压力和绝对压力作为变量的示例。为了演示这些概念,我们使用一个简单的模型来说明。在模型中,空气以 1m/s 的入口速度流入通道并流出到绝对压力为 1 个大气压的环境中。除了我们假设两个对称的短入口段外,模型顶部和底部的边界均为无滑移通道壁。设置入口段是为了避免不一致的边界条件。(如果我们在防滑边界附近定义一个笔直的入口速度曲线,就会出现不一致的边界条件。) 有空气流通的通道示意图。 在此模型中,相对压力的变量名称为 p,绝对压力的变量名称为 spf.pA。在层流 接口的设置中,我们看到要求解的因变量是速度分量(u,v,w)和相对压力(p)。 因变量设置窗口。 在下图中,我们可以看到,参考压力水平默认设置为 1[atm]。该参考压力水平用于计算绝对压力:spf.pA = p + spf.pref。 我们还将可压缩性设置为弱可压缩流,这意味着空气的密度取决于温度和参考压力。要了解不同可压缩性设置的更多信息,请参阅上一篇博客文章。 可压缩性和参考压力设置。 现在,我们可以指定边界条件。在入口处,将法向速度设置为 1m/s。对于初始条件和出口边界条件,由于使用默认设置,因此需要输入相对压力。即,使用一个参考压力。当加上出口条件时,我们看到相对压力的默认值为 p=0,相当于绝对压力等于默认的参考压力为 […]
黑啤酒杯中的泡沫会上升,还是下降?
你有没有注意过某些烈性啤酒的气泡是如何沉到杯子的底部,而不是上升到顶部的?我们用流体流动仿真来解释这一现象。

计算质量和能量守恒的方法
拟有没有想过如何计算流体流动仿真的质量守恒,或共轭传热模拟的能量平衡?如果是,请继续阅读 >>

使用布辛涅斯克近似模拟自然对流
今天,我们将比较的 布辛涅斯克近似 与完整 纳维-斯托克斯方程 在自然对流问题中的应用。本文介绍了如何在 COMSOL Multiphysics 软件中实现布辛涅斯克近似,以及使用布辛涅斯克近似的潜在优势。 应用示例:方形空腔中的自然对流 在下面的示例中,我们将使用一个耦合了纳维-斯托克斯方程和传热方程的模型来模拟带有加热壁的方形空腔中的自然对流。空腔左壁和右壁的温度分别为 293K 和 294K;顶壁和底壁是隔热的;流体是空气,侧面的长度为 10cm。 我们将使用此模型比较三种不同建模方法的计算成本: 求解完整的纳维-斯托克斯方程(方法1) \rho \left( \frac{\partial \mathbf{u}} {\partial t} + \mathbf{u} \cdot \nabla \mathbf{u} \right) = -\nabla p + \nabla \cdot ( \mu (\nabla \mathbf{u} + (\nabla \mathbf{u})^{T}) -\frac{2}{3} \mu (\nabla \cdot \mathbf{u})\mathbf{I}) + \rho \mathbf{g} 用压力变换求解完整的纳维-斯托克斯方程(方法2) \rho \left( \frac{\partial \mathbf{u}}{\partial t} + \mathbf{u} \cdot \nabla \mathbf{u}\right) = -\nabla P + \nabla \cdot ( \mu (\nabla \mathbf{u} + (\nabla \mathbf{u})^{T})- \frac{2} {3}\mu (\nabla \cdot […]

介电泳分离
电泳是一种通过电场来控制电中性粒子的运动的现象。了解如何在直流和交流电场中模拟这种效应。
