带标签的博客文章 优化模块

如何使用参数估计研究步骤进行逆向建模
创建仿真时,通常首先从构建正向模型开始,设定各种输入值,然后查看结果。但是,如果我们已经通过实验或调查得到一组结果(如材料属性),然后想通过仿真找到能得出相同结果的输入数据,该怎么办?本篇博文,我们将通过一个视频教程向您演示如何在 COMSOL Multiphysics® 中使用 参数估计 研究步骤帮助我们建立逆向模型,并求解模型的最佳输入值。 视频教程:在 COMSOL Multiphysics® 中执行参数估计研究 使用参数估计研究步骤进行逆建模 假设我们需要通过仿真得到有一组外部数据(来自实验测量值或参考数据集),我们该怎么做?这时,我们可以使用逆向建模 。顾名思义,逆向建模就是对问题采取逆向建模的方法,即求解的不是输出值,而是输入参数。 为了获得所需的仿真结果,我们可能需要调查或通过实验得到几种模型输入值,例如材料属性。在求解这些输入值时,为了使外部数据和仿真结果非常接近,我们会寻找最优值。很自然,我们想到了使数据之间差值的平方和最小的方法来求解。因此,将问题构建为最小二乘优化问题是一个有效的建模策略。为了简化设置和求解问题的过程,我们可以使用 COMSOL Multiphysics® 软件中的参数估计 研究步骤。 注意:要使用 参数估计 研究步骤,研究的问题必须与时间有关,并且需要具有COMSOL 软件优化模块的许可证。另外,还需要通过一个插值函数或用户定义的参考表达式来引入一组参考数据。请注意,参考数据必须是与时间相关或者是一个单变量函数。 参数估计研究步骤的 “设置”窗口。 参数估计 研究步骤对于各种逆向建模问题(主要是参数估计)非常有用,其目的是估计模型所需输入(即参数)的值,这可以帮助我们深入了解参数的数值大小(以及属性)影响目标函数的方式。 参数估计 功能最典型的用途之一可能是曲线拟合或类似的数据拟合应用。此过程涉及将函数拟合到一系列数据点。函数的拟合是通过估算函数中的系数值来完成的,本质上是将参数化的解析函数拟合到一个数据集合。通过将曲线拟合到一组数据点,我们可以对函数以及无法得到确切数据的区域进行插值。 在本文开头的教程视频中,我们通过一个优化后的 弯头支架教程模型 演示了参数估计的使用。在进行这项研究之前,我们需要正确定义问题…… 在 COMSOL Multiphysics® 中执行参数估计研究 在 COMSOL 中执行参数估计研究通常包括三个主要步骤: 预研究:准备定义,例如参数、变量和函数 研究设置:自定义研究的各项内容并进行计算 后期研究:进行后期处理使结果可视化,比较模拟值和实验结果,并提取最佳的参数估计值 下面,让我们看一下如何完成这些步骤,以及在模型中设置 参数估计 研究步骤时需要考虑的重要因素。 步骤 1:参数估计预定义 在进行参数估计研究之前,我们必须先定义问题。这通常涉及创建参数、函数和变量的组合。首先,我们定义模型的输入参数,它们是需要被估算的值;接下来,通过定义一个参考函数或表达式来引入外部数据;最后,定义一个从仿真结果中提取并评估的输出变量,并将其与测量得到的输出数据进行比较。 在文中开头的视频中,我们对弯头支架进行了瞬态传热分析。然后将传热仿真得到的模拟数据与实验数据进行了比较,该实验数据用于评估材料的热导率值。 在固体传热 节点中,导热系数用 k 表示。因此,我们定义一个名为 k 的参数,输入一个 k 的粗略估计值,并在适当的节点中用它来定义导热系数。 左:用于参数估计研究的参数,包括用于估计导热系数的参数 k。右:在节点(名为实体 1)使用参数 k 定义需要估计的材料属性。 接下来,为了将外部文件中的数据引入到 COMSOL® 软件中,我们创建了一个定义。在本例中,参考数据是一个与时间相关的温度测量值的集合,这些值包含在一个用逗号分隔(CSV)的文件中。通过将 插值 函数添加到模型组件中,然后使用从文件加载 按钮,可以快速轻松地将这些数据输入 COMSOL Multiphysics。数据以表格格式自动导入,第一列为时间,第二列为温度测量值。 通过“插值“ 函数将参考数据引入仿真中”从文件加载”按钮用于将外部文件导入函数。 在单位 部分,我们只需要简单的输入参数(时间)和函数(温度)的相应单位,无需设置函数的 插值和外推 选项,因为研究仅计算函数的自变量或 t 列中明确指定时间点的差值。因此,数据点之间的平滑度和超出数据范围的函数行为设置并不重要。 现在,我们需要定义一个表达式,以从仿真结果中提取温度量(此量随后将与内插函数中的温度测量值进行比较)。我们要提取并用于比较的量是支架右上端表面的平均温度。 由于要获取量(温度)的平均值,因此我们首先在 […]
扬声器中磁路的拓扑优化
今天的消费者需要既精致又轻便的扬声器。 拓扑优化可帮助工程师设计实现此目标的组件。

使用最小二乘目标进行多参数优化
了解如何使用多参数优化来估计参数,这将根据实验参数的基础数据文件自动调整您的模型。

寻找最佳的管道保温层厚度
为了长距离运输石油和天然气等产品,需要对管道进行适当的保温处理。使用COMSOL®来寻找管道保温的理想厚度。
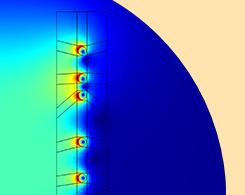
如何优化电磁线圈的间距
在设计电磁线圈时,我们可能想要调整线圈的位置,以便在特定的空间区域内获得所需的磁场强度。这可以使用 COMSOL Multiphysics® 软件附加的“AC/DC 模块”和“优化模块”产品,结合参数和形状优化来实现。接下来,让我们看看如何操作。 初始线圈设计和优化问题 假设我们的任务是设计一个线圈,使沿着部分中心线的磁场尽可能接近目标值。我们在之前的博客文章中介绍过,可以通过调整每匝线圈的电流来实现,但是,文中讨论的方法要在设计方案中为每匝线圈设计单独的电流控制。其实,我们可以对整个线圈使用单一的电流控制,并沿轴向调整线圈的间距来实现。 10 匝轴对称线圈。目标是改变中心线(绿色)处的磁场。 上图所示的线圈就是我们将要分析的案例。10 匝轴对称线圈由单个电流源驱动; 也就是说,流经每匝线圈的电流相同。最初的线圈设计将直径为 1cm 的线圈间隔为 S0 = 4cm 的距离。由于线圈是轴对称结构(我们仅对关于 z = 0 平面对称的解感兴趣),我们可以使用下图所示的简化计算域。 计算模型。我们想要改变五个线圈的位置和线圈电流。 我们的优化目标是通过改变五个线圈的线圈电流和 z 位置,使沿着一部分中心线的 Bz 场尽可能接近期望值 B0。每个线圈可以移动的距离为 ,相邻线圈之间必须存在 G0 的间隙,因此第一个线圈的偏移量具有不同的下限。我们还需要对峰值电流进行约束,将电流限制在大于零的范围内。虽然从物理上讲,没有必要将电流限制在大于零的范围内,但这样做是一个很好的优化建模的技巧,因为这样可以保持受限的设计空间更小。 更正式地讲,这些陈述可以写成: \begin{aligned}& \underset{I, \Delta Z1, \ldots ,\Delta Z5}{\text{minimize:}}& & \frac{1}{L0} \int0^{L0} \left( \frac{Bz}{B0} -1 \right) ^2 d l \\end{aligned} \begin{aligned} & \text{subject to:}& & -(S0-G0)/2 \le \Delta Z1 \leq \Delta Z{max} \\end{aligned} \begin{aligned} & & & -\Delta Z{max} \leq \Delta Z2, \ldots ,\Delta Z5 \leq \Delta Z{max} \\end{aligned} \begin{aligned} & & & G0 \le (Z5-Z4) \\end{aligned} \begin{aligned} & & & […]
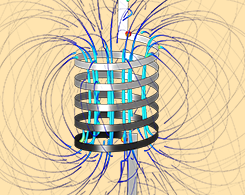
优化电磁线圈电流的 3 种方法
如果使用 COMSOL Multiphysics® 软件及其附加的 AC/DC 模块与优化模块进行电磁线圈设计,您将能够快速地提出优化的迭代设计。今天,我们将研究如何通过改变线圈的驱动电流来设计线圈系统,以实现所需的磁场分布,并介绍三种不同的优化目标和约束条件。如果您对线圈模拟或优化感兴趣,这篇博客将满足您的好奇心!

如何用 COMSOL 仿真 App 分析热电冷却器设计
仿真 App,如用于热电冷却器设计的仿真 App,可用于测试各种参数,以便优化用于特定用途的设备。
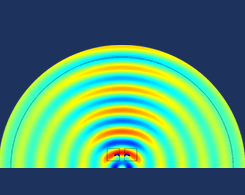
如何在仿真研究中使用声学拓扑优化
今天,瑞声达听力集团的客座博主 René Christensen 跟我们一起讨论声学拓扑优化的重要性,以及如何在 COMSOL Multipysics 中应用声学拓扑优化。 拓扑优化是一种强大的工具,通过使用这种工具,工程技术人员能够找到与其应用相关的问题的最佳解决方案。本文中,我们将深入研究声学方面的拓扑优化,以及如何最优分配声介质来获得所需的响应。下面几个例子将进一步说明这种优化技术的潜力。
