
每年,来自全球各地的网球运动员都会齐聚美国网球公开赛,这也是网球界历史最悠久、规模最大的网球锦标赛之一。随着 2015 网球锦标赛的临近,我又想起了自己打网球的一些经历,每次击球的体验都不太一样。这只是我自己的主观感觉?还是这背后也存在相应的物理解释?在本篇博客中,我将通过建模与仿真来说明如何用所谓的“甜区”来解释这种感觉。
网球拍的振动节点
根据机械振动理论,振动节点是指当有波传过时不会发生位移的点。由于球撞击球拍产生波,使球拍开始振动并摇摆。当球拍的一端被运动员握在手中时,查看球拍的振型,此时可以找出振动位移为零的点,即在振动期间内任意时刻的振幅为零。下面是使用 COMSOL Multiphysics 模拟计算得到的三种不同振型:
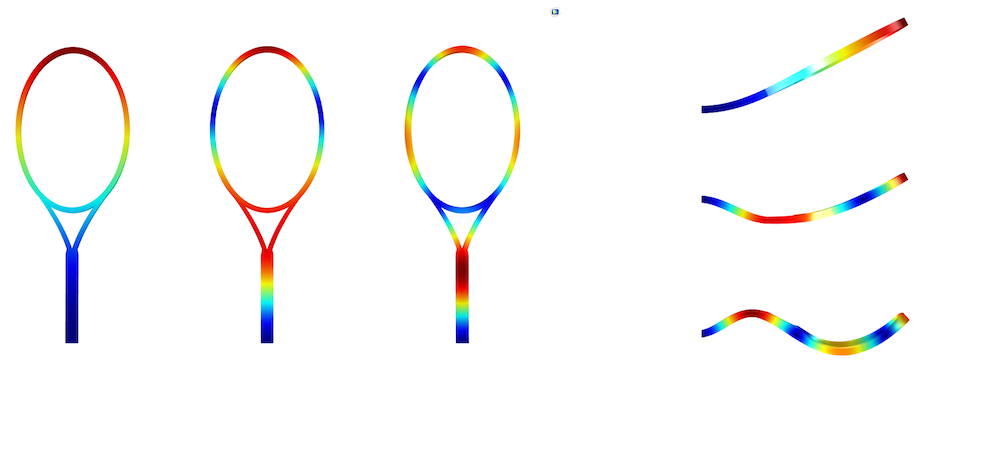
从左到右、从上到下的顺序分别表示网球拍的前三种振型。基础振型的频率为 15 Hz;第二种振型的频率为 140 Hz;第三种振型的频率为 405 Hz。
如上图所示,许多点都表现出了这一行为。那为什么我说的好像只存在一个振动节点呢?现实中其实存在无穷多的振动节点。当受到撞击后,球会产生无数个不同频率的谐波。一次会激活无限数量的频率,但哪个振动节点才是“甜区”呢?是基础振型节点还是不同谐波交叉后产生的节点?
很显然,基础振型节点不会是甜区:它位于手柄处。您可以尝试用手柄击球过网。运气非常好的话可能会成功,但这个概率非常低。同时,第二个振型还包含两个节点:一个位于手柄处,另一个位于靠近拍头处的网线处,后者被认为是甜区。用这一点击球时,所有球员基本上都不会感觉到振动。
当然,更高频率振型下也存在振动节点,如上方得到的第三种模式所示。但随着振型固有频率的增加,振幅将显著下降。下图显示了一个梁结构对持续 5 ms 的正弦式载荷的频率响应,这相当于球撞击球拍的时长。对于高于 300 Hz 的频率,振幅几乎为零。也就是说,第三种振型或更高频率振型的影响可以忽略。不论球撞到哪个位置,即使是在振型达到最大振幅的点,更高的振型由于没有任何激发,所以不会带来任何影响。
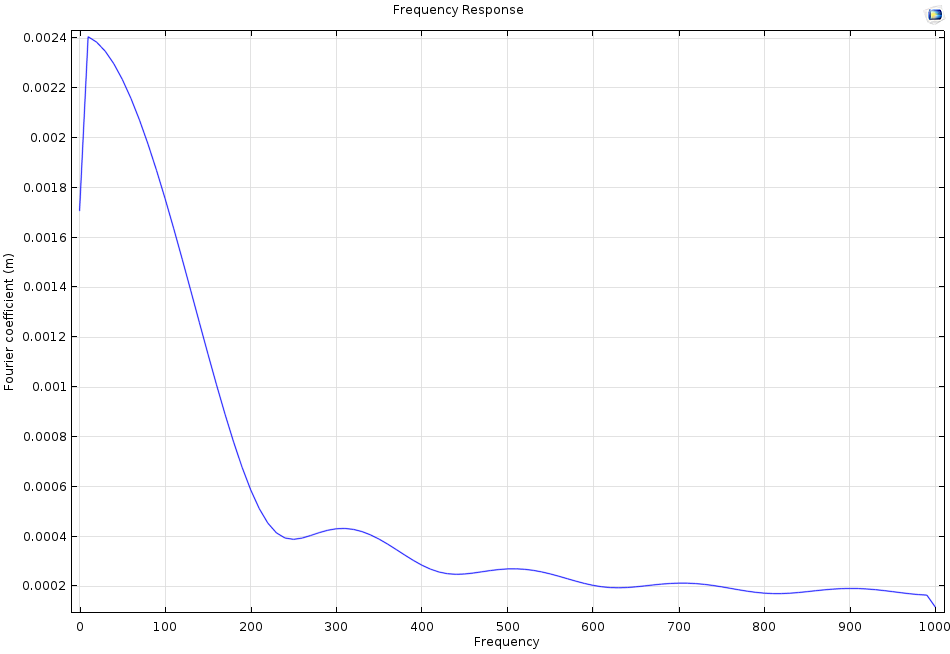
绘图显示了对持续 5 ms 的正弦式载荷的频率响应。
网球拍的撞击中心
当网球击中球拍某点时,如果没有其他作用力,球拍将沿指向另一端的轴线旋转。随着在击点处球与球拍的质心距离逐渐接近,击点与旋转轴的距离将会缩短。当球正好撞到质心时,球拍将发生平移而非旋转。从数学角度来看,旋转的中点位于球拍的无穷远处。
即便如此,我们还是能找出一个撞击位置,它将在靠近手柄的端点处产生一个旋转中心,也就是选手的握拍位置。我们可以在质心的特定距离处找到一个位置,当球撞击球拍上的这个点时,会得到一个靠近手柄端点的旋转中心。这一点被称作 撞击中心 (COP),有时也会被看作一个甜区。当球拍沿靠近球柄端点的旋转中心旋转时,会绕开选手的手,因此手不会受力。

对比 20 世纪 70 年代流行的老式木质网球拍与拍头更大的现代球拍。新的设计用于将撞击中心从球拍的外框移到靠近网球线的中心。图片由 CORE-Materials 提供,通过 Wikimedia Commons 分享。
现在,让我们从力学角度分析到底发生了什么。我们假定球拍可以作为一个刚性梁结构模拟。
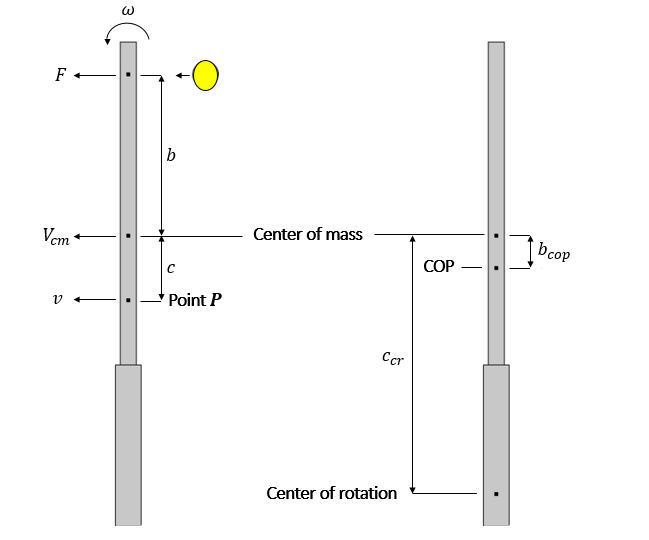
梁结构示意图。图中定义了将用于以下方程的参数。
当与质量为 M 的质心距离 b 处施加力 F 时,此时质心会按 V_{cm} 速度发生水平移动。根据牛顿第二定律,
此外,力 F 会绕质心产生一个扭矩:
其中,I 是梁沿旋转轴的转动惯量,\omega是角速度。考虑点 P,它与质心的距离为 c。点的速度 v 为 v=V_{cm}-c\omega,得到:
由于旋转中心对应于不存在平移加速度的点,COP 与质心之间的距离为 b_{cop},可通过以下公式计算
其中,c_{cr} 是旋转中心与质心之间的距离。根据质心与理想旋转中心(抓柄端点处)的距离,我们可以直接判断出特定球拍形状中 COP 的位置。
功率点
我们有时也将功率点称作第三个甜区,它是最佳的弹跃点。换言之,球接触到这个点后会产生最好的弹性。从数学的角度来看,功率点定义为拥有最高回弹系数 (COR)的点,COR 就是回弹高度与球的入射高度之比。回弹系数是所有会影响球速的设计元素综合作用的结果,所以非常重要;它还为我们提供了一个综合视角来考察所有因素,设计工程师将无需单独了解每个参数的影响。
功率点位于球拍的拍喉处,靠近质心。该点与拍喉的距离越近,刚度越高,由于球拍变形造成的能量损耗越低。当球击中球拍时,冲击能会分为球、球拍及网球线上的动能和弹性能(变形能)。功率点处的变形很小,因此球拍能将几乎所有的动能传回球。
回快球时,功率点的作用很大。实际中,如果必须回一个快球,您将不会有太多时间来调整球拍位置以及准备回球,所以只能选择在球打来时把它打回去。需要注意有一点很重要:球越靠近功率点,回球质量越高。
哑点
本文所介绍的球拍中最后一个很有意思的点是哑点。球击中哑点时,完全不会发生回弹。球传递的所有能量会传到球拍,不会有能量返回到球上。这是由于球拍在哑点处(通常较靠近端点)的等效质量等于球的质量。从力学的角度来看,哑点处产生的力与加速度之比等于球的质量。
为了更好地理解这一物理现象,我们将假定一个理想碰撞:初始速度为 V_0、质量为 m 的刚性球与另一个质量相同但处于静止态的刚性球发生碰撞。根据能量守恒和动量守恒得到:
因此,它变为
如果球与另一个质量相同但处于静止态的球发生碰撞,球会突然停止,并将能量全部传递给另一个球。因此,当球碰到静止球拍上的哑点时,完全不会发生回弹。因此用这个点来回球是非常遭的选择。但另一方面,当您希望击打静态球时,比如在您的发球局中,哑点能非常高效地将动量能从球拍传递至球中。
在您的接球局,哪个才是最佳击球点呢?这并非只有由甜区的数学所确定。大多数情况下,答案将相当靠近端点处。因为您挥臂的方式,球拍端点处的速度会远高于拍喉处的速度。因此,较高的撞击速度和良好的动量传递属性共同确定了这个最优点。
盘点-局点-破发点
现在,我们已经深入了解了这三个非常出名的球拍甜区背后的物理含义。在振动节点,传递至网球选手及手臂处的不适振动最少。在撞击中心点,对运动员手臂的初始冲击也是最小。最后,在功率点,球会以最快的速度发生回弹。
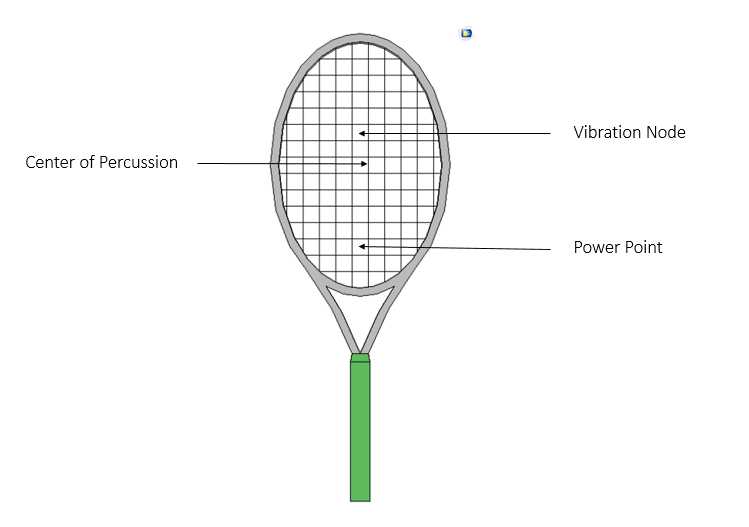
网球球拍中甜区的位置。
正式比赛前…
如果您希望打一场精彩的比赛,您可以继续阅读以下内容来提升您的网球技能:
- 网球选手的网球科学,H. Brody.
- “网球拍的物理学“,H. Brody.
- “网球拍的物理学 II:”甜区“,H. Brody.
- “网球拍的物理学III:球与拍的互动“,H. Brody.



评论 (0)