多孔介质中的热平衡与热非平衡传热

多孔材料的应用越来越广泛，因为它适用性强、成本低，具有特殊的热特性。例如，由于具有优异的力学和热性能，泡沫材料在不同航空应用中的使用日益增加。电动汽车的电池中也包含多孔结构。 在自然界中，我们也发现了例如土壤，岩石和木材等各种各样的多孔材料。使用多孔材料的应用通常是利用其热性能。许多工业应用都要求多孔材料具有优异的热性能。

微观尺度上的热量传递

让我们从微观层面来研究多孔结构中的热量传递。在上一篇博客中，我们从宏观尺度上验证和探究了多孔介质的流动方程。在该示例中，由于流动是等温的，因此我们不考虑孔隙几何结构对热量传递的影响。流体与固体的的热性能存在明显差异，因此，研究流体与固体之间的相互作用对于理解热量如何在多孔介质中传递至关重要。

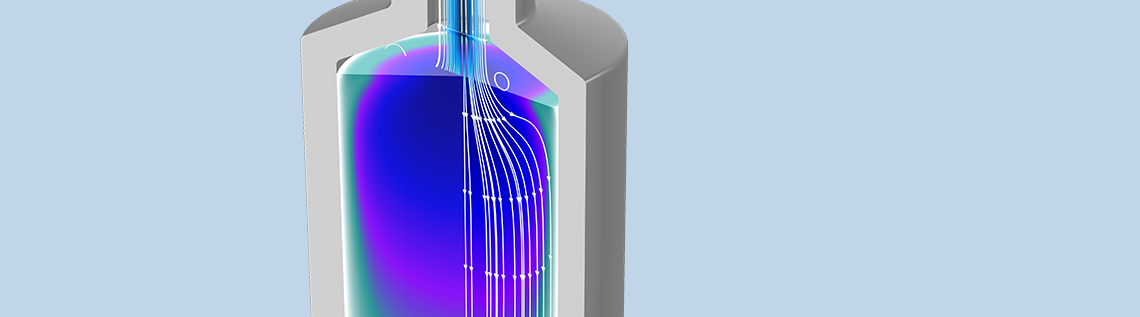
一个冷却的多孔结构的温度演变过程。初始局部热非平衡随着时间的变化达到热平衡。

本文我们的研究示例与上一篇博客中的相同，但本示例中注入的流体比多孔基质热得多。可以观察到，刚开始多孔基质 T_\textrm{s} 的温度和流体的温度 T_\textrm{f} 不同，但随着时间变化二者逐渐达到平衡。当然，这取决于边界条件以及流体和固体的热性质。在许多应用中，该假设 T_\textrm{s}=T_\textrm{f} 是有效的，我们称其为（局部）热平衡；而在另一些应用中，T_\textrm{s}\neq T_\textrm{f}，我们称其为（局部）热非平衡，其中“局部”是指温度 T_\textrm{f} 和 T_\textrm{s} 的逐点比较。

热平衡条件下的热量传递

在假设局部热平衡条件下，我们只需要一个方程来描述整个（固体和流体）多孔结构的平均温度。基于能量守恒以及混合原理，传热方程可以使用下式描述

(1)

显然，这与我们所熟知的传热方程非常相似。流体和多孔介质的热特性共同被视为有效的特性，即有效体积热容和有效热导率。

式中，指数 \textrm{f} 和 \textrm{s} 分别代表流体和固体，\rho 是密度 ，C_p 为恒压下的热容，\theta_\textrm{s} 为固体体积分数。假设多孔介质完全饱和，孔隙率对应于流体体积分数 \theta_\textrm{f} =1-\theta_\textrm{s}。

对于热量传递来说，有效热导率 k_\textrm{eff} 取决于多孔介质的结构以及固体和流体的热导率。COMSOL 软件内置了三种选项，可用于计算有效导热率k_\textrm{eff}:

1. 代表与热通量平行的固体和流体类型的体积平均值， k_\textrm{eff}=\theta_\textrm{s} k_\textrm{s} + \theta_\textrm{f} k_\textrm{f}
2. 垂直于热通量的固体和流体类型的倒数平均值， \frac{1}{k_\textrm{eff}}=\frac{\theta_\textrm{s}}{k_\textrm{s}} + \frac{ \theta_\textrm{f}}{k_\textrm{f}}
3. 任意几何结构具有相似热导率的固体和流体类型的幂定律，k_\textrm{eff}=k_\textrm{s}^{\theta_\textrm{p} }\cdot k_\textrm{f}^{\theta_\textrm{f}}

接下来，我们将通过使用一个假设的多孔材料示例来说明这三种平均方法，并将对不同选项的结果与计算值进行比较。

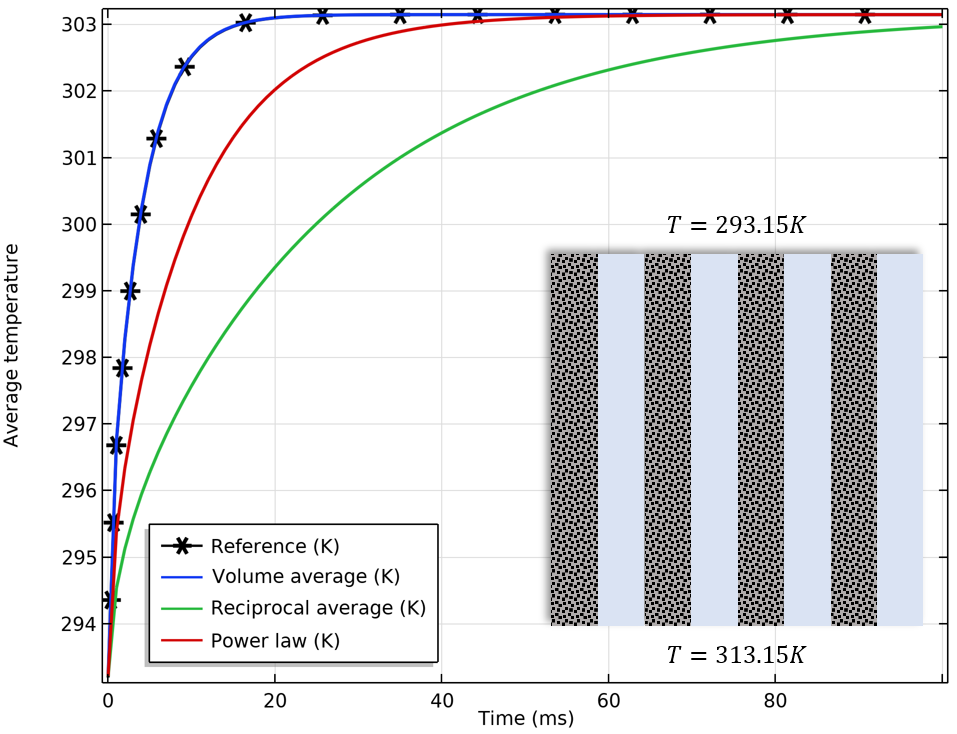
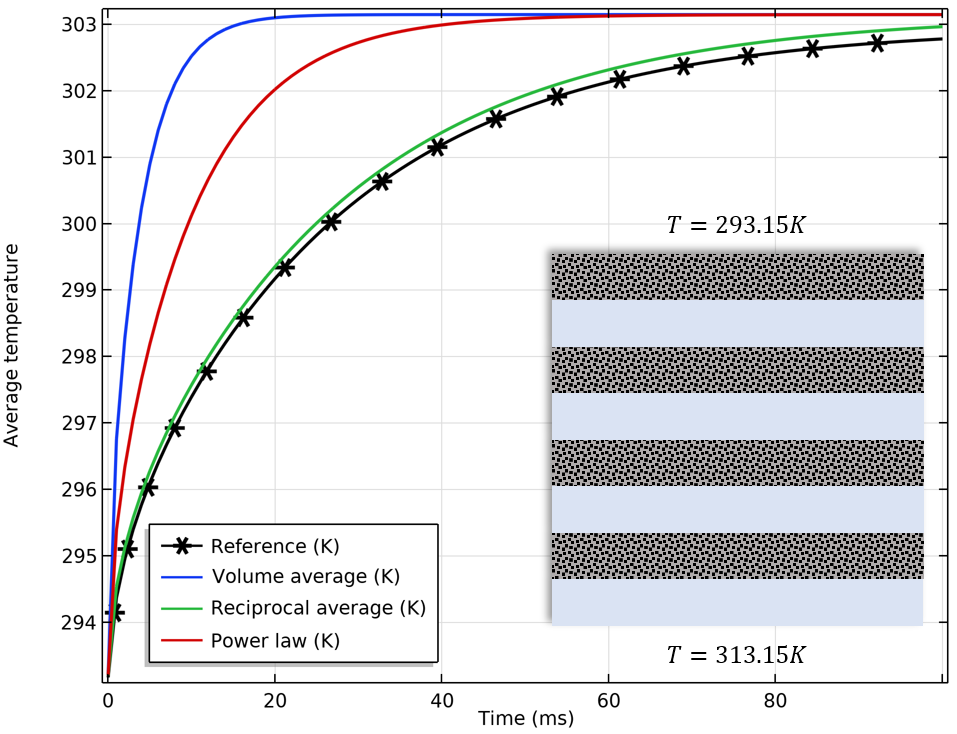
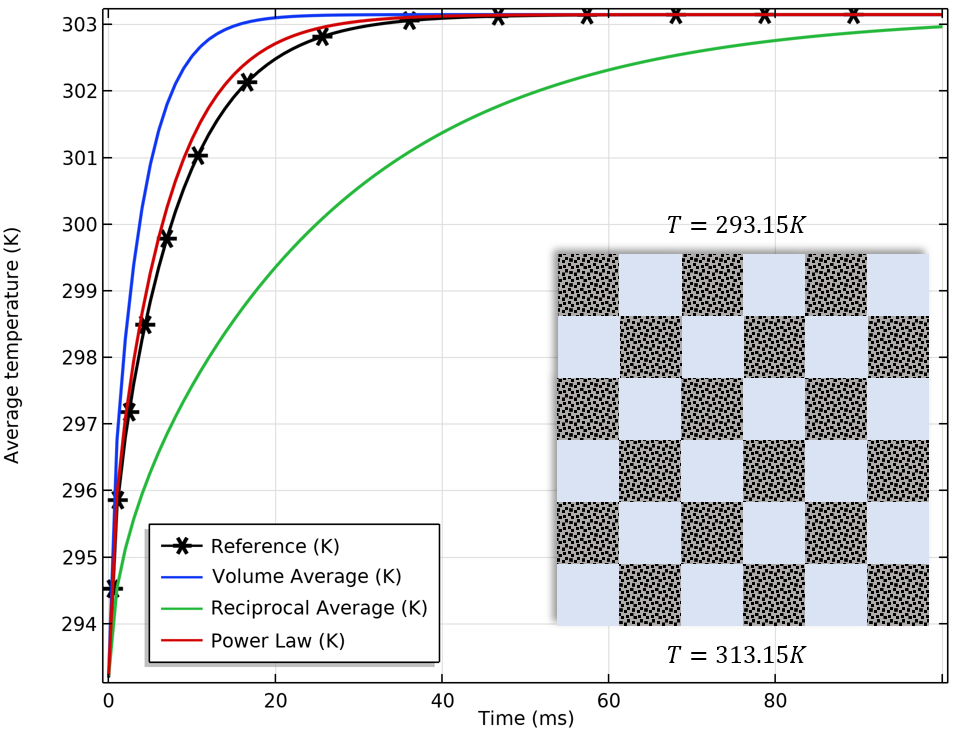
使用不同有效导热系数选项计算的平均温度的比较。从左至右：分别用并行、平行和格子的方式排列固体（灰色）和液体（蓝色）材料。热通量是由上下边界之间的指定温差产生的。

上述图示表明，结构越精细，由倒数平均值和幂定律计算的近似值越好。真正的有效导热系数介于体积平均值和倒数平均值之间，根据混合原理，分别对应上限和下限。如果对流是主要作用，那么混合原理对热导率的作用就不那么重要了。

多孔材料也可以由多种固体和不流动的流体组成，例如由不同矿物质和截留的液体组成的岩石。也可以在模型中考虑这一点，相应地也会计算有效材料属性。例如，可根据 k_\textrm{s}=\displaystyle\sum_{i=1}\theta_{\textrm{p}i}k_{\textrm{s}i} 计算由 i 种不同材料组成的多孔基质的体积平均导热率。

热分散

热分散是与多孔微结构有关的另一个重要作用。通常，对于以对流为主的状态，流体在孔隙尺度上遵循旋涡状路径，从而增强了固相和液相之间的热交换。宏观上，这是使用对传热方程 (等式1)，k_\textrm{disp}=\rho_\textrm{f} C_{p,\textrm{f}} D_{ij} 有贡献的额外的热导率来描述的, 其中 D_{ij} 是由于快速度场导致的分散张量。

将计算结果与之前博客示例中的平均温度结果进行比较。下图显示了通过微尺度方法计算出的平均温度，以及从包含和不包含热分散的平均宏观方程中获得的值。

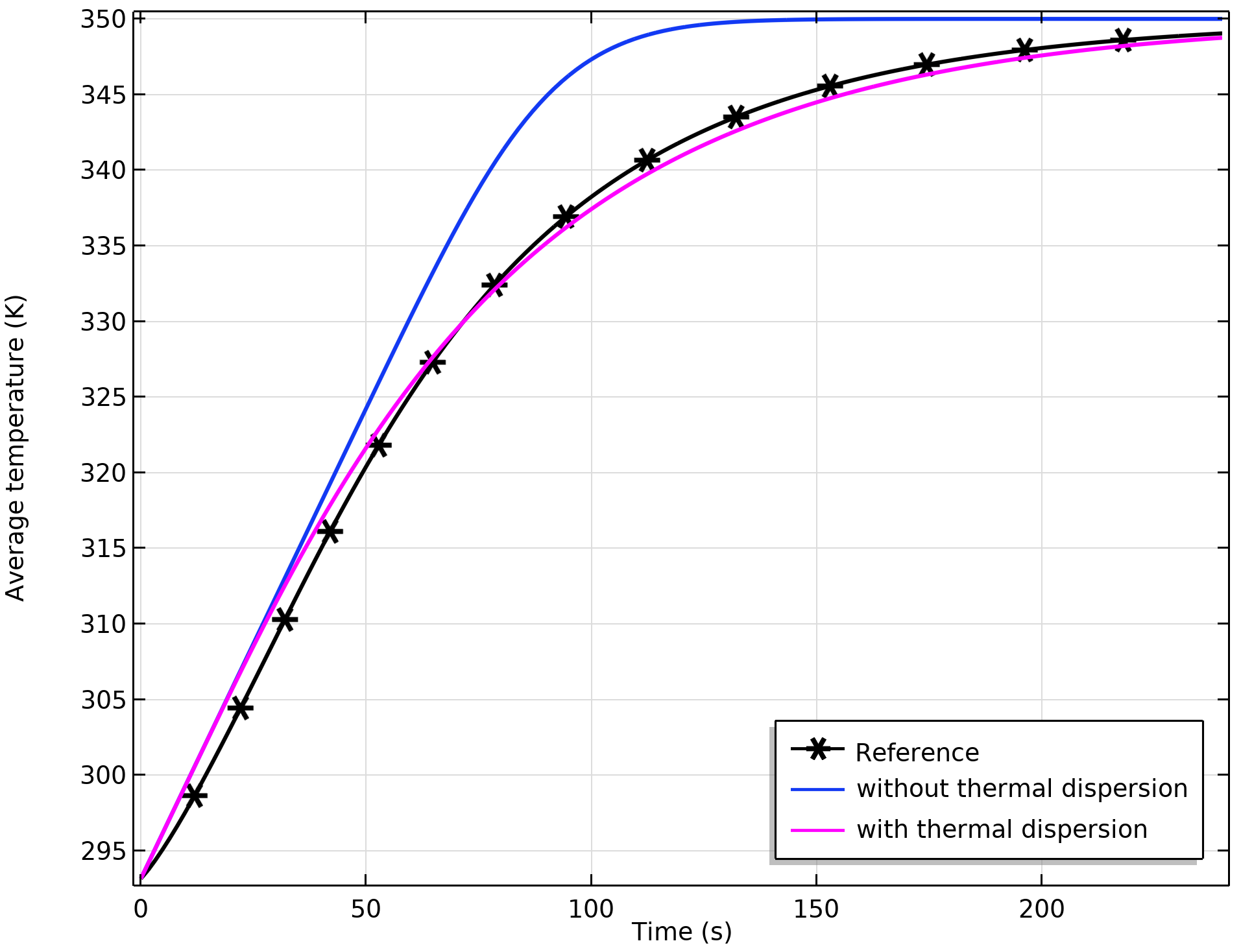
使用微观和宏观方法计算获得的平均温度比较。当包括热分散时，二者的一致性会更高。

热非平衡条件下的热量传递

如本文开头所述，局部热平衡并不总是能够达到。尤其是对于快速的非等温流动，在较短的时间尺度内，或在强烈依赖其他影响（例如相变）的情况下，固体和流体之间的温度差异可能很大。此时等式1并不完全有效，必须分别考虑各相的能量平衡，并且必须以显式方式考虑两相之间的热量交换。这是通过两个温度模型完成的。局部热非平衡 方法 (参考文献1)求解了两个温度场，并通过一个热源或热沉将其耦合起来：

固体和流体之间的热交换是通过等式右边的项考虑的，其中 q_\textrm{sf} (W/(m³ K)) 是间隙热传递系数，取决于相的热性质以及多孔介质的结构；更确切地说，是接触的比表面积。

非平衡传热的热能存储装置是这方面的一个很好的示例。该装置的工作原理如下：水在太阳能集热器中被加热，然后通过装有石蜡填充的胶囊，在水箱中循环。在装料期间，将胶囊内的石蜡加热到其熔化温度以上，太阳能就会以显热和潜热的形式被存储，从而可以在更长的时间内存储更多的能量。

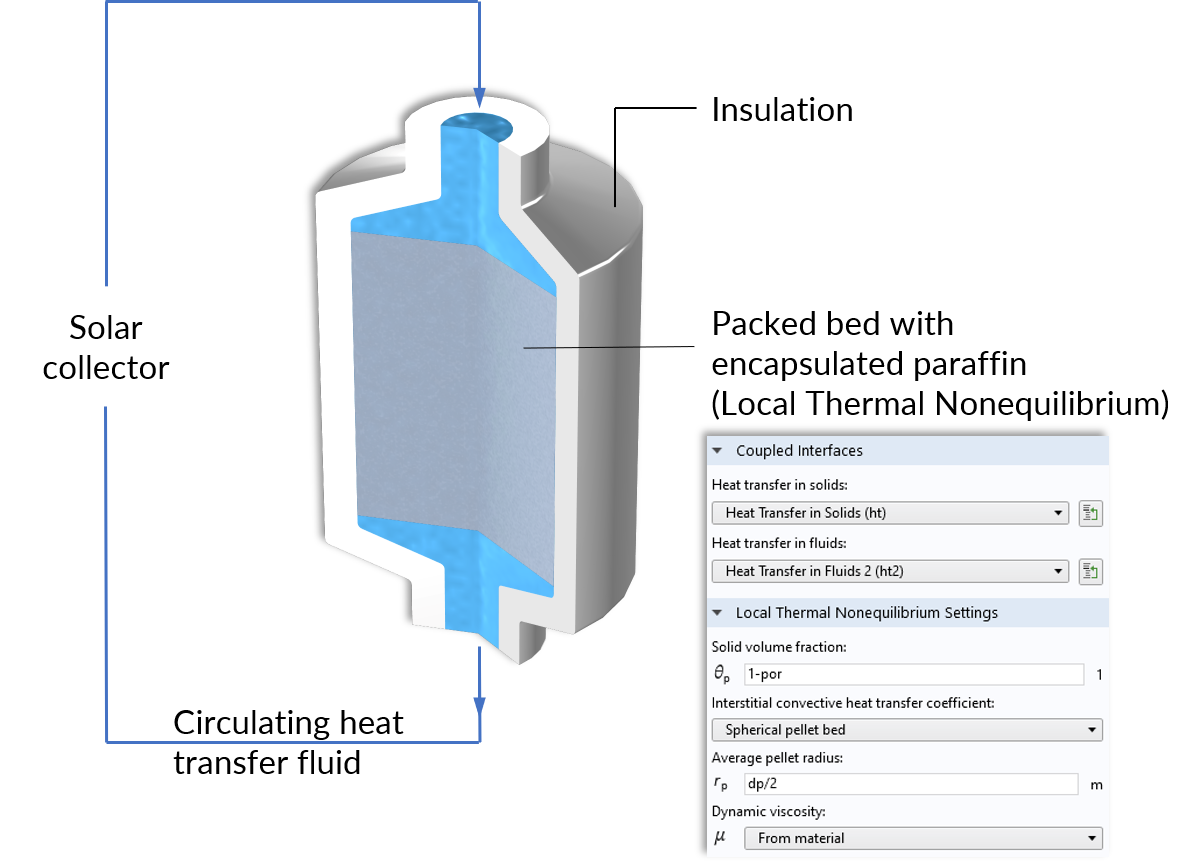
储热装置的运行原理和填充床的局部热非平衡多物理场耦合节点。

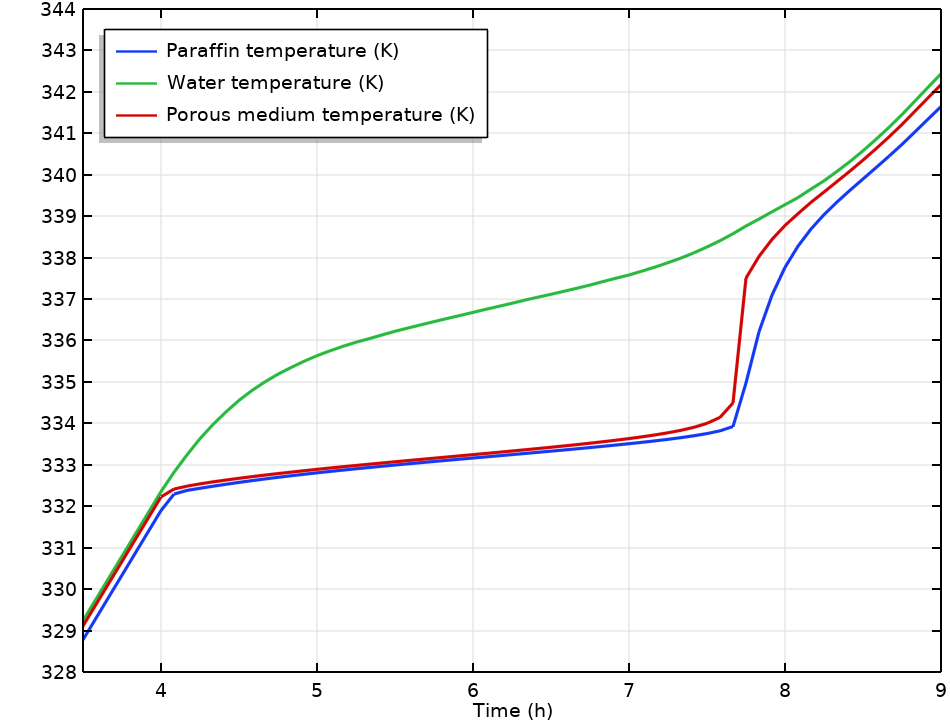
在储热期间，油箱中的石蜡、水和平均温度。

与水相比，包封的石蜡加热时间更长，因此仅靠水温无法估算出水箱充满之前的时间。水和石蜡中的热量传递可以通过局部非热平衡多物理接口耦合。

多孔介质传热建模

我们从微观和宏观两个层面进一步研究了多孔介质中的传热机理。具有有效热特性的宏观方程能够近似模拟多孔介质中的均匀传热。COMSOL Multiphysics®软件中还包含孔尺度流量的复杂计算。例如，可以通过计算传热方程来模拟表征体元 (REV) ，以获得大型、实际应用中的平均值。

参考文献

1. D. A. Nield and A. Bejan, Convection in Porous Media, 4^th ed. Springer, 2013.

动手尝试

单击下面的按钮，尝试模拟本文中介绍的填充床潜热存储模型。您可以在COMSOL 案例库中 下载 MPH 文件。