理解瞬态电磁激励选项

如果要模拟随时间任意变化的电信号，通常可以使用 COMSOL Multiphysics^® 软件中计算效率极高的电流 接口，通过一个瞬态研究来计算系统的响应。虽然软件中有多种不同的激励选项，但我们通常会考虑外加电流信号或沿传输线传播的电压信号。让我们来深入了解一下其中的原因。

目录

1. 前言
2. 电流激励
3. 电流中的电压激励
4. 传输线、集总端口和终端条件
5. 电路连接
6. 结束语

前言

本文，我们将探讨上一篇博客模拟射频加热的 5 种方法中使用的示例：对插入充满有损电介质材料样品的金属空腔中的同轴电缆进行频域激励。我们将使用相同的系统，在同轴电缆上施加各种类型的瞬态信号，并对使用电流 物理场接口和电磁波，瞬态 物理场接口计算的结果进行比较，主要是比较在计算材料内部的总损耗。比较这两个接口的原因是，电磁波，瞬态 接口求解的是麦克斯韦方程组的完整矢量形式，而电流 接口求解的是麦克斯韦方程组的简化近似值，即忽略磁场，仅求解标量电势。为降低这些示例的计算成本，该模型将被简化为二维轴对称模拟平面，如下图所示。

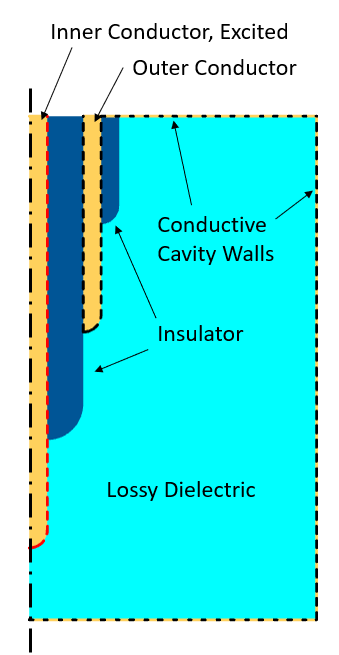
二维轴对称模拟平面示意图。

电流激励

如下图所示，我们首先通过指定一个随时间变化的电流来激励系统。信号最初为零，然后阶跃上升到最大值并保持不变。我们可以对该阶跃函数进行平滑处理，这将在后文中讨论。系统开始时处于未激励状态，即最初各处的场均为零。鉴于这种初始条件和输入信号，瞬态系统响应应该在足够长的时间后接近非零稳态解，相当于系统的直流激励。

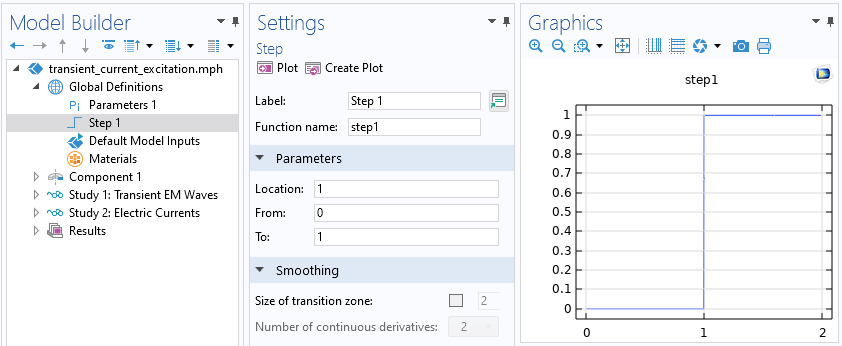
施加信号通过一个阶跃函数进行调制，该函数与模型维度不相关，函数值在 1 的时候从 0 跃升至 1。注意包括平滑选项，目前处于禁用状态。

我们首先使用电磁波，瞬态 接口建立模型，因为该接口可以表征到所有的电阻、电容和电感现象。该接口与之前使用的电磁波，频域 接口不同，它不包含阻抗边界条件，因为该边界条件只对频域有意义。虽然可以对金属导线进行显式建模，但我们将通过理想电导体 边界条件，将所有金属零件模拟为无损耗的理想导体。这样做是合理的，因为之前我们已经证明，在这种情况下，金属中的损耗相对来说可以忽略不计。

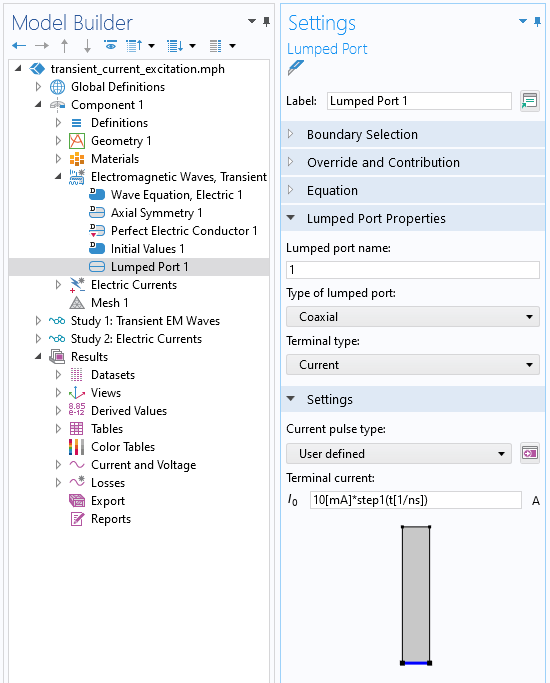
同轴类型的 集总端口边界条件屏幕截图，指定了随时间变化的电流脉冲。

我们使用同轴 类型的集总端口 边界条件，并指定一个瞬态外加电流。请注意，阶跃 函数的参数是以非维度单位输入的。总模拟时间跨度为 150ns，每 1ns 保存一次结果。下图显示了在集总端口 边界条件（在电磁波，瞬态 接口内，下图中缩写为 TEMW）处感应到的电压。曲线显示了电阻电容系统的典型响应。

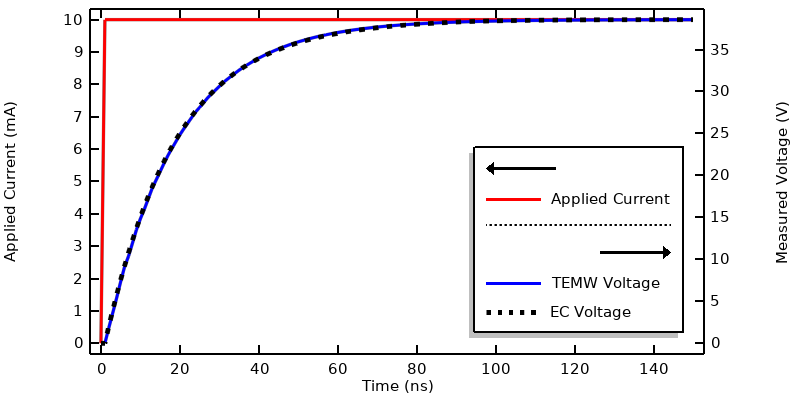
电磁波，瞬态接口和 电流接口的外加电流和测量电压图。

同样的情况也可以用电流 接口模拟，只考虑电阻和电容效应。在此接口中，电流 类型的终端 边界条件将在内部导体注入指定电流。外导体和其余外部边界均设置为接地。为了比较求解结果，将求解器的最大时步也设置为 1ns，结果显示二者非常吻合。

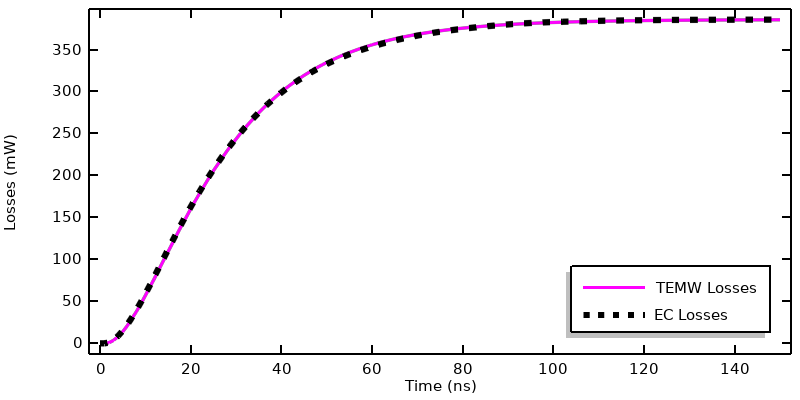
电磁波，瞬态接口和 电流接口计算出的损耗对比。

该图显示了使用两个物理场接口计算的随时间沉积到模型中的热量对比，结果显示二者非常一致。我们还可以使用 timeint() 算子计算随时间变化的集总损耗：

timeint(0,150e-9,intopSample(ec.Qh),'nointerp'),

其中，增加的 ‘nointerp’ 选项仅使用保存的时步计算体积积分的时间积分。两个接口在 0-150ns 的时间跨度内计算出的沉积能量总和为 46.8nJ，二者相差不到 1%。根据这些数据，我们可以得出结论：对于由电流信号激发的系统，电流 接口与电磁波，瞬态 接口的计算结果几乎相同，而且计算成本更低。

电流中的电压激励

接下来，让我们使用相同的阶跃函数调制电流 接口中的终端电压。也就是说，我们将尝试即时改变同轴电缆内外导体之间的外加电压。实际上这样的模型会求解失败。这并不奇怪，因为电容式设备会阻碍电压的瞬时变化。也就是说，电压的阶跃输入是非物理的。

与其尝试求解这种非物理激励，不如回到阶跃 函数并启用平滑选项。如 COMSOL 知识库中的文章：控制瞬态求解器的时间步长所述，做出这一改变后，我们就可以在 5ns 的较短时间内求解模型，每 0.01ns 保存一次结果，并将求解器相对容差严格控制在 1e-5。

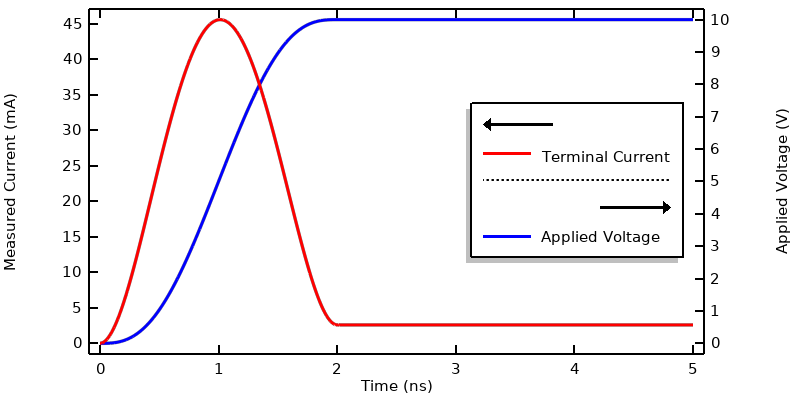
通过平滑阶跃函数计算指定电压时的电流。

该图显示了外加电压和通过终端的电流。请注意，当外加电压上升时，电流上升到稳态电流的十倍以上。为了理解这一点，我们来查看电流 接口中定义的电流表达式：

这是传导电流和位移电流之和，电场由 \mathbf{E}(t) = -\nabla V(t) 计算得出。因此，如果在边界处指定了随时间变化的电势函数，那么进入模型的传导电流和位移电流都是指定的，这是非物理的。这与前一种外加电流的情况不同，前者只指定总电流，而这个模型则计算总电流中位移电流或传导电流的比例。

我们还应该问，是否有可能在电磁波，瞬态 接口中应用类似的边界条件。这是不可能的；该接口使用的是磁矢量电势方程，不允许使用这种激励条件。即使可以通过数值方法实现，这种激励在物理上也是不可行的，因为这是一种反馈控制问题。

在时域的电流 接口中使用电压激励仍然有效，但仅限于终端边界处产生的位移电流比传导电流小得多的特定情况。也就是说，只有在设备几乎是纯电阻的情况下才使用电压边界条件。不过，我们现在研究的情况要求采用更真实的边界条件。

传输线、集总端口和终端条件

在电磁波，瞬态 接口中，让我们再来看看集总端口 边界条件。前面我们已经讨论过电流 类型，稍后将讨论电路 类型，现在我们来重点讨论电缆 类型。电缆 选项可以定义电压信号和电缆阻抗。这样就给定了一个在指定阻抗的、无限无损耗的传输线背景下理解的条件，例如 Z_0 = 50 \Omega，并在无限电缆上放置一个信号源。该信号源施加的电流会使信号沿传输线向远离信号源的两个方向传播，从而使感应电压等于所定义的信号。由于信号是双向传播的，因此外加电流的大小为 2V(t)/Z_0。

这是基于指定的电压信号 V(t) 和指定的电缆阻抗建立的——假设系统阻抗与电缆阻抗相匹配。实际上，电缆阻抗与系统阻抗（Z_s）不同，因此该信号将部分被系统模型反射并返回传输线。因此，输入信号在此边界以电压形式输入，但实际上会外加一个固定的电流以及与电缆阻抗相等的并联载荷。我们可以认为，来自电流源的信号被分成电缆和系统两部分，其中一部分信号被反射回来。在大多数真实信号源中，都会用某种循环器或隔离器来防止反射信号与电流源发生作用，并将反射信号转移到匹配的损耗载荷上。

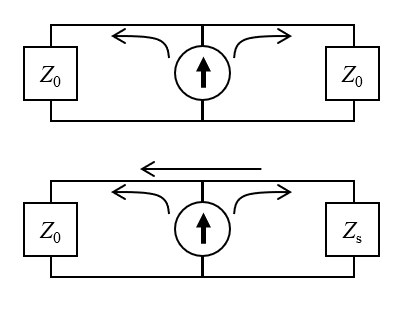
电缆类型 集总端口边界条件的等效电路解释。上图显示的是假设情况：信号从电流源传播到阻抗匹配的电缆和系统中。信号源位于电缆内，因此信号向两个方向传播。下图显示的是模拟情况：系统阻抗不匹配导致部分信号反射回电缆。

在电流 接口中，类似的边界条件是终止 类型的终端 条件。在这个接口中，我们同样可以输入电缆阻抗，但代替电压需要输入施加功率，其中功率为 \frac{1} {2}V(t)^2/Z_0。

对于这两个物理场接口，都可以使用更精细的输出时间步长和公差来求解模型。我们可以通过测量的电压、电流和损耗，以及随时间变化的集总损耗来计算结果，如下图所示。有几个特征有必要说明一下：

1. 不出意料，电磁波，瞬态 接口感应到的电压和电流信号中会出现波纹或波浪。这些波纹是由输入信号的频率组成造成的，也是由于系统模型的材料、边界条件和几何形状对信号的反射造成的。
2. 感应电压几乎是外加电压的两倍。这是因为这个边界条件也可视为电压源的诺顿等效条件，但其诺顿电阻等于电缆阻抗，在这种情况下，电缆阻抗与所模拟系统的电阻相比相对较小。
3. 使用电流 接口计算得出的解没有任何波纹，因为该接口明确忽略了电感效应，但整体形状非常相似，并给出了相同的稳态解。
4. 损耗结果非常一致，总沉积能量的吻合度在 1% 以内。

因此，我们可以得出结论，对于该系统和激励类型而言，电流 接口的计算结果非常接近于完整的电磁波，瞬态 接口计算结果。

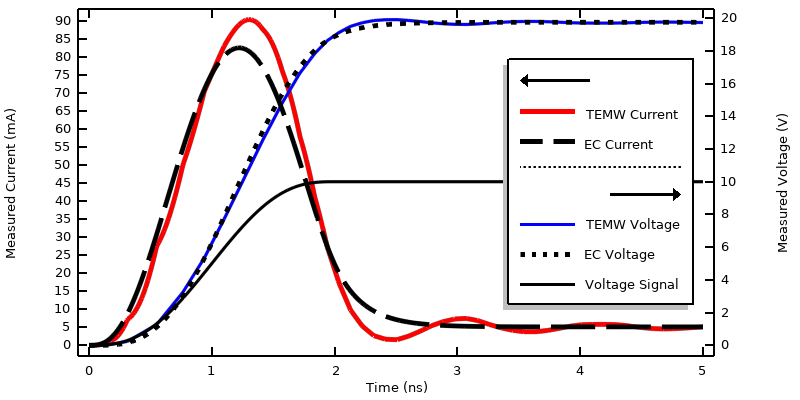
模拟沿传输线传播的外加平滑阶跃电压信号时，测量的电压和测量的电流曲线图。

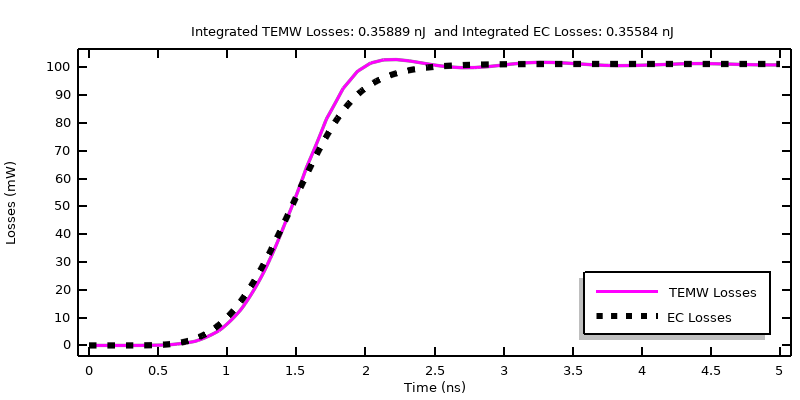
施加平滑阶跃电压信号后，计算的损耗与试验材料的损耗比较。

电路连接

从上图的电路图来看，电缆 类型的集总端口 似乎代表了连接到系统上的电阻器。我们可以使用电路 类型的集总端口，并通过电路 接口添加一个与系统并联的集总电流源和一个集总电阻器来验证这种解释。连接这些物理场接口的方法与 COMSOL 博客：了解电流仿真的激励选项中介绍的类似。通过电路 类型的终端 条件将电流 接口连接到电路 接口，可以重现相同的激励。

包括电容器、电感器和变压器等更复杂的匹配电路，也可以在电路 接口中实现。只要在电路中添加了用于防止任何类型的非物理激励的额外元件，在电路接口中使用电压源特征就是合理的。也可以包括内非线性集总器件、二极管和晶体管，但这些器件会导致方程组的计算量增大，可能需要进一步修改求解器的设置。

快速了解沉积功率

在关于电磁热系统频域激励的博客中，我们还模拟了一种将已知功率输入系统的激励。这种激励基于反馈，即监测模型的某些状态并将信息反馈给输入。在频域模型中，这种反馈是合理的，因为隐含的假设是反馈发生在几个周期内。但对于时域模型来说，该假设的合理性就大打折扣了，因为在时域模型中，任何反馈都必须包括控制系统的动态和延迟。这种时域反馈对于与我们在此研究的系统和时间跨度类似的系统并不适用。

结束语

这篇博客，我们介绍了在电流 接口和电磁波、瞬态 接口中研究用时域信号激励系统的各种方法。对于所考虑的特定系统和信号，这两个接口生成的结果非常相似。当受激系统的电能远大于磁能时，适合使用电流 接口。对于另一种情况，即系统主要是电感，磁场远大于电场时，我们将在以后的博客中单独讨论。

我们已经看到，所有激励都从根本上指定了进入系统模型的电流。电压信号沿传输线传播的情况与诺顿情况完全等同：电流源与外部电阻（代表传输线）平行于系统模型。最终，如何在代表电流源的激励选项、沿传输线传播的电压信号或添加电路 接口之间做出选择，取决于你正在处理的源类型。

这里研究的信号都很简单，但我们经常需要考虑更复杂的瞬态信号，尤其是周期性信号。这类信号适合采用一些非常有效的建模技术，我们将在下一篇文章中讨论，敬请期待！