在 COMSOL Multiphysics^® 中计算增量电感

在模拟包括线圈、非线性材料、磁体和运动部件的低频电磁系统时，经常需要计算增量电感。当线圈通过随时间变化的电流驱动时，增量电感可用于量化这类电磁系统中产生的场，而且这个量对于建立简化的集总模型尤为有用。接下来，我们将介绍在 COMSOL Multiphysics^® 软件的附加产品 AC/DC 模块中使用增量电感的理论和实践背景。

理论简述

当电路中有一条或多条导线回路时，就会涉及电感的概念，这些导线回路（或线圈）可以由一匝或多匝导线组成。假设其中一个线圈连接源，可将其称为初级线圈；如果其他线圈连接负载，则称为次级线圈。这些负载可以是其他电气设备的任意组合。

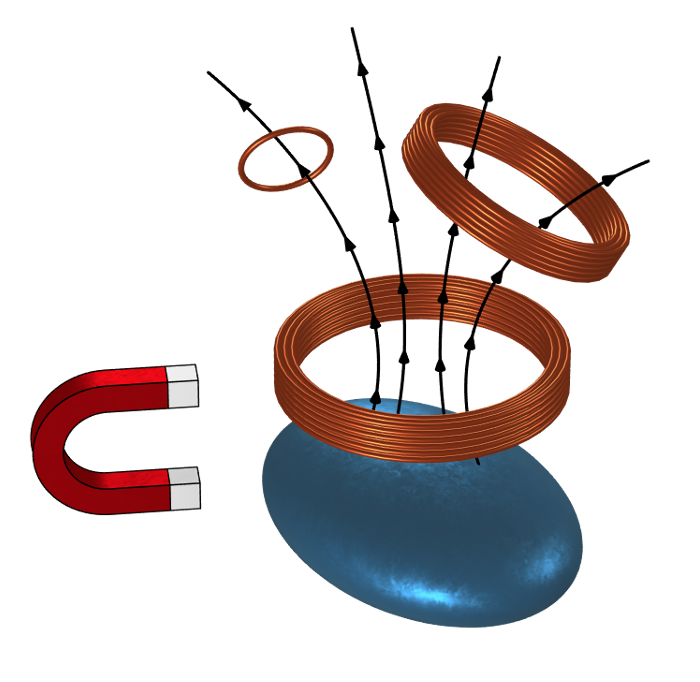
空间中的线圈、非线性磁性材料和磁体。一个线圈中的时变电流将在其他线圈中产生正比于拦截磁通量的磁场，其中偏置的非线性磁性材料将对这些拦截通量产生影响。

在线圈周围的空间中可能存在非线性磁性材料和磁体。非线性磁性材料会受到磁体、流经线圈的电流，或者在二者的共同影响下进入非线性状态。当向初级线圈施加时变电流时，包括初级线圈本身在内的所有线圈都会产生感应电动势（电压）。假设施加的信号频率远低于系统的谐振频率，就可以认为此电动势完全由时变磁场产生。基于这一假设，我们可以使用 线圈 特征进行计算。

当给定的时变电流流过第 i 个线圈时，其他第 j 个线圈的感应电动势与磁链¹的变化率成正比:

假定 \Phi 是瞬时电流的唯一函数，应用链式法则：

可以看到，感应电压为关于电流的增量电感 L’_{ij} 和施加电流的变化率 \dot{I_i} 的乘积。请注意，如果系统中的所有材料都是线性，不存在磁体，并且忽略导体中的电感损耗，那么上式可以简化为:

 
式中，L_{ij} 是视在电感，只要使用了 线圈 特征，软件就会默认计算。另一方面，计算增量电感还需要一些额外的步骤。

要理解如何计算增量电感，首先需要了解磁链。在工程类基础教材中，磁链通常被表述为：对激励线圈 \mathbf{B}_i 在表征线圈 j 的导线环表面 S_j 所产生的磁通量 \mathbf{B}_i 进行积分:

然而，如上图所示，大多数线圈的横截面积都很大，因此不可能简单地定义一个表面 S_j 。应用散度定理和 \mathbf{B=\nabla \times A }，可以通过磁矢势 \mathbf{ A } 与表征线圈中电流方向的 \mathbf{ J } 点乘后的体积分来计算 \Phi：

使用 线圈 特征时，软件会自动计算出这一数值，并将其称为线圈级联通量。

这个量可以是许多不同变量的函数，尽管我们之前假设它只是瞬时电流的函数。现在，让我们来看看如何求导数来提取增量电感。

计算增量电感

要计算增量电感，需要评估所有线圈中的线圈级联通量关于初级线圈施加电流的导数，这可以通过 灵敏度 接口实现。我们在使用 COMSOL Multiphysics^® 计算设计灵敏度的博客中介绍过这个接口，现在简要回顾一下。首先，要定义 全局目标 特征，其中需要输入线圈级联通量的表达式。还需要定义至少一个 全局控制变量 用于计算目标函数微分。然后，输入一个与流经初级线圈的直流电流相乘的变量名。通过这种设置，可以将 灵敏度 研究步骤与施加电流的 辅助扫描 相结合，计算施加电流范围内的增量电感。

在 灵敏度 接口中定义目标函数。

在 灵敏度 接口中定义控制变量。

使用 线圈 特征中的控制变量设置关于电流的微分。

在一定范围内扫描电流，同时计算灵敏度。

求解后，创建一个引用 计算组 的 插值 函数，以便在模型的其他地方使用增量电感的计算结果。

了解这些基本理论和工作流程后，现在让我们来看几个示例。

非线性电感器

首先，我们模拟了一个由合金铁氧体制成的磁芯，合金铁氧体是一种损耗极低的非线性磁性材料。磁芯从内部和外部包裹着一个线圈。我们采用了二维轴对称模型，其中线圈由 80 匝直径为 1 mm 的导线组成，工作频率为 50 Hz，因此这些导线的趋肤效应可以忽略不计，可以通过直流电阻准确预测线圈的交流电阻。在这个示例中，我们可以使用 多匝线圈域 特征在时域中求解，以获得在施加正弦电压作用下通过电感器的非正弦电流。

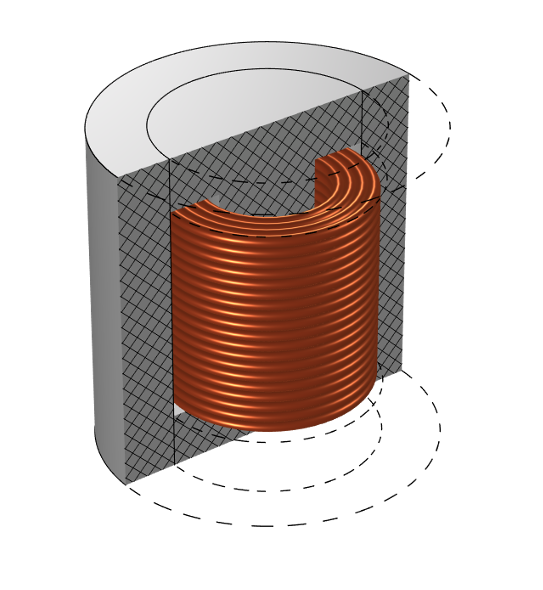
BH 非线性磁芯和环绕线圈组成的电感器。

首先，求解该模型在一定直流电流范围内的电感值，得到如下图所示的增量电感，以及用于对比的视在电感。

由非线性磁芯材料制成的电感器在一定直流电流范围内的增量电感和视在电感。

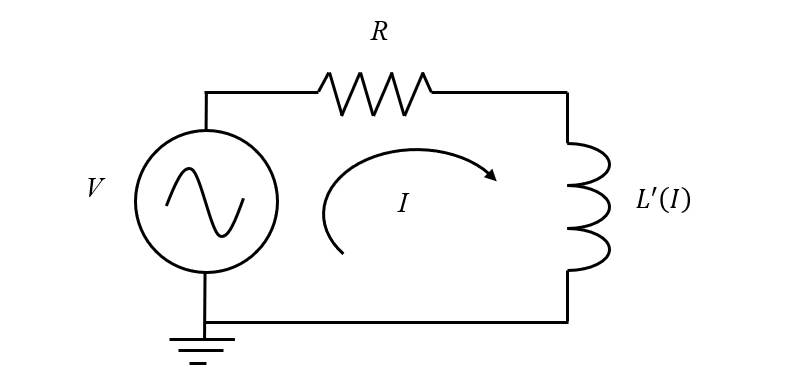
非线性电感器的等效电路模型，其中增量电感是电流的函数。

获得增量电感后，我们就可以在电路模型中使用它来快速预测瞬态行为。除了默认的 接地节点 特征外，建立电路模型只需要三个特征：

• 电阻 特征
• 电感器 特征
• 电压源 特征

使用一个 电阻 特征，阻值设置为使用 线圈 特征计算出的电阻值。在此基础上，添加一个 电感器特征，其非线性电感由存储了之前计算的增量电感的插值表定义。因为非线性特性与电流符号无关，所以可以将该非线性电感设为电流绝对值的函数。最后，将 电压源 特征串联接入。这三个特征共同创建了一个可预测响应的集总模型，将其计算结果与有限元模型的结果进行对比。请注意，在前几个周期内，结果表明仅仅只是开始接近此非线性系统的周期性稳态响应。

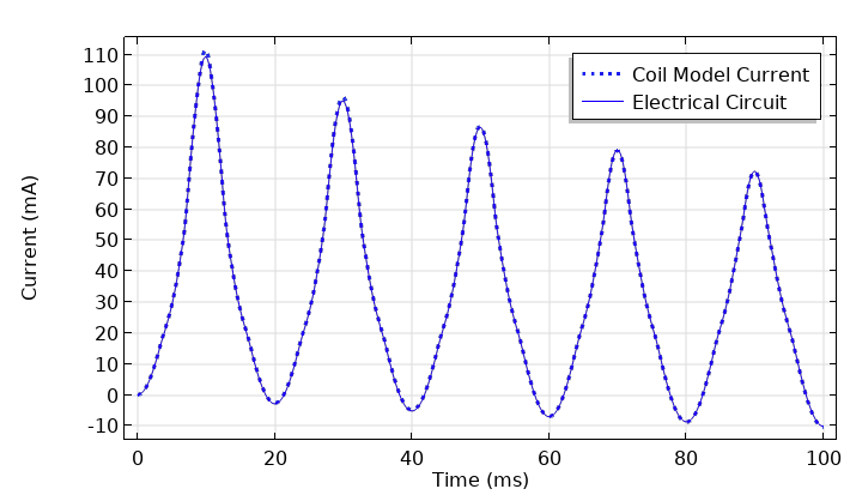
施加交流电压源时流经电感器的电流。电路模型和磁场模型的计算结果一致。

我们还可以通过傅里叶变换将这些时域数据转换到频域，以更清晰地识别由材料非线性引入的高次谐波。由于电路模型可以快速求解，我们还可以快速检查各种工作条件。不出所料，当设备进入非线性区时，会出现更多的高频分量。

电流的频谱图及其随峰值电压的变化。

含偏置磁铁的非线性电感器

为了便于说明，我们现在将上述示例进行修改，在磁芯旁边放置一块磁铁，磁铁将对线圈级联通量做出贡献，并使非线性材料发生偏置。现在，增量电感取决于施加电流的大小和符号。值得注意的是，正弦电感包含了磁铁本身对并联磁通量的贡献，但这种不随时间变化的磁通量不会对反向感应电压产生影响。磁铁只会改变系统内任一非线性材料的 B-H 关系。也就是说，磁铁不会影响仅由线性材料制成的电感器的响应。不过，必须牢记的是，磁铁始终会在正弦电感中引入偏置。因此，只要模型中存在磁铁，即使所有材料都是线性的，最好也使用增量电感。

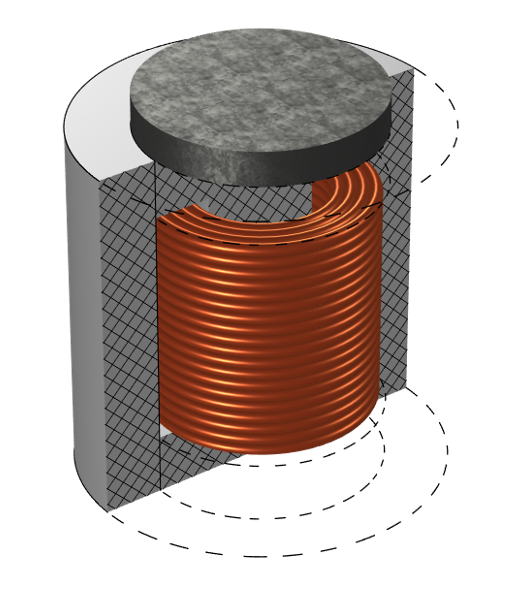
放置在 B-H 非线性磁芯顶部的磁铁会使响应偏置。

在偏置电感器中，增量电感与直流电流的符号不对称。

增量电感可再一次用于电路模型，我们再次看到，除启动期间外，二者的计算结果非常吻合。启动期间的这种不一致，凸显了用于计算空间变化场及磁芯饱和空间演变的模型与集总模型之间的差异。

空间有限元模型与包含偏置增量电感的集总电路模型的计算结果基本一致。

变压器的非线性响应

接下来，让我们来看一个由围绕合金铁氧体磁芯上的两个相同线圈组成的变压器示例。由于 L’_{11} = L’_{22} 和 L’_{12} = L’_{21}，对称性不仅可以用来减小模型大小，还可以减少计算量。一般情况下，增量电感可以是 I_1（初级电流）和 I_2（次级电流）的函数，但对于这种对称结构，L'(I_1,I_2) = L'(|I_1+I_2|,0) ，我们只需要计算增量电感 L’_{11} 和 L’_{12}；保持 I_2=0 的情况下，在 I_1 的范围内计算，无需对两个变量进行扫描。

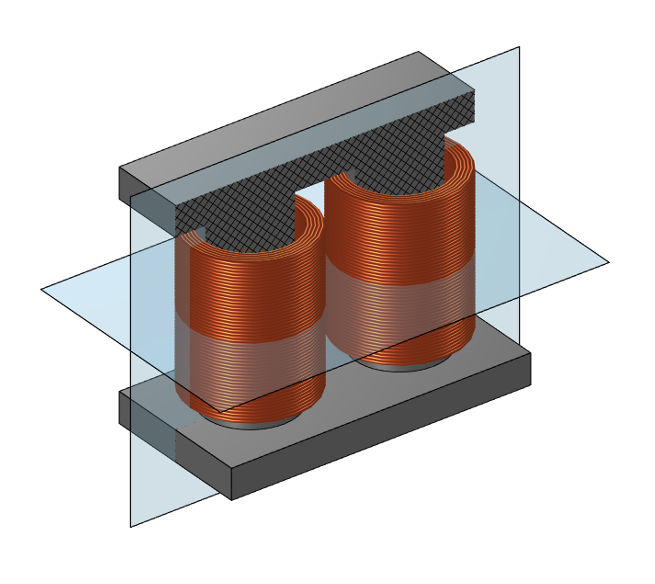
由围绕在对称磁芯上的两个相同线圈组成的变压器，图中可以看到两个对称平面。

计算出这两个增量电感后，就可以使用一组函数来定义互感矩阵的所有四个项。这些项可以在同一变压器的电路模型中使用。由于存在非线性，两个线圈之间的耦合通过 电流控制的电压源 特征模拟，如下图所示。

含非线性磁芯的变压器等效电路。

使用完整的三维模型求解该变压器的响应需要大量的计算成本，而使用电路模型求解则非常快速。尽管在所有可能的运行工况下计算增量电感矩阵非常重要，但我们最终得到的结果还是非常吻合。为了提高计算效率，可以通过 批处理 或集群扫描 的并行方式一次性计算所有工况，以充分利用所有可用的计算资源。

施加在初级线圈上的正弦交流电压会在初级线圈和次级线圈上产生非线性电流。使用完整的三维模型和电路模型求解的初级线圈上的电压和次级线圈上的电流的对比。

螺线管线圈的动态响应

现在，让我们来看一个由铁质外壳内的线圈和铁质柱塞组成的螺线管。柱塞的安装方式使其只能沿其轴线移动。假设铁的磁导率在预期磁场范围内保持不变，并忽略材料的非线性。同时假设外壳和柱塞是绝缘材料，能将绕轴线的所有感应电流降至最低，因此可以将铁芯视为无损耗材料。

由铁制外壳内的线圈和由弹簧固定的铁柱塞组成的螺线管线圈。

弹簧将柱塞固定在壳外的位置以保持平衡。当向线圈施加电压时，电流开始流动，并推动柱塞向中心移动。在这种情况下，不存在材料非线性，因此级联通量与瞬态电流 I 呈线性关系，但与柱塞的 z 向位置 u 呈非线性变化：

因此，根据链式法则，反向感应电压为：

式中第一项考虑到了视在电感随柱塞位置变化这一事实。当柱塞在非零磁场中以速度 \dot{u} 运动时，第二项引入了一个额外的反向感应电压。

考虑到级联通量与施加的直流电流（I_{DC} ）呈线性关系，第一个方程对位置进行微分得到：

因此，为了计算关于位置的导数，结合使用 灵敏度 接口与 动网格 接口，在保持直流电流不变的情况下，计算级联通量关于 z 位置无限小变化 \delta 的偏导数：

我们通过 动网格 接口引入了 z 向位置的有限和无限小变化，然后对无限小位移（\delta）求偏导，并沿柱塞行程的一系列不同位置（u）进行扫描。通过偏导结果，现在可以建立一个简单的机电集总模型，将电路模型与柱塞运动方程结合起来。

机电集总模型由一个电路模型和一个集总机械模型组成，其中集总机械模型由柱塞运动时的力、与位置相关的视在电感和反向感应电压耦合。

由集总系统的示意图可以看到，电气系统通过力与机械系统耦合。要理解力的表达式是如何得出的，让我们先来看看系统中随电流和柱塞位置变化的总磁能的表达式：

柱塞上的总力可以通过虚功方法求得，对于线性磁性材料，轴向力可以通过总磁能关于无限小位移的偏导数求得：

也就是说，力是通过线圈的电流和电感关于位置的偏导数的函数，这一点我们已经计算过了。因此，在模拟螺线管的同时，我们还要求解柱塞位置的常微分方程：

式中，u_0 是柱塞的平衡位置。这个方程可以通过 全局常微分方程和微分代数方程 接口或可添加到任何物理场接口的 全局方程 特征来求解。因此，该方程可以与 磁场 接口耦合来求解运动，还可以与 电路 接口耦合进行求解。

我们将使柱塞沿轴线自由振荡，并根据一组输入的结果来研究其产生的一些动态过程，目的是说明集总模型与用于计算集总参数的空间模型的计算结果非常吻合。

螺线管磁场的精确模型与集总模型的计算结果对比。

尝试建立集总模型

这篇文章，我们通过 4 个示例重点展示了 COMSOL Multiphysics^® 软件不仅可以提取增量电感，还可以计算线圈级联通量关于其他输入变量的导数。由此得到的量可用于构建简化的集总模型，从而准确预测系统的性能。

想尝试自己动手计算增量电感并建立这类集总模型吗？请点击按钮，进入 COMSOL 案例库，下载文中的示例模型：

参考文献

1. 1. D. Cheng, “Field and Wave Electromagnetics”, 2nd ed., Addison-Wesley, 1991