
波士顿今年的冬天非常暖和,不过我们最终还是迎来了今年的首场降雪。刚刚凝视窗外时,我不禁想到了雪花,然后又想起我们很难用数学描述它们的形成。不过,有种雪花是个例外,我们可以轻松对其进行描述,这就是科赫雪花。现在,我们将讨论如何用 COMSOL Multiphysics 的 App 开发器来创建这一形状。
创建科赫雪花
正如我们在之前博客中所讨论的,分形有一些非常有趣的工程应用。科赫雪花就是一种著名的分形,它的迭代构造方法非常简单:
- 从一个等边三角形开始,这其实就是科赫雪花的零次迭代。
- 找到当前雪花中每条边的中心点。
- 在每条边的中心点增加一个向外的等边三角形,边长是当前每边长的 1/3。
- 定义科赫雪花的下一次迭代,在之前雪花的外边及所有新增三角形的外边进行迭代。
- 重复步骤 2-4,进行尽可能多的迭代。
下图显示了雪花的前 4 次迭代。
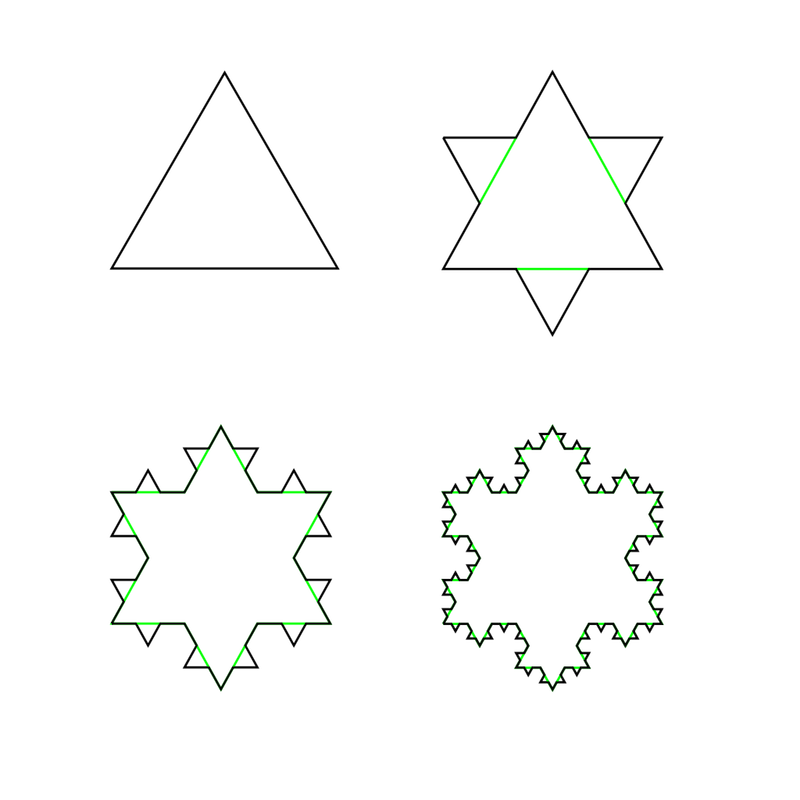
科赫雪花的前四次迭代。图片为 Wxs 自行制作。已获 CC BY-SA 3.0 授权,并通过 Wikimedia Commons 分享。
构建科赫雪花的几何结构
既然已经掌握了所用算法,我们现在将利用 COMSOL Multiphysics 及 App 开发器来创建这类结构。新建一个文件,在全局定义节点下创建一个二维几何零件。该零件包含五个输入项:等边三角形的边长;底边中心点的 x 及 y 坐标;以及如下图所示,从底边中心点指向顶点的法向矢量的分量。
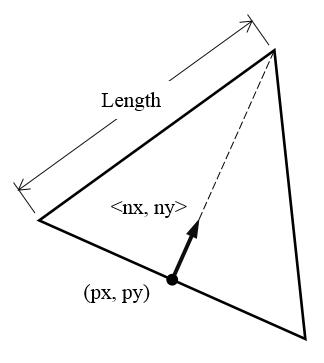
这五个参数用来定义等边三角形的大小、位置及取向。
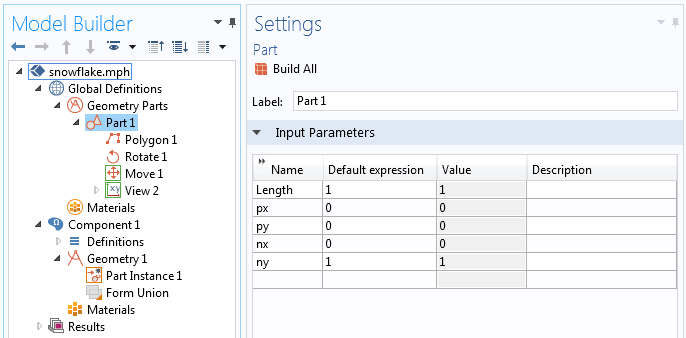
定义几何零件的输入参数。
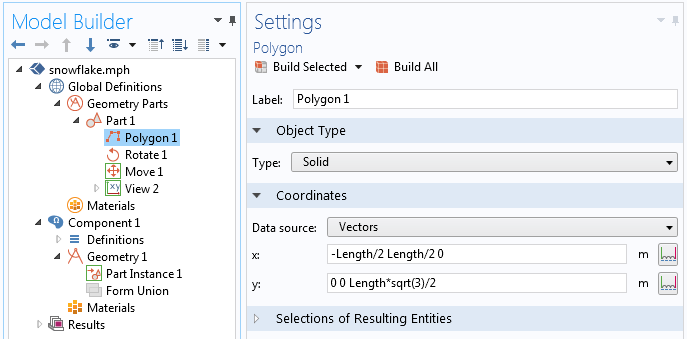
用于定义等边三角形的多边形基元。
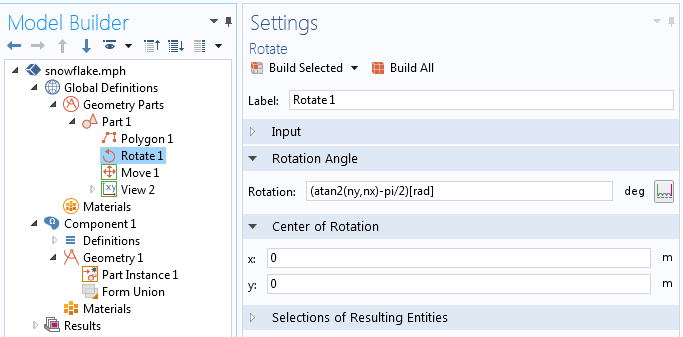
将零件绕底边中心旋转。
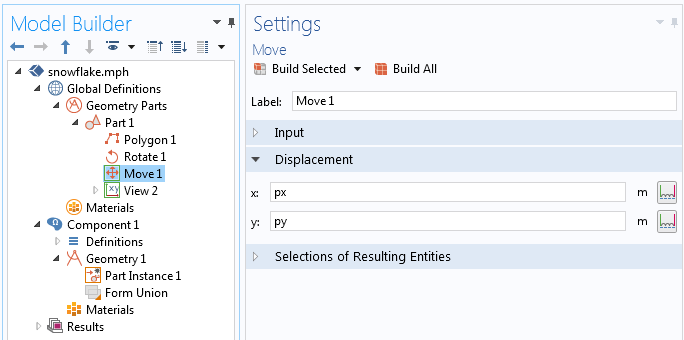
移动零件的位置。
定义几何零件后,我们可以在几何分支下调用零件的单个实例。最初的三角形相当于科赫雪花的零次迭代,我们现在可以开始使用 App 开发器来创建更复杂的雪花。
在 App 开发器内布置 App 的用户界面
科赫雪花 App 的用户界面非常简单,只包含两个可与用户交互的特征:滑块(下图中标为 1)指定了绘制雪花的迭代次数;按钮(2)用于绘制及展示生成的几何。此外,还包括一个文本标签(3)和一个数据显示(4),用于显示进行的迭代次数;最后,还有一个图形窗口(5),用于绘制生成的几何。
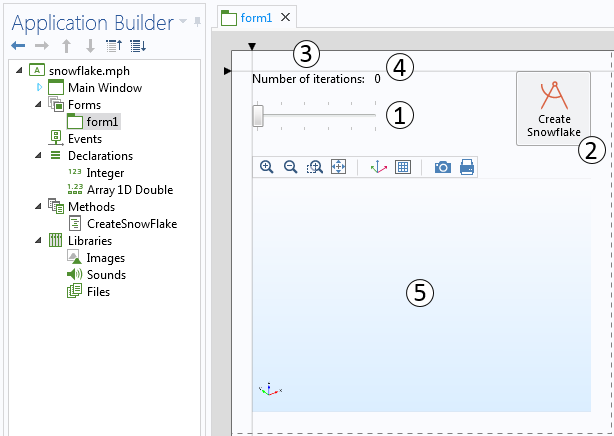
App 内包含一个表单,表单内含五项特征。
此外,App 中还包含两项声明,用于定义一个名为Iterations的整数值,缺省为零,允许用户修改;还包括一个一维双精度数组,称为 Center。阵列内单个单元的值为 0.5,用于找到每边的中心点。这个值始终不变。
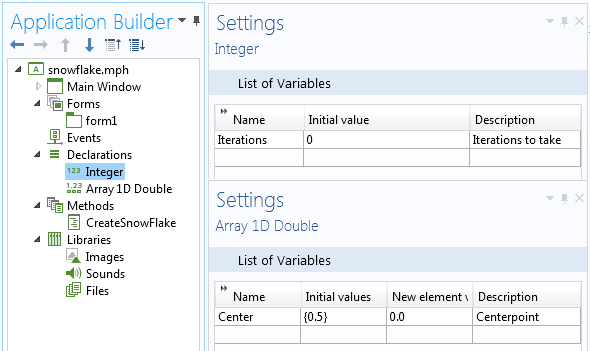
两项声明的设定。
用户界面内的滑块特征控制了 Iterations 的整数值。下图显示了滑块设定及值,指定为 0 到 5 之间的整数。源的选择类似于数据显示特征,用于显示迭代次数。由于我们选了一个较易执行但执行效率并非最高的算法,所以限制用户可以执行五次迭代。
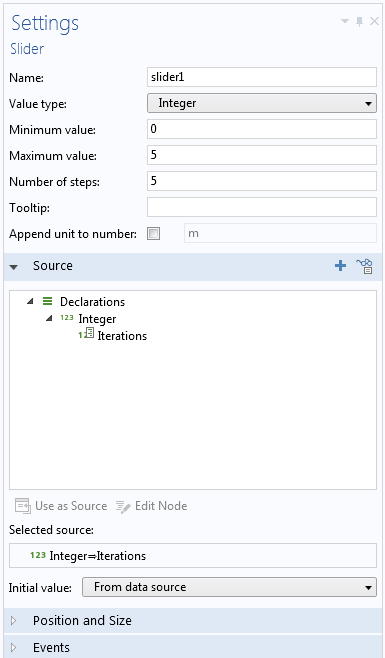
滑块特征的设定。
接下来,我们可以查看按钮的设定,如下图所示。点击按钮将运行两个命令。首先,调用 CreateSnowFlake 方法。之后,产生的几何将绘制在图形窗口中。
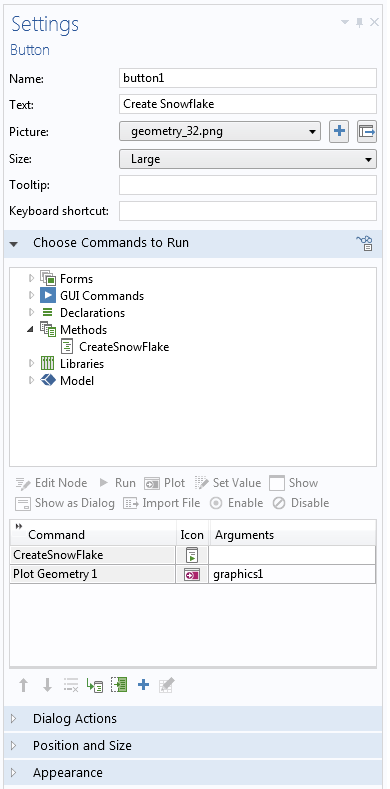
按钮设定。
我们已经察看了 App 的用户界面,并从中了解到雪花几何的创建需要在方法内实现。我们将再分析方法内的代码,左侧为行号,右侧用红色突出显示了文本字符串:
1 model.geom("geom1").feature().clear(); 2 model.geom("geom1").create("pi1", "PartInstance"); 3 model.geom("geom1").run("fin"); 4 for (int iter = 1; iter <= Iterations; iter++) { 5 String[] UnionList = new String[model.geom("geom1").getNEdges()+1]; 6 UnionList[0] = "pi" + iter; 7 for (int edge = 1; edge <= model.geom("geom1").getNEdges(); edge++) { 8 String newPartInstance = "pi" + iter + edge; 9 model.geom("geom1").create(newPartInstance, "PartInstance").set("part", "part1"); 10 with(model.geom("geom1").feature(newPartInstance)); 11 setEntry("inputexpr", "Length", toString(Math.pow(1.0/3.0, iter))); 12 setEntry("inputexpr", "px", model.geom("geom1").edgeX(edge, Center)[0][0]); 13 setEntry("inputexpr", "py", model.geom("geom1").edgeX(edge, Center)[0][1]); 14 setEntry("inputexpr", "nx", model.geom("geom1").edgeNormal(edge, Center)[0][0]); 15 setEntry("inputexpr", "ny", model.geom("geom1").edgeNormal(edge, Center)[0][1]); 16 endwith(); 17 UnionList[edge] = newPartInstance; 18 } 19 model.geom("geom1").create("pi"+(iter+1), "Union").selection("input").set(UnionList); 20 model.geom("geom1").feature("pi"+(iter+1)).set("intbnd", "off"); 21 model.geom("geom1").run("fin"); 22 }
我们来分析每行代码的作用
- 清除所有几何序列,以便重新开始绘制。
- 使用缺省尺寸、取向及位置创建一个简单的三角形零件实例。这就是雪花的第零阶,标签标识符为
pi1。 - 完成几何。这是重置所有几何指标的必须操作。
- 根据指定的雪花迭代次数开始迭代,使用声明中的
Iterations作为停止条件。 - 定义一个空的字符串阵列
UnionList。阵列中的每个单元均包含对应于不同几何对象的标签标识符。阵列的长度等于最后一次迭代的边数 + 1。 - 定义
UnionList阵列中的第一个单元。这是前一步迭代结果的标签标识符。请记住:我们已经在第 1-3 行创建了零次迭代。iter的整数值会自动转化为一个字符串,并附于字符串"pi"。 - 按之前创建的雪花的边数执行迭代。
- 指定在此边上创建的新三角形零件实例的标签标识符。注意
iter及edge的整数值会按顺序附于字符串pi,即零件实例的标签标识符。 - 创建一个三角形零件实例,并给与其刚刚指定的标签标识符。
- 使用
with()/endwith()语句指定行 11-15 指向当前零件实例。 - 指定侧边三角形的长度。零阶的边长为 1,因此第 n 次迭代的边长为 (1/3)n。需要
toString()函数来将浮点值转换成字符串。 - 将新三角形的 x 位置指定为最后一次迭代时侧边的中点。
edgeX方法已收录在《COMSOL 编程参考手册》中。请回想我们将Center设为 0.5。 - 指定 y 位置。
- 指定三角形法向矢量的 x 分量。
edgeNormal方法已收录在《COMSOL 编程参考手册》中。 - 指定法向矢量的 y 分量。
- 结束
with()/endwith()语句。 - 将当前三角的标签标识符增加到所有对象列表中。
- 结束在所有边上的迭代。
- 针对几何序列中的所有对象执行一次布尔并集运算。指定标签为
piN,其中N是下一次的迭代次数。需要在(iter+1)前后加括号,以便将iter的增量值转换为字符串。 - 指定最后一个未保存对象的内边界。
- 完成几何。这将为下一次几何迭代重置所有几何指标。
- 完成雪花创建的迭代循环。
至此,我们已经介绍了 App 中的各个方面。我们来看下结果!
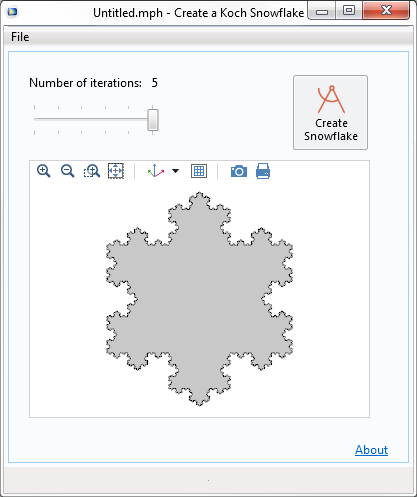
我们的简单科赫雪花 App。
我们可以进一步拓展 App,将几何写成一个文件,甚至直接在其中执行其他分析。例如,我们可以设计分形天线。如果您对天线设计感兴趣,不妨看一下我们的Sierpinski 分形单极天线模型,甚至可以尝试从头创建模型。
自己动手操作:
如果您希望自行开发 App,或是还没用过 App 开发器,以下资料将对您非常有帮助:
- 下载《App 开发器简介》
- 观看视频教程,学习如何使用App 开发器和 COMSOL Server™
- 阅读博客,了解如何在各应用领域使用仿真 App
读完这些材料后,您将掌握如何对 App 进行拓展,从而能更改雪花尺寸、导出创建的几何,以及计算面积及周长。
您希望用 COMSOL Multiphysics 创建哪类 App 呢?如果您有任何疑问,欢迎随时与我们联系。



评论 (3)
红斌 徐
2017-03-05cool
Feiyan You
2023-04-09Could you send the original mph file to me,please? Because,when i was making the model ,the result can not be the same as the example,so,i hope you can send the example to me to help find out the question.
Thank you very much for your reading! looking forward to your reply!
Min Yuan
2023-04-10 COMSOL 员工We recommend that you email the support system to obtain the model :http://cn.comsol.com/support