使用布辛涅斯克近似模拟自然对流

今天，我们将比较的 布辛涅斯克近似 与完整 纳维-斯托克斯方程 在自然对流问题中的应用。本文介绍了如何在 COMSOL Multiphysics 软件中实现布辛涅斯克近似，以及使用布辛涅斯克近似的潜在优势。

应用示例：方形空腔中的自然对流

在下面的示例中，我们将使用一个耦合了纳维-斯托克斯方程和传热方程的模型来模拟带有加热壁的方形空腔中的自然对流。空腔左壁和右壁的温度分别为 293K 和 294K；顶壁和底壁是隔热的；流体是空气，侧面的长度为 10cm。

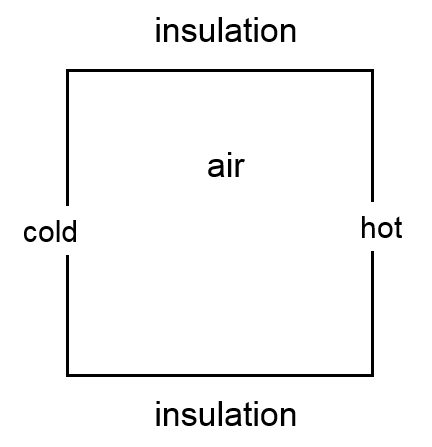
我们将使用此模型比较三种不同建模方法的计算成本：

1. 求解完整的纳维-斯托克斯方程（方法1）

 

\rho \left( \frac{\partial \mathbf{u}}
{\partial t} + \mathbf{u} \cdot \nabla \mathbf{u} \right) = -\nabla p + \nabla \cdot ( \mu (\nabla \mathbf{u} + (\nabla \mathbf{u})^{T}) -\frac{2}{3} \mu (\nabla \cdot \mathbf{u})\mathbf{I}) + \rho \mathbf{g}

 

2. 用压力变换求解完整的纳维-斯托克斯方程（方法2）

 

\rho \left( \frac{\partial \mathbf{u}}{\partial t}
+ \mathbf{u} \cdot \nabla \mathbf{u}\right) = -\nabla P + \nabla \cdot ( \mu (\nabla \mathbf{u} + (\nabla \mathbf{u})^{T})- \frac{2} {3}\mu (\nabla \cdot \mathbf{u})\mathbf{I}) + (\rho-\rho_0)\mathbf{g}

 

3. 使用带压力变换的布辛涅斯克近似（方法3）

 

\rho_{0} \left( \frac{\partial \mathbf{u}}{\partial t} + \mathbf{u}\cdot \nabla \mathbf{u} \right) = -\nabla P + \mu \nabla^2 \mathbf{u}-\rho_0\frac{T-T_0}{T_0}\,\mathbf{g}

 

在COMSOL 多物理场仿真百科中，我们介绍了这三种方法及其变量的定义。

我们使用 COMSOL Multiphysics 中的层流、流体传热 接口、非等温流多物理场耦合进行静态研究来求解模型：

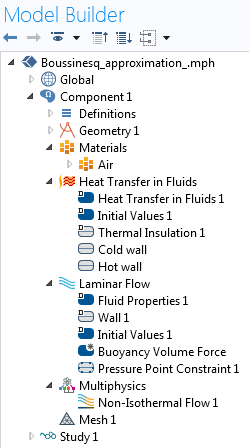
在建立模型时，检查流动是层流还是湍流很重要。对于自然对流问题，我们是通过计算格拉斯霍夫数来实现的。对于理想气体，我们可以定义为
 

 
格拉斯霍夫数是浮力与黏性力之比。当格拉斯霍夫数低于 10^8 时表示流动为层流，而高于 10^9 时表示流动为湍流。在本文中，格拉斯霍夫数为 1.5 \times \hspace{1pt} 10^5 左右，说明流动是层流。

方法 1

使用完整的纳维-斯托克斯方程时，将浮力设置为 \rho \mathbf{g} ：

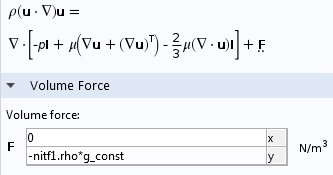
使用体积力功能添加浮力项。术语 nitf1.rho 和 g_const 分别代表与温度和压力相关的密度 \rho，以及重力加速度  \mathbf{g}。

方法 2

当使用带压力变换的纳维-斯托克斯方程时，我们必须进行三个更改。

首先，需要将体积力的定义更改为 (\rho-\rho_0)\mathbf{g}，例如：

术语 rho0 是指参考密度 \rho_0。

接下来，用变量表中的材料属性计算参考密度 \rho_0 和参考黏度 \mu ：

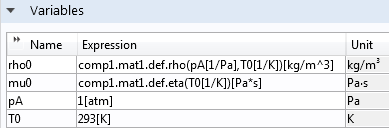
其中，pA 和 T0 分别代表参考温度和压力。

空气黏度被设定为常数 \mu_{0} ：

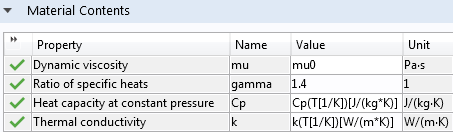
方法 3

最后，当使用布辛涅斯克近似时，需要将浮力设置为 -\rho_0\frac{T-T_0} {T_0}\,\mathbf{g}

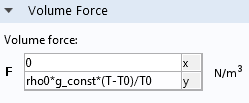
与方法2 一样，我们还需要根据材料属性计算参考密度和黏度。方法3 的第三步也是最后一个步骤，是将流体密度设置为恒定的参考密度 \rho_{0} (布辛涅斯克近似认为，除了在浮力项中以外，密度是恒定的)。

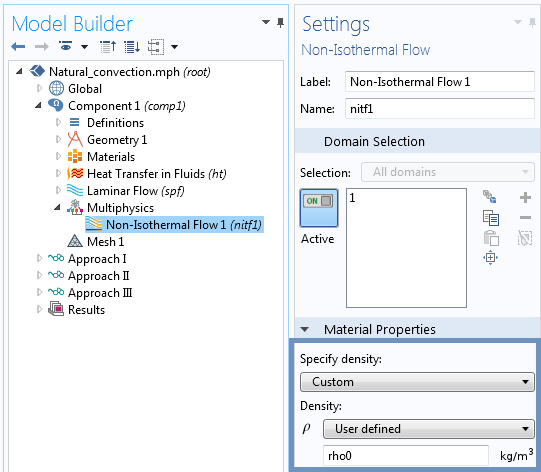
注意：如果模型包含压力边界条件（开放域），则将方法1 的压力设置为静水压力 -rho0 * g_const * y，将方法2 和方法3 的压力设置为 0 [Pa]。COMSOL 案例库中有一个包含重力的模型边界条件示例。

该网格是由 15000 个三角形单元和 1200 个边界层单元组成的。他们都是一阶单元。

结果

以上三种方法得出的速度大小和流线几乎相同。方法1 和方法2 之间的最大温差小于 2 \times \hspace{1pt} 10^{-6} K，方法1 和方法3 之间的最大温差约为 5 \times \hspace{1pt}10^{-4} K，唯一不同的是仿真时间。

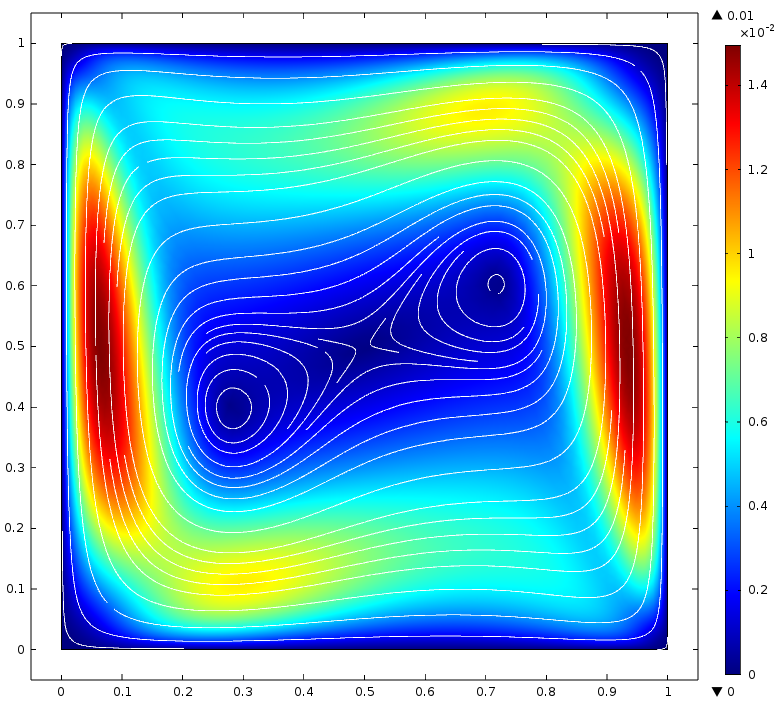
速度大小和流线。

由于此二维仿真的运行时间很短（大约 30s），我们通过比较求解器从收敛到稳态解所需的迭代次数来查看计算负载。在这种情况下，迭代次数几乎与 CPU 时间成正比。

下表比较了三种方法的迭代次数。

这些结果非常令人惊讶！

虽然布辛涅斯克近似可减少模型的非线性和收敛所需的迭代次数，但完整的纳维-斯托克斯方程（39 个迭代）的求解速度仍然快于布辛涅斯克近似（55 个迭代）。我们还注意到，使用带有压力转换的纳维-斯托克斯方程可产生与布辛涅斯克近似相同的迭代次数。

为了更好地理解这些结果，我们可以在禁用伪时间步进算法之后运行第二组仿真。伪时间步进用于稳定传递问题中向稳态的收敛。伪时间步进依赖于自适应反馈调节器来控制一个柯朗-弗里德里希斯-列维条件（CFL）数。伪时间步进通常是模型收敛的必要条件。但是，在本次特定的情况下，则不需要。

以下是 COMSOL Multiphysics 中带有伪时间步进的默认求解器设置的设置窗口：

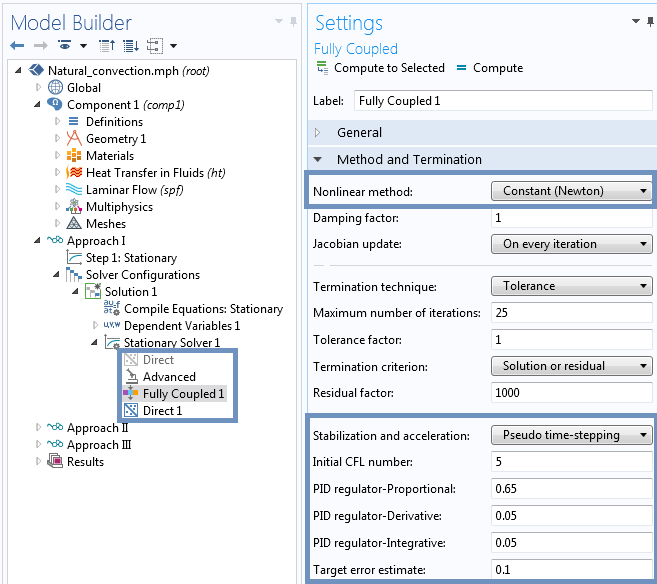
以下快照显示了没有伪时间步进的更新的 求解器设置。除非可以轻松调整求解器设置，否则我们建议始终保持开启伪时间步进。

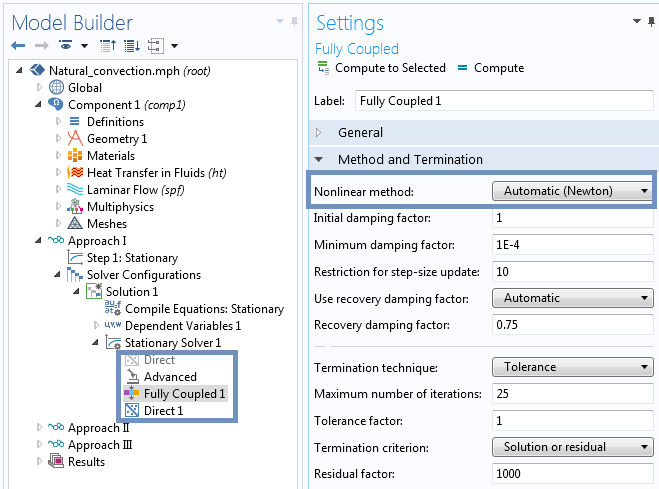
请注意自然对流的求解器设置：

由于在自然对流建模中层流与传热物理场之间存在非常强的耦合，因此请始终使用完全耦合求解器。在层流物理场中添加体积力时，COMSOL 软件会自动切换到完全耦合求解器，这意味着我们正在模拟自然对流。

下表显示了没有伪时间步进的迭代次数：

这些结果比之前使用伪时间步进时的结果更有意义。这是因为最线性问题的方法3 的收敛速度比方法1 快。令人惊讶的是，方法2 和方法3 收敛的迭代次数相同。

将这些结果与第一组结果进行比较，发现第三种方法（布辛涅斯克近似）的速度加速了 8 倍（从 55 到 7 次迭代）。这些结果还表明，第一组结果中的迭代次数不仅取决于问题的线性程度，还取决于伪时间步进算法的调整。

我们学到了什么？

在这里，我们讨论了如何实施布辛涅斯克近似及其优点，以及如何使用压力转换方法。结果表明，对于该特定模型，无论是否启用伪时间步进，在计算时间上使用布辛涅斯克近似都没有实际用处。这通常是因为布辛涅斯克近似仅在非线性较小时才有效。相对于完整的纳维-斯托克斯方程，当布辛涅斯克近似的计算时间短得多时，这表明布辛涅斯克近似可能无效。

由于使用布辛涅斯克近似法计算加速较小，并且事实上并不容易知道布辛涅斯克近似法是否有效，因此我们通常建议求解完整的纳维-斯托克斯方程。但是，实施压力变换（方法2 和 3）确实避免了舍入误差，并简化了瞬态问题以及具有开放边界的模型的实施。这将是下一篇博客文章的研究目标。

与方法2（带压力变化的纳维-斯托克斯方程）相比，使用包含更多的实施步骤的方法3（带压力变化的布辛涅斯克近似）并不会减少迭代次数。方法3 的最终仿真时间可能会稍短，因为它不需要计算与温度和压力相关的密度以及与温度相关的黏度，但这种加速可能并不明显。

通过禁用伪时间步进算法，迭代次数根据所选方法的不同会减少4到8倍。但是请记住，如果没有伪时间步进或其他负载渐变或非线性渐变策略，大多数问题将不会收敛。

您可以使用CFD 模块或传热模块来设置和求解该模型。如果您对我在本篇博客文章中介绍的模型有任何疑问，请联系我们的技术支持团队。如果您还不是 COMSOL Multiphysics 用户，并且想进一步了解我们的软件，请通过此表格与我们联系 – 我们将很乐意与您联系。