在非等温流动仿真中使用流入边界条件

模拟非等温流动时需要同时进行计算流体力学（CFD）和传热分析。如果入口处的流体温度已知，我们可以使用 温度 边界条件。但是，在一些重要的情况下，却并非如此。这时我们就需要用到 流入 边界条件，它可以提高模型精度，降低仿真计算成本。今天，我们讨论如何在流动入口设置这个复杂的热边界条件。

使用流入边界条件模拟传热

这里我们讨论的重要边界条件叫做 流入 边界条件。它可以在流体域外部的边界处使用，相当于在“上游”有一个虚拟通道。流入 边界条件用于定义入口边界处的热通量，该热通量就像将虚拟通道建模为真实的计算流体力学域一样为流体域带来相同的能量。虚拟通道可以看作是一个长的绝热通道，在入口处具有给定的热特性，并且具有与 流入 边界条件设置中定义相同的速度分布。

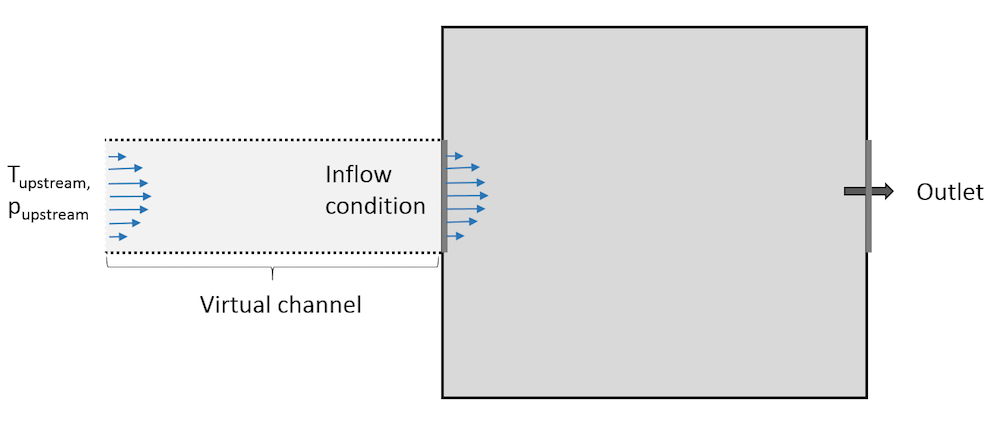
对应于流入边界条件的虚拟域的示意图。

在数学上，边界条件使用通量条件来表述:

(1)

 
其中，焓变 \Delta H 定义为:

(2)

这里，我们可以定义两个项:

和

焓变公式可以写为:

这个表达式包含两个项。首先，{\Delta H}_T 取决于温差，其次，{\Delta H}_p 取决于压差。

等式(1) 表示法向传导热通量(-\mathbf{n} \cdot \mathbf{q}= k\nabla T \cdot \bf{n})在流入边界与上游条件和入口条件之间的流速和焓变成正比。

流入边界条件的温度贡献

如等式(2) 所示，焓变一般取决于温度差和压力差。然而，当压力变化引起的功不包括在能量方程中时，压力对焓的贡献 {\Delta H}_p 忽略不计。

在 COMSOL Multiphysics 软件中，这可以通过非等温流动 多物理场特征中相应的复选框来控制:

还有一种典型的情况，当流体被模拟成理想气体时，这个项被抵消了。事实上，在这种情况下，\alpha_p = \frac{1}{T}。

首先，我们假设压力对焓的贡献为零。(我们在上面已经看到，这实际上是很常见的情况。) 然后，边界条件为:

(3)

当对流传热在进口处占主导地位时(大流量)，温度梯度以及沿进口边界法线方向的传导热传递非常小。所以在这种情况下，等式(3) 强制焓变接近于零。由于 C_p 是正的，所以 流入 边界条件需要满足 T = T_{\mathrm{upstream}}。所以，当对流传热在入口处占主导地位时，流入 边界条件几乎等同于描述入口上游温度边界条件的狄利克雷 边界条件。

相反，当流速较低或入口附近存在大的热源或散热器时，传导热通量不能忽略。此外，必须调整入口温度，以平衡入口流动带来的能量和内部传导传递的能量，如等式(3) 所述。

从而能观察到由入口周围的热传导对上游温度的影响。

比较流入边界条件和 Danckwerts（法向通量）边界条件

假设焓只取决于温度，并且热容量是恒定的，等式(1) 可以写作:

(4)

这与在稀释质传递 接口中使用的 Danckwerts 边界条件一致。

实际上，有许多模型中热容基本为常数，所以使用 流入 边界条件类似于 Danckwerts 平均热容量的边界条件。有趣的是，如果不是这样，那么 流入 边界条件自动考虑了对应于焓的变化导致的输入通量变化，那么就不能简单地用 Danckwerts 界条件。

流入边界条件的压力贡献

我们来讨论一个一般情况下的案例。在等式(2) 中，焓的变化取决于温度差和压力差。

考虑到 流入 边界条件时等效于添加了一个输入进气道的虚拟通道，我们希望在虚拟通道进气道和边界之间的压力损失被定义。这解释了为什么上游压力与入口压力不同。当流体流过通道时，采用流入条件的边界受到压力功的影响，导致虚拟通道入口和边界之间的温度变化。这就是等式(2) 中由压力相关项所描述的项。请注意，虚拟通道中的黏性耗散没有考虑在内。

在实际情况下，压力贡献 {\Delta H}_p，通常为零(对于理想气体或忽略压力变化做功时)或很小，因为上游温度和流入温度之间非常小的差异就足以平衡它。为了说明这一点，考虑两种常见的流体:

1. 空气:它的密度是由材料库中的理想气体定律定义的，因此压力对焓的贡献
   {\Delta H}_p 为零。
2. 水: C_p 的数量级为 1000J/K/kg，而 \frac{1- \alpha_p T} {\rho} 的数量级是 0.001m³/kg。1bar(= 10⁵Pa) 的压差和 0.1K 温度差分别得到{\Delta H}_T \sim 0.1 \mathrm{K} \times 1000 \mathrm{J/K/kg} = 100 \mathrm{J/kg} 和 {\Delta H}
   _p \sim 0.001\mathrm{m^3/kg}\times 10^5\mathrm{Pa}= 100\mathrm{J/kg}，这两个因素对 \Delta H 大小变化的贡献在数量级上相同。

流入和温度边界条件比较

为了说明 流入 边界条件与温度 边界条件，我们可以研究二维长通道中的稳定温度分布，它实际上代表两个板块之间的流动。超过某个点后，通道被两侧的对流热通量冷却。通道高度为 1cm，采用对流热通量的部分长度为 10cm。通道内充满空气(密度遵循理想气体定律)。

在离冷却区一定距离的入口处，平均速度为温度为 U_in，温度为 30℃。对流热通量可以定义为 h(T_cold-T)，其中 h=100 W/m²/K,T_cold=10℃。

大多数温度变化发生在施加热通量的点之外，因此我们可以选择通过仅模拟冷却区域之前的一部分通道来减少计算区域。下图包含两个草图。底部的图有一段长度 L_inlet=2cm 的冷却区域，而在顶部，入口与冷却区域的起点重合(L_input=0).

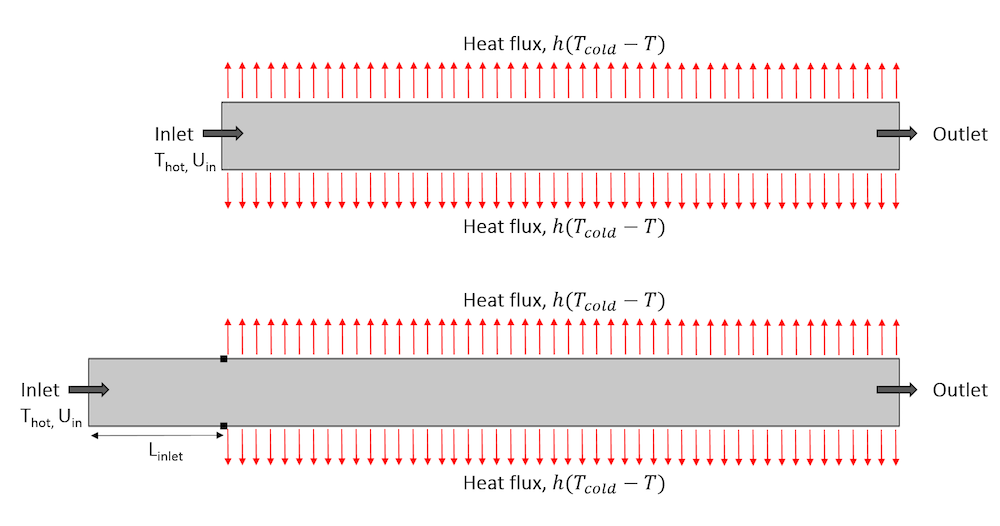
暴露于热通量区域之前的截面(顶部)和暴露于热通量区域开始处的入口(底部)的几何图形。

现在我们使用温度 或者流入 入口处的边界条件来求解模型。我们改变了在模型中的两个参数:

1. 入口速度，U_in: 1cm/s 和 10cm/s

1. 暴露于热通量区域之前的通道长度，L_inlet:0, 0.2, 1, 和 2cm

这些模拟的目标是确定 L_inlet，我们可以使用温度 和流入 边界条件分别设置精确的热边界条件。

最高入口速度的模拟结果

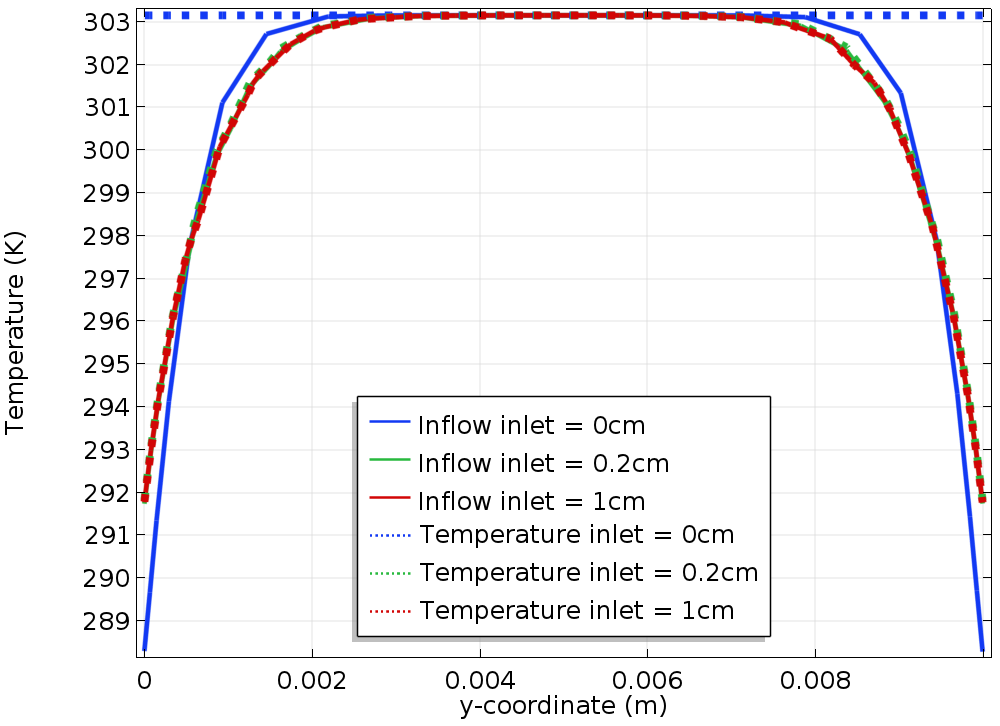
我们来看一下 U_in=10cm/s 的结果。在下图的左侧，我们可以看到使用温度 边界条件（顶部）和流入 边界条件（底部）的温度分布。这两张图看起来非常相似，很难从中得出任何结论，但右边的图提供了更多细节。

右图显示了沿位于冷却区开始处的垂直线的温度曲线。（当 L_inlet=0 时，它与入口边界重合。在本文的其余部分，我们称其为“参考线”。）实线表示使用 流入 边界条件获得的结果，虚线对应于温度 边界条件。不同的颜色对应于不同的 L_inlet 值。

首先检查使用温度 边界条件（虚线）获得的结果。我们看到，随着 L_inlet 的增加，沿参考线的温度曲线收敛于给定的曲线。 L_inlet=2cm 处的结果显示没有改善；它们与 L_inlet= 1cm 处获得的结果一致，因此我们可以认为不需要进一步扩展通道。

对于 L_inlet=0，温度曲线与收敛曲线完全不同。这说明使用温度 边界条件出现了典型问题：由于沿参考线的温度分布事先不知道，因此最好的选择是规定一个合理的温度；这里是上游温度。

当使用流入边界条件时，随着 L_inlet 的值增加，沿参考线的温度曲线会收敛到与使用温度边界条件时相同的收敛曲线。

我们注意到，尤其当 L_inlet= 0 时，解比使用温度边界条件时更接近收敛曲线。

左:通道中的温度场，使用温度边界条件(顶部)和流入边界条件(底部) L _inlet=0 和 U_in=10cm/s。右:沿基准线的温度与流入边界条件(实线)和温度边界条件(虚线)。

重要的是要记住，在许多项目中，几何体包含由几何体中未表示的通道供给的入口。虽然对于简单的几何形状，就像这里，很容易修改它以在入口之前包括一部分通道，但对于高级几何形状可能具有挑战性。即使 L_inlet=0，流入边界条件也能很好地预测入口处的温度分布。

当入口前的通道可以延伸足够的距离时，使用流入 和温度 边界条件获得的入口边界上的温度分布是一致的。这与之前的分析一致，当对流换热占主导地位并使用理想气体模型时，流入 边界条件与温度边 界条件相似。这里有趣的是，从数值的角度来看，这两种情况在这种情况下表现相似。（例如，非线性求解器采用的迭代次数在两种情况下都是相同的。）

除了温度分布之外，另一个应该监测的量是由热通量引起的热率。下表中包含了不同 L_inlet 值的热耗率。一列包含流入 边界条件的值，另一列包含温度 边界条件的值。

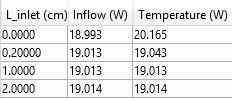
表中列出了最高入口速度情况下的热耗率。

当使用流入 边界条件时，加热速率几乎是恒定的。使用时温度 边界条件时，热耗率受 L_inlet 影响。

最低入口速度的模拟结果

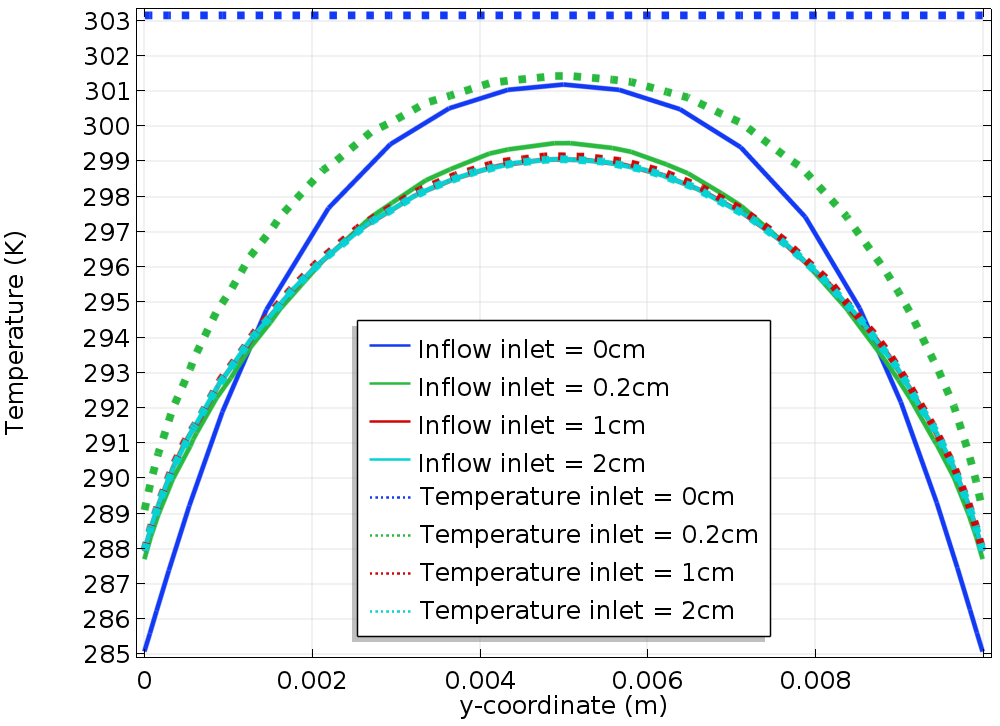
因为在这种情况下速度较低，对流的影响不再占主导地位。下图左侧显示了使用温度 边界条件(顶部)和流入 边界条件(底部) 获得的温度场。虽然这两个图看起来很相似，但仔细观察就会发现，在入口边界的末端，两个温度曲线图之间存在差异。

右边的图显示了沿参考线的温度曲线。如前所述，实线表示使用流入 边界条件获得的结果，虚线对应温度 边界条件获得的结果，不同的颜色对应不同的 L_inlet 值。

同样，对于 L_inlet=0，温度 边界条件规定了沿参考线的恒定温度。该温度曲线与 L_inlet 的最大值所获得的解相差甚远。和以前一样，我们看到随着 L_inlet 增加，温度收敛到给定的曲线。然而，与 U_in=10cm/s 的情况相比，这里的收敛速度较慢。比较使用流入 边界条件和温度 边界条件获得的解，我们注意到对于任何 L_inlet 值，使用流入 边界条件总是更接近收敛曲线。

左: 对于 L_inlet=0 和 U_in=1cm/s，使用温度边界条件(顶部)和流入的边界条件(底部)获得的通道中的温度场。右:沿流入边界条件(实线)和 温度边界条件(虚线) 参考线的温度比较。

下表再次显示了两种边界条件下的加热耗率。

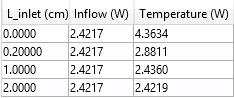
表中列出了最低入口速度情况下的热耗率。

趋势与第一种情况类似，但当使用温度 边界条件时，L_inlet 对热耗的影响要大得多。使用 L_in=0 的温度 边界条件，与使用长入口获得的解相比，热耗率值被高估了近 2 倍。使用流入 边界条件，可以正确预测任何 L_inlet 值的热耗率。

这些结果表明，当 L_inlet 很小(尤其是当 L_inlet=0)，使用流入 边界 条件而不是均匀的温度 边界条件获得的温度分布和热通量更真实。这可以用这样一个事实来解释，即在入口处，均匀的温度分布是不现实的。在实际情况下，温度不是在入口处精确控制的，而是在例如位于一定距离的储罐中控制的。

总结性思考

虽然在许多配置中，温度和流入特征描述了类似的条件并导致类似的模拟结果，但有许多配置（特别是对于流速满和小尺寸），其中热传导的影响相对于对流换热不可忽略，并且使用流入 边界条件通常会导致温度曲线比使用温度边界条件更接近现实。此外，温度边界条件可能会强制使用错误的温度值，从而导致不现实的大热通量。

流入边界条件使用简单，通常不会导致额外的需要求解的数值成本，它应该是确定流动入口处传热条件的首选。COMSOL 案例库中的绝大多数模型示例都使用它。

下一步

单击下面的按钮，了解更多关于 COMSOL Multiphysics 中传热建模的所有可用功能。

符号

C_p：热容（SI 单位：J/K/kg）

h：传热系数（SI 单位：W/m²/K）

\mathbf{n}: 边界法向量（SI单位：1）

k: 导热系数 (W/K/m)

p：压力（SI单位：Pa）

\mathbf{q}: 热通量 (SI 单位: W/m²)

p_{\mathrm{upstream}}：上游压力（SI单位：Pa）

T：温度（SI单位：K）

T_{\mathrm{cold}}, T_{\mathrm{hot}}: 冷热温度（SI 单位：K）

T_{\mathrm{upstream}}：上游温度（SI单位：K）

U_{\mathrm{in}}：入口速度（SI 单位：m/s）

\alpha_p：热膨胀系数（SI 单位：1/K）

\rho: 密度 (SI 单位: kg/m³)

\mathbf{u}：速度（SI 单位：m/s）

\Delta H: 焓变 vs. 参考焓 (SI 单位: J/kg)