
在进行结构力学分析时,我们不可避免地会遇到几何非线性的概念。在这博客文章中,我们讨论了几何非线性的含义以及什么时候应该考虑几何非线性带来的影响。
引言
在有关结构力学的基础课程中,几何非线性的概念甚至可能不会明确引入。实际上,在结构力学分析中,通常默认为几何线性。在几何线性设置中,平衡方程是在未变形状态下建立的,并且不会随变形而更新。这听起来似乎有些令人惊讶,因为计算变形是结构力学的全部目的。
但是,在大多数工程问题中,变形是非常小的,以至于与原始几何形状的偏差是不可察觉的。通过忽略变形而引入的小误差并不能保证由更复杂的理论所产生的额外的数学复杂性。这就是为什么绝大多数分析都是在假设几何线性的情况下进行的。
在许多情况下,我们无法忽略变形,并且并不是所有这些情况都包含我们直观上认为的较大的变形。
考虑几何非线性的影响
在 COMSOL Multiphysics 建模过程中考虑几何非线性时,对数学的最重要影响是:
- 在 空间 框架和 材料 框架之间进行了区分。由于存在位移矢量(\mathbf u),某一点的空间坐标(\mathbf x)与材料坐标(\mathbf X)不同,即 \mathbf x = \mathbf X + \mathbf u。因此,在表达式中使用大写或小写坐标名称将非常重要。
- 应变由格林-拉格朗日应变张量代替工程应变来表示。
- 应力由第二类 Piola-Kirchoff 应力张量表示。
- 压力载荷考虑了变形。边界的法线将更新,并且考虑拉伸引起的面积变化。
在之前的博客文章中,我们了解了有关不同应力和应变张量的一些信息,但是这里需要对应变度量进行一些详细的论述。为此,我们通过考虑应变张量的某些分量来研究线性应变与完全非线性应变之间的差异。
X– 方向的格林-拉格朗日法向应变可写为
如果省略了二次项,就回到了我们熟悉的工程应变方程:
对于剪切应变,格林-拉格朗日应变分量为
同样,通过忽略非线性项来获得工程应变:
明显(或不太明显)的旋转
当结构发生明显旋转时,基础理论中使用的工程应变将不再提供有用的表示。刚体的旋转会导致工程应变张量的非零分量,这将通过本构定律引起应力,但是由于物理原因,应力不该出现在刚体中。另一种看法是,任何有用的应变张量都必须能够反映出在刚体运动中不存在拉伸或相对角度变化的事实。
考虑一个绕原点在 xy 平面上刚性旋转的二维物体。下图显示了一个简单的线性平面应力模型,其中矩形钢板旋转了 10°。
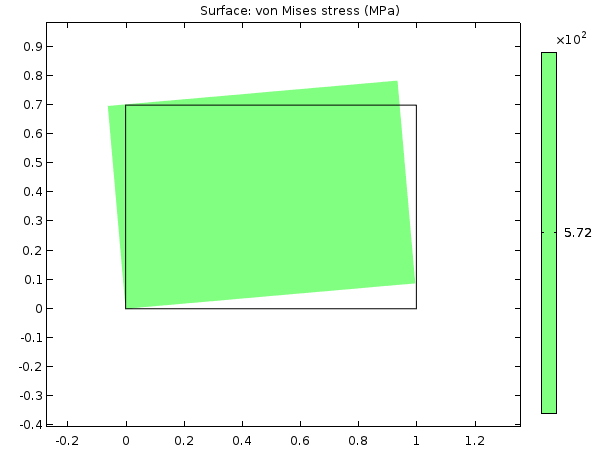
无几何非线性旋转 10° 的矩形钢板的等效应力
结果是等效应力为 572MPa,高于大多数最常见钢材的屈服极限。要了解为什么会发生这种情况,我们需要研究解析解:
原先位于(X,Y)的点将移至新的位置(x,y),由下式表示
x = X \cos(\phi)-Y \sin(\phi) \\
y = X \sin(\phi) + Y \cos(\phi)
\end{matrix}
这意味着位移(u,v)为
u = x-X = X (\cos(\phi)-1)-Y \sin(\phi) \\
v = y-Y = X \sin(\phi) + Y (\cos(\phi)-1)
\end{matrix}
工程应变将变为
\epsilon_X = \frac{\partial u}{\partial X} = \cos(\phi)-1 \\
\epsilon_Y = \frac{\partial v}{\partial Y} = \cos(\phi)-1 \\
\epsilon_{XY} = \frac{1}{2}(\frac{\partial u}{\partial Y}+\frac{\partial v}{\partial X}) = -\sin(\phi)+ \sin(\phi) = 0
\end{array}
对于刚体旋转,所有应变应为零,但显然其中两个应变分量不是零。金属通常会在 0.001 量级的应变下屈服。这种大小的虚拟应变在 2.5° 旋转时已经发生。为了使应变小于 0.0001,刚性旋转不得大于 0.8°。这意味着,即使是在我们经常希望的“小角度近似”充分的角度下,也必须使用几何非线性方法。
使用与上述相同的刚体旋转,但使用格林-拉格朗日应变,得出
现在,对于任何旋转值,该应变张量分量均为零。对于所有格林-拉格朗日应变张量以及任意旋转,都可以显示此性质。
通过使用几何非线性公式,可以避免出现此类应力伪影。通过求解考虑几何非线性的同一个问题,可以证实这一点。现在,应力水平是纯数字噪声;比屈服极限低 12 个数量级。
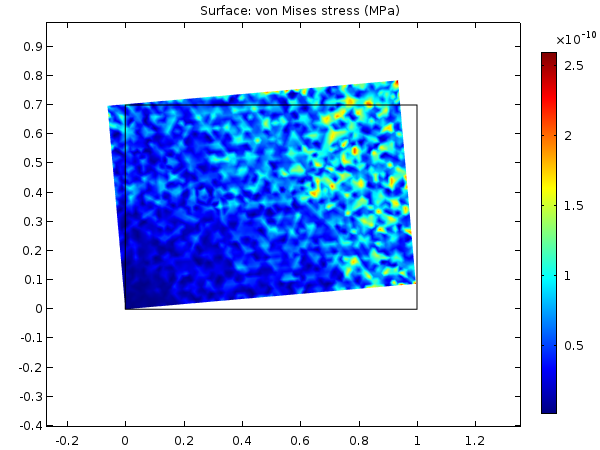
使用几何非线性时,在 10° 旋转时的等效应力。
薄结构拉伸
以下面草图中的两个梁为例:

具有不同端部约束条件的梁。
在右端,上面的梁可以自由地水平移动,而下面的梁则不能。在线性理论中,如果梁承受垂直载荷,那么这两个端部条件是等效的。轴向作用和弯曲作用之间没有耦合。但是,在几何非线性分析中,不同的端部条件将导致完全不同的结果:
- 当末端自由轴向移动时,梁的垂直位移几乎与几何线性情况相同。
- 当限制轴向位移时,垂直位移将小于线性情况,并且对载荷具有很强的非线性依赖性。
当梁偏转时,如果末端不能向内移动,那么它的中心线就会被拉伸。这将引入很大的轴向力,从而使梁在拉力方面的作用类似于张力中的钢丝——拉力越高,它抵抗横向力的能力就越大。
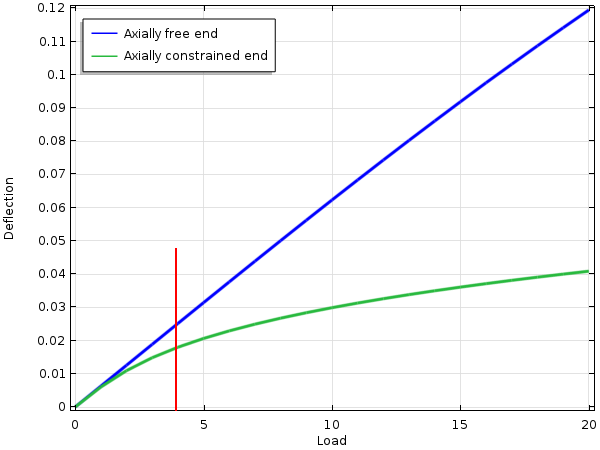
正方形横截面为 0.05 x 0.05 的梁的中点挠度。红线表示线性分析中的挠度为 0.025 (梁高度的一半)时的载荷。
同样的想法也适用于板和壳。如果边界条件使挠度引起平面内张力,那么随着挠度的增加,板将会变得更加坚硬。
有一条经验法则规定,如果线性分析中的梁或板的挠度超过其厚度的一半,那么就应考虑几何非线性效应。上图中的红线就表明了这一点。
应力刚化
如前面的示例所示,结构的刚度有时会由于几何非线性效应而发生显著变化。有时我们将它称为 应力刚化。这个术语有些误导,因为刚度也有可能降低。如果我们向上方梁施加压缩轴向载荷,那么其横向刚度实际上会降低。
例如,在旋转系统中,离心力可能会引入明显的拉应力。因此,应力刚化很重要。这会导致系统的本征频率随转速的增加而增加。
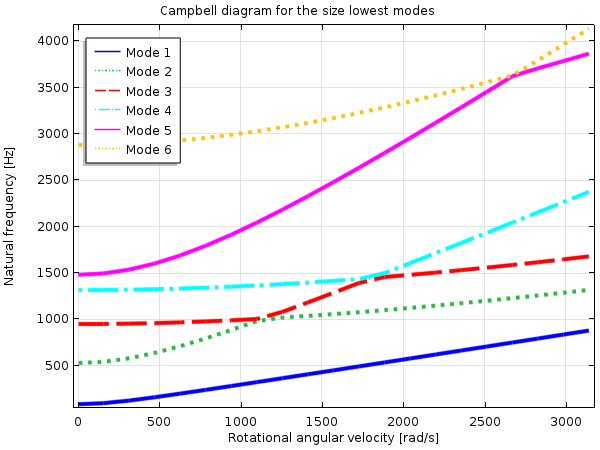
坎贝尔图显示了旋转叶片的固有频率如何随旋转速度变化。
通常,导致预应力的载荷与我们实际执行分析的载荷不同。因此,可能有两个不同的载荷系统必须分别进行分析。
在 COMSOL Multiphysics 中,有两种预定义的研究类型专门用于分析预应力系统:
- 预应力分析,特征频率
- 预应力分析,频域
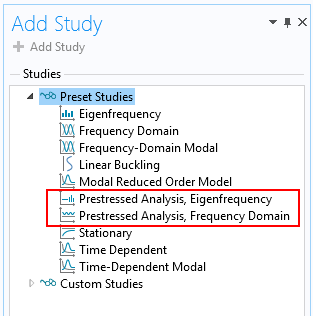
用于分析预应力结构的研究类型。
这些研究类型包括两个研究步骤,其中第一步用于计算预应力状态。此研究可以是线性的也可以是非线性的。第二个研究步骤本身是线性的,但是在建立刚度矩阵时包括了由几何非线性引起的非线性项。
如果您对应力刚化的重要示例感兴趣,请查看以下模型案例:
屈曲
屈曲 或载荷达到某个临界值时的失稳是由几何非线性效应引起的。在COMSOL Multiphysics中,有一种特殊的研究类型称为线性屈曲,用于计算临界载荷的一阶近似值。
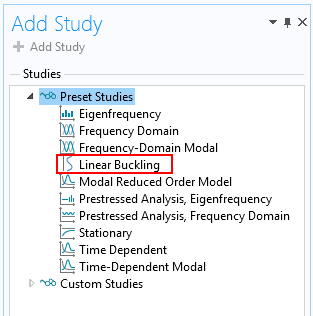
线性屈曲研究类型。
在线性屈曲研究中,通过求解特征值问题可以获得近似屈曲载荷。
作为替代方案,我们可以跟踪完整的非线性响应,直到临界点,甚至超过临界点。在这种情况下,我们必须以较小的步长增加载荷。这种方法的计算量明显增加,但更准确。
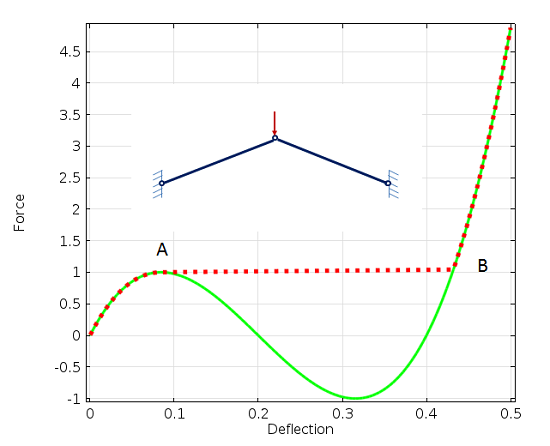
在 A 点屈曲塌陷的载荷-挠曲历史
您可以在上一篇博客文章中了解有关屈曲的更多信息。
在 COMSOL Multiphysics 中启用几何非线性
启用几何非线性
几何非线性是研究步骤的属性。对于与之相关的那些研究类型,该研究设置中有一个复选框。
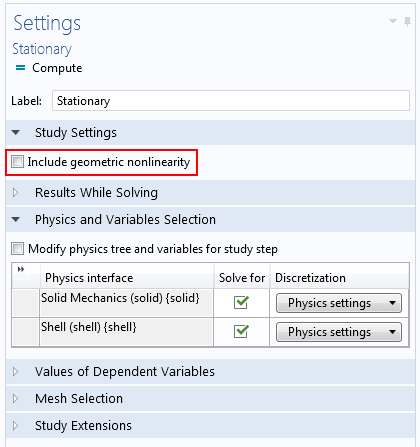
静态研究的设置。
有时,这个复选框是预先选中的,我们无法更改。当我们在模型树中包含某些不能在线性情景中使用的物理节点时,就会发生这种情况,例如:
- 超弹性材料
- 大应变塑性
- 接触
请注意,大多数非线性材料模型(例如非线性弹性或蠕变)并不假定几何非线性。
求解几何非线性问题
几何非线性问题通常是高度非线性的,因此在为求解器提供设置时需要考虑到这一点。
以上述提到的固定端的梁为例。当求解非线性问题时,第一次迭代后的解将与线性问题的解相同,从而使梁上的所有点在横向载荷下仅垂直移动。
因此,在第一次迭代之后,梁将出现明显的轴向伸长。这种伸长与轴向力有关。由于没有净轴向力(该方向没有外部负载),因此该力最终将作为下一次迭代的残余力。这个不平衡力可能大于施加的负载。对于非线性求解器,这似乎是一个非常棘手的问题,求解器通常会引入阻尼。
幸运的是,这些问题通常表现得比数字指示的要好。我们可以通过使用比默认方法更为激进的迭代方案来明显加快求解的速度。
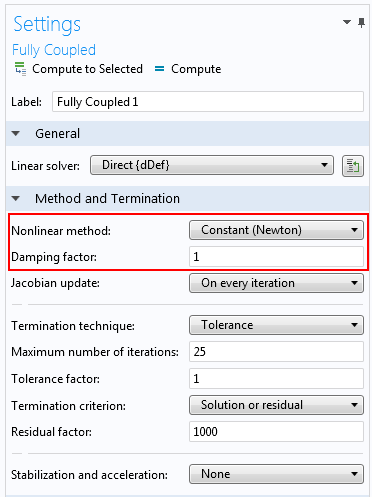
全耦合求解器的设置。
使用恒定牛顿而不是自动自适应方案将导致求解器进行较大的更新。阻尼系数可以设置为1(无阻尼),也可以设置为 0.9。
在大多数情况下,几何非线性是非线性的唯一来源,并将对特定载荷水平具有唯一的解。从这个意义上讲,我们可以使用仅具有单个载荷的静态分析来分析问题。出于收敛的原因,有时最好使用参数连续求解器逐渐增加载荷。
COMSOL 案例库中的夹紧的半球壳教程模型中显示了如何设置求解器来解决严重非线性问题的示例。
结束语
如上所述,在求解结构力学问题时,有几种情况必须考虑几何非线性。那么,为了安全起见,为什么我们不总是在模型中加入这种影响呢?
- 即使非线性影响很小,调用非线性求解器也会带来更长的求解时间。对于小型模型而言,这不是问题,但是当使用数百万个自由度进行求解时,将求解时间减少两倍确实很重要。
- 有时我们希望能够与解析解进行比较,而此类解通常基于线性理论。
- 我们可能需要遵循假定使用线性方法的标准或分析过程。
- 在几何非线性问题中,必须使用实际载荷。如果我们只想对结构响应进行概念研究,那么如果估算的载荷太大,则解可能不会收敛。






评论 (9)
贵 王
2024-12-04你好,我在用comsol求解激光熔覆薄板过程中热力耦合问题用到动网格,然后就不能使用结合非线性了,选择几何非线性就无法求解,请问这种问题怎么解决
Yuqing Ge
2024-12-06 COMSOL 员工结构力学本身就是计算变形,不需要也不能和动网格搭配使用。您的问题涉及具体的模型设置细节,建议发送到技术支持中心,由工程师帮您查看:https://cn.comsol.com/support
匡骑 李
2025-03-11您好,我在对两端固定的梁中间施加载荷并逐步增大载荷的过程中进行线性屈曲分析,绘图为载荷大小与中间位移的关系,参数化扫描后绘图的结果和单一的载荷下的位移结果不一致是为什么?且参数化扫描载荷的情况下中间的位移很小,与我所阅读的论文结果不匹配
Kaixi Tang
2025-03-19 COMSOL 员工您好,您的问题可能和模型具体设置有关,您可以先参考线性屈曲官方案例:https://cn.comsol.com/model/buckling-analysis-of-a-truss-tower-12579,如果仍不能解决,您可以将模型发送到技术支持查看:cn.comsol.com/support。
Wenyang Liu
2025-06-09您好,我在用comsol做大变形仿真时自定义变形梯度等物理量,这里面用到的坐标系用小写字母(空间坐标系)时可以识别变量,但改用大写字母(材料坐标系)时无法识别,这篇文档里有强调坐标名称大小写的重要性,如何解决上述问题呢,谢谢!
Yuqing Ge
2025-06-17 COMSOL 员工COMSOL中的材料和空间坐标系变量在任何地方都可以直接使用的,您遇到的问题应该与您定义的具体变量有关,您可以将问题发送到技术支持中心:https://cn.comsol.com/support
宇蒙 孙
2025-07-04您好,计算单向耦合计算热膨胀时候需要考虑几何非线性吗
Zhengyu Shi
2025-12-23请问下,机械结构,大位移下的谐振频率随位移的变化如何仿真?
Esther Du
2025-12-29 COMSOL 员工您好,您可将您的具体问题描述以及模型发至技术支持中心https://cn.comsol.com/support, 以便于我们具体讨论分析。这里先向您推荐相关案例《预应力频率响应分析》https://cn.comsol.com/model/bracket-structural-mechanics-tutorials-10314。研究类型包括两个研究步骤,其中第一步用于计算预应力状态,此研究步骤可以是线性的也可以是非线性的;第二个研究步骤本身是线性的,但是在建立刚度矩阵时包括了由几何非线性引起的非线性项。