我们生活在一个三维世界——或许是四维，如果考虑到时空的话。然而，在工程分析中通过二维近似来节省模拟时间和计算资源的情况很常见。在这篇博客中，我们将介绍什么时候，以及如何使用二维公式研究固体力学领域中的问题。
目录
编者按：这篇博客更新于 2022 年 12 月 16 日，以显示 COMSOL Multiphysics® 软件 6.1 版本中的新特征和新功能。
什么是二维？
在现实生活中，没有多少东西是二维的。例如，当我们在二维中研究电缆横截面周围的电磁场时，我们实际上是在说:“这条电缆又直又长。距离两端足够远时，电场只取决于横截面上的位置。”对于大多数物理问题，思路是这样的:在二维近似中，我们研究一个长而直的物体的横截面，忽略端点效应。
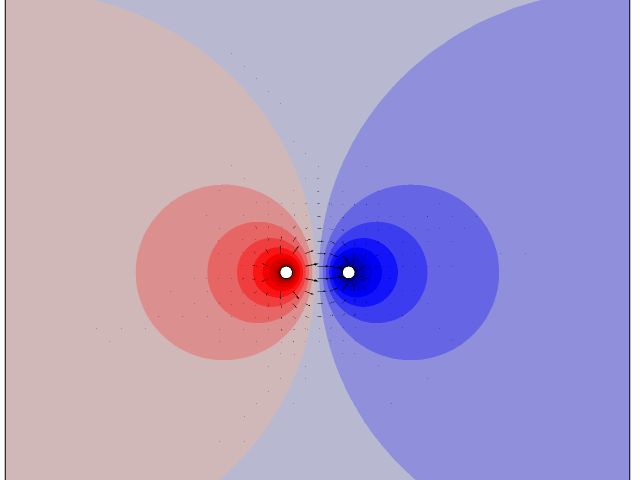
在二维中计算的两根具有不同电势的长电缆周围的电势 (用颜色表示)和电场(用箭头表示)。
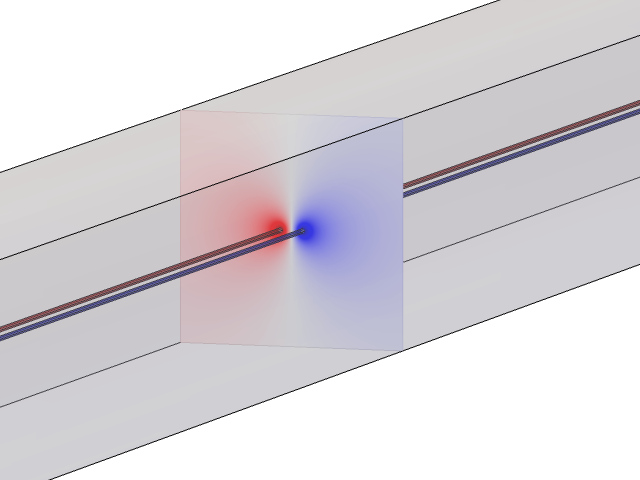
又长又直且互相平行的电缆横截面
为什么固体力学很特别?
在固体力学领域，二维状态比较长的拉伸有更多的可能性。例如，我们可以将一个仅在其平面上承受载荷的薄平板看作二维。那么，固体力学有什么特别之处使这成为可能呢?
考虑对上述平板进行传热分析。在这种情况下，大表面将在面外方向产生对流和辐射。其次，厚度方向的温度梯度很重要。因此，通过二维近似薄平板中的热量传递比较困难。类似的推理也可以应用于许多其他物理现象。
固体力学领域也存在面外方向的影响。薄平板通常在横向上产生变形。例如，如果拉伸平板，它就会变薄。然而，这并不会直接影响此二维问题的解。如果你感兴趣的话，可以通过后验计算厚度变化的结果，这将在下文进行更详细的讨论。
固体力学中的二维公式
在接下来的部分，假定 xy 平面表示二维平面，z 为面外方向。xy 平面上的位移分别称为 u 和 v，w 为 z 方向上的位移。
需要注意的是，如果面内作用和面外作用之间没有耦合(例如，当线弹性材料的泊松比为零时)，所有公式将是相同的。
平面应变
平面应变是二维固体力学公式中唯一不包含近似值的公式。在两个刚性壁之间的 z 方向上受到约束的物体中将存在平面应变状态。这也是在概念上与其他物理领域中的二维公式具有最佳对应的公式。然而，该物体并不一定要在 z 方向上是“长”的。这是与大多数其他物理领域中的二维近似的根本区别。
该假定的表示简单:在 z 方向没有位移。
{\begin{array}{*{10}{l}}
u&=&u \left ( x,y \right ) \\
v&=&v \left ( x,y \right ) \\
w&=&0
\end{array}}
{\ }
\]
这同样可以用应变来表示:
{\begin{array}{*{10}{l}}
u&=&u \left ( x,y \right ) \\
v&=&v \left ( x,y \right ) \\
\varepsilon_{zz}&=&\varepsilon_{xz}&=&\varepsilon_{yz} &=& 0
\end{array}}
{\ }\]
请注意，为了完全避免端部效应，实际上假定刚性壁面的边界条件是辊支撑类型，因此在 xy 平面上的位移不受抑制。如果不是这样，就又回到了我们研究远离终点的长物体的情况。
平面应力
在平面应力公式中，假定与 z 方向有关的三个应力张量分量为零。这是薄板的一个很好的近似，但只有在厚度趋近于零的极限情况下才完全正确。
v&=&v \left ( x,y \right ) \\\sigma_{z}&=& \sigma_{xz}&=&\sigma_{yz}&=& 0\end{array}}{\ }
在自由表面上，平面应力的局部状态始终存在，因为这正是边界条件。这就是平面应力假设如此有效的原因——它在板的两侧都是完全正确的，并且只要厚度很小，内部就不会产生显著的 z 方向应力。
广义平面应变
然而，广义平面应变没有唯一的定义，这通常意味着普通平面应变公式的一些假定是放宽的。假定整个应变张量非零，但仍然只取决于 x 和 y，则可以用下列位移场表示这种应变张量:
{\begin{array}{*{10}{l}}
u&=&u \left ( x,y \right ) – \frac{a}{2} z^2 \\
v&=&v \left ( x,y \right ) – \frac{b}{2} z^2 \\
w&=&\left (ax + by +c \right )z
\end{array}}
{\ }
\]
式中，a，b,c 是常数。无限小的面外应变将表示为
在执行分析的 z=0 平面，w 为零。因此，位移场仍然只有两个分量，u 和 v 需要求解。然而，存在三个新的未知数，a，b 和 c。在广义平面应变的一般解释中，只使用系数 c。实际上，这意味着长物体可以在 z 轴方向上膨胀。如果系数 a 和 b 也包括在内，也允许拉伸以一个恒定的曲率弯曲。a，b，c 的值取决于横截面上无净轴力和弯矩的假定；也就是说，终端是自由的。
当您在 COMSOL Multiphysics 中选择广义平面应变选项时，可以在纯纵向拉伸假定和启用面外弯曲之间进行选择。
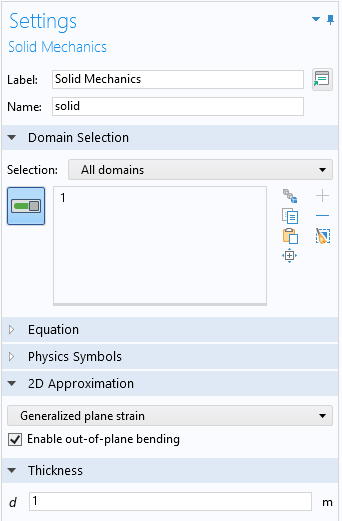
选择广义平面应变。
还有其他的公式有时被称为广义平面应变。例如面外剪切应变，可被允许 \varepsilon_{xz} 和 \varepsilon_{yz} 为非零。这种公式与 \varepsilon_{zz} = 0，一起被用于弹性波，时域显式 接口的二维版本。
本构模型
在线弹性假定下，胡克定律可专用于平面应变和平面应力。胡克定律的完整三维形式如下：
{\begin{array}{*{10}{l}}
\sigma_x &=& \frac{E}{1+\nu} \left( \varepsilon_{xx} +\frac{\nu}{1-2 \nu} \left ( \varepsilon_{xx} + \varepsilon_{yy} + \varepsilon_{zz} \right )\right ) \\
\sigma_y &=&\frac{E}{1+\nu} \left( \varepsilon_{yy} +\frac{\nu}{1-2 \nu} \left ( \varepsilon_{xx} + \varepsilon_{yy} + \varepsilon_{zz} \right )\right ) \\
\sigma_z &=&\frac{E}{1+\nu} \left ( \varepsilon_{zz} +\frac{\nu}{1-2 \nu} \left ( \varepsilon_{xx} + \varepsilon_{yy} + \varepsilon_{zz} \right )\right ) \\
\tau_{xy} &=& 2G \varepsilon_{xy} \\
\tau_{yz} &=& 2G \varepsilon_{yz} \\
\tau_{xz} &=& 2G \varepsilon_{xz} \\
\end{array}}
{\ }
\]
式中，E 为杨氏模量，ν 为泊松比，G 为剪切模量。
平面应变
平面应变的情况比较简单，只需要从三维公式中删除三个为零的应变分量
{\begin{array}{*{10}{l}}
\sigma_x &=& \frac{E}{1+\nu} \left( \varepsilon_{xx} +\frac{\nu}{1-2 \nu} \left ( \varepsilon_{xx} + \varepsilon_{yy} \right )\right ) \\
\sigma_y &=&\frac{E}{1+\nu} \left( \varepsilon_{yy} +\frac{\nu}{1-2 \nu} \left ( \varepsilon_{xx} + \varepsilon_{yy} \right )\right) \\
\sigma_z &=&\frac{E \nu}{(1+\nu)(1-2 \nu)} \left( \varepsilon_{xx} + \varepsilon_{yy}\right ) &=& \nu \left ( \sigma_x + \sigma_y \right )\\
\tau_{xy} &=& 2G \varepsilon_{xy} \\
\tau_{yz} &=& 0 \\
\tau_{xz} &=& 0 \\
\end{array}}
{\ }
\]
平面应力
对于平面应力，可以使用 \sigma_z = 0 来消除 \varepsilon_{zz}，从而得到
{\begin{array}{*{10}{l}}
\sigma_x &=& \frac{E}{1-\nu^2} \left( \varepsilon_{xx} +\nu \varepsilon_{yy} \right) \\
\sigma_y &=& \frac{E}{1-\nu^2} \left( \varepsilon_{yy}+\nu \varepsilon_{xx} \right) \\
\sigma_z &=& 0 \\
\tau_{xy} &=& 2G \varepsilon_{xy} \\
\tau_{yz} &=& 0 \\
\tau_{xz} &=& 0 \\
\end{array}}
{\ }
\]
横向应变(即厚度变化)可由解计算为：\varepsilon_{zz} = – \frac {\nu} {1-\nu} (\varepsilon_{xx} + \varepsilon_{yy})。
然而，COMSOL Multiphysics® 软件中不使用这个公式，而是使用完整的三维胡克定律与额外的未知场共同表示\varepsilon_{zz}。当然，这增加了问题的总体规模，但优势显著:不需要考虑所有材料模型的特殊平面应力形式，不需要修改例如热膨胀以及类似的特性。如果绘制横向应力，你会注意到这个值并不等于零，因为它是用胡克定律从应变场计算出来的。
广义平面应变
这个案例有点复杂。当在本构关系中引入面外应变的假设时，应力分量通过系数 a、b 和 c 显式取决于坐标 x 和 y。
{\begin{array}{*{10}{l}}
\sigma_x &=& \frac{E}{1+\nu} \left( \varepsilon_{xx} +\frac{\nu}{1-2 \nu} \left ( \varepsilon_{xx} + \varepsilon_{yy} + ax +by +c \right )\right) \\
\sigma_y &=&\frac{E}{1+\nu} \left( \varepsilon_{yy} +\frac{\nu}{1-2 \nu} \left ( \varepsilon_{xx} + \varepsilon_{yy} + ax +by +c \right )\right) \\
\sigma_z &=&\frac{E}{1+\nu} \left( ax +by +c +\frac{\nu}{1-2 \nu} \left ( \varepsilon_{xx} + \varepsilon_{yy} + ax +by +c \right )\right) \\
\tau_{xy} &=& 2G \varepsilon_{xy} \\
\tau_{yz} &=& 0 \\
\tau_{xz} &=& 0 \\
\end{array}}
{\ }
\]
不可压缩材料
可压缩程度越小，面内和面外作用之间的耦合越强。尤其是许多关于塑性、蠕变和超弹性的模型都假定不可压缩性。当使用这种材料模型时，所选择的二维假设的影响尤为显著。
我应该选择哪种公式?
我们来看一个简单的例子，中心有一个圆孔的矩形板。我们从一块非常薄的板开始，逐渐移动至一个厚物体，其中的圆孔看起来更像是一条长长的隧道。
平面内板的尺寸为 2 m x 1 m，孔直径为 0.4 m。施加 1 MPa 的拉伸载荷。使用钢的材料数据。平面应力的解如下图所示。
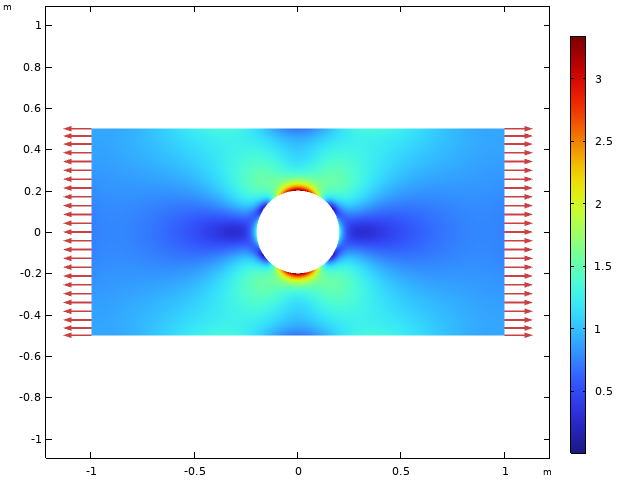
在平面应力假设下，求解的Von Mises 等效应力。
在平面应力假设下，横向应力 \sigma_{z} 为零。
接下来，我们来看一个完整的三维解，并再次观察相同的对象，但厚度分别为 0.1、1 和 10 m。下图中绘制了横向应力 \sigma_{z}。
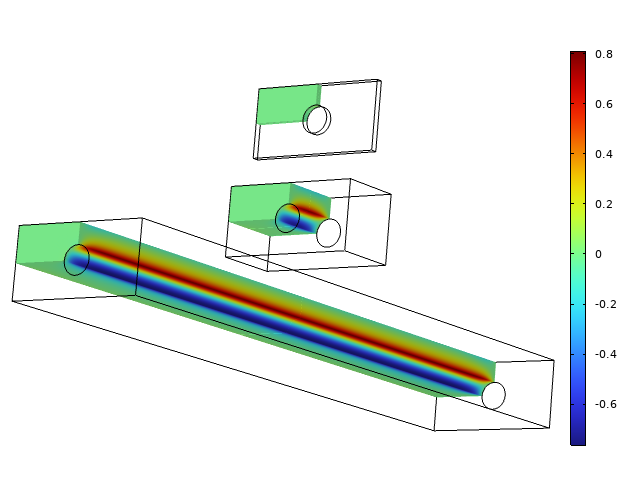
三种不同厚度的横向应力。
对于薄结构，横向应力可以忽略不计，因此平面应力是一个很好的假设。对于中间厚度的板，应力为完整的三维状态。对于较长的物体，除了两端位置外，横向应力是恒定的。请注意，最大横向应力为 0.8 MPa，因此与施加荷载相比，不可忽略。
接下来，我们对孔顶部应力最大处的横向应力进行更详细的研究。
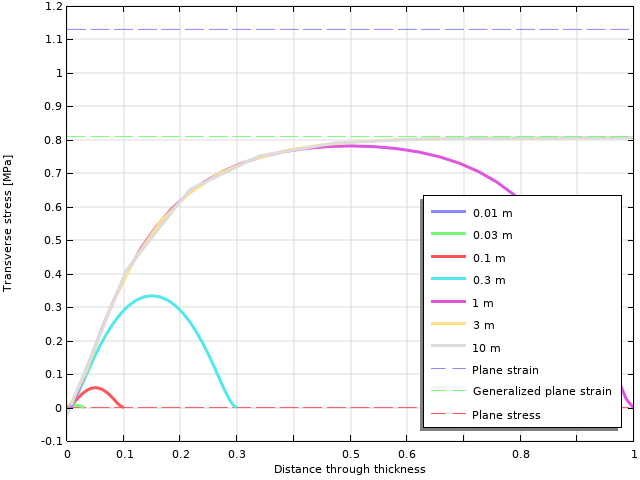
沿厚度方向分布的横向应力变化。图中参数为物体的厚度。
可以看出，只要厚度大于等于 1 m，即可达到约 0.8 MPa 的峰值水平。厚度越小，最大横向应力下降越快。
这幅图将帮助我们澄清两个常见的误解:
- 仅因为一个物体在横向上是自由的，并不能说明它处于平面应力状态。
- 长物体不一定处于平面应变状态，这只有在两端固定的情况下才成立。
事实是:
- 具有自由边界的薄物体可以用平面应力近似。
- 远离端点的具有自由边界的长物体，可以通过广义平面应变近似。
- 具有与面内尺寸相当厚度的物体必须被看作全三维。
在实践中，“厚的物体应当被认为是处于平面应变状态”这一说法在教科书和网上几乎随处可见。虽然在这种情况下，平面应变确实比平面应力更好近似，但它仍然是不准确的。此时假设为广义平面应变更为准确。
我个人的猜测是，由于使用二维解可以追溯到许多问题都是用笔和纸解决的年代，例如，使用艾里应力函数，所以在实践中需要在平面应力和平面应变之间进行选择。使用有限元软件，对于较厚的物体，全三维或广义平面应变是更好的选择。
为什么会发生横向应力？
在上述示例中，我们已经看到横向上产生了显著的应力，即使物体在那个方向自由移动。为什么会出现这种情况?这是由于泊松比效应，使得面外方向有厚度变化。只要在平面内存在应力(和应变)梯度，这种厚度变化就不是均匀的。在应力集中的位置，如板上的孔，应力最大的点处的材料希望比周围的材料更薄，而相邻的材料则与之相反，并试图抑制变形。
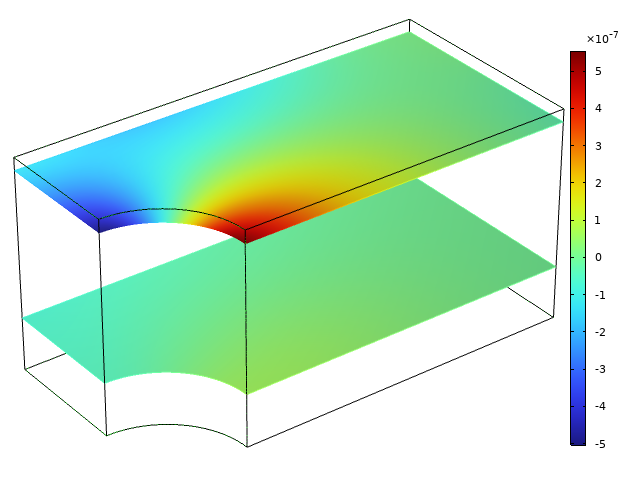
远离自由表面(底部)和靠近自由表面(顶部)的横向位移变化。在每个平面上，平均位移被设为零。
在上一节中，我们注意到横向应力的大小随与自由边界的距离变化。详细的应力分布也随距自由表面的距离而变化，如下图所示。
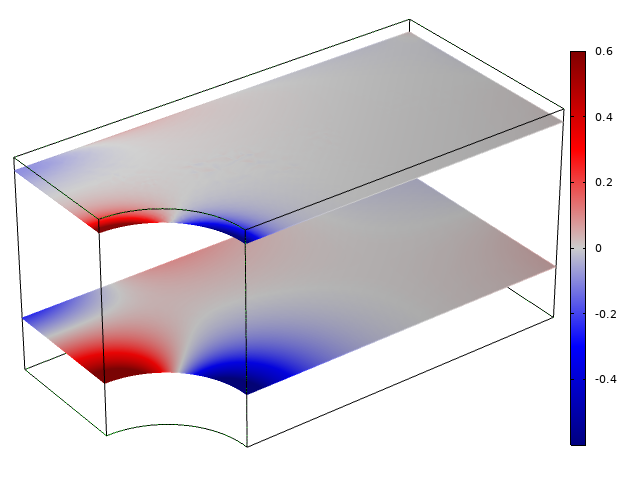
远离自由表面(底部)和靠近自由表面(顶部)的横向应力分布。将两个切面上的应力场按比例调整为峰值相同;接近边界处的实际应力较低。
在远离自由表面的地方，横向应力与面内应变成正比 \varepsilon_x+\varepsilon_y。由于周围材料的约束作用，整个剖面的厚度基本保持均匀。在接近自由表面的地方，当面内应变梯度较大时，横向应力反而较高；在这个案例中，此位置是靠近孔的边缘。
面内应力会怎么变化？
只要结构仅受牵引力(而不是规定的位移)载荷，那么平面内的应力状态即可脱离二维假设，至少对于线弹性来说是这样的。然而，这并不是全部的清凉。在下图中，x 方向的应力显示孔的顶部是应力最集中的位置。
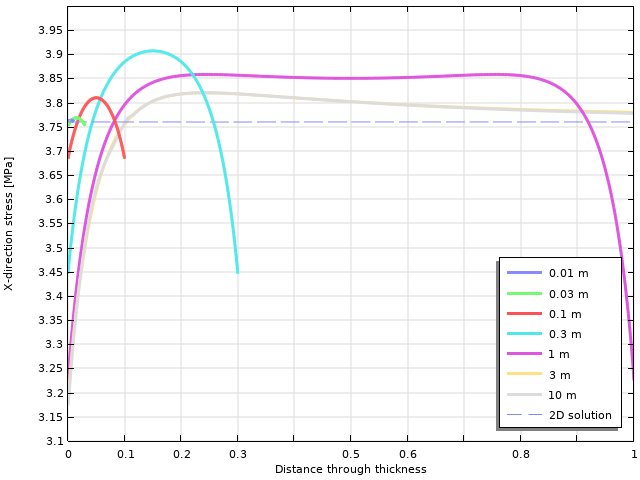
整个厚度方向上的水平应力变化。图中的参数为物体的厚度。
可以看出，厚度存在显著的变化。对于薄的物体，二维结果很准确，而对于厚的物体，结果存在很大的差异，特别是在自由表面。这对等效应力也有影响。
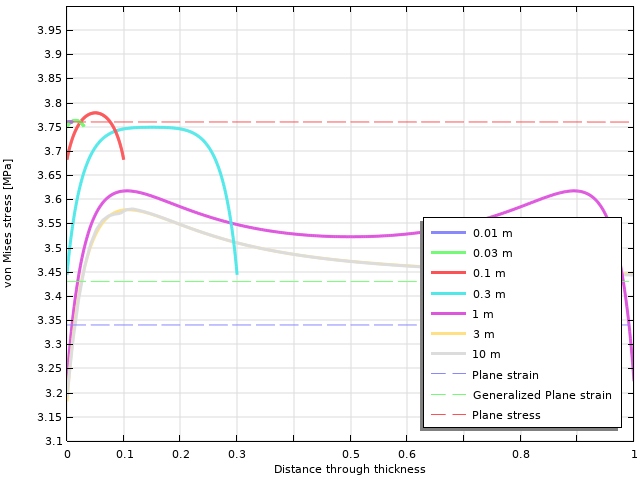
Von Mises 等效应力随着厚度的变化。图中的参数为物体的厚度。
对于较厚的物体，实际等效应力与任意一个二维解均存在显著差异。只有在相当厚的物体内部，von Mises 应力才会收敛于广义平面应变解。
非弹性应变
在大多数情况下，这三种公式之间的区别不像在上文示例中那样明显，即存在有一个显著的应力集中。然而，在某些情况下，必须特别注意:当非弹性应变很重要的时候。因此，在横向上不仅泊松比对面内应变起作用。
以热膨胀为例。通常在各个方向的热膨胀都是一致的。这意味着在平面应变设置中（面外膨胀被抑制），将会有一个强大的横向应力累积。一个可以在 xy 平面自由膨胀的物体将受到一个横向应力，\sigma_z = -E \alpha \Delta T。如果选择使用平面应力或广义平面应变公式，横向上的膨胀是自由的，这个应力将不会出现。
为了说明二维公式在热膨胀情况下的重要性，我们来看以下示例: 一个在 xy 平面自由膨胀的正方形板受到温度场的影响，其中温度与 x*y 成比例。右上角的最高温升为 100 K。材料数据为钢。横向应力如下图所示。
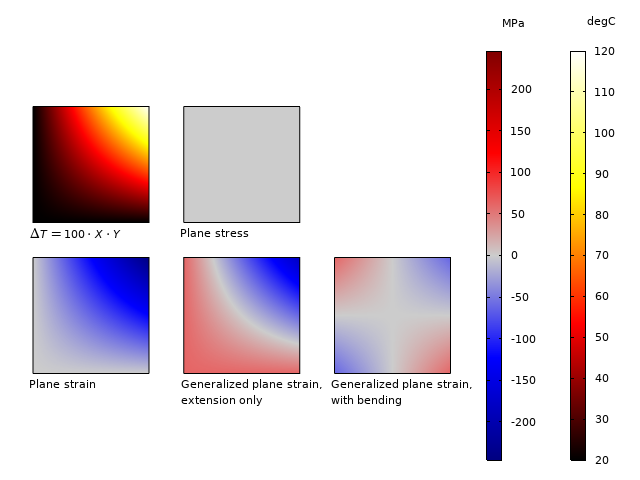\sigma_z不同二维假设下的温度分布和面外应力。
结果表明:
- 在平面应力情况下，面外膨胀是自由的，因此不会产生应力。
- 对于平面应变，整个截面受到压应力的值为 \sigma_z = -E \alpha \Delta T(x,y)。应力范围为 -245~0 MPa。
- 对于仅有拉伸的广义平面应变，增加一个恒定应力以使平均 \sigma_z 变为零。应力范围为 -184~61 MPa 。
- 对于包含弯曲的广义应变，还增加了一个线性变化的应力场。应力范围为 -61~61 MPa。
关于等效应力的说明
von Mises 等效应力和 Tresca 等效应力是最常用的 2 个标量应力测量。如果用主应力（\sigma_1 > \sigma_2 > \sigma_3) 表示,则为
和
可以看出，中间主应力影响 von Mises 等效应力，但不影响 Tresca 等效应力。对于二维情况，面外应力分量 \sigma_z 始终是主应力之一。对于平面应力情况，面外应力分量为零。对于平面应变情况，线弹性材料的面外应力分量为 \sigma_z = \nu \left ( \sigma_x + \sigma_y \right ) = \nu \left ( \sigma_{1 \mathrm p} + \sigma_{2 \mathrm p} \right ) ，。最后一个表达式包含两个面内主应力。如果 \sigma_{1 \mathrm p} 和 \sigma_{2 \mathrm p} 的符号不同，则 \sigma_z 始终是中间主应力，Tresca 等效应力不受平面应力和平面应变变化的影响。
由于 von Mises 等效应力取决于中间主应力，因此这种不变行为在 von Mises 等效应力中看不到。
平面应力与平面应变条件下的等效应力值之差。Tresca 等效应力 (上)和 von Mises 应力 (下)。注意，在 Tresca 等效应力情况下，大片黑色区域为零差异。
关于断裂力学的说明
在断裂力学中，常用平面应变假设来分析厚板。既然我们已经知道了广义平面应变或全三维是正确的选择，为什么这种假设又是可行的呢?
对于这种情况，重要的是看裂纹尖端的状态。裂纹尖端处的应变状态是奇异的，因此材料在厚度方向上有很强的收缩倾向。周围材料抵抗这种收缩，形成对厚度方向位移的强烈约束。因此，接近裂纹尖端的应力状态类似于平面应变。实际上，平面应变解和广义平面应变解在接近裂纹尖端处的结果相当一致。这并不是说平面应变在平面裂纹体中是一个很好的近似。实际上，平面应变解在一定程度上低估了整体变形。在大多数板中，应力梯度很小，平面应力是一个更好的近似。
一维理论
通常使用梁或桁架来近似模拟细长结构。对于这类情况，使用单轴理论定义。横向应力和应变并不直接参与问题的计算。不过，如果研究一下细节，就会发现一个基本假设，即横向没有应力。从本质上讲，两个（任意）正交方向存在平面应力条件。如果需要，可以计算 后验 横向应变。对于线性弹性材料，可以直接使用泊松比的定义；横向应变为 \varepsilon_T = -\nu \varepsilon_A，其中，\varepsilon_A 为轴向应变。
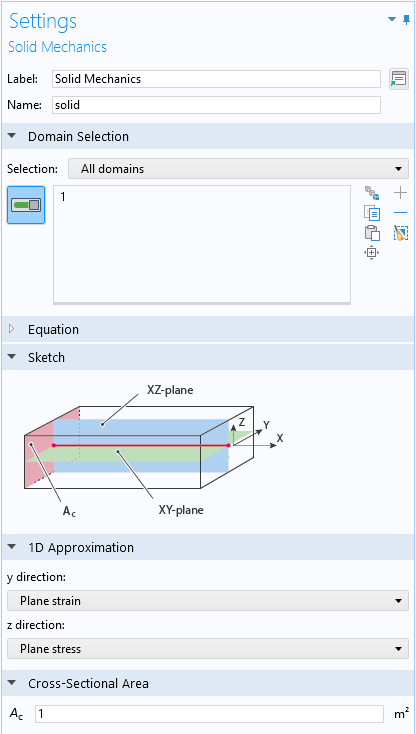
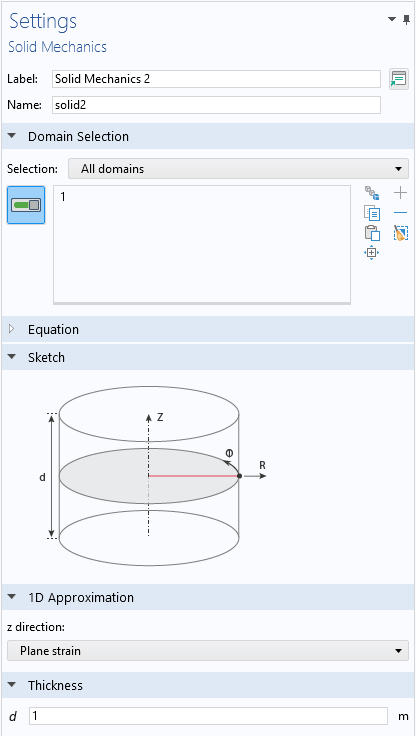
从 COMSOL Multiphysics 6.1 版本开始，固体力学 接口也可用于一维和一维轴对称几何。此处，还必须确定面外行为。在一维情况下，可以在两个横向方向上独立选择平面应力、平面应变和广义平面应变。在一维轴对称情况下，厚度方向的行为也包含这三个选项。
一维和二维轴对称情况下 固体力学 接口的部分 设置窗口。
下一步
结构力学模块是 COMSOL Multiphysics 的附加产品，包括用于模拟平面应力和平面应变的专用特征和功能。点击下方按钮，了解更多关于结构力学模块的信息:
评论 (0)