
上一篇博客,我们讨论了生成高质量网格的因素以及如何建立 CFD 模型几何结构来进行网格划分。本文,你将了解物理场控制的网格划分,自适应网格细化以及如何在 COMSOL Multiphysics® 软件中使用不同的网格划分技术执行流体流动仿真。
物理场控制的网格划分序列
在 COMSOL Multiphysics 中,设置完流体流动模型流动条件后,我们就可以调用物理场控制的网格划分序列。这种序列取决于以下几方面:
- 物理属性设置
- 例如,带自动壁处理功能的湍流模型可以生成比层流模型更细的网格
- 特定的特征
- 例如,壁可以产生更细化的网格和边界层网格
- 几何结构的边框大小
- 可以控制单元的大小比例
Ahmed 类车体模型(我们在之前的博客中也使用过)中物理场控制的网格划分序列如下图所示:

在网格1 节点下:
- 大小 子节点包含一组网格大小参数,这些参数取决于属性设置和几何结构边框
- 大小 1 子节点在所有无滑移壁上都处于激活状态,并在这些壁上指定了更细的网格
- 角细化 1 子节点自动识别无滑移壁内所有足够尖锐的角,并沿着这些边指定更细的网格(在这个示例中,除了连接车顶和斜面的边外,该节点会找到车体上的大多数锐边)
- 自由四面体网格 1 子节点在两个边界上和域内创建实际网格
- 边界层 1 子节点将边界层网格添加到所有无滑移边界
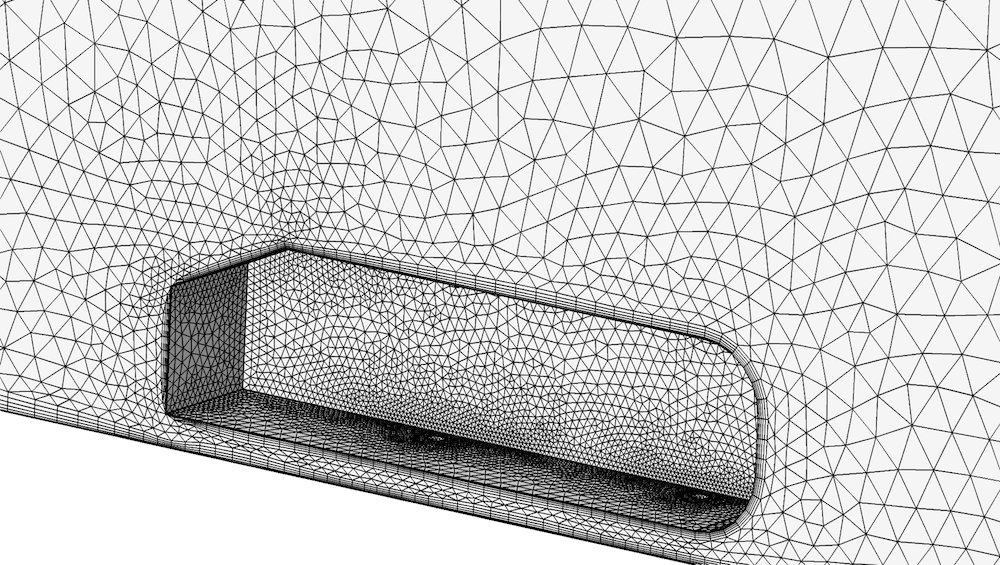
Ahmed 类车体模型的物理场控制的网格划分序列产生的网格的放大视。可以看到,壁上的网格较体内的更细,靠近锐边的网格甚至更细。还可以看见无滑移壁上的边界层网格。
有时,物理场控制的网格对简单的模型已经足够了并且是进行更高级的网格划分的起点。使用上图所示的网格完全有可能求解 Ahmed 类车体问题。然而,我们看到,车体后部的网格控制的域没有产生任何更细的网格,非结构化网格覆盖了整个风道。因此,车体后方的网格可以更细,而车体下方的网格则没必要细化。利用车体后方的网格控制的域和本系列博客第一部分中所示的分割面,单元总数可以大致保持不变,但会获得更高的分辨率。
COMSOL Multiphysics® 中 CFD 仿真的网格划分技术
COMSOL Multiphysics 中有多种不同的技术可用于控制和生成网格。我们先讨论用于表面网格划分的技术,因为先对表面进行网格划分可验证分辨率足够高和单元质量足够好。请注意,为特定尺寸的实体划分网格的技术也可以为相邻的较小尺寸的实体划分网格。例如,自由三角形网格 特征可以为其指定的面划分网格,也可以为所有相邻的、之前未划分网格的边和点划分网格。因此,在为面划分网格之前,无需为所有边划分网格,并且在没有为所有闭合面划分网格的情况下也可以为体划分网格。
映射网格
映射具有创建最佳表面网格的潜力。下图显示了太阳能电池板模型中一块电池板的高质量映射表面网格。细化映射网格以在自由边附近获得更细的单元,并平滑过渡到覆盖所有梁的细化网格。使用 分布 节点获得各向异性,该节点包含若干设置,可控制单元数量以及这些单元沿边分布的情况。事实上,所有单元都有 90° 角,这意味着单元完全没有偏斜。
映射网格对于二维仿真特别有用,例如下图所示的 NACA 0012 机翼基准模型。此模型中的映射网格最显著的特性是它对单元大小、质量和增长率的极佳控制,即使它可能需要一些操作来指定所有边上的最优分布。

NACA 0012 机翼模型的二维映射网格。
非结构化四边形网格
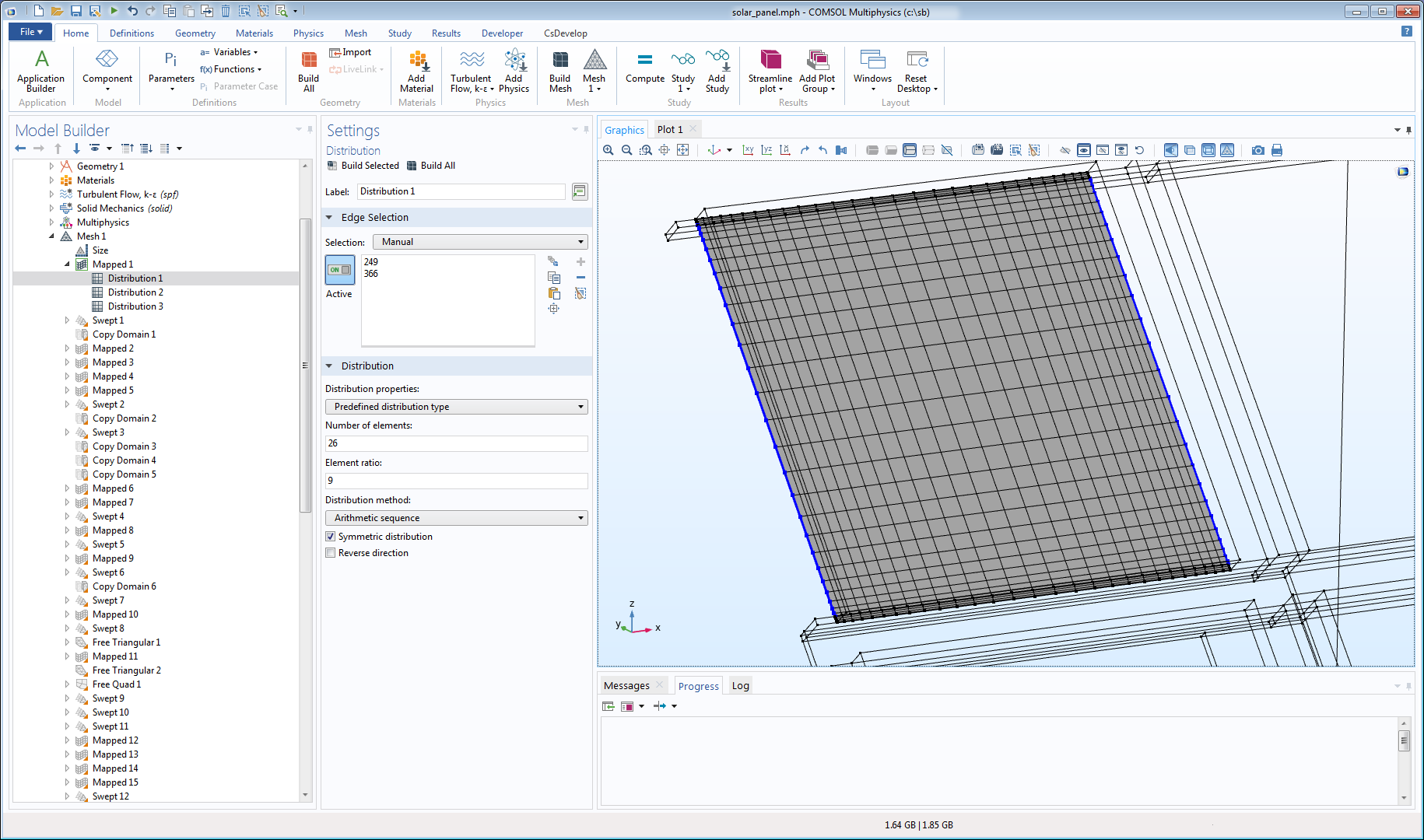
将有些表面划分为可映射的面非常麻烦。对于这种情况,我们可以使用 自由四边形网格 节点。下图示例显示了由非结构化四边形网格划分的支架面。面上的最大单元大小由 大小 属性控制,而 分布 属性则用于控制沿多个边的分布情况。
这个面也可以通过自由三角形网格操作划分网格,但那样会产生更多的单元。还可以看出,从相邻的映射网格测量的增长率并不是最好的。支架位于太阳能电池板的下侧,对流动的影响较少,因此网格主要影响模型的结构力学部分,对于这部分来说,增长率并非关键因素。
三角形网格
自由三角形网格操作是二维 CFD 模型的“主力”,因为通过这种方法可以快速、简便地获取覆盖整个几何结构的高质量网格。轻松创建非结构化网格需要一定的计算代价。非结构化三角形网格比结构化网格产生更多的数值扩散。这意味着在使用非结构化网格获得的解比使用大小相当的结构化网格获得的解更模糊。此外,非结构化网格在没有偏斜的情况下不可能具有高度各向异性。
一般来说,求解CFD 问题的非结构化网格必须比结构化网格细很多才能获得同等水平的精度。不过,有时可能需要额外的扩散,因为这种情况更容易收敛。对于下图所示的超音速喷射器模型来说,这是一个理想选择。在该模型中,非结构化网格用作网格自适应的起始网格(如下图所示)。
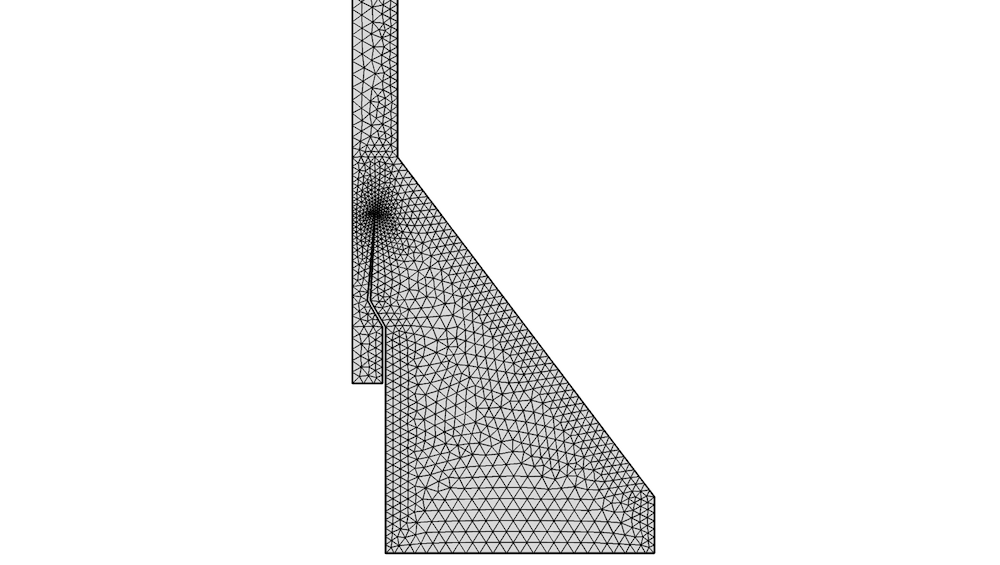
超音速喷射器二维轴对称模型的三角形网格。
自由三角形网格划分操作在三维模型中很少使用,其主要用途是对各个面进行“网格划分测试”,尤其是那些我们已经对其应用虚拟操作的面。我们可以研究各个面上的网格质量,而无需为相邻的体划分网格。非结构化三角形网格也可以用作扫掠网格的起点。这种策略会产生包含棱柱单元的网格,棱柱单元的二次边可以被拉伸,从而产生各向异性网格。
四面体网格
几乎所有工业级应用的几何结构都包含一个或多个不适合扫掠的域,从而必须用四面体网格来覆盖。自由四面体网格划分操作会在构建体网格之前,先在未划分网格的面上构建表面网格。表面网格必须与几何结构边界一致,但是在单元质量优化期间,表面网格 节点可以在面内移动,而已划分网格的面仍保持不动,因此可能会产生质量较低的单元。
四面体只有三角形边,因此需要使用某种单元来实现从包含四边形单元面的过渡。这种单元就是金字塔单元,它形式上是六面体单元,其中一个单元面折叠为一个点,留下包含一个四边形面和四个三角形面的单元。太阳能电池板模型中有许多包含四边形单元的面,因此需要使用金字塔单元过渡到太阳能电池板周围域中的非结构化网格,如下图所示。
我们经常听说金字塔单元不如其他类型的单元,但金字塔单元本身 并不差。当金字塔位于各向异性四边形上时,其底部必须具有相同的各向异性。金字塔形状的任何微小扰动都会产生偏斜度相当高的单元。如下图所示,位于面板边上的高度各向异性四方形面顶部的金字塔单元通常比面板中心的金字塔单元质量低。在这种情况下,与其在面板中使用非结构化网格,不如整体上使用大小小得多的低质量网格。
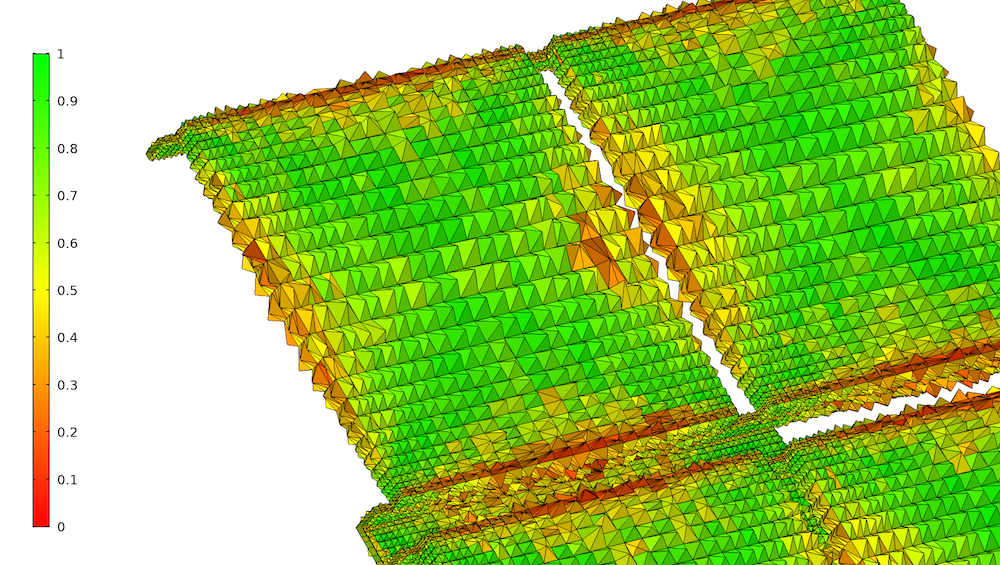
位于太阳能电池板几何结构的四边形单元顶部的金字塔。这些单元根据质量着色,质量根据偏斜度计算得出。
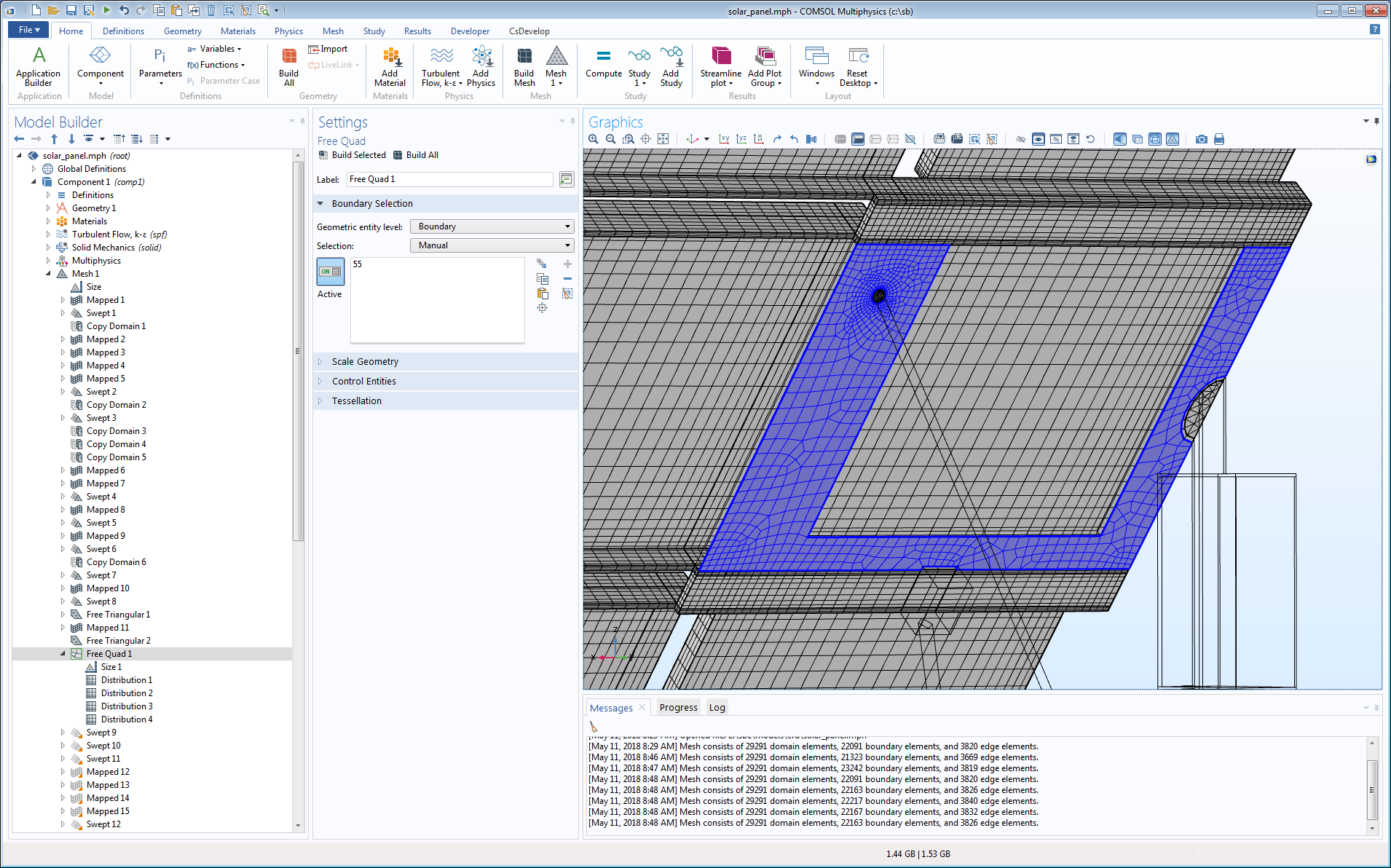
通过使用网格控制域,可以显著改善对自由四面体网格操作生成的网格的控制。对于下图示例,大小 3 属性在 Ahmed 类车体的斜面和背面指定了一个小型最大单元大小。自由四面体网格 1 的大小 1 属性在网格控制域中制定了一个较低的增长率,这导致在尾流区内产生增长率低且单元质量高的细网格。当划分完周围的空气域网格后,包含网格控制域的边界将被移除,我们就可以自由添加边界层网格并移动相邻的单元。
我们可以考虑对上面的网格控制域使用扫掠网格。但这样做会使向其余非结构化网格的过渡变得更加困难,而且实际情况也不会有所改善,因为我们预计“车体”后部的旋涡流动是相对各向同性的,这意味着结构化网格也需要具有一定程度的各向同性。
扫掠网格
在 COMSOL Multiphysics 中,映射网格的三维网格用扫掠网格表示。对一组源面进行扫掠;为源面划分网格并将它们投影到多个目标面上;然后根据源网格包含三角形单元还是四边形单元,使用棱柱单元或六面体单元连接这些面。扫掠操作非常适用于获取在流线方向被拉伸的网格,同时在横截面上保持给定的分辨率。
下图示例中,在 Ahmed 类车体模型风道的下游区域添加了扫掠网格。细心的你会发现,非结构化四面体网格与靠近顶面的扫掠网格之间的增长率可能会更好。但此处的流场几乎没有变化,因此在“车体”后方获得良好的增长率更为重要。
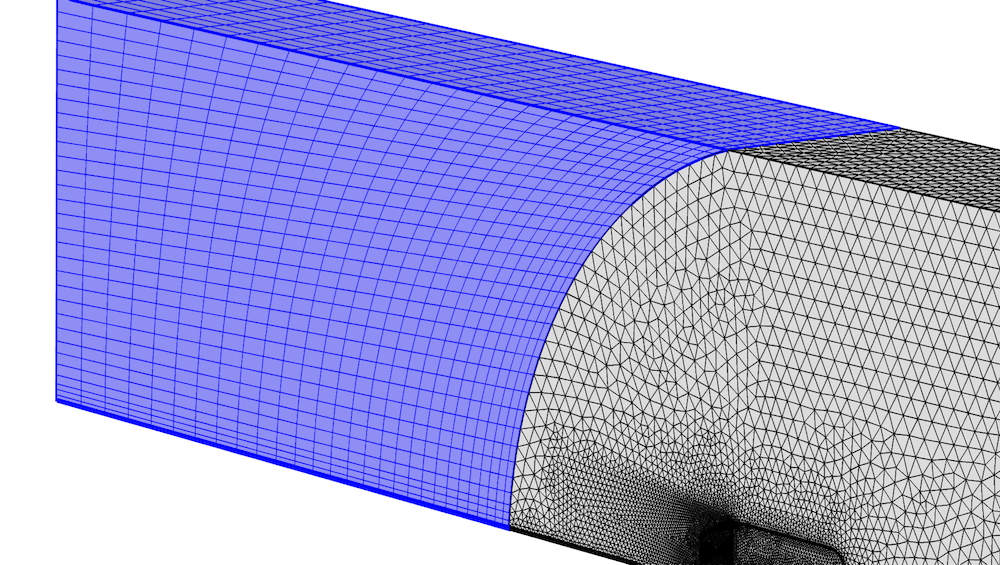
Ahmed 类车体下游的扫掠网格。
上述扫掠网格使用自由四面体网格操作和边界层操作得到的面网格作为其源网格,这通常是一个非常有用的方法。我们可以在出口边界上创建一个非结构化三角形网格,并将网格从出口向上扫掠至曲面。不过,这将限制自由四面体网格操作(参见三角形网格部分)。我们不仅需要在包含非结构化网格的部分创建边界层网格,将这些网格扫掠至下游,还需要沿着整个风道底板推进边界层单元。
边界层网格
边界层网格划分是 CFD 仿真的重点,此操作可以在壁附近创建高度各向异性的网格,而无需使用扫掠网格或特别指定的域。如之前的博客所述,边界层通常在无滑移壁上形成,因此这些单元是必需的。
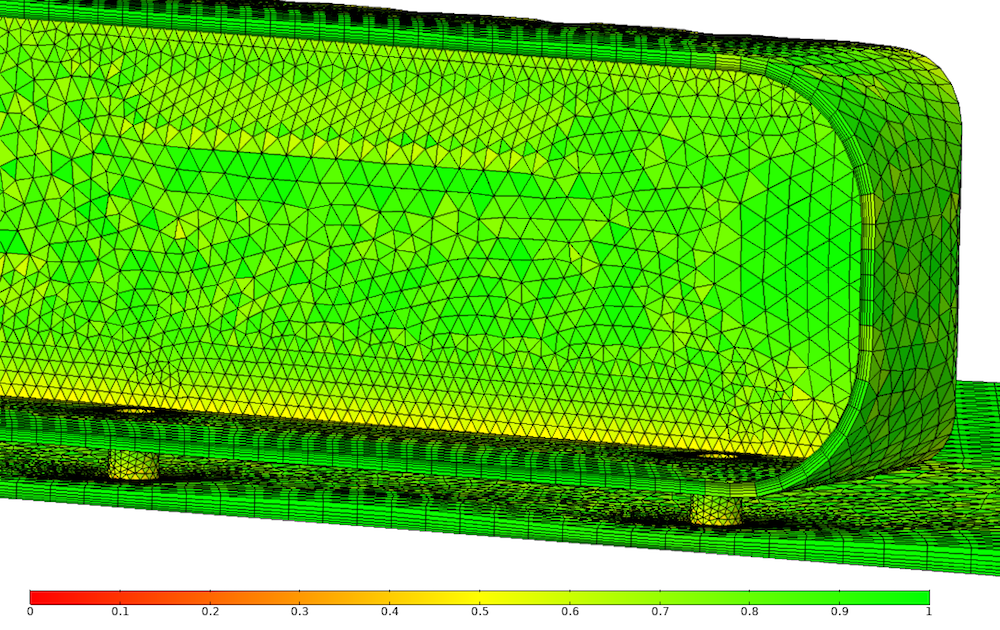
Ahmed 类车体模型的边界层网格。单元根据质量着色,质量根据偏斜度计算得出。
在 COMSOL Multiphysics 中,需要在为域划分网格之后添加边界层网格。各向异性棱柱或六面体单元被推入计算域,产生如下所述的多个高度的各向异性单元。结果表明,尽管这些单元呈各向异性,但质量良好。因为在这种情况下,边界层网格在这种情况下由高质量的三角形构建,同时产生了高质量的棱柱单元。
边界层网格特征
边界层网格有三个特征:
- 第一层单元的高度
- 增长率
- 层数
首先是第一层单元的高度,它通常指定为面单元长度尺度的一部分。典型的默认值是面单元的长度尺度比第一个边界层单元的高度大 50 倍。更高的宽高比可能会给出更高的分辨率,但最终的方程组也可能更难求解,尤其在使用迭代求解器求解时。
第二个特征是拉伸因子,即从第一个单元层到下一个单元层的增长率。这对于得到向非结构化网格的良好过渡非常必要(如上文所述)。顶部边界层过渡到非结构化网格时,单元大小的激增显而易见。边界层可以在边界层网格中采用更大的拉伸因子,也可以采用更多层(层数是边界层网格的第三个特征)。但上述边界层网格的厚度不能再增加了,原因是,为避免非结构化网格高度偏斜,车体与地板之间的间隙中的网格已被严重压扁。边界层网格的压缩通过底层算法自动完成。
选择第一层单元高度、增长率和单元数是一个折衷的方法,可以在必要的分辨率、向非结构化网格的良好过渡以及最终单元质量之间取得良好的平衡。
锐边的特殊注意事项
如果你亲手包装过礼物,就会知道包装纸在尖锐的边周围收紧时很容易被撕破。边界层网格也存在类似的问题,如下图所示。后缘锐边处的边界层网格单元偏斜的厉害,就像机翼下游的单元一样。
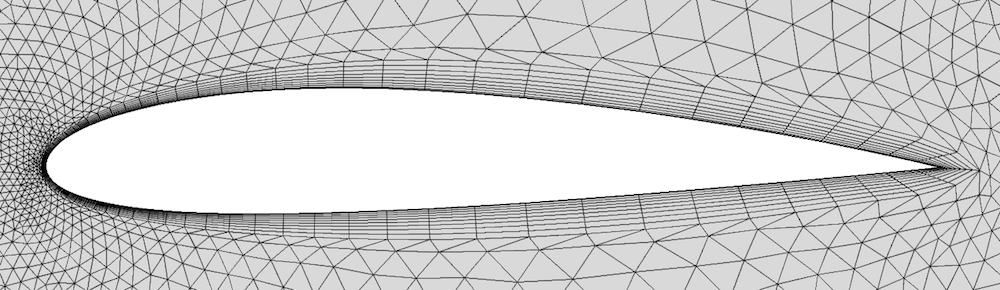
未经特殊网格处理的机翼后缘的锐边。
一种选择是在锐边上“拆分”边界层,结果如下图所示。现在,边界层网格尾端是两个特殊的单元列,这两列都以三角形单元开头,后面均为适当数量的四边形单元。通过拆分操作可以控制角的锐度,以及每个“特殊”单元列应覆盖的最大角。优化这些参数可以明显提高锐边处的单元质量。
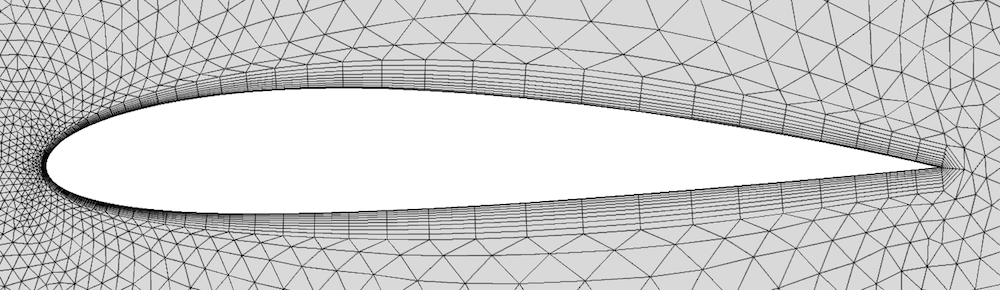
在机翼锐边处拆分边界层
然而,拆分操作并非适用于任何情况。在复杂的三维 CAD 几何结构中,任何数量的边都可以连接到锐角,这种几何结构拆分起来尤其困难。必需针对每个拓扑位移的配置为算法进行编程,并且高级几何结构很可能至少包含一个算法无法处理的锐角。
此外,也可以使用第三种锐角处理方法,即 修剪,这是 COMSOL Multiphysics 中处理锐角的默认选项。机翼的处理结果如下图所示。由于层靠近锐边,每个靠近边的单元的高度都降低了两个单元。这种方法也可以视为边界层单元数从锐边开始的增长。为了获得最佳网格,可以同时控制增长的单元数和修剪的最小角。
与不做处理或不拆分相比,修剪操作可以降低锐角处的有效分辨率。因此应该始终将修剪与网格的一般细化结合使用,这也是上面讨论的 角细化 特征默认包含在物理场控制的网格序列中的原因。
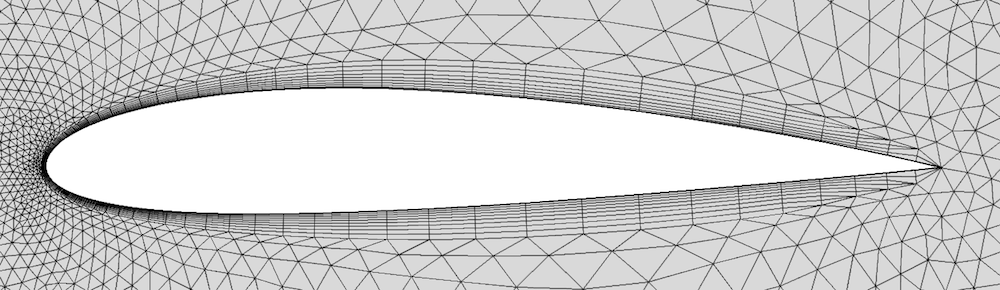
为包含锐角的边界层划分网格时,修剪是默认选项。
边界层网格可以提高狭窄区域的分辨率。仔细观察上图中的网格可以发现,车体与地板之间的区域被 15(6+3+6)个单元覆盖。这足以表征可能在这一狭窄区域中发生的任何速度分布。如果没有边界层网格,间隙将仅被 3 个单元覆盖,这严重限制了网格表征 Ahmed 类车体下方流动剖面的能力。流动通常会被人为节流,使窄区域在数值上比几何上显得更窄。因此,边界层网格不仅可用于湍流边界层,也可用于层流甚至微流体系统。一个好的经验法则是:必须使用至少5个单元来解析狭窄区域。
复制网格
最后,我们将介绍如何在各个实体之间复制网格。只要源网格可以通过平移、旋转和各向同性缩放映射到目标实体,就可以在相同尺寸的实体之间复制网格。这意味着目标实体必须与源实体形状相同,但目标实体可以位于另一个位置,以某种方式旋转并且可以具有不同的大小。
复制网格对于映射网格和扫掠网格特别有用。通过复制网格,我们可以用一个复制操作代替多次映射和扫掠操作,以及多次分配属性操作。如之前的博客所述,如果几何结构被正确分割,就可以实现复制网格。这样一来,只需更改源域的序列,就能够在创建网格时提高工作效率,还可以更轻松地管理网格的任何后续更改。复制操作会自动将这些更改传递到目标域。
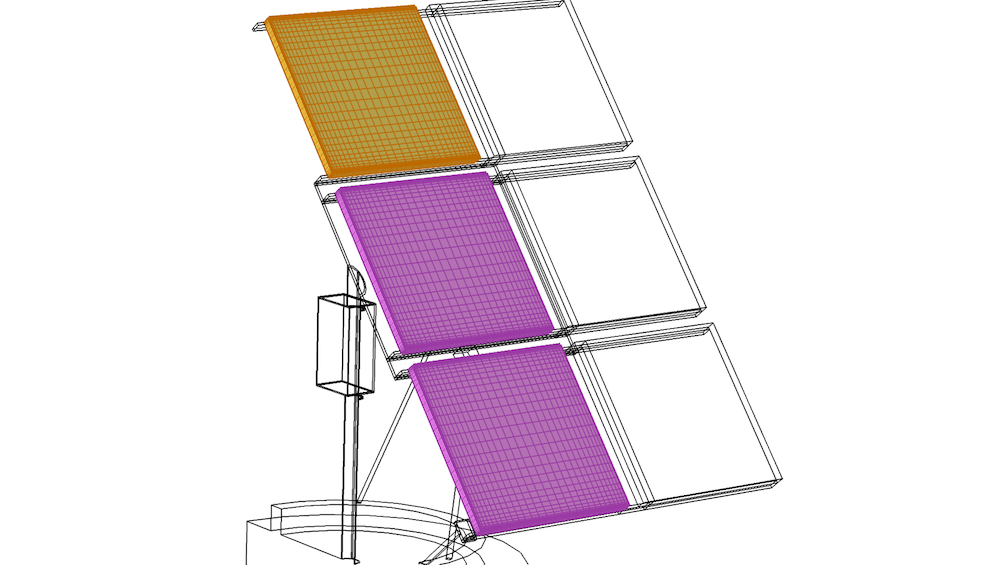
黄色域中的扫掠网格被复制到两个粉色域。
自适应网格划分
在模拟 CFD 问题时,我们力图在梯度较大的区域中创建密集网格。不过,有时很难预测梯度骤变出现的位置。还有一些瞬态情况,骤变的梯度会移动。这可以通过在出现梯度骤变的区域创建细化网格来解决,但通常计算成本会很高,较好的解决方法是采用自适应网格划分。
稳态问题的自适应
在由跨音速流在壁挂式凸起物上产生的激波系统的等压线就是自适应网格划分的一个例子。激波可以通过稳定性方案捕获,但粗化网格会使它们显得模糊不清。

壁挂式凸起物上欧拉流动的等压线。
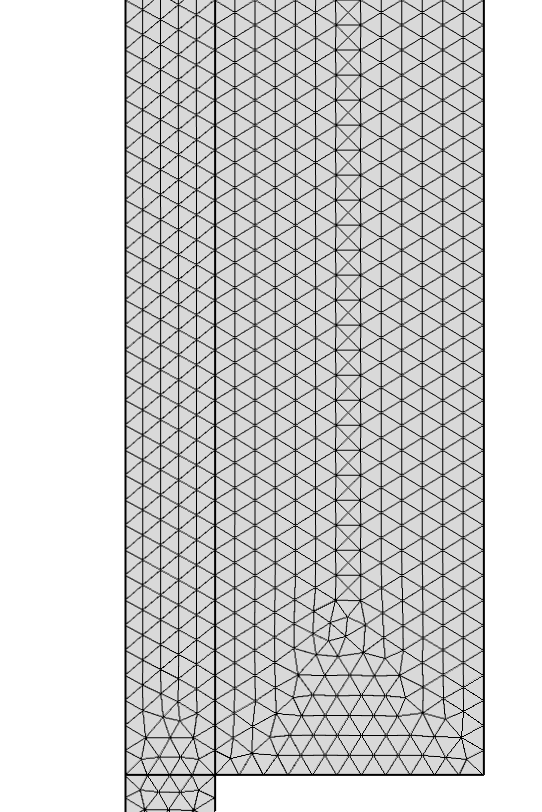
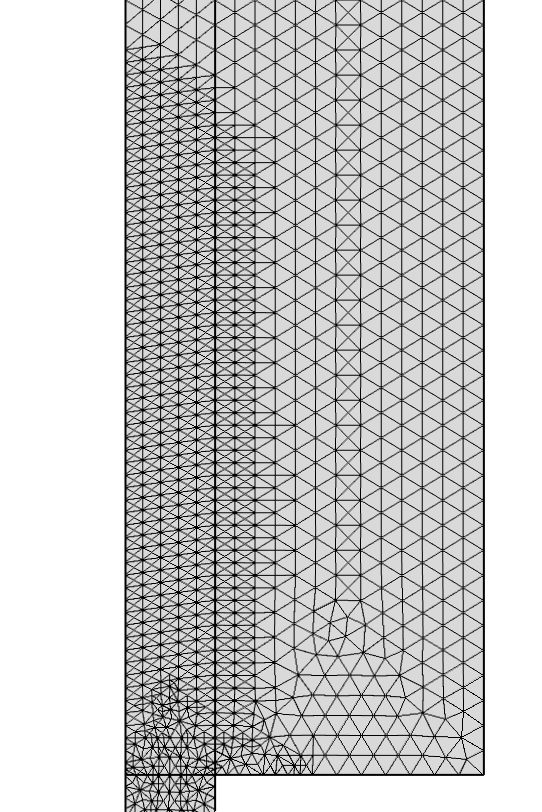
上图中的强激波是从一个均匀的、相对粗化的网格开始的(如下图左所示)。基于粗化网格得到的解可用于粗略估计方程残差,并在残差较大的位置细化网格。方程基于最终的较细化网格进行求解。你可以重复此过程,直到获得满意的精度。
上述用于计算压力场的网格如下图右所示,这是非常简单的初始网格经过两次自适应细化后的结果。由于问题必须在初始网格上收敛,因此自适应仍然需要一些操作来创建初始网格。
欧拉流动模型的初始网格(左)和自适应网格(右)。
瞬态模型的自适应
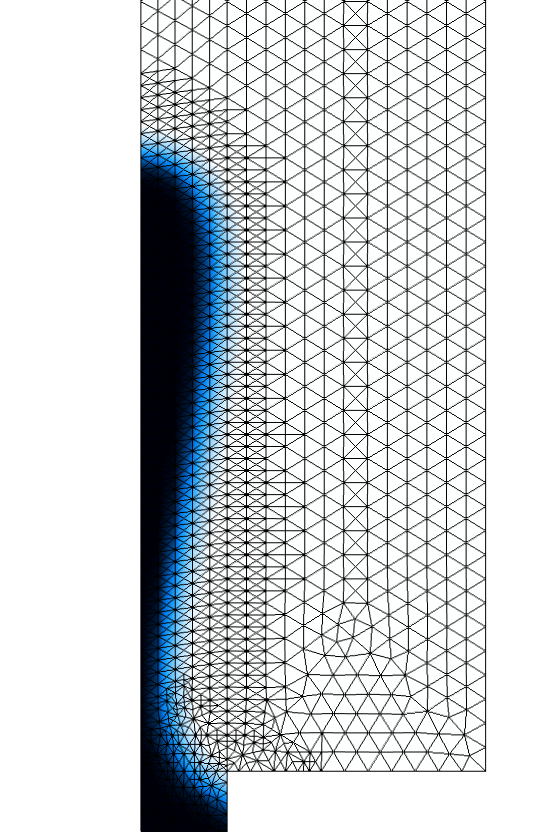
瞬态模型的自适应方式略有不同。基础粗化网格用于在一定时间间隔内推进求解。随后使用求解结果基于某个指示函数来细化网格,并使用自适应网格再次模拟时间间隔。下图左显示了喷墨打印机喷嘴模型的基础网格,中间的图显示了自适应网格。由于这是一个两相模型,因此自适应基于\|\nabla \phi\|进行,其中\phi是水平集函数(0 位于一个相,1 位于另一个相)。右图显示了自适应时间间隔结束时的解。可以看到,细化网格在整个时间间隔范围内覆盖界面前方的传递。
喷墨打印机喷嘴的瞬态网格自适应。
瞬态自适应网格划分是一种非常经济有效的方法,可以得到非常好的结果。这种方法的效益很大程度上取决于基础网格,基础网格不可能太细,因为问题必须在基础网格上多求解一段时间。对基础网格执行一些操作,通常会获得不错的效果,对于较高级的几何结构来说尤其如此。
CFD 模型网格划分工具总结
为 CFD 模型创建合适的网格是一门艺术。即使使用自适应网格划分,要获得高质量的网格,也需要理解各种网格划分技术如何工作,以及预测流动问题的预期解。
我们创建的第一个网格通常不够理想,往往需要改变几何结构、网格,或同时对二者进行修改。COMSOL Multiphysics 中的几何结构和网格划分序列可以很好地应对这一问题。几何序列中引入的变化可通过模型向下传递,如此一来,在几何结构中引入变化时,就无需重新指定物理场或网格设置。此外,我们也可以大幅更改网格设置,重建整个网格序列,而不用从头开始操作。另一种可能是在几何结构和网格中使用参数,从而得到一个模型,单击几下鼠标即可将网格细化。
本系列博客只是粗浅地介绍了在 COMSOL Multiphysics 中创建网格的可能方法。除这些方法之外,你还可以使用更多设置和选项进行 CFD 仿真。
后续操作
延伸阅读
请阅读以下 COMSOL 博客文章,了解有关网格划分和 CFD 仿真分析的更多内容:








评论 (1)
gaofeng lu
2019-04-15