
故事始于阿基米德正在处理的一桩金皇冠诈骗案。当他洗澡的时候突然有了灵感:将一个物体浸入水中,所排出的水量与该物体的体积相同,这样他就可以查出掺有杂质的黄金了。阿基米德高兴地大喊:“找到了(eureka)!”但是会有人会听到这著名的呐喊吗?通过仿真,我们可以评估共振和混响封闭空间(如浴室)的声学效果,及其对基源的响应。
共振和混响空间背景
当阿基米德喊出“找到了”时,如果他的声音波长与浴室的尺寸相匹配,就会产生共振。发生共振时,声音的振幅会变得非常大。在封闭的空间中,不同的频率下会有许多共振或声学空间模式,每种模式都有节点和波腹:节点的声压为零,而波腹位于声压最大的地方。

阿基米德在浴缸中高喊“找到了”,据说他在浴缸中创造了这个词。图片由 John Leech 通过维基共享提供,不受专利权限制。
共振通常与较大的响应相关联。然而,如果单极子位于节点上,则不会产生噪声;单极子位于波腹上时效率最高。相反,如果偶极子位于一个节点上,它将不会发出声音;但如果偶极子位于波腹上,并且垂直于波腹方向,则会产生强烈的响应。你可以通过嘴巴进行频率扫描(也被称为在淋浴时唱歌)来找到自己浴室的共振模式,同时倾听并寻找某些音高的音量是否意外增大。
混响空间存在许多声波反射,这些声波在边界处没有被有效吸收。混响与回声相似,不同之处在于不同回声之间可以明显区分。混响对空间中的语音清晰度有很大的影响:混响时间越短,声音效果就越清脆、越清晰、越干净,而像大教堂这样的空间,声音就会很浑浊。你可以通过拍手并计算能够听到的噪声衰减时间来对混响空间进行试验。
利用 COMSOL Multiphysics® 预测共振
研究封闭空间声学的第一步是绘制浴室的几何图形。在这里,浴室被改造成一个 2m × 5m 的矩形,中间有一个点。首先,我们要找到最初的几个振型和频率。一旦这些被建立起来,就可以将单极子和偶极子被放置在一个节点和波腹上从而研究响应。
本征频率预测
将压力声学、频域接口应用于矩形,方程的频域形式为稳态亥姆霍兹方程。矩形的边界条件与默认的声学刚性边界;因此,该模型是无损的。几何图形和接口如下图所示。
第一项研究解决了域的本征频率,这些本征频率对应于矩形的声场模式。请注意,当求解特征频率时,任何应用于模型的源都将被忽略;即,它是方程齐次形式的根。空间模态由域的长度和边界条件决定,可以通过推导的解析解来验证这个典型问题的数值近似解。
下图显示了封闭空间的前两个振型。图中显示波腹和节点分别位于第一和第二振型的 x = 0 线上。该几何图形的两种模态频率分别为34 Hz 和 68 Hz。但实际的频率并不重要,所以在这篇博文中不会被直接引用。
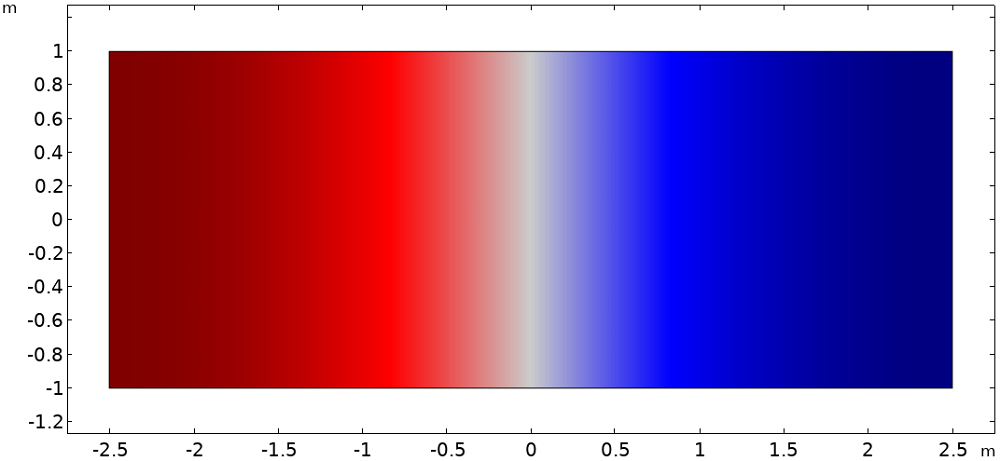
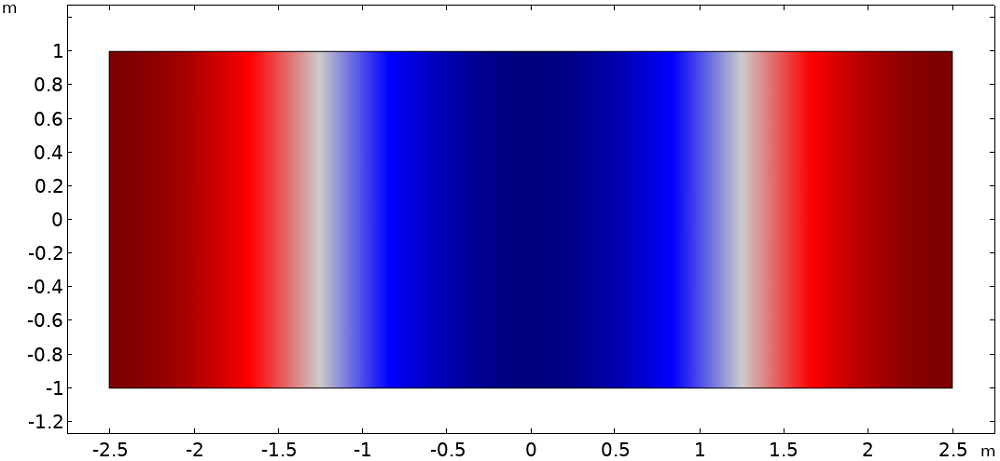
封闭空间前两个振型的归一化压力。第一种振型(左)在中间点有一个波腹,而第二种振型(右)有一个节点。
封闭空间的基源
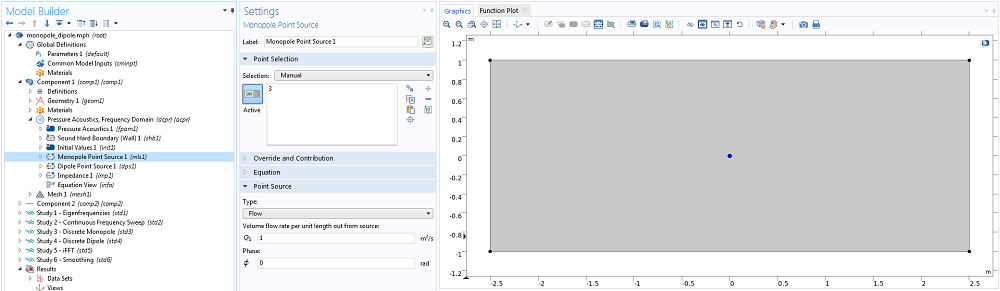
在确定了振型和相关频率后,下一步是将单极子和偶极子添加到几何图形中心的点上,偶极子沿 x 方向。在两个频域研究步骤中,单极子和偶极子在适当的频率范围内被激发。在后处理过程中对结果进行归一化处理,使两个源都具有单位振幅。
为了评估封闭空间对基源的影响,对声压级(sound pressure level, SPL)进行平均处理。为了实现这一点,将平均 组件耦合应用到域中,该耦合算符可以计算变量的空间平均值。
不同的基源在封闭空间中的平均 SPL 如下图所示。图中显示,在任一模式下,每种源的平均 SPL(超过 80 dB)都有很大的增加。结果表明,单极子在第一种模式下影响不大,但当位于波腹上时,其响应很大。偶极子的响应是相反的。对于简单的模型,这一结果可以通过分析预测得到证实。
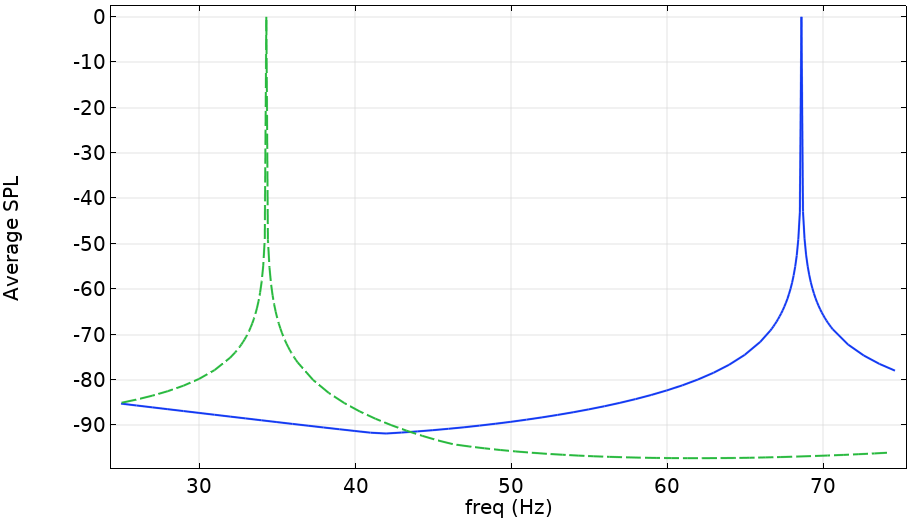
两种基源的平均 SPL。蓝线是单极子,绿色虚线是偶极子负载。两个源都位于封闭空间的中间位置。
或者,源可以按本征频率的精确值加载。这可以通过在接口的设置 面板下将方程形式从研究控制 更改为频域 来实现。然后可以使用 withsol('sol1',real(freq),setind(λ,N) ) 指定应用频率。这意味着:使用 (withsol ) 解 1 ('sol1'),并将频率 (real(freq) ) 设置为指定索引( N 等于 1 和 2)的特征值 (λ)。因为该模型是无损的,所以需要 1e-3 Hz 的偏移量,并且在共振时很难在数学上定义,因此不会返回解。
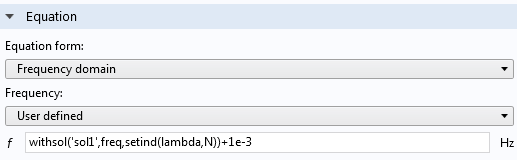
在 COMSOL Multiphysics 中以精确的本征频率加载模型所需的编辑步骤。
实施这种方法时,两种基源中一种模式的平均 SPL 要比另一种模式低约 87 dB。
关于封闭空间共振预测的思考
通过对共振模型的分析,我们可以得到:如果阿基米德和他的浴缸是无穷小的,位于波腹上,并且具有单极子噪声方向性特征,那么当阿基米德大喊“找到了”时,几乎没有人会听到。
模拟封闭空间中的混响
封闭空间的混响可以通过模拟瞬态基源和测量随时间变化的 SPL 来量化。单极子可以用扬声器的球面阵列来近似描述。建筑声学专家常用的度量标准是测量一个房间的 T60 值——声场衰减 60 dB 所需的时间。
射线理论可以用来预测封闭空间的脉冲响应,但这种近似仅在高频极限下有效,不适用于声学上小而封闭的空间(如阿基米德的浴室)。幸运的是,有限元法(finite element method,FEM)可以用来计算低频响应,然后这个低频响应可以传递到一个快速傅立叶逆变换(inverse fast Fourier transform,iFFT)程序中,生成由基源或分布源引起的低频脉冲响应。
单极子的低频响应
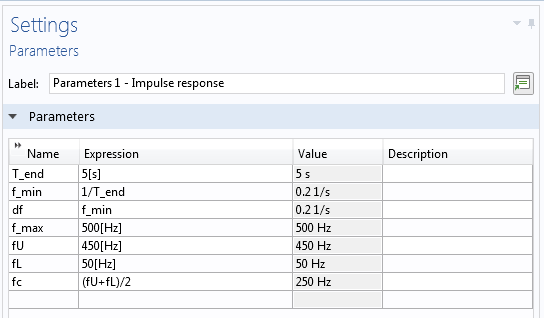
当获取脉冲预测时,下面左图中显示的参数可以加快建模过程。
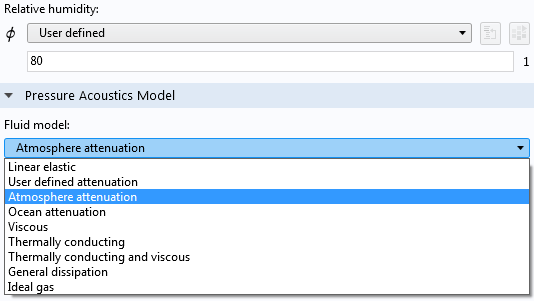
混响模型中使用的参数(左)和衰减模型(右)。
流体模型 从默认的线弹性 (不含损耗)变为大气衰减。这种衰减模型基于半经验模型。因为温水浴作用,将相对湿度设置为较高值 80。此外,边界改为微损耗阻抗边界。
偶极子被禁用,按参数给出的频率加载单极子。本研究分两步进行,第二步取值研究 1 的频率响应结果,并对窗口结果进行 iFFT。下面的动画显示了由于单极子以 250 Hz 的中心频率振荡而产生的总瞬时压力。在这个频率下,很明显波长不在这个长度的几何图形的高频限值内。
单极子源在域中心 250 Hz 时的瞬时压力。
脉冲响应预测
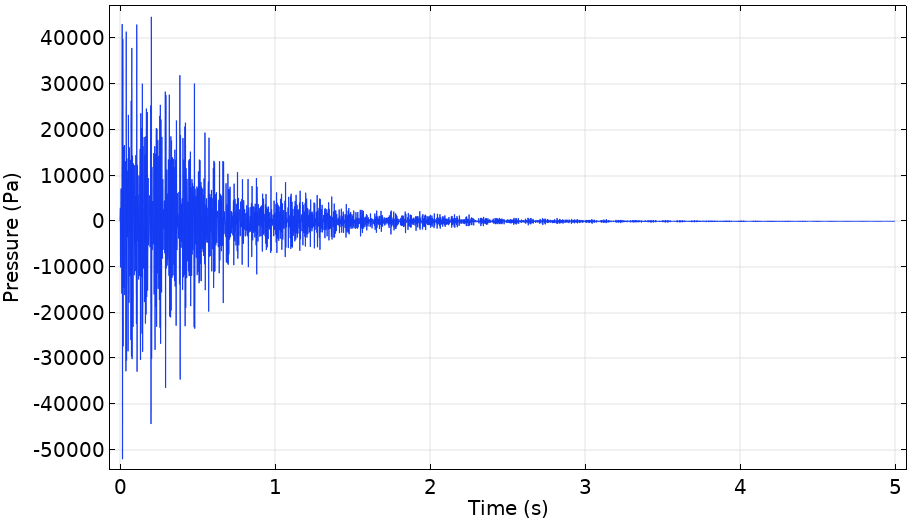
下面左图显示了 iFFT 产生的瞬时压力。正如预期的那样,原始数据的对数是有噪声的,因此使用高斯平均来平滑信号,如右图所示。内置高斯脉冲函数和 iFFT 数据的卷积积分是通过沿一维分量放置脉冲和 iFFT 数据,并使用线积分组件耦合在直线上积分(合适的被积函数)来实现的。
左图是低频下 FEM 预测的 iFFT 瞬时压力,右图的红线是瞬时压力的对数,而蓝线是红线的平滑版本。
压力的平滑对数在时间周期的中间大致呈线性。通过外推这种情况,图中显示浴室的T60 值大约为 6 s。这表明在阿基米德的浴室里谈话是困难的,但是,如果被发明出来的话,格里高利的圣歌听起来会很美妙。
为了验证我们的结果,我们可以将其与一种能够有效预测模式 T60 值的简单方法进行比较。我们将本征频率的虚部乘以 0.9 来估计模式的 T60 值。在这种情况下,iFFT 研究的中心频率为 250 Hz,最近模式为 255 Hz,该模式将主导响应,相应的 T60 值为 5.9 s。
结论和思考
在这篇博文中,我们使用了 COMSOL Multiphysics 软件和内置的声学模块在一个非常简单的封闭空间中模拟单极子和偶极子。我们证明了一个有趣的现象:当把基源放在一个封闭区域的特定位置和频率时,基本源基本上不产生声音。此外,我们还使用 了FEM 来预测低频 T60 值,而没有采用似是而非的射线近似法。
下一步
点击下面的按钮,了解声学模块中提供的声学建模专业特性。
相关资源
- 尝试用下列案例来模拟封闭空间的声学效果:
- 阅读COMSOL 用户年会2018上海站发表的论文: 工程师如何为室内声学的衰减时间创建模拟测试台。







评论 (0)