通常,我们用辐射传热方程(radiative transfer equation,RTE)来描述半透明介质中的辐射热量传递过程,但求解该方程的计算成本较大。根据介质的辐射特性,我们可以简化方程,减少计算时间。本文介绍了在 COMSOL Multiphysics 种求解辐射传递方程的 4 种方法以及何时使用这些方法。
什么是辐射传递方程
一束入射光沿 \Omega 方向在参与介质中传播并与介质发生作用。部分光强 I(\Omega) 被 \kappa I(\Omega) 部分吸收,\kappa (m^{-1}) 为吸收系数;另一部分光沿 \sigma_s I(\Omega) 方向散射,\sigma_s(m^{-1}) 为散射系数。定向传播的光强会因不同方向的散射而衰减,也会被来自不同方向的辐射所增强。因此,这一过程可以用下述方程来描述:
(1)
其中,射线从 \Omega^{\prime} 方向散射到 \Omega 方向的概率用散射相位函数 \phi(\Omega^{\prime},\Omega) 来描述。\kappa I_b 表示介质在所有方向上的辐射,其中 I_b 是黑体的强度。
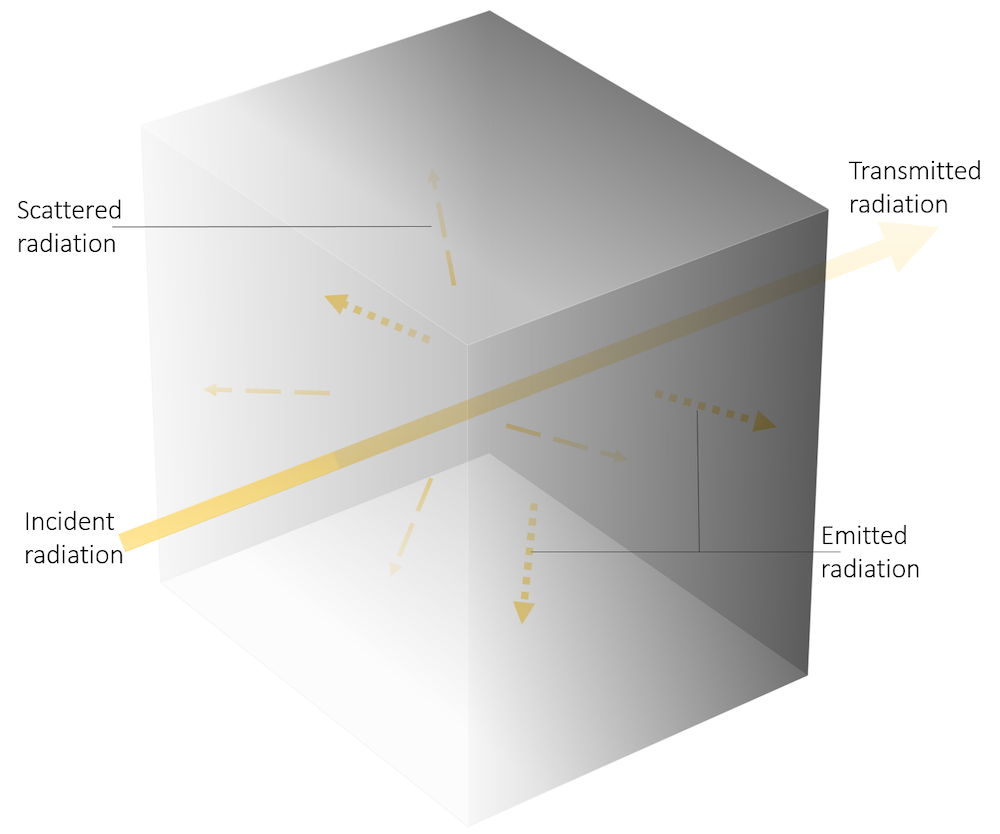
辐射与半透明介质相互作用。
所有这些影响都可以由辐射传递方程描述:
(2)
{I(\Omega^{\prime})\phi(\Omega^{\prime} ,\Omega)d\Omega^{\prime}}
散射积分的近似值是计算该方程的关键。结合热传递过程,入射辐射可以表示为:
(3)
此外,辐射热通量也很重要,可以表示为:
(4)
用光学厚度或光学深度来表示参与介质的量:
(5)
它描述了介质对辐射的透明性。如果 \tau\ll 1,将介质称为“光学较薄”,如果 \tau\gg1,则称为“光学较厚”。
4 种计算辐射传递方程的方法
下面,我们介绍 4 种在 COMSOL Multiphysics® 软件中计算辐射传递方程的方法:
- 离散坐标法(Discrete ordinates method)
- P1 近似
- Rosseland 近似
- 比尔-朗伯定律(Beer–Lambert law)
除最后一种方法外,其他 3 种方法属于天体物理学范畴。关于这些方法的详细解释与说明请参考 Modest M F (参考文献1)编著的书《辐射传热》(Radiative Heat Transfer)。
方法1:离散坐标法
计算辐射传递方程的最常用的方法是离散坐标法。该方法的原理是计算离散方向上的纵坐标分量。因此,仍然需要通过计算每个离散纵坐标上的偏微分方程来求解强度 I:
(6)
其中,\mathbf{S}_i 是第ith方向的离散纵坐标,w_j是正交的权重。
上一篇博客文章中介绍了如何将角度空间划分为离散坐标的详细方法。默认的SÑ方法使用 N 阶对称正交,并将 3D 角空间在 N(N+2) 个方向上划分。下图显示了对称偶数正交集和不同阶数的离散坐标 N。
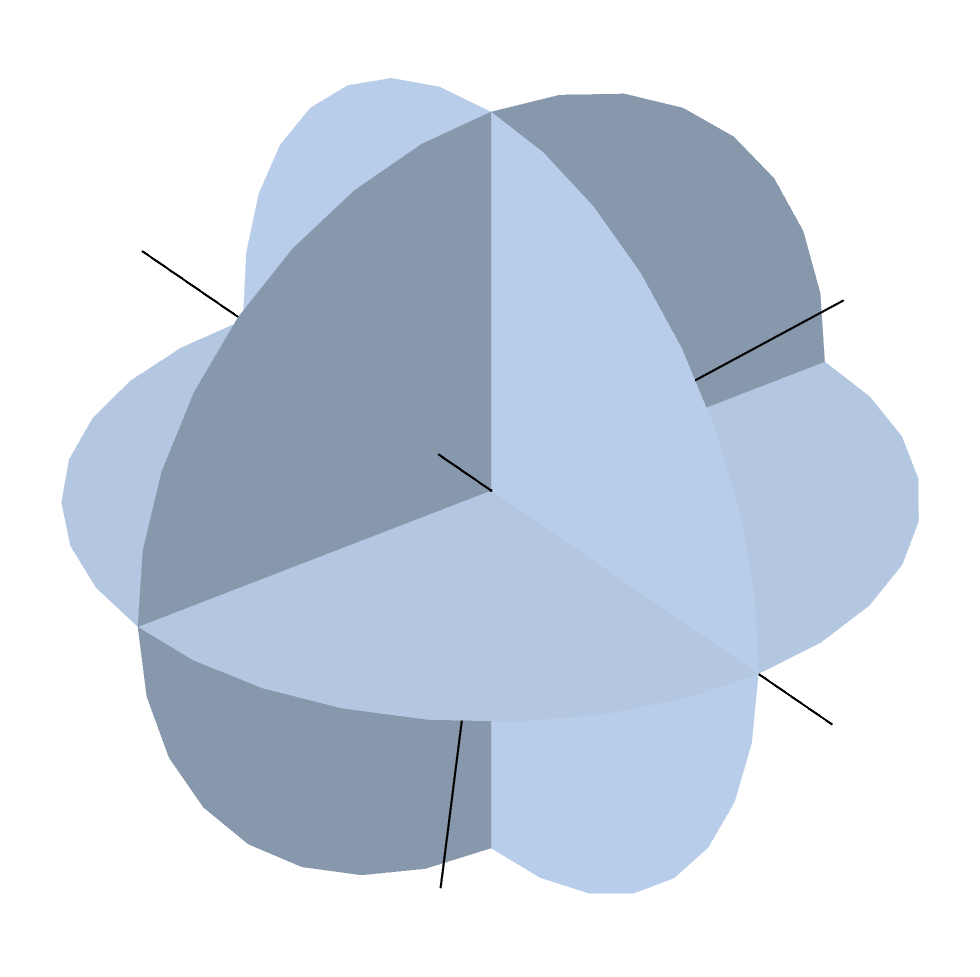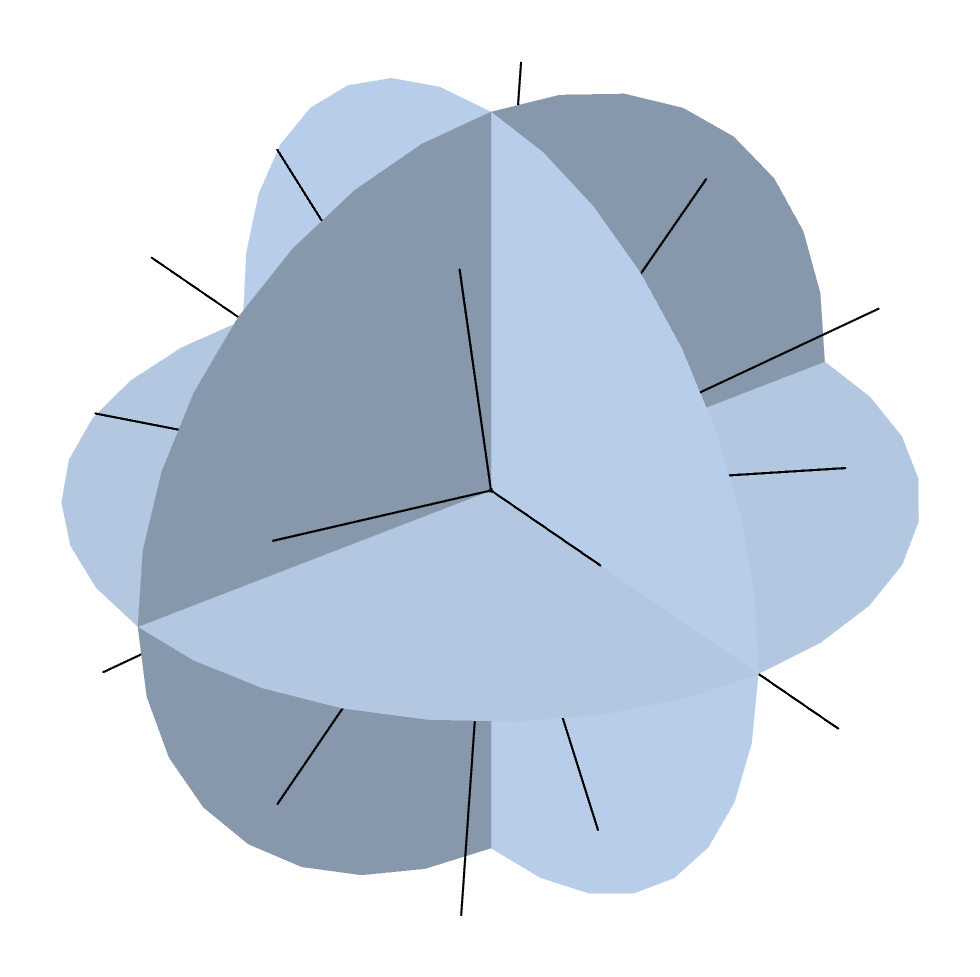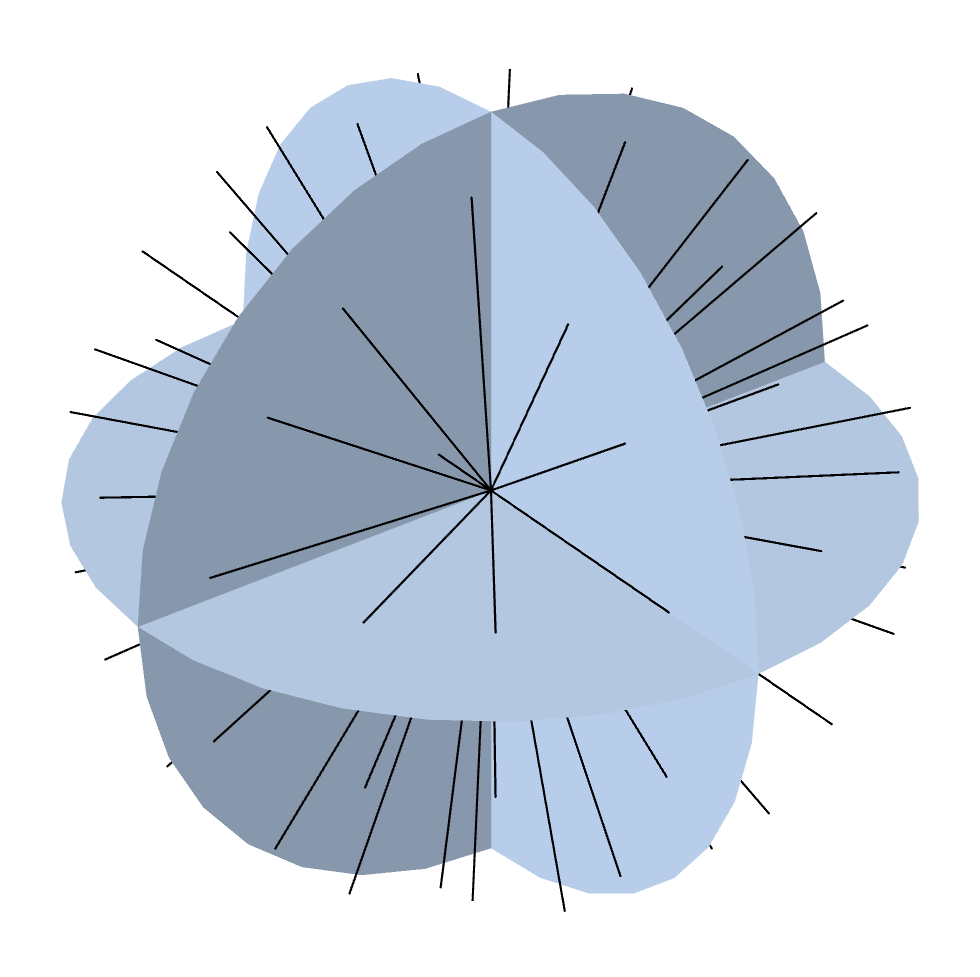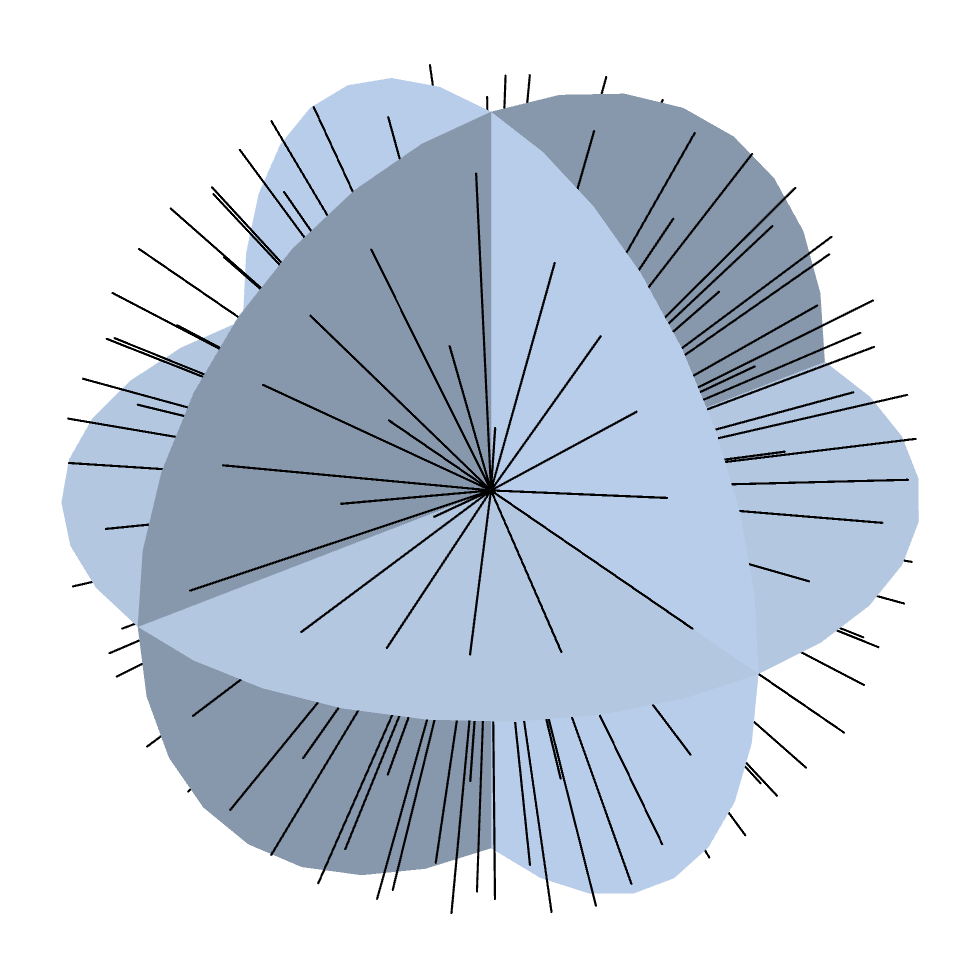
S2 到 S12(8–168 个方向)的水平对称偶数正交集的离散坐标。
对于大多数应用,默认的 S4 方法已经足够,但是已经为强度引入了 24 个因变量。相对于其他方法,离散坐标法的主要优点是,由于角空间的离散化,因此在任意配置中都具有较高的精度。另外,该方法可以处理各种形式的散射相位函数:各向同性,线性或多项式各向异性以及 Henyey-Greenstein。
由于此方法的计算比较耗时,对于复杂的 3D 几何结构,普通计算机的内存往往不够大。因此,我们简要介绍一种简单的调整求解器的方法-性能指标,该指标可用于接口。
假设我们需要非常准确的计算结果,并使用 S8 方法,该方法会在模型中添加 80 个额外方程。求解器将这些变量分为多个单独的组,并且在求解器移至下一个组之前,需要在单个迭代步骤中计算每个组。性能指标控制创建的组数。当性能指标为 0(最小值)时,将创建 10 个组,其中每个组包含 8 个强度变量。当性能指标为 1(最大值)时,则每个强度变量将进入一个单独的隔离组中,并且所需的内存仍然较低。这种方法也适用于较大的模型,但是计算时间会增加。
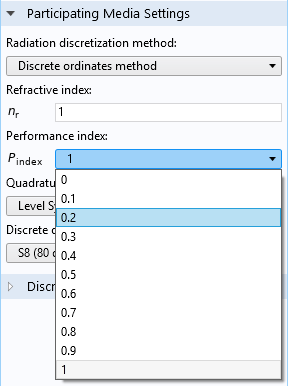
使用性能指标来控制求解器。
方法2 :P1 近似法
P1 近似法不使用离散的坐标,而是基于球面调和函数来离散角度空间。它们是拉普拉斯算子在球坐标系中的特征函数。P1 近似法仅使用了线性项,由此可得出,求解以下方程等效于求解方程式(3):
(7)
其中,
D_\textrm{P1} 是 P1 扩散系数,可以定义为:
(8)
线性勒让德系数(linear Legendre coefficient)用于散射相位函数。
因此,使用 P1 近似法,可以考虑各向同性和线性各向异性散射。等式左侧的第二项代表辐射热源 Q_\textrm{r}。因此,仅需要一个附加方程来考虑辐射传输。
方法3:Rosseland 近似法
首先,对于密度为 \rho(kg/m^3),热容为 C_p(J/(kg\cdot K)) 和导热系数为 k(W/(m\cdot K) 的介质,其静态热方程可以表述为:
(9)
式中,等式左边的第一项是对流项,右边的是热源项。
热通量 \mathbf{q} 的传热机可以用傅立叶定律表示:
(10)
回到参与介质中的辐射,在大光学深度 \tau\gg 1 的假设下,光传播的行为类似于热传导,等式(10)可以写作下式:
(11)
其中,k_\textrm{R} 是具有高度非线性的“辐射传导率”:
(12)
式中,\beta_\textrm{R}=\kappa+\sigma_\textrm{s} 是 Rosseland 平均消光系数,\sigma(W/(m^2K^4)) 是斯特藩-玻尔兹曼常数(Stefan–Boltzmann constant)。
该方法不需要增加额外的方程来计算参与介质中的辐射,仅需要增加一个高度非线性的电导率项,因此计算量较小。但是,这种近似有效的方法具有局限性,仅能求解部分应用问题。在此方法中,辐射仅与温度及其梯度有关,而不考虑其与光源的方向或距离。因此,Rosseland 近似法只适用于具有非常大的光学深度的介质。该方法最早由 Rosseland 开发,适用于恒星大气,也是玻璃工业中广泛使用的方法。
由于 Rosseland 近似法为等式(9)增加了一个附加项,因此它可以作为固体特征的扩展应用,称为光学厚参与介质。

在具有较大光学深度时,可用于考虑辐射的子节点。
方法4:比尔-朗伯定律
该方法对辐射传递方程作了最大的简化,但是如果满足以下条件,仍然可以得到精确的计算结果:
- 辐射源为单色直射光束
- 介质中的折射、反射或散射可以忽略
- 在入射光束的波长范围内没有发射
在光度测定法和化学成分分析中,就采用了这种方法计算。辐射传热方程可以简化为:
(13)
- \mathbf{e}_i 为光束的方向。
当光束穿过介质时,能量被吸收,辐射热源项可以表述为:
(14)
因此,比尔-朗伯定律描述了当光束穿过介质时,由吸收引起的辐射强度衰减。
验证示例:参与介质中的辐射
本节我们讨论几个使用上述几种方法的示例,并比较了参与介质的各种属性的结果。
冷却玻璃熔体
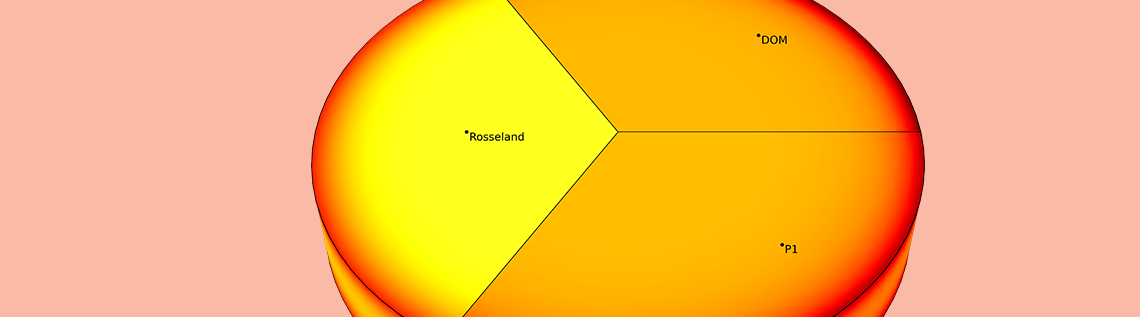
我们以一个从 600°C 冷却到 20°C 的玻璃熔体为例,来比较离散纵标法,P1 近似法和 Rosseland 近似法的典型应用。由于高温,这种冷却主要通过辐射发生。冷却 10 秒后,比较温度分布的低吸收系数和高吸收系数。
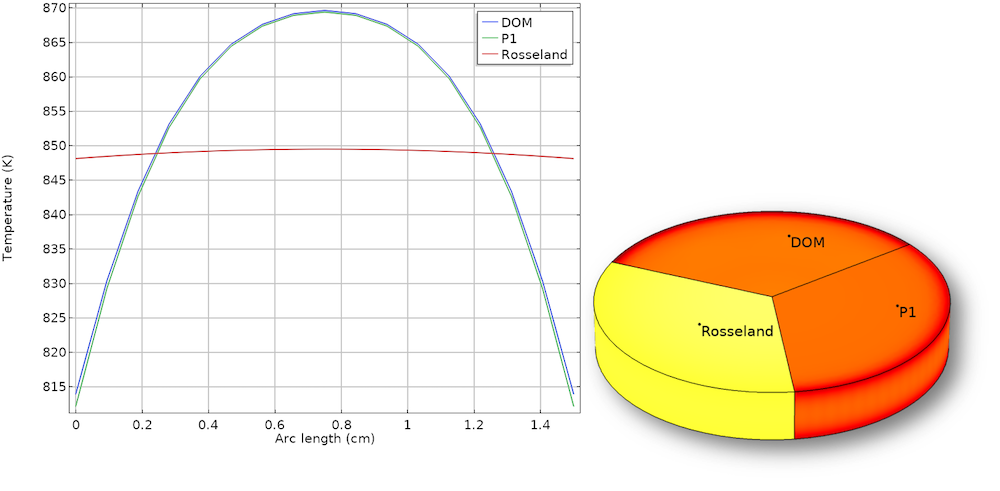
中心线和玻璃板中的温度分布 \kappa=5\ m^{-1}。对于低光学厚度玻璃板,仅使用 Rosseland 近似法是无法求解的。使用 P1 近似法可以得到精确的解。
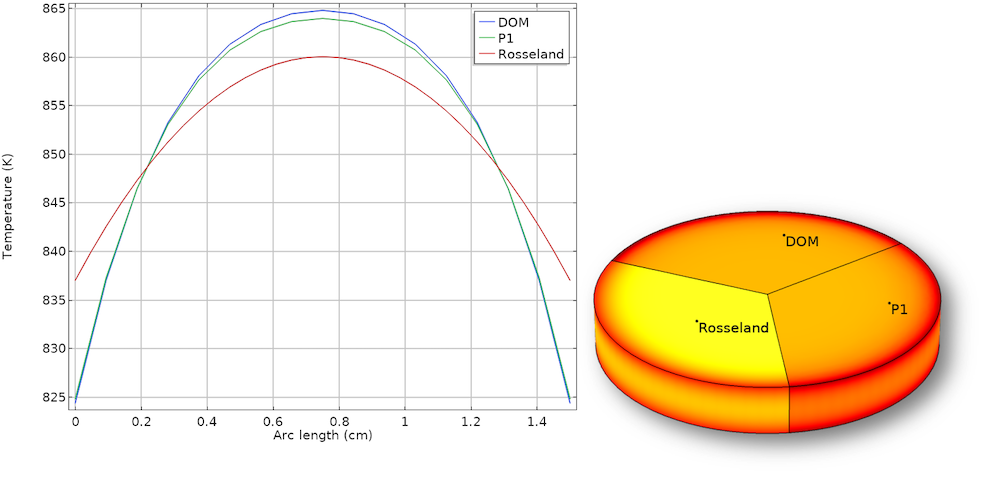
\kappa=120\ m^{-1} 时,中心线和玻璃板中的温度分布。尽管它很简单,Rosseland 逼近似法虽然计算简单,却能得到合理解。此时采用 P1 近似法仍然可以得到精确的解,但准确性低于较小 \kappa 值的情况。
此示例表明,在较大的值 \tau 范围内,P1 近似法都可以得到精确的解,并且对于光学稀薄介质也可以得到良好的结果;对于壁上存在的较小光学厚度以及较小的 \kappa 值,Rosseland 近似值具有一定的局限性;离散坐标法的计算成本明显更高,计算时间是其他方法的 10 倍。
圆柱体中的散射
为了验证 P1 近似法和离散纵标法在不同散射效果和壁特性下的准确性,研究了三种不同情况下的验证模型:
- 恒定的表面发射率,\epsilon_r=0.5,具有各向同性散射
- 径向变化的发射率,\epsilon_r=0.5(1-y/R),具有各向同性散射
- 径向变化的辐射率, \epsilon_r=0.5(1-y/R),具有线性各向异性散射
散射反照率 \omega=\sigma / (\sigma+\kappa) 用于参数化模型。
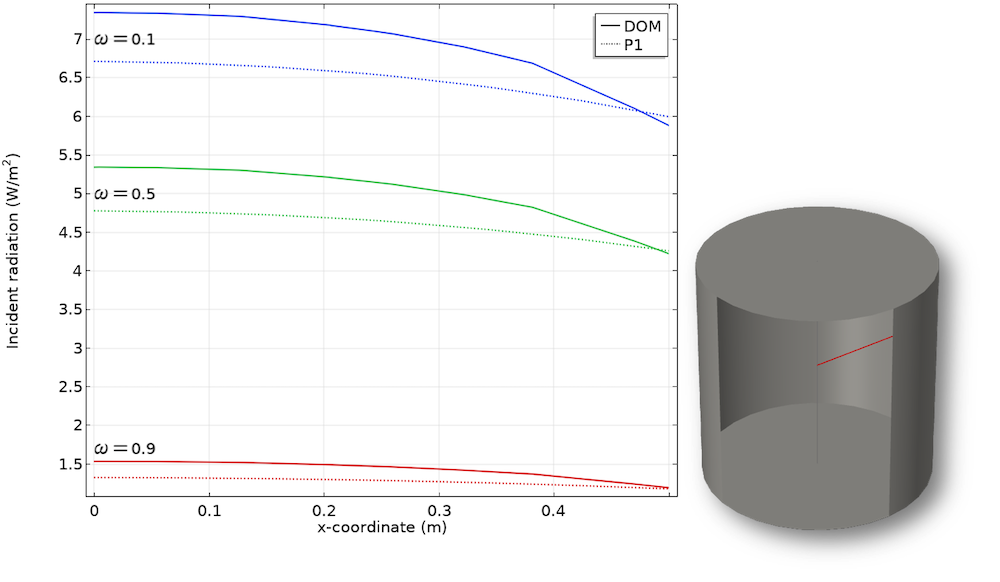
情况1:沿径向变化的各向同性散射反照率的入射辐射。
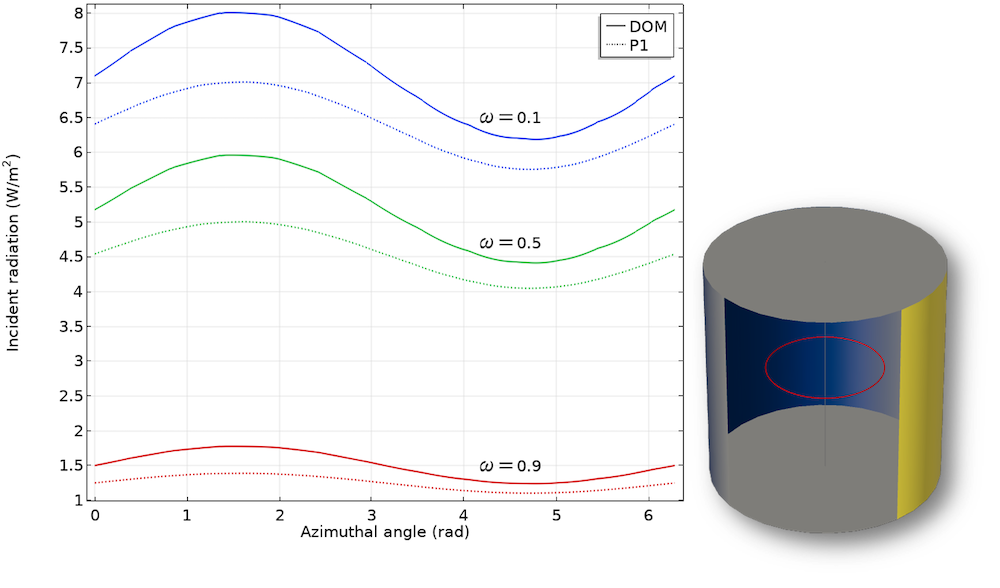
情况2:在方位角方向上各向同性散射反照率的入射辐射。
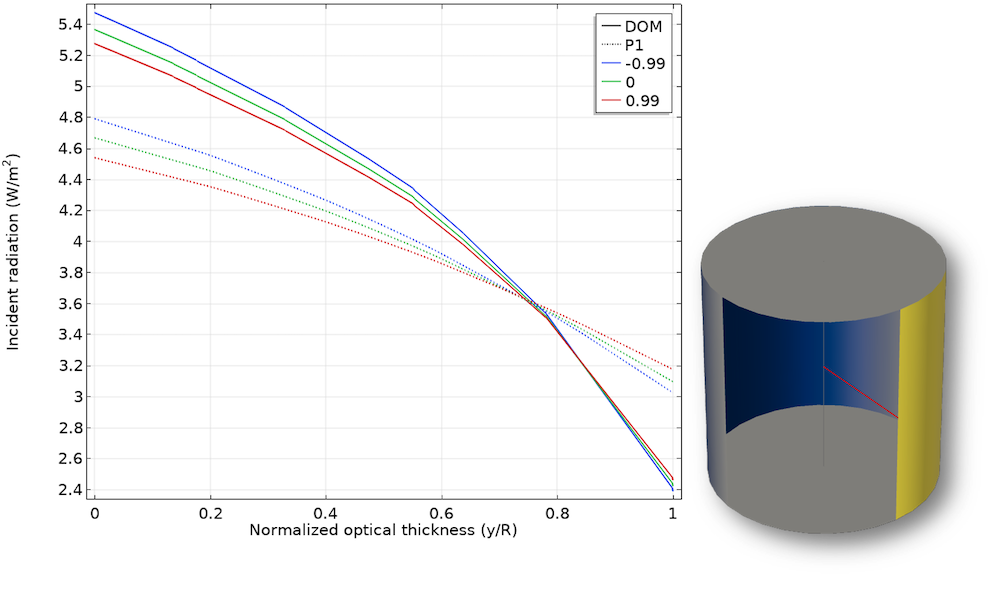
情况3:标准化光学厚度沿线性各向异性散射变化的入射辐射。
此示例表明,对于具有较大光学厚度的介质(\omega \rightarrow 1. ),采用 P1 近似可以得到比较精确的解,与采用离散坐标法的计算结果接近。对于具有较小光学厚度的介质,计算误差较大。尤其对于线性各向异性散射(情况3),该方法仅能得到近似解。尽管如此,P1 近似仍然是一个很好的近似方法,特别是当我们的计算量较小时。
结语
在本篇博文中,我们讨论的 4 种方法几乎可以计算所有参与介质中的辐射。现在将它们各自的优缺点总结如下:
- DOM
- 离散坐标法是最常用的方法,可以对离散方向(最多512个)上的所有辐射传递方程求解,计算结果精度高
- 可以包括各向异性散射的复杂形式
- 计算成本随着离散纵坐标数量的增加而增加
- P1 近似法
- 对于辐射传播的方向不占主导地位的许多配置,都可以得到精确的结果
- 只包括各向同性和线性各向异性散射方程
- 仅需要增加一个额外的标量方程,计算成本低
- Rosseland 近似法
- 适用于具有大光学深度的介质,可以得到精确的结果
- 忽略散射的影响
- 在热传递方程中使用辐射传导率,计算成本低
- 比尔-朗伯定律
- 适用于理想条件下的介质,计算结果精确
- 应用范围狭窄
- 计算成本低
其他资源
了解更多有关 COMSOL 软件中传热建模功能的信息,请单击下面的按钮。
通过查看案例教程,了解有关辐射建模的更多信息:
参考文献
- 1.M.F. Modest, Radiative Heat Transfer, Academic Press, 2003.


评论 (0)