今天我们将为您介绍 COMSOL Multiphysics® 软件中一个强大的工具——状态变量。你将学习如何用它们生成分形,例如著名的芒德布罗集合(Mandelbrot set),也就是所谓的分形噪声。生成分形不是状态变量的最典型应用。但是,这篇博客文章提供了一种有启发性、有见地并且有趣的方式,可以帮助你更多地了解如何使用状态变量、复数算法和随机数。
什么是分形?
广义上讲,分形是指物体在不同尺度上表现出某种形式的自相似性。这听起来可能很抽象,但是分形模式实际上广泛存在于自然界中——无论你是否注意过,你都可能遇到过它们。
例如,蕨类植物会显示出分形模式。下图中所示的每个蕨叶由较小的分支或细分,即所谓的 羽状叶(pinnae)组成,它们沿着主茎生长,并显示出与主叶本身相似的模式。单个羽状叶又由较小的细分(细齿)组成,在某些蕨类植物中,细齿 可细分为更小的部分。

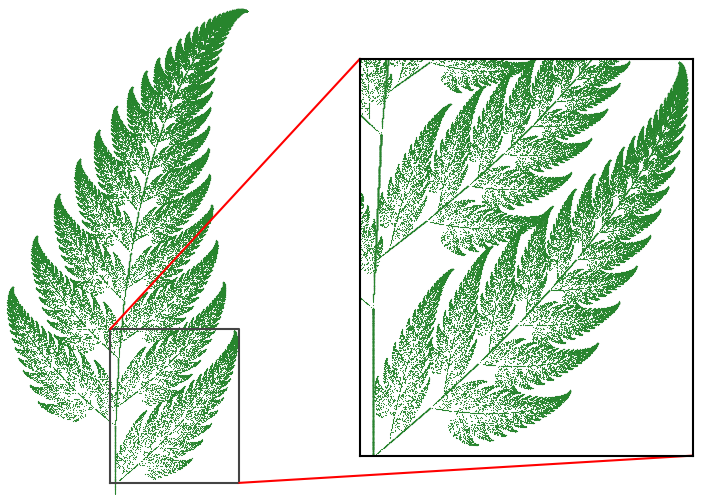
自然界真实的蕨叶和计算机合成的 Barnsley 蕨。
数学对应体的发现是受自然界中发现的植物图案启发的,即Barnsley 蕨。蕨叶的这种数学表示可以在具有迭代功能的计算机上生成,这个迭代功能只需要几行代码就能完成。生成的图像类似于蕨叶,就像真实的蕨叶一样,它由细分形状组成,这些细分形状与主叶片本身相似。实际上,Barnsley 蕨经常会无限细分为较小的自相似形状,而真实蕨类植物中的自相似性仅能保持几个水平。
分形除了具有吸引人的外观外,还具有各种实际应用,例如分形单极天线和超材料研究。另一个应用是计算机生成图像,例如在计算机游戏中模拟自然物体,像风景、云彩、树木或其他植物。在这篇博文的后面部分,我们将展示如何使用分形模式生成看起来逼真的景观图像。
芒德布罗集合
也许最著名的一个分形是芒德布罗集合。简而言之,它是由一个简单的迭代函数产生的一组复数。如果将复数插入到某个迭代函数中,且绝对值经过多次迭代后不会发散,则将其视为集合的一部分。要检查一个数是否是集合的一部分,我们只需要将它插入下面的公式中就可以了:
例如,我们可以尝试用数字 c=1+0.25 i 代入。第一次迭代产生 z_1=1+0.25 i(|| z_\textrm{n} ||=1.03),第二次迭代产生 z_2=1.94+0.75 i(|| z_\textrm{n} ||=2.08),第三次迭代产生 z_3=4.19+3.16 i(|| z_\textrm{n} ||=5.25),等等。在这种情况下,绝对值 || z_\textrm{n} || 似乎发生了发散,所以,1+0.25 i 不属于芒德布罗集合。
在 COMSOL Multiphysics® 中计算芒德布罗集合
实际上,在 COMSOL Multiphysics 中计算芒德布罗集合非常简单。为此,我们创建了一个二维几何,可以将其理解为一个复平面。每个点 (x,y) 在这个平面上代表一个复数 c=x+i y,我们可以将这些点插入迭代方程中。我们必须跟踪之前的结果 z_\textrm{n},来计算下一个数 z_\textrm{n+1} 。
对于从之前的计算步骤中跟踪数据的情况,状态变量 特征是一个方便的工具。在状态变量 特征中,我们可以根据需要定义尽可能多的变量。在计算芒德布罗集合时,我们定义了两个变量,分别是 zn 和 aura。
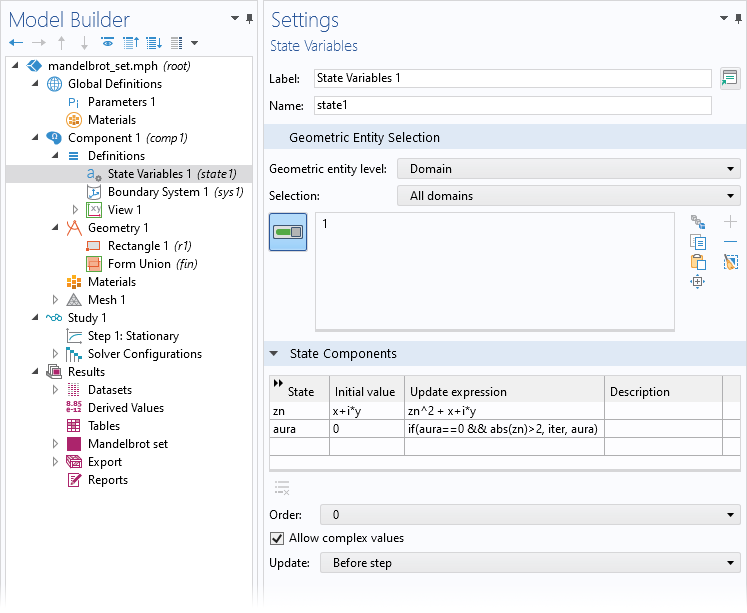
定义状态变量。
在任何给定的迭代步骤以及复平面中的任何给定点,第一个状态变量跟踪当前的值。我们在 初始值 列中对 zn 进行初始化。该更新表达式 是我们的迭代函数,通过这个函数我们将结果 zn 的平方从之前的迭代中添加到。我们还添加了另一个名为 aura 的状态变量,并将字段初始化为零,存储所需的迭代次数,直到 zn 的绝对值大于 2。
可以证明, z_\textrm{n} 最终会发散,如果 || z_\textrm{n} || > 2 在某些迭代步骤中。如果我们对这些函数进行两次迭代求解并绘制结果图,我们将看到芒德布罗集合出现,如下面动画所示。
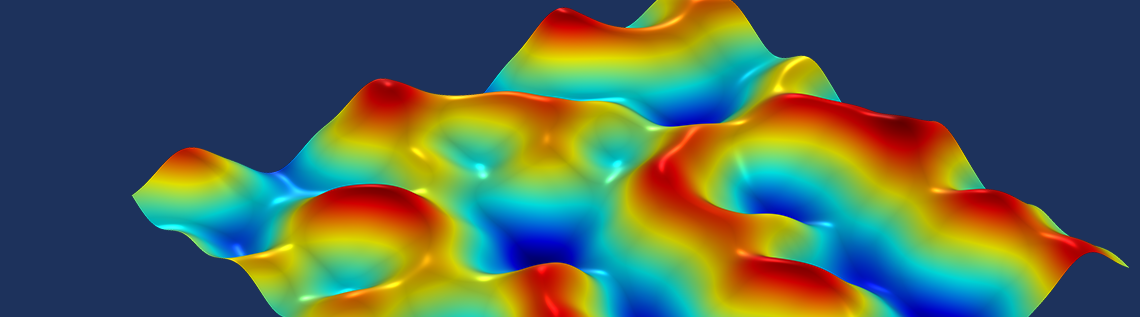
芒德布罗集合及其经过 25 次迭代计算的“光环”。
黑灰色形状代表复数,是芒德布罗集合(变量 zn)一部分。在每次迭代中,我们都更接近实际作为集合一部分的数。不同的灰色阴影表示绝对值 zn。对于一些初始值,迭代函数不会收敛到单个值,而是会在不同的值之间跳转,在动画中,它看起来有点像光源被打开和关闭。芒德布罗集合外的彩色字段表示光环,它指示发散的速度。越接近芒德布罗集合的边界,在绝对值大于2之前越需要进行多次迭代。

螺旋结构位于中心位置,使用 300 次迭代计算得出。图像的宽度为0.01,高度为0.00666。
分形噪声
现在我们已经了解了分形和状态变量的要点。接下来,我们来看看分形在计算机生成图像领域中更实际的应用。更具体地说,我们将研究如何使用所谓的分形噪声来模仿逼真的纹理。这项技术实际上已在 COMSOL Multiphysics 中用于实现各种材料的逼真可视化,这将在后面讨论。分形噪声的另一个常见应用是在计算机游戏中以程序的方式生成看起来自然的地形。
我们使用噪声创建一个人造景观。这里,我们将噪声理解为一些随机值。换句话说,我们正在寻找一个函数,即 noise(x, y),该函数以两个坐标作为参数并返回一个伪随机数。结果被解释为给定位置处的地形高度。使用 COMSOL Multiphysics 中的随机 函数,我们可以创建白噪声(详可参看这篇博客文章:从概率分布函数中抽取随机数)。如果将结果绘制在 xy 平面上,这些数将随机且独立地从一个坐标跳到下一个增量。显然,这看起来与现实世界中的任何景观都不一样,因此我们需要一种更好的方法。

白噪声分布均匀。值在一些最小值和最大值之间随机跳跃。
佩林噪声
我们正在寻找一个产生随机值的噪声函数,同时该函数不应显得“太随机”而应显得自然一些。相邻点之间应该有一些连贯性。由 Ken Perlin 开发的佩林噪声是一种特殊的噪声形式,它允许我们为给定坐标生成伪随机值,并且噪声值从一个点到相邻点的过渡是平滑的。这种“平滑的随机性”看起来更像自然界中发现的模式。
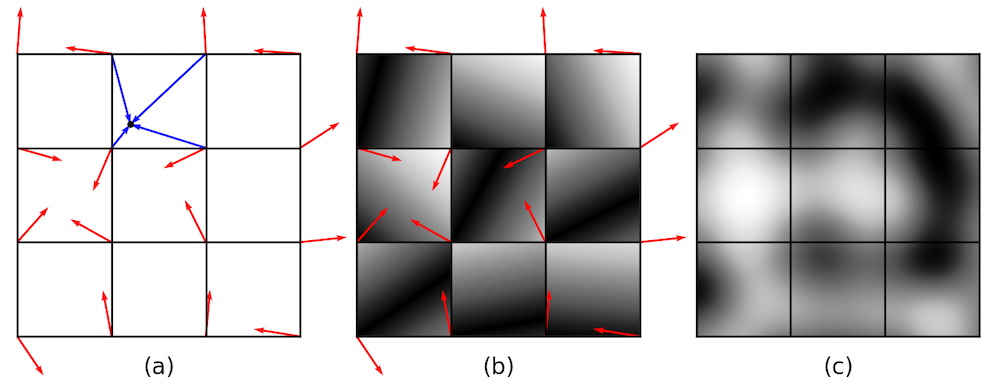
生成二维佩林噪声:(a)网格定义。红色箭头是随机生成的梯度矢量(按 0.5 缩放以更好地显示)。蓝色箭头从周围的网格指向某个位置。(b)使用左下梯度矢量的第一个点积的绝对值。灰度表示介于 0 (黑色)和 1(白色)之间的值。(c)内插噪声。
生成佩林噪声涉及上面概述的几个步骤。第一步,将 xy 平面划分为单元正方形网格点。在每个网格点处,生成一个长度为 1 的伪随机矢量,该矢量也称为梯度矢量(红色箭头)。与一个点关联的四个周围的梯度矢量 (x,y) 只是伪随机的,因为当我们在同一点重新计算噪声时,它们应该始终相同。利用梯度矢量,我们可以开始计算位于平面内任何位置的某个点的噪声值 (x,y)。对于这个给定的点,计算梯度矢量之间的四个点积,以及从网格指向所选点自身的位置矢量(x,y)(蓝色箭头)。
四个点积可以解释为梯度对所选点处的噪声水平的影响。梯度矢量 \mathbf g_\textrm{i} 以及位置矢量 \mathbf x – \mathbf x_\textrm{gi} 之间的点积,会达到最大值,当两个矢量指向同一个方向时;而当两个矢量相互垂直时会达到最小值。生成佩林噪声的最后一步是计算四个点积的加权平均值并返回插值。这涉及精巧选择的平滑步长函数和线性插值,可确保我们在自己的域上获得平滑过渡。有关如何计算佩林噪声的更多详细信息,请参见 参考文献1。
分形噪声
上面我们生成的佩林噪声具有非常平滑的过渡,并且可能看起来不像大多数现实世界中的地形那样。在该地形中,我们通常会发现更多局部不规则性,可能是来自山丘或较小的岩石。我们该怎么模拟呢?一个解决方案是叠加不同的噪声八度,这就是分形概念起作用的地方。基本上,我们会以更高的频率产生更多的噪声,换句话说,在相同的距离内会产生更多的峰谷。就像音乐中一样,频率每倍频增加一倍。降低高频噪声的幅度,并将其添加到基本噪声中。原则上,我们可以添加任意数量的噪声八度。因此,我们不再只调用一次函数 noise(),而是多次调用该函数,然后将结果与调整后的幅度相加。
如果我们将 h 解释为我们景观的高度,第一次迭代(j=0)得出具有大的、明确特征(例如山脉)的地形的第一个平滑近似值;第二次迭代可能来自更多的当地丘陵和洼地;第三次迭代可能来自单个巨石和岩层;等等。
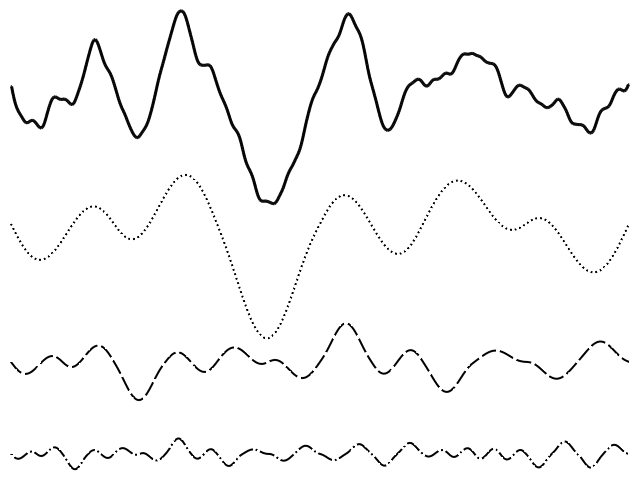
一维分形噪声(顶线)。以下是佩林噪声的前三个频率,这些频率加在一起后,就形成了顶部的线。
产生分形噪声涉及计算和叠加不同频率的噪声。在 COMSOL Multiphysics 中进行此操作时,再次方便地使用状态变量,因为我们要“记住”以前所有频率的合成噪声。以下动画表示二维高度图,其中,随着每个级别的高频噪声的出现,地形中越来越多的细节出现,该噪声被添加到基本噪声中。
我们可以在物理模拟环境中使用随机化的表面几何形状,例如,需要模拟表面粗糙度或不均匀的材料。在之前的博客文章中,我们展示了一种通过叠加具有变化幅度和频率的三角函数来创建随机表面几何形状的不同方法,以及从图像或文本文件创建任意几何形状的方法。
通过使用噪声改善材料外观
你是否知道我们还可以在绘图中添加分形噪声来改善 COMSOL Multiphysics 中的材质外观?从 5.6 版本开始,材料具有特殊的可视化选项。某些内置材料类型,例如生锈的钢、皮革和水,会使用单纯噪声创建更逼真的纹理。单纯噪声与佩林噪声相似,并且也由 Ken Perlin 开发。你可以自己调整噪声参数以获得所需的效果。
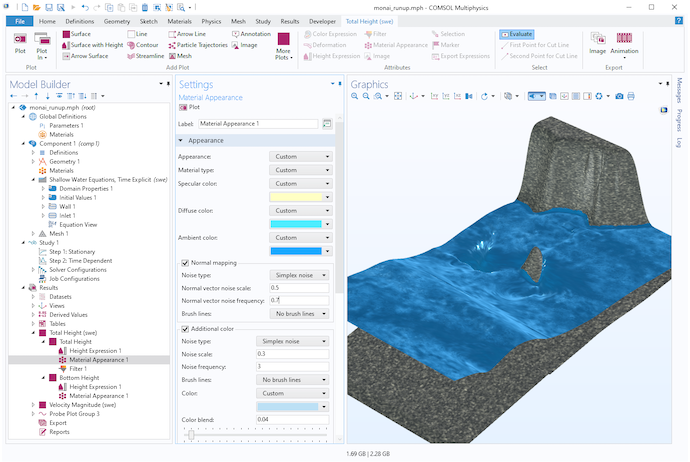
海啸冲上莫奈山谷海滩的复杂三维模型中利用单纯噪声可视化水。
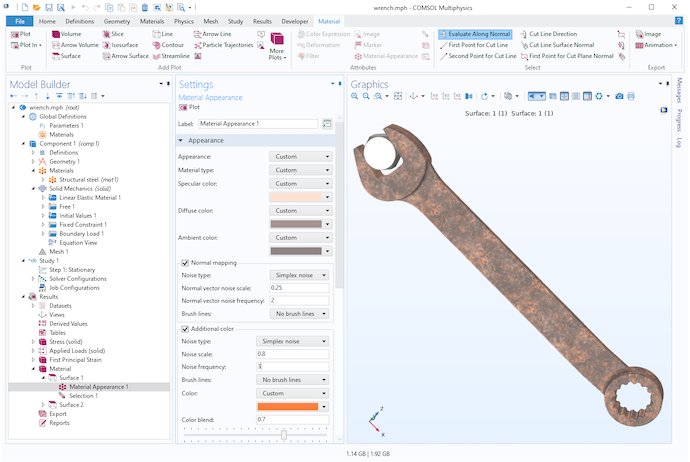
使用 Simplex 噪声可视化具有生锈钢表面的扳手的应力和应变模型。
自己尝试
想不想自己尝试模拟文中讨论的芒德布罗集合或佩林噪声?单击下面的按钮访问MPH文件,就可以动手操作了~
参考文献
- K. Perlin, “Improving Noise”, New York University, 2002. https://mrl.cs.nyu.edu/~perlin/paper445.pdf.
扩展阅读
阅读下面相关博客文章,了解有关分形、噪声和状态变量的更多信息:






评论 (0)